基于改进的强跟踪滤波GPS校频系统误差处理方法

杨少尘，胡昌华，李红增，周志杰，杜党波

（火箭军工程大学控制工程系，陕西　西安 710025）

基于改进的强跟踪滤波GPS校频系统误差处理方法

杨少尘，胡昌华，李红增，周志杰，杜党波

（火箭军工程大学控制工程系，陕西西安 710025）

GPS信号校准晶振信号频率源系统可输出高准确度时频信号，但GPS信号在传输和接收过程中会产生随机抖动或野值，给系统频率校准带来误差。为减小GPS信号随机抖动和野值所带来的影响，根据GPS信号与晶振信号准确度互补的特点，建立GPS信号校准晶振信号频差模型，利用强跟踪滤波算法对频差信号误差进行修正。针对GPS信号中存在的野值问题，对强跟踪滤波算法进行改进，根据残差变化率的大小判别野值，利用替代法对野值加以修正，提高滤波准确度。将该方法应用于某GPS信号校准晶振信号频率源系统，可使系统输出频率准确度达到10-11量级。

GPS校频；晶振；强跟踪滤波；野值

0　引言

随着计算机与信息技术的迅猛发展，许多领域都需要高准确度时间频率基准源作为参考。目前在高准确度频率源中，氢钟、铯钟的频率准确度可达10-12～10-15量级，长期稳定性好，但价格昂贵，使用条件苛刻；高稳定性晶振的频率准确度一般为10-7～10-9量级，短期稳定性好，价格低廉，但其准确度易受温度、老化等因素影响，长期稳定性较差。

GPS卫星上所携带的原子钟使GPS信号具有原子频标的长期稳定性和频率准确度。利用GPS信号校准晶振信号可获得长期与短期稳定性都很好的频率源，性价比高，实用性强［1-2］。但GPS信号在传输与接收过程中容易受到各种噪声干扰而产生一定的抖动，甚至会引入较大的野值，如果不进行处理直接作为基准信号来校准晶振，系统的频率准确度只能达到10-9量级。

目前，国内对于GPS校频系统的误差处理问题已提出了一些解决方法，但大多数只研究了GPS信号的随机抖动问题，对剔除野值的研究较少涉及。文献［3］提出利用Kalman滤波算法克服卫星信号抖动及测量噪声的方法，但其没有考虑晶振频率漂移的影响；文献［4］提出采用多次采样取平均值的方法对频差数据进行平滑处理，该方法易于实现，但不适用于实时处理；文献［5］提出通过建立GPS信号与晶振信号的频差模型，利用最小二乘法估计晶振频率漂移系数，但该方法所需样本数据多，计算较为复杂，且没有考虑GPS信号的野值对系统准确度的影响；文献［6］提出采用基于M估计的Kalman滤波算法，首先判别频差信号是否为野值，然后对滤波信息进行修正，但当信号测量值变化率较大时容易被误判为野值，会对滤波精度造成较大影响。

针对上述问题，本文提出一种基于改进的强跟踪滤波［7］的GPS校频系统误差处理方法，建立GPS信号校准晶振信号频差模型［5］，利用强跟踪滤波算法对频差信号误差进行实时修正，以弥补Kalman滤波鲁棒性差的缺陷［8］。为消除信号中野值的影响，对强跟踪滤波算法进行一定的改进，利用残差变化率判别检验野值，并采用替代法对野值加以修正［9］，在剔除野值的同时，能够保留因变化率较大而容易被判为野值的测量值，提高了滤波的准确度，从而确保系统能够保持高频率准确度输出。

1　问题描述

GPS信号校准晶振信号频率源系统基本原理如图1所示。GPS接收模块将GPS信号进行解码处理，输出1pps信号，然后系统将其与晶振分频所得的1Hz信号进行比对，获得相对频差，再通过D/A转换模块得到控制电压，作用于晶振以调节振荡频率，直至晶振频率准确度锁定在GPS频率准确度上［10］。

GPS信号与国际标准时之间存在误差ε，一般服从正态分布［11］

图1　GPS信号校准晶振信号频率源系统基本原理

对于不同类型GPS接收机的σ数值不同，如GARMIN型为1μs，Motorola VPONCORE型为50ns。设国际标准时序列为K∶1，2，…，k，…，其中k∈N。设GPS信号序列为Y，则有：

式中：yk——第k个GPS信号；

εk——k时刻GPS信号的随机误差。

在上述频率源系统中，恒温晶振信号包含随机误差和频率漂移误差，其中频率漂移误差为主要因素。晶振信号随机误差与GPS信号随机抖动误差相比很小，因此仅考虑晶振频率漂移误差，其随机误差可忽略不计。设晶振分频信号时间序列为Y′，由于晶振频率漂移特性近似于线性，则有：

式中：a——初始时刻晶振分频信号与国际标准时之间的偏差；

b——晶振频率漂移系数；

yk′——第k个晶振分频信号。

则晶振分频信号的偏差μ可表示为

由式（2）和式（3）可得晶振分频信号与GPS信号的频差信号序列X′：

由式（5）可知，GPS信号随机误差ε和晶振信号偏差μ会导致频差序列X′存在噪声误差。为实现系统高频率准确度输出，需要滤除X′中的ε与μ噪声误差，得到频差序列X′的最优估计值。同时，还需要对频差序列中出现的野值进行处理。

2　基于改进的强跟踪滤波的GPS校频系统误差处理方法

2.1强跟踪滤波算法

强跟踪滤波算法是Kalman滤波算法的一种改进。Kalman滤波的实质是根据系统的动态模型和观测模型，利用不断加入的观测值，期望得到系统的状态估计［12］。在此基础上，强跟踪滤波加入了可自适应求取最佳的渐消因子，提高了算法的鲁棒性和估计准确度［13］。频差信号误差处理问题运用强跟踪滤波算法解决，具有独特的优势。

在上节所述GPS校频系统中，由式（5）推导可得系统的状态方程和观测方程：

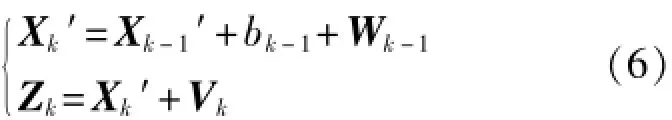
其中，k=1，2，3，…，一维状态向量Xk′为k时刻的频差信号真值；观测向量Zk为包含噪声的观测值；Wk为系统噪声，Vk为观测噪声，两者均具有零均值，其协方差分别为Qk、Rk。

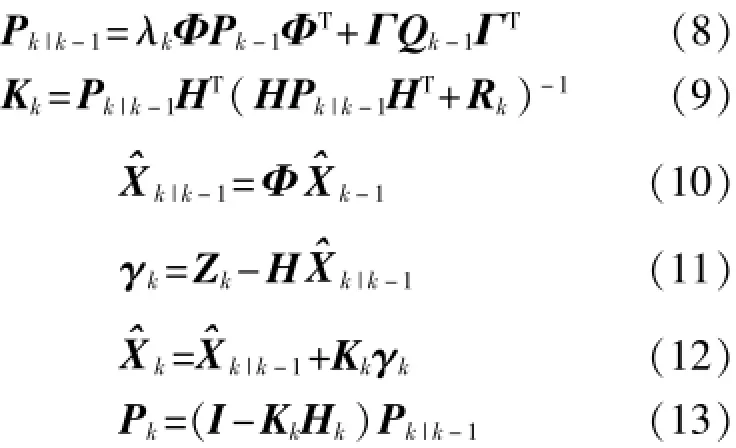
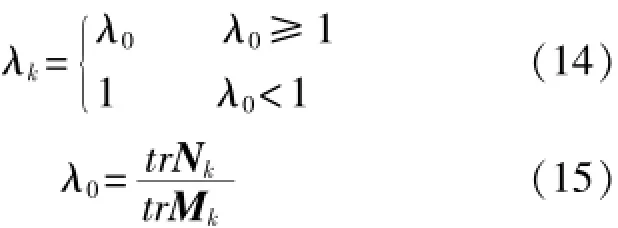
系统初始化时需给定频差信号初值X0和估计误差协方差初值P0，其值可由式（19）、式（20）计算得出：

系统噪声协方差Qk可按令滤波效果最优的原则由实验确定；观测噪声协方差可取Rk=1。

2.2自适应抗野值方法

GPS信号在传输和接收过程中所产生的较大野值会严重影响滤波算法的估计准确度。因此，在利用强跟踪滤波算法消除噪声的同时，还需对频差信号中存在的野值进行处理。

目前常用的抗野值方法有：根据滤波新息序列正交性，将活化函数加权于新息序列［14］的方法，以及基于M估计Kalman滤波的方法等。但上述两种方法都为折中方法，当测量值变化率较大时，容易被误判为野值，影响滤波准确度。为克服上述问题，本文对强跟踪滤波算法进行了一定的改进，即在强跟踪滤波算法中加入自适应抗野值方法，对野值进行处理。

将式（11）和式（23）代入式（22），可得测量值的估计：

其中，Zk+1为待判别的测量向量；Dk+1为预估的测量向量；δ为摄动向量，其取值可根据系统的准确度要求确定。则野值的判别可叙述成假设检验问题：

对于后混合式磨料射流技术仍存在一些问题。后混合磨料系统在加工精度、加工效率、加工能力等方面有待提高;对于后混合式磨料射流的流变特性、流场特性和本构方程等各项研究较少,对后混合式磨料射流流过喷嘴、射流与磨料混合、磨料加速、射流与大气的相互干扰、磨料颗粒冲击对材料的侵蚀和喷嘴移动速度对材料的体积去除率等也研究的较少。

当H0成立时，说明测量值中不存在野值；当H1成立时，说明测量值中存在野值。利用替代法，令Zk+1=Dk+1，以消除野值的影响。

综上所述，GPS校频系统频差信号误差处理问题可按如下步骤解决：

1）根据GPS信号随机误差和晶振分频信号频率漂移误差的函数分布特点，建立GPS信号校准晶振信号频差模型。

2）由频差模型推导系统的状态方程与观测方程，对系统状态和参数进行联合估计。

3）利用改进的强跟踪滤波算法对包含噪声误差和野值的频差信号进行修正。

4）将处理后的频差信号输入D/A转换模块，获得控制电压并调节晶振输出频率，实现系统的高频率准确度输出。

3　实例验证

针对某GPS信号校准晶振信号频率源系统，设定测量连续两次频差信号的时间间隔为10s。在未经过滤波处理的情况下，收集一组包含噪声干扰的频差信号序列，其平均频率准确度约为9.6140×10-9，如图2所示。

图2　含有噪声干扰的频差信号序列

由图可以看出，未经过滤波处理的频差信号序列随机抖动较大，抖动范围在±74.324 8×10-9之间，并且包含野值。因此需要对该序列的噪声和野值问题进行处理。

利用状态和参数联合估计的Kalman滤波算法处理含有噪声干扰的频差信号序列，结果如图3所示。

图3　Kalman滤波算法处理后的频差信号序列

可以看出，利用Kalman滤波算法处理频差信号序列，有一定的抑制噪声干扰的效果。但处理后序列的抖动范围仅可达到±37.9031×10-9，其信号跟踪和抗野值的能力还需进一步加强。

利用状态和参数联合估计的强跟踪滤波算法处理含有噪声干扰的频差信号序列，结果如图4所示。

可以看出，利用强跟踪滤波算法处理频差信号序列，可使其抖动范围减小至±28.7738×10-9之间，能够有效抑制噪声的干扰，说明将强跟踪滤波算法应用于该频率源系统频差信号误差的处理是合适且有效的。但处理后的曲线仍存在明显的波动，主要原因为原始序列存在野值，说明该算法具有一定的消除噪声的能力，但还需进一步改进以提高其抗野值的能力。

在强跟踪滤波算法中加入自适应抗野值方法，处理含有噪声干扰的频差信号序列，结果如图5所示。

图4　强跟踪滤波算法处理后的频差信号序列

图5　改进的强跟踪滤波算法处理后的频差信号序列

可以看出，改进的强跟踪滤波算法可使频差信号序列的抖动范围减小至±18.5326×10-9，有效抑制了野值的干扰，使滤波输出逐渐趋向于频差信号的真实值。

分别计算经Kalman滤波算法、强跟踪滤波算法和改进的强跟踪滤波算法处理后的频差信号序列均方差，结果如表1所示。

表1　经算法处理后的序列的均方差

可以看出，经改进的强跟踪滤波算法处理的频差信号序列均方差明显小于另外两种算法，说明该算法能够较好的减小频差信号中的随机噪声和野值。利用该算法处理频差信号，实时调节晶振输出频率，可确保该GPS信号校准晶振信号频率源系统的输出频率准确度达到10-11量级。

4　结束语

本文研究了一种基于改进的强跟踪滤波的GPS校频系统误差处理方法。首先建立了GPS信号校准晶振信号频差模型，利用强跟踪滤波算法对频差信号误差进行修正，并在强跟踪滤波算法中加入自适应抗野值方法，根据残差变化率的大小判别野值，利用替代法对野值加以修正，有效减小了频差信号中的随机噪声和野值的影响。将该方法应用于某GPS信号校准晶振信号频率源系统，能够满足系统输出频率准确度的要求。

［1］SANLEM D，DRISCOLL O C，LACHAPELLE G.Metho dologyforcomparingtwocarrierphasetracking techniques［J］.GPS Solutions，2012，16（2）：197-207.

［2］HAN H Z，WANG J，WANG J，et al.Reliable partial ambiguity resolution for single-frequency GPS/BDS and INS integration［J］.GPS Solutions，2016，20（14）：1-14.

［3］倪媛媛，胡永辉，何在民.北斗卫星校准铷钟单元的设计与实现［J］.测试技术学报，2011，15（2）：56-59.

［4］党晓圆，单庆晓，肖昌炎，等.基于GPS与北斗双模授时的压控晶振校频系统的研究与设计 ［J］.计算机测量与控制，2009，17（11）：2246-2248.

［5］曾祥君，尹项根，LI K K，等.GPS时钟在线监测与修正方法［J］.中国电机工程学报，2002，22（12）：41-46.

［6］宁玉磊，胡昌华，李红增，等.基于M估计卡尔曼滤波的GPS校频系统频差处理方法研究［J］.电光与控制，2015，22（12）：72-75.

［7］孙国强，黄蔓云，卫志农，等.基于无迹变换强跟踪滤波的发电机动态状态估计［J］.中国电机工程学报，2016，36（3）：615-623.

［8］ CHEN X Y，SHEN C，ZHANG W B，et al.Novel hybridofstrongtrackingKalmanfilterandwavelet neuralnetworkforGPS/INSduringGPSoutages［J］. Measurement，2013，46（10）：3847-3854.

［9］张帆，卢峥.自适应抗野值Kalman滤波［J］.电机与控制学报，2007，11（2）：188-190.

［10］SONGJ，ANQ，LIU S B.A high-resolution time to digital converter implemented in field programmable gate arrays［J］.IEEE Trans on Nuclear Science，2006，53（1）：236-241.

［11］MOSAVI M R.Use of accurate GPS timing based on radialbasisprobabilisticneuralnetworkinelectric systems［C］∥International Conference on Electrical and Control Engineering，2010：2572-2575.

［12］杜党波，张伟，胡昌华，等.含缺失数据的小波-卡尔曼滤波故障预测方法［J］.自动化学报，2014，40（10）：2115-2125.

［13］钱华明，葛磊，黄蔚.一种改进的强跟踪滤波算法［J］.应用科学学报，2015，33（1）：32-40.

［14］冯鹏程，胡高歌，高社生.基于新息正交原理的抗差UKF及其在INS/GPS组合导航中的应用［J］.测控技术，2015，34 （10）：92-95.

（编辑：李刚）

Method for error correcting of frequency source calibrated by GPS based on improved strong tracking filter

YANG Shaochen，HU Changhua，LI Hongzeng，ZHOU Zhijie，DU Dangbo
（Dept of Control Engineering，Rocket Force University of Engineering，Xi'an 710025，China）

GPS-signal calibrating crystal oscillator frequency source can output high-precision frequency signal.However，errors appear in the system because of the influence of random jitter and outliers effecting to GSP-signals in the transmitting and receiving process.To decrease the effect of random jitter and outliers，according to the complementarities between GPS-signal and crystal oscillator，a frequency difference model for GPS-signal calibrating crystal oscillator is proposed，applying strong tracking filter algorithm to correct errors of frequency difference signal. In order to solve the outliers problem，improving the strong tracking filter and according to the variety of residual difference，outliers can be corrected with substitution method，which can improve the precision of strong tracking filter algorithm.Applying the proposed method to a GPS-signal calibrating crystal oscillator frequency source，the result shows that the system can output a high-precision frequency of 10-11through the improved strong tracking filter algorithm.

GPS calibrating frequency；crystal oscillator；strong tracking filter；outliers

A

1674-5124（2016）08-0013-04

10.11857/j.issn.1674-5124.2016.08.003

2016-04-12；

2016-05-27

国家杰出青年基金项目（61025014）

国家自然科学基金项目（61573365）

杨少尘（1991-），男，北京市人，硕士研究生，专业方向为故障诊断与预测。