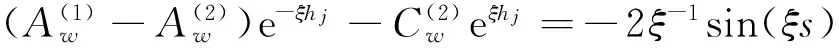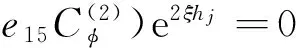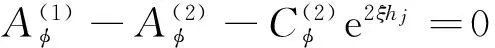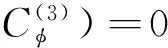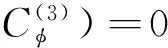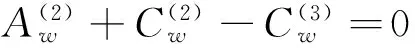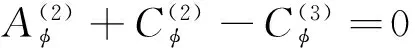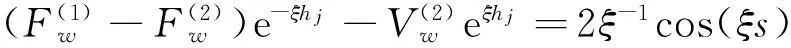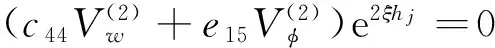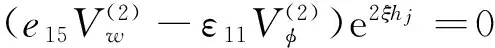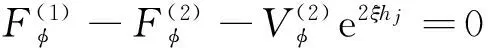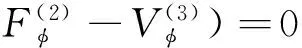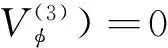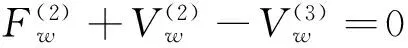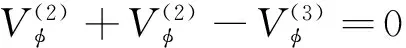铁电陶瓷平行裂纹的相互作用规律
2016-09-13卢士勇李永东
周 凯, 卢士勇, 李永东
(1. 装甲兵工程学院机械工程系, 北京 100072; 2. 中国人民解放军驻618厂军事代表室, 北京 100072)
铁电陶瓷平行裂纹的相互作用规律
周凯1, 卢士勇2, 李永东1
(1. 装甲兵工程学院机械工程系, 北京 100072; 2. 中国人民解放军驻618厂军事代表室, 北京 100072)
针对沿z轴极化的BaTiO3铁电陶瓷在xoy平面内发生平行开裂的问题,建立了断裂力学理论模型。综合运用积分变换法、位错模拟法和格林函数法,推导了该裂纹问题的Cauchy型奇异积分方程组,并采用配点法将其转化为代数方程组。通过对代数方程组进行数值求解,得到了裂纹尖端应力场的强度因子。以2条平行裂纹为例,基于数值计算结果进行了参数分析,讨论了它们的纵向间距与横向间距对应力强度因子的影响规律,并定量揭示了平行裂纹相互“屏蔽”和“干涉”的基本现象,为铁电陶瓷结构的防断裂优化设计提供了理论参考。
铁电陶瓷; 平行裂纹; 屏蔽效应; 干涉效应
铁电材料由于其优越的力电耦合性能而在智能控制与测试、信息传输与存储等领域具有广泛的应用[1]。目前,工程中常见的铁电材料是人工铁电陶瓷。由于陶瓷具有天然的脆性,因此铁电器件在制造和应用中常遇到开裂的问题,开裂失效甚至被工程界认为是制约该类智能器件性能提升的一大瓶颈。因此,断裂力学建模与分析是铁电器件设计、优化和评估中必须开展的一项基础性研究工作,也是近年来国内外断裂力学领域研究的一大热点。实际中,铁电陶瓷在外载荷作用下可能同时产生多处开裂,多条裂纹往往具有多种不同的排列形式和相互作用规律,这使得铁电陶瓷的断裂行为可能会变得非常复杂,因此,在铁电陶瓷防断裂优化设计中十分有必要研究多裂纹的影响[2]。平行多裂纹的几何构型相对简单且在理论分析方面具有较强可行性,它是构造和研究更复杂的多裂纹问题的基础。针对铁电陶瓷中的平行多裂纹问题,笔者综合运用积分变换法、位错模拟法和格林函数法,推导其奇异积分方程组,并采用配点法进行数值求解,基于应力强度因子(Stress Intensity Factor,SIF)的数值计算结果进行参数分析,同时在理论数据的基础上,用平行裂纹之间的“屏蔽”和“干涉”现象解释其相互作用规律,对铁电陶瓷结构优化和设计具有非常重要的工程意义。
1 理论模型
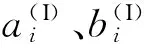
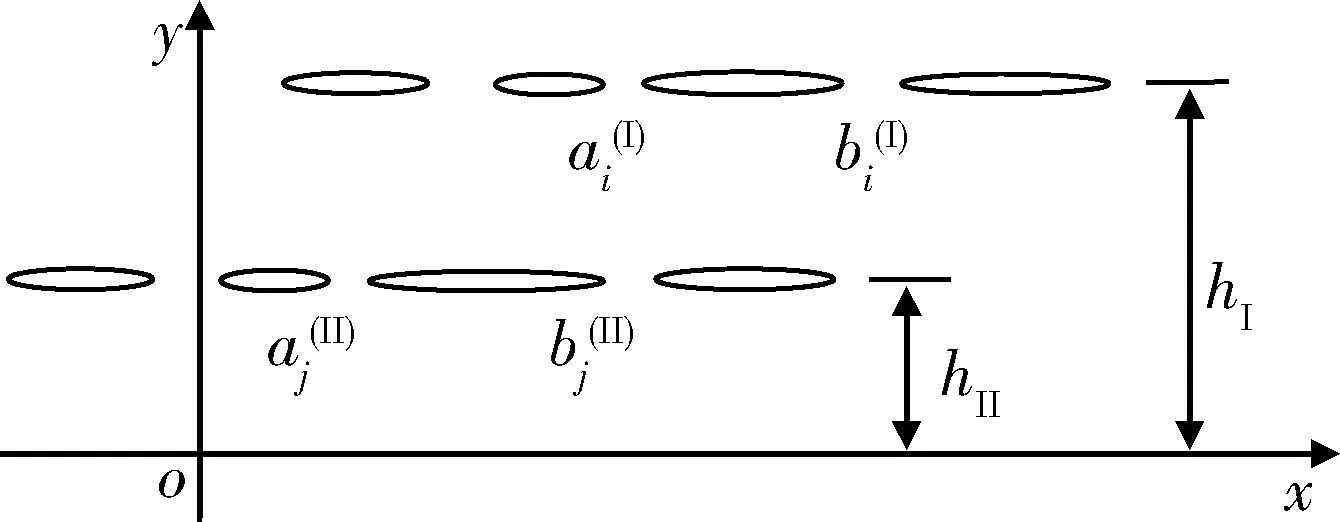
图1 铁电陶瓷中的2组平行裂纹
假设图1中的铁电陶瓷沿z轴极化,则依据压电理论[3]可知:其在xoy平面内具有各向同性性质(即横观各向同性)。假设裂纹受到反平面等效剪切载荷作用,则在xoy平面内只有反平面变形与面内电场发生耦合。在上述假设条件下,铁电陶瓷的力学、电学基本方程可表示为
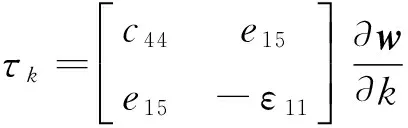
(1)
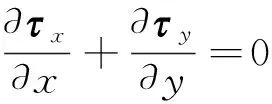
(2)
式中:k=x,y;w=(w,φ)T,为广义位移,其中w和φ分别为机械位移和电势;τk=(τkz,Dk)T,为广义应力,其中τkz和Dk分别为剪切应力和电位移;c44、e15和ε11分别为剪切模量、压电系数和介电系数。
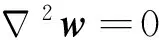
(3)
在断裂力学分析中,一般认为反平面裂纹是闭合的[2],也就是说,电势和法向电位移在裂纹上表面和下表面之间满足连续条件[4]。于是,上述裂纹问题的定解条件表示如下:
w(x,±∞)=0;
(4)
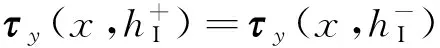
(5)
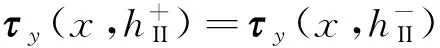
(6)
τy(x,0+)=τy(x,0-);
(7)
w(x,0+)=w(x,0-);
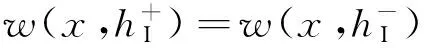
(8)
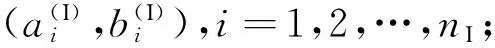
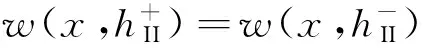
(9)
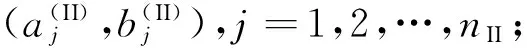
τyz(x,hI)=-τ0,
(10)
τyz(x,hII)=-τ0,
(11)
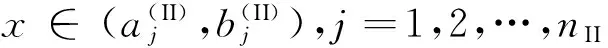
(12)
式中:-τ0为裂纹所受的反平面等效剪切载荷。
2 断裂力学分析
2.1Green函数的求解
对于图1的2组平行裂纹,本文采用位错模拟法开展断裂力学分析。将这2组裂纹用连续分布位错进行模拟,相应的位错分布密度函数[4]分别为
(13)
(14)
式中:i=1,2,…,nI;j=1,2,…,nII。
显然,式(13)、(14)分别使式(9)、(10)中的连续条件得到了满足。根据断裂力学位错理论,为使位移场满足单值性要求,式(13)、(14)在相应裂纹区间范围内的定积分需取0,即
(15)
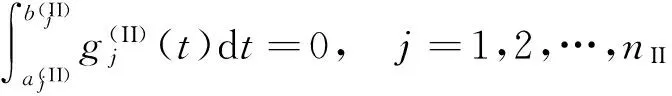
(16)
为求解连续分布位错问题,一般需先确定位错点源的响应。为此,暂时将裂纹从模型中去除,而在它们所在位置处分别引入位错点源I和II[2]:
(17)
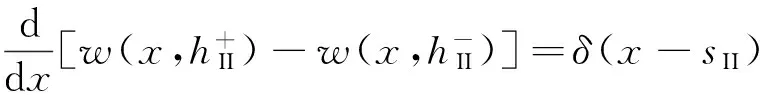
(18)
式中:sI、sII分别为位错点源I和II的横坐标;δ为狄拉克Delta函数。
铁电陶瓷中的位错点源如图2所示,假设铁电陶瓷中仅存在位错点源I,为方便推导,将式(17)等价表示为
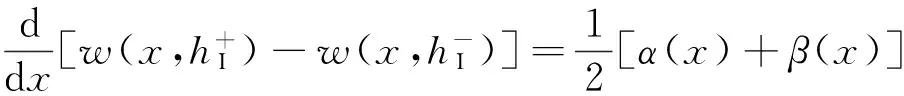
(19)
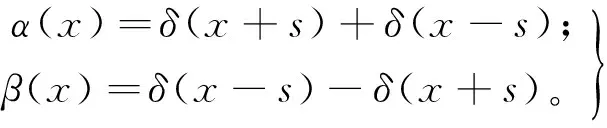
(20)
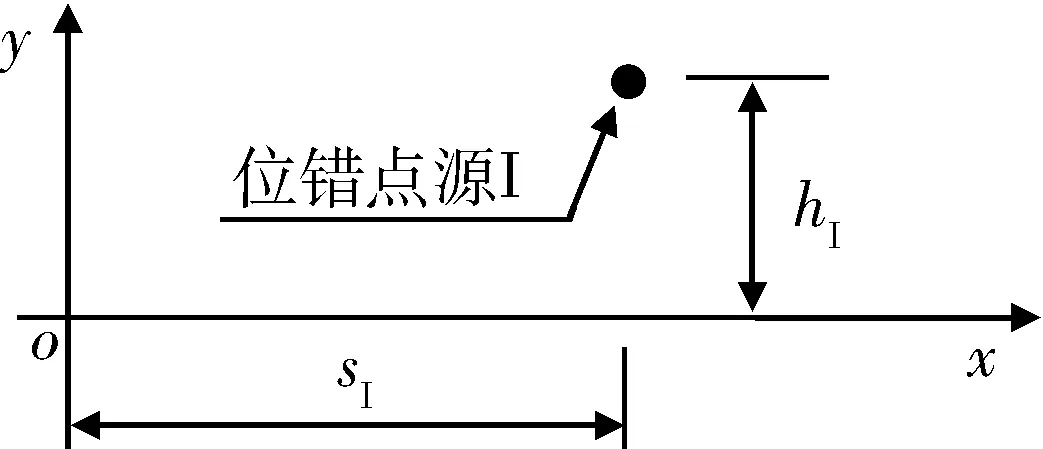
图2 铁电陶瓷中的位错点源
根据狄拉克Delta函数的性质可以推断:α(x)和β(x)分别为偶函数和奇函数。故位错点源I的广义位移场也必然由x的偶函数和奇函数所组成。对式(3)中的控制方程分别进行x的余弦积分变换和正弦积分变换,然后利用式(4)中的边界条件可分别求出位错点源I所产生的广义位移场的对称和反对称部分,进行叠加可得不同区域的广义位移场:
F1e-ξysin(ξx)]dξ;
(21)
(F2e-ξy+V2eξy)sin(ξx)]dξ;
(22)
V3eξysin(ξx)]dξ。
(23)
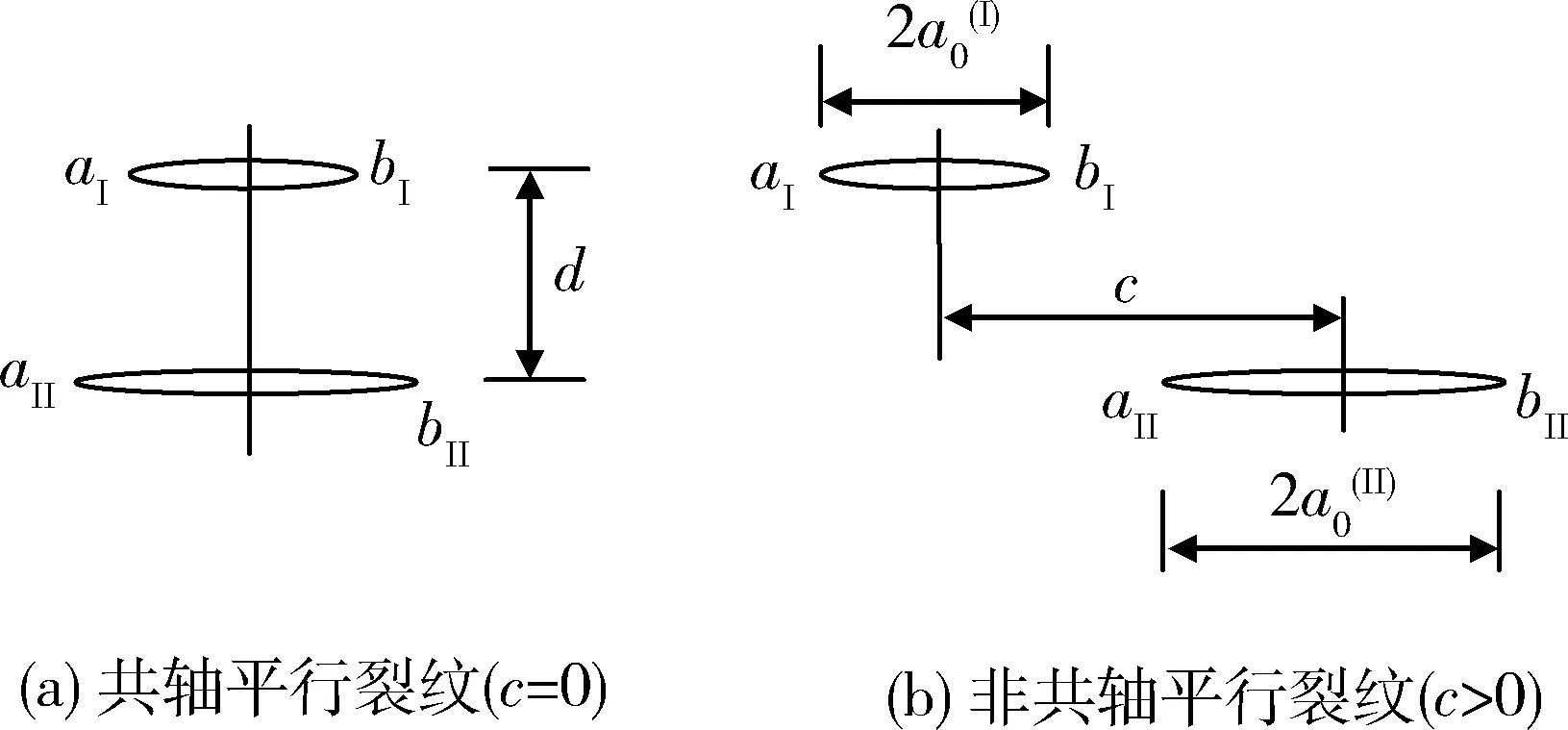
式中:A=(Aw,Aφ)T,C=(Cw,Cφ)T,F=(Fw,Fφ)T,V=(Vw,Vφ)T,均为待定系数向量。下文中,分别用上、下标中的1、2、3标志y≥hI、0 将式(21)-(23)代入式(1)可得位错点源I所产生的广义应力场(略)。将广义应力场和广义位移场代入式(5)-(8)和(19),然后将偶函数和奇函数部分分开,并对所得到的方程相应地进行余弦和正弦变换,可以将它们化为2组代数方程,即附录中j=I时的式(A1)-(A8)和(A9)-(A16)。这2组代数方程具有相同的系数矩阵,记作MI。分别求解2组代数方程可得 (24) 式中:ak1(k=3, 4, 5, 6)为MI的逆矩阵元素。 结合式(24)和广义应力场的表达式推导可以得到位错点源I在y=hI和y=hII所产生的剪切应力的格林函数分别为 (25) QI(ξ)=c44(a31e-ξh2-a41eξh2)+e15(a51e-ξh2-a61eξh2)。 (26) 当ξ→∞时,QI(ξ)的极限值为0。于是,利用积分公式[2] (27) 可将式(25)化为 (28) (29) 对位错点源II进行类似的理论推导,可将式(6)-(8)和(18)化为代数方程组。进一步可得位错点源II在y=hI和y=hII所产生的剪切应力的格林函数分别为 (30) (31) 式中:bk1(k=1, 2)为附录中代数方程组系数矩阵MII的逆矩阵元素。 2.2Cauchy奇异积分方程组 基于Green函数理论,利用式(28)中的格林函数,可以将式(13)所定义的连续分布位错在y=hI和y=hII所产生的剪切应力分别表示为 (32) 同理,采用式(30)中的格林函数,可以将式(14)所定义的连续分布位错在y=hI和y=hII所产生的剪切应力分别表示为 (33) 将式(32)、(33)对应相加,可以得出上述位错在y=hI和y=hII共同产生的剪切应力,代入式(11)、(12),并对结果进行线性变换处理,可得一组具有标准形式的Cauchy奇异积分方程: (34) (35) (36) 根据奇异积分方程理论,式(34)中的位错密度函数的解可表示为[5] (37) 将式(37)代入式(15)、(16)和(34),然后采用配点法,可将其离散为如下代数方程组[5]: (38) 式中:k=1,2,…,nI;t=1,2,…,nII;q=1,2,…,m,其中m为求积节点的个数;λ0=λm=1/2;λ1=λ2=…=λm-1=1; (39) 2.3应力强度因子 反平面裂纹的应力强度因子(SIF)定义为 (40) (41) 2组裂纹左、右尖端处的奇异应力为 (42) (43) 将式(41)、(42)相应地代入式(40)、(41),经进一步推导可得 (44) (45) 在实际工程中,BaTiO3是一种广泛应用的铁电材料,因此假设图1中的铁电陶瓷为该材料。数值计算时,裂纹面等效载荷-τ0=-5 MPa。相关材料参数如下[2]:c44=4.3×1010N/m2;e15=11.6 C/m2;ε11=1.12×10-8C2/(N·m2)。通过计算,探讨平行裂纹之间的相互作用规律。为确保SIF数值计算结果的正确性,需首先明确数值计算的精度。 3.1计算精度 图3 无量纲核函数的收敛行为, 3.2平行裂纹之间的相互作用 图4 2条平行裂纹的间距示意图 假设2组平行裂纹分别只有1条裂纹。按2条裂纹共轴(即它们的中心位于同一条铅垂线上)和不共轴2种情况(见图4),分别通过改变纵、横2个方向的间距c和d来分析裂纹尖端SIF的变化特征,并在此基础上揭示2条平行裂纹之间的相互作用规律。 3.2.1共轴平行裂纹之间的相互作用 图5为2条共轴平行裂纹的SIF随其横向间距d变化的关系曲线。由于此时几何模型在水平方向上关于2条裂纹的中心轴线左右对称,故同一裂纹2个尖端的应力场将始终具有相等的SIF。在图5(a)中,2条共轴平行裂纹等长,故它们的SIF相等。观察图5(a)可以发现:若减小2条裂纹的横向间距d,则它们的SIF将会相应地减小。该现象称为2条平行裂纹之间的“屏蔽效应”,当2条共轴平行裂纹等长时,它们所受的屏蔽作用相同。在图5(b)中,2条共轴平行裂纹不等长,故它们的SIF不相等。观察图5(b)可以发现:较短的裂纹会受到显著的屏蔽作用,而较长的裂纹却基本不受屏蔽。这主要是因为较长的裂纹对较短的裂纹的尖端变形场起到了一定程度的“放松”作用,而反过来后者对前者的尖端变形场却基本没有作用。 图5 2条共轴平行裂纹的SIF随横向间距d变化的关系曲线 3.2.2非共轴平行裂纹之间的相互作用 图6为2条非共轴平行裂纹的SIF随其纵向间距c变化的关系曲线。可见:在SIF变化规律方面,尖端aII和bI相似;尖端aI和bII相似。 1)尖端aII和bI的SIF变化情况。若c从0开始逐渐增大,则尖端aII和bI会逐渐由外侧尖端转变为内侧尖端。在这一变化过程中,其SIF具有3个阶段的典型变化特征:(1)当c从0刚开始变大时,尖端aII和bI逐渐向相邻的裂纹中部移动,它们会因此受到越来越强的屏蔽作用,其SIF会逐渐减小;(2)当SIF的变化超过其局部最小值所对应的c值范围后,若继续增大c值,则2条裂纹相互屏蔽的作用就会逐渐弱化直至最后消失,然而,尖端aII和bI应力场相互干涉的作用却会逐渐增强,其SIF会逐渐增大;(3)当SIF的变化超过其局部最大值所对应的c值范围后,若继续增大c值,则尖端aII和bI应力场相互干涉的作用会逐渐弱化直至最后消失,其SIF会逐渐减小至其稳定值。 图6 2条非共轴平行裂纹的SIF随纵向间距c变化的关系曲线(nI=nII=1,hI=7 mm,hII=5 mm) 2)尖端aI和bII的SIF变化情况。随着c从0开始逐渐增大,尖端aI和bII一直位于外侧,其SIF具有2个阶段的典型变化特征:(1)若c从0开始逐渐增大,则尖端aI和bII所受的屏蔽作用会逐渐弱化,然而,若c值变化超过某个范围,则尖端aI和bII之间就会逐渐出现相互干涉,而且干涉作用会越来越强,其SIF也可能会出现增长;(2)当SIF的变化超过其局部最大值所对应的c值范围后,若继续增大c值,则内侧尖端的相互干涉作用会弱化,而外侧尖端aI和bII所受干涉作用的影响也会弱化,其SIF会逐渐减小,最终达到其稳定值,当达到稳定状态后,同一裂纹左、右尖端的SIF相等。 此外,在2条非共轴平行裂纹不等长的情况下,较短的裂纹往往对纵向间距c的变化表现得更为敏感。 针对铁电陶瓷中的2组平行多裂纹,采用积分变换法、位错模拟法和格林函数法,推导了相应的奇异积分方程组,并利用配点法进行了数值求解。通过对应力强度因子的数值计算结果进行参数分析,揭示并解释了平行裂纹之间相互作用的“屏蔽效应”和“干涉效应”,为工程中铁电陶瓷智能结构的防断裂优化设计提供了理论依据。然而,平行裂纹问题仅是铁电陶瓷开裂方面的一类简化的特殊问题,对实际铁电智能结构而言,不同裂纹之间可能会具有多样化的相对位置关系,相应的断裂力学理论分析过程会变得更加复杂,裂纹之间的相互作用也会呈现出更丰富的特征,相关规律尚有待进一步研究。 附录 (A1) (A2) (A3) (A4) (A5) (A6) (A7) (A8) (A9) (A10) (A11) (A12) (A13) (A14) (A15) (A16) 式中:j=I,II,分别对应位错点源I、II。式(A1)-(A8)组成的方程组与式(A9)-(A16)组成的代数方程组具有相同的系数矩阵,记作Mj(j=I,II),其为8阶方阵,其元素按照上述方程的顺序确定。 [1]ScottJF.ApplicationsofModernFerroelectrics[J].Science, 2007, 315(5814): 954-959. [2]LiYD,FengFX,ZhaoH.MultipleInterfacialCracksinaBi-laye-redMultiferroicCompositeunderMagnetostrictionorElectrostriction[J].EngineeringFractureMechanics, 2012, 90 (1): 65-75. [3]YangJS.AnIntroductiontotheTheoryofPiezoelectricity[M].US:Springer,2005: 31-58. [4]LiYD,LeeKY,FengFX.Magnetostrictive/ElectrostrictiveFractureofthePiezomagneticandPiezoelectricLayersinaMultiferroicComposite:Anti-planeCase[J].InternationalJournalofSolidsandStructures, 2011, 48 (9): 1311-1317. [5]TheocarisPS,IoakimidsNI.NumericalIntegrationMethodsfortheSolutionofSingularIntegralEquations[J].QuarterlyofApp-liedMathematics, 1977, 35 (1): 173-183. (责任编辑: 尚彩娟) Interaction Laws among Parallel Cracks in Ferroelectric Ceramics ZHOU Kai1, LU Shi-yong2, LI Yong-dong1 (1. Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China;2. PLA Military Representative Office in No.618 Factory, Beijing 100072, China) The fracture mechanics theoretical model is established for the problem of parallel cracking in thexoyplane of transversely isotropic BaTiO3ferroelectric ceramics that is polarized along thez-axis. The methods of integral transform, dislocation simulation and Green’s functions are employed to derive the Cauchy-type singular integral equations for the cracks, which are further transformed into algebraic equations by the collocation method. The intensity factors of the crack tip stress field are determined by numerically solving the algebraic equations. Finally, a simple example that only involves two parallel cracks is taken to make parametric studies. The effects of the longitudinal space and transverse space between the two cracks on the stress intensity factors are discussed in detail, and then the shielding and interference phenomena between the two parallel cracks are quantitatively revealed. The obtained results can serve as theoretical references for the anti-fracture optimal design of structures that are made of ferroelectric ceramics. ferroelectric ceramics; parallel cracks; shielding effect; interference effect 1672-1497(2016)04-0098-07 2016-05-15 国家自然科学基金资助项目(11372358) 周凯(1991-),男,硕士研究生。 O346.1 A 10.3969/j.issn.1672-1497.2016.04.020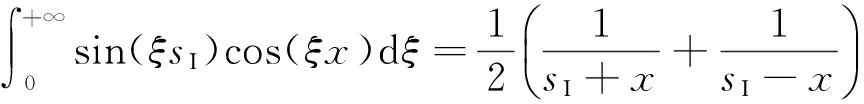
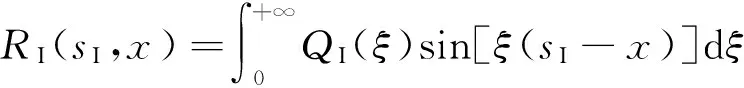
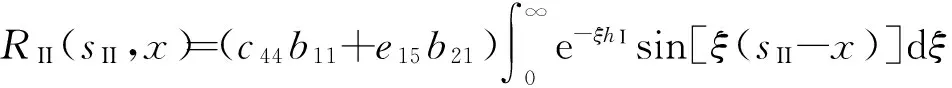
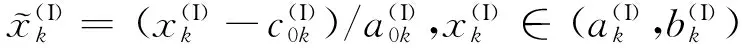
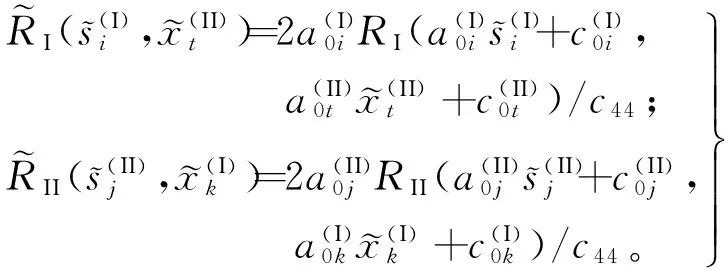
3 数值计算与讨论
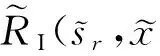
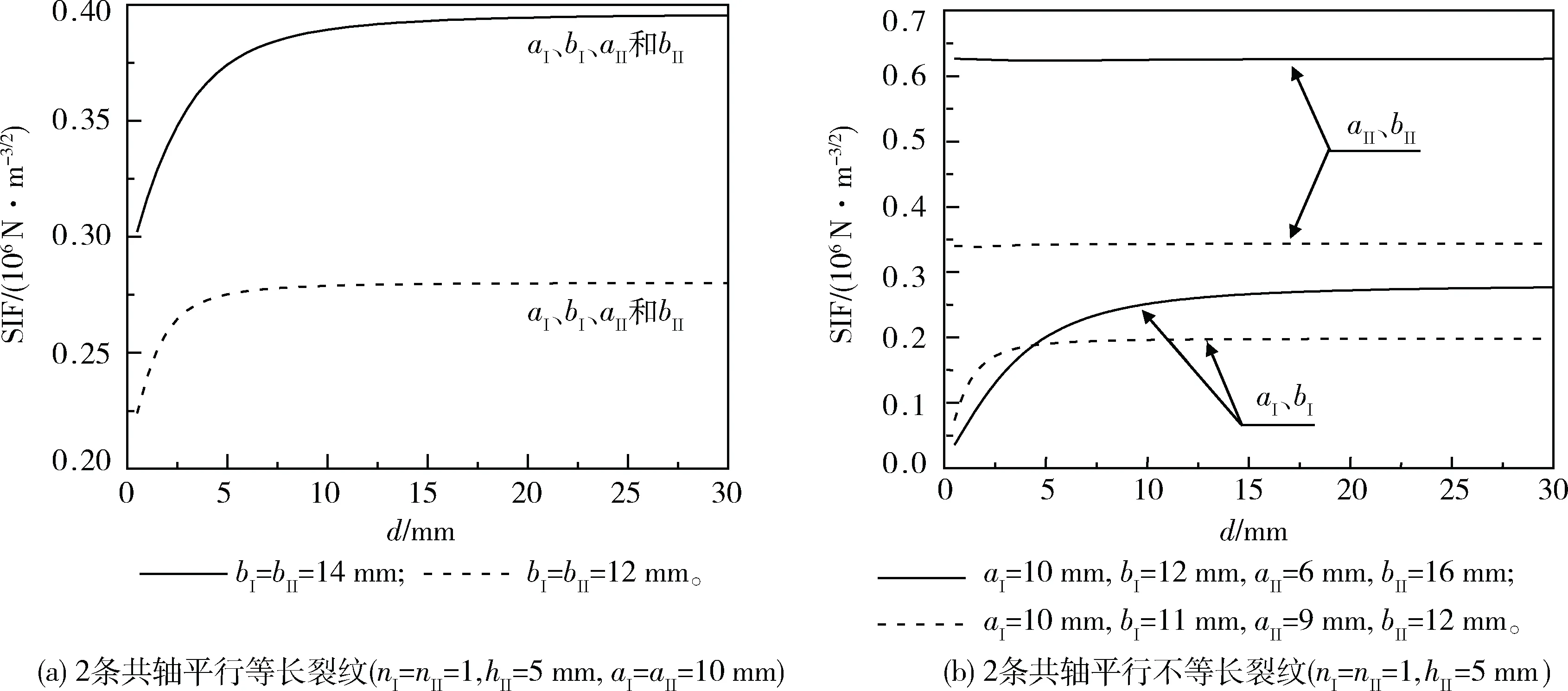
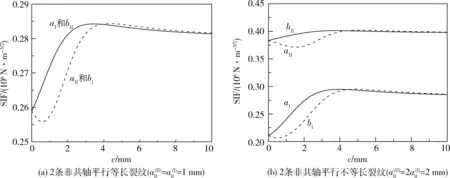
4 结论