大规模MIMO中基于GSSK系统的稀疏检测算法*

陈发堂，丁月友，冯永帅

（重庆邮电大学 重庆市移动通信技术重点实验室，重庆 400065）



大规模MIMO中基于GSSK系统的稀疏检测算法*

陈发堂，丁月友，冯永帅

（重庆邮电大学 重庆市移动通信技术重点实验室，重庆 400065）

广义空移键控（GSSK）的特点是在每一时隙只激活部分发射天线，利用激活天线的索引号来传递信息。基于最大似然（ML）准则的GSSK检测器有最优的检测性能，但计算复杂度太高。为了在性能和复杂度之间取得更好的折中，改进了一种基于压缩感知（CS）的GSSK检测算法。仿真结果表明，该算法的检测性能接近于ML算法，且复杂度约为ML算法的2%。

广义空移键控；最大似然；稀疏性；压缩感知

中文引用格式：陈发堂，丁月友，冯永帅.大规模 MIMO中基于 GSSK系统的稀疏检测算法［J］.电子技术应用，2016，42 （7）：107-110.

英文引用格式：Chen Fatang，Ding Yueyou，Feng Yongshuai.Sparse detection algorithm based on GSSK in large-scale MIMO［J］. Application of Electronic Technique，2016，42（7）：107-110.

0　引言

在大规模MIMO系统中，一个重大的突破是提出了GSM（Generalized Spatial Modulation）和广义空移键控（Generalized Space Shift Keying，GSSK）技术。GSM调制比GSSK调制具有更高的频谱效率，但是GSM有更高的检测复杂度。在发射端，GSSK和GSM只激活小部分的天线，发射端的功耗以及射频链的数量大大减少［1-3］。本文主要研究GSSK的检测算法。

GSSK中的最大似然（Maximum Likelihood，ML）算法需要遍历完所有可能的天线组合，这使得ML的检测计算复杂度相当高，尤其对于大规模天线阵列更为明显。因此，一些次优的检测算法被提了出来，例如压缩感知（Compressive Sensing，CS）算法［4-6］。在文献［4］中，OMP （Orthogonal Matching Pursuit）算法被用于GSSK检测，其仿真结果显示OMP算法相对于许多传统的MIMO检测算法（如MMSE、ZF算法）有更好的性能以及较低的复杂度。但是，随着信噪比的增加，它的BER（Bit Error Rate）出现了地板趋势。在文献［5］中，对H矩阵进行SVD（Singular Value Decomposition）预处理，其GSSK检测性能相应提高，但检测复杂度也相应增加。在文献［6］中，在OMP算法基础上，通过增加迭代次数，使得GSSK的检测性能大大提高，但随着信噪比的增加，BER也逐渐呈现地板趋势。

本文改进了一个基于CS的GSSK检测算法，命名为“ML-OMP-K”。在CS传统的OMP算法里，每次迭代仅仅搜索对应于稀疏集合的一个位置，并且当残余量的范数低于某个阈值或找到的稀疏位置的个数等于实际的稀疏度时，搜索过程停止。但当接收信号遭受到深衰落时，在搜索过程中，有时不能找到正确的稀疏位置。相比OMP算法直接找出AAI（Active Antenna Indices），在改进的ML-OMP-K算法中，先找出一个小的AAI集合，称其为AAI备选集，再利用ML在该备选集中遍历搜索，找出AAI。实际应用中，最终备选集一般较小，在这个集合内进行ML检测所需的复杂度较低，同时可以获得很好的性能。数据结果显示，新算法相比文献［4-6］中的检测算法，有更好的检测性能，且复杂度较低。

1　GSSK系统模型

假设大规模MIMO系统的发送天线数为Nt，接收天线数为Nr，每一时刻激活天线数为nt，则GSSK系统模型如图1所示。

因为GSSK系统是一个大规模MIMO系统，假设信道为平坦瑞利衰落信道，且信道增益在一个符号周期内保持不变，则系统模型表达式如下：

式（1）中，y∈CNr×1，x∈RNt×1，H∈CNr×Nt，n∈CNr×1分别表示 Nr×1的接收信号矢量、Nt×1的发送信号矢量、Nr×Nt的信道矩阵、Nr×1的噪声矢量，nt为激活天线数，即在发射信号矢量x中有nt个位置不为0，对每个接收天线而言，平均信噪比为ρ。信道矩阵H中的每个元素服从均值为0、方差为1的复高斯分布CN（0，1）。在接收端，信道矩阵H被认为是完全可知的。由于信道矩阵服从独立同分布的复高斯分布，因此该矩阵具有良好的RIP （Restricted Isometric Property）特性。

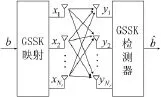
图1　GSSK系统模型

考虑到 GSSK系统中，Nt个发射天线，Nr个接收天线，nt个激活天线。激活天线组合数为可以实现的频谱率为：即有2s个有效的发送符号［4］。然而由于 nt的增加，硬件实现复杂度也相应增加，能量效率相应减少。因此，与文献［4，5］相似，主要考虑 nt＜＜Nt和Nr＜Nt下的GSSK系统。

明显地，ML算法需要遍历完S中所有2s个发送符号集合，其复杂度为因此，在实际系统中，ML算法的复杂度是相当高的。而CS算法利用x的稀疏度特性可以构建出一个可行的检测方案。

2　GSSK检测算法

根据GSSK系统的调制规则，由于x是nt稀疏的，故发送信号矢量x中的大部分位置的元素为0。所以，在接收端的检测可以考虑为是一个稀疏重构问题，即可以

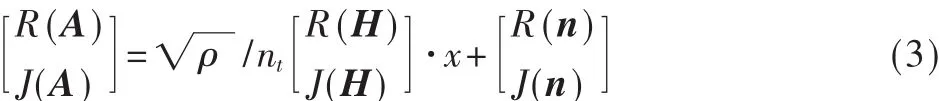
式（3）中R（）和J（）分别表示实部和虚部。进一步将式（3）简写为：

此时y的维度增加了，式（4）中y′∈R2Nr×1，H′∈R2Nr×Nt，x∈RNt×1，n′∈R2Nr×1，则新的观测矩阵 H′的元素服从独立同分布的实高斯分布，显然也具有RIP特性。接下来对H′进行归一化处理：

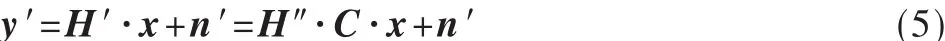
式（5）中的C是一个对角矩阵，对角线上元素Ci，i是矩阵H′的第i-th列的l2范数。那么可得归一化后的等价方程为：

由于H′服从高斯分布，则归一化处理后的新观测矩阵H″显然满足RIP特性。其中，x′=C·x，由于C是对角矩阵，并不影响x的稀疏位置，所以方程仍然是一个压缩感知问题。根据稀疏重构理论，GSSK的检测可以归结为以下l0范数优化问题：利用稀疏重构理论来检测出信号x。

对于稀疏信号，CS算法有很好的信号恢复性能，甚至对于欠定系统也有很好的检测性能。然而，CS算法是基于实数域的，而本系统模型是基于复数域的，因此，在利用稀疏重构之前，需要将式（1）进行变换如下：

在文献［7］中，Tao和Candes已经证明了在RIP特性下，l0范数优化问题可以等价于 l1范数优化问题。

因为l1范数问题可以转换成一个等价的线性规划问题，可以通过MP（Matching Pursuit）类算法有效解决。故已有的OMP算法以及新提出的ML-OMP-K算法均能用于重构原始信号，并且当 GSSK系统满足条件：时，x可以以较高的概率被恢复，其中c为较小的常数［8］。

2.1基于OMP算法的GSSK信号检测

OMP算法是一个贪婪迭代过程［7］。在第 t（1≤t≤nt）次迭代中，将当前残余量rt与观测矩阵 H″作相关运算，OMP会选择出与当前残余量绝对相关值最大的H″的列索引 λt，每次迭代所得的索引作为AAI。然后，每一次迭代都使用最小二乘法来估计t，再用估计值更新残余量。直到迭代结束，得到，再根据恢复出x。OMP算法流程如下所示：

输入：接收信号矢量 y，信道矩阵 H″，信号稀疏度 nt。

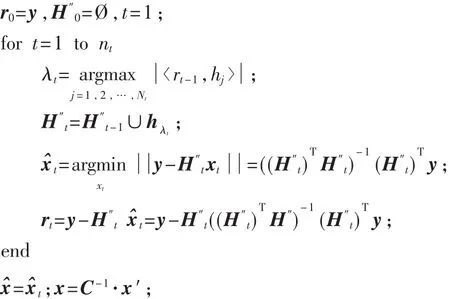
2.2基于ML-OMP-K的GSSK信号检测

明显地，由上述OMP算法可以看出，每次迭代中，OMP仅选取了一个最大的相关值对应的索引号作为AAI，但当接收信号遭受到深衰落时，在搜索过程中有时不能找到正确的稀疏位置。因此，在新的算法中作了相应的改进。

ML-OMP-K算法是在OMP算法基础上进行改进。在第t（1≤t≤nt）次迭代中，将当前残余量 rt与观测矩阵H″的每一列作相关运算，选择出K个最大的与当前残余量绝对相关值所对应的H″的列索引，并存于集合∧t内，此时在∧t内，很大概率地包含了正确稀疏位置。并且记录最大绝对相关值对应的 H″列索引号，记为 λt，用于残差计算。然后每一次迭代都使用最小二乘法估计x，再用估计值来更新残余量。直到迭代结束，可以得到nt个索引集合∧1，∧2，…，∧nt，再从每一个索引集合选取一个元素进行组合，共计 KNt个组合（该值一般很小，因为选取的K和nt都不会太大），存于集合B中，B为第一部分中提到的AAI备选集，将B中所有组合通过ML算法筛选：

输入：接收信号矢量 y，信道矩阵 H″，信号稀疏度 nt。

每次迭代后，取K个最大绝对相关值。

r0=y，H″0=Ø，t=1；

for t=1 to nt计算并找出K个最大绝对相关值，存于集合∧t内。

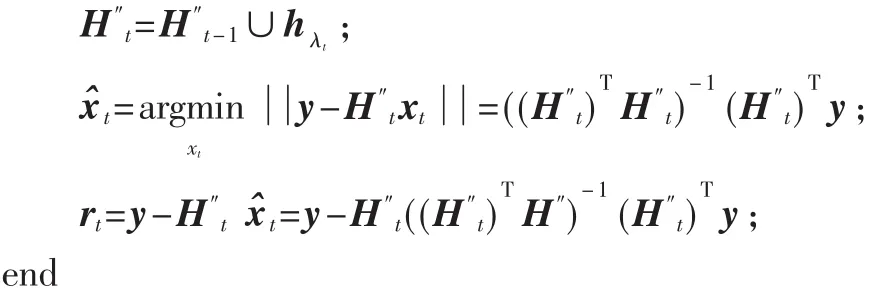
从∧1，∧2，…，∧nt的每一个集合中选取一个元素进行组合，将所有组合存于集合B中。

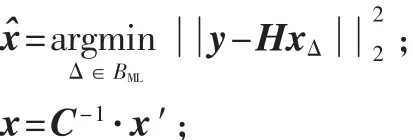
3　性能与复杂度分析

为了验证ML-OMP-K算法的有效性，本节将该算法与ML算法和OMP算法进行性能比较，并分析了算法的复杂度。考虑发射天线数Nt=128、激活天线数nt=2的GSSK系统，系统的频谱效率为s=12 bit/s/Hz。

3.1性能分析

本文给出了在不同接收天线Nr=16、Nr=32下的仿真结果，并将改进的算法与ML算法和OMP算法进行性能对比。

从图2和图3中可以看出，ML-OMP-K的算法性能明显优于OMP算法。图3中显示，在更多接收天线的情况下，ML-OMP-K算法的性能更加接近于ML，同时OMP算法的性能也相应提升。这是因为，对于第二部分描述的GSSK信道模型：

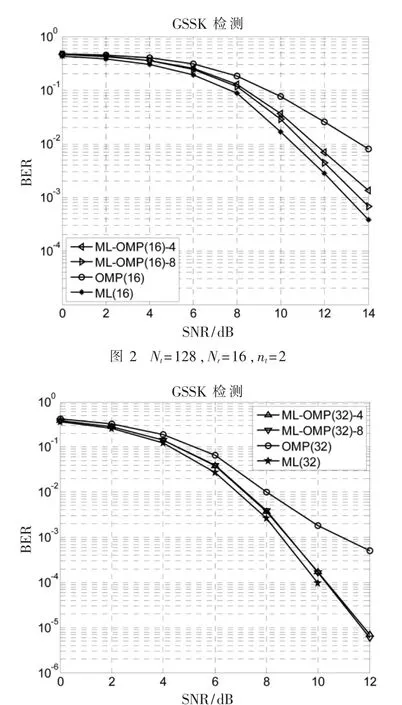
图3　Nt=128，Nr=32，nt=2

明显地，在Nr=16和Nr=32时，当SNR≥10时，OMP算法逐渐呈现出地板趋势。然而，ML-OMP-K算法并没有呈现出地板趋势。相比OMP，当Nr=16，BER=10-2时，ML-OMP-K有至少2 dB的性能优越；当Nr=32，BER= 10-3，BER=10-3.5时，ML-OMP-K分别有大约2 dB和3 dB的性能优越。同时，当K=4与K=8时，ML-OMP-K算法性能相近，且非常接近于ML算法的性能。因此，新的算法对于GSSK信号检测有明显的性能提升。

3.2复杂度分析

用复乘的操作次数来定义复杂度，几种算法的复杂度对比如表1所示。传统的ML检测算法等价于寻找H中对应激活天线nt的列，使下式取最小：

上述过程需要遍历完所有可能的组合，故传统ML检测复杂度约为：o在OMP算法中，首先需要约NrNt次操作来使扩展后的矩阵正交化，然后需要nt次迭代来完成搜索过程，故OMP算法的检测复杂度约为o（ntNtNr）。在ML-OMP-K算法中，与 OMP相关联操作的复杂度约为o（ntNtNr），与 ML相关联操作的复杂度约为o（NrKnt），故 ML-OMP-K算法的检测复杂度约为o（ntNtNr+NrKnt）。因为 nt＜＜Nt，Nr＜Nt，K为一个小的正整数（一般取K=4时，算法就可以达到近似ML的性能），所以ML-OMP-K算法的复杂度也相对较小。

表1　算法复杂度对比

由表 1可得，当 Nt=128，Nr=16，nt=2，K=2（或 K=4）时，以及当 Nt=128，Nr=32，nt=2，K=2（或 K=4）时，MLOMP-K算法的复杂度约为ML算法的2%。

4　总结

本文改进了一种基于压缩感知的GSSK信号检测算法ML-OMP-K。该算法结合了ML算法和OMP算法。首先，在 nt次迭代后，生成一个大小为 Knt的 AAI候选集。再利用ML算法对该候选集遍历搜索，得到对应的AAI。仿真结果显示在K=4时，改进算法的检测性能接近于ML算法，且其复杂度相对于ML算法大大降低。因此，本文改进的算法有较好的实际应用意义，且利于硬件实现。

［1］WANG J，JIA S，SONG J.Generalised spatial modulation system with multiple active transmit antennas and low complexity detection scheme［J］.IEEE Trans.Wireless Commun.，2012，11（4）：1605-1615.

［2］JEGANATHAN J，GHRAYEB A，SZCZECINSKI L.Generalized space shift keying modulation for MIMO channels［C］.In Proc.IEEE PIMRC，2008：1-5.

［3］PEPPAS K，ZAMKOTSIAN M，LAZARAKIS F，et al.Asymptotic error performance analysis of spatial modulation under generalized fading［J］.IEEE Wireless Commun.Lett.，2014，3 （4）：421-424.

［4］YU C M，HSIEH S H，LIANG H W，et al.Compressed sensing detector design for space shift keying in MIMO systems［J］.IEEECommun.Lett.，2012，16（10）：1556-1559.

［5］WU C H，CHUNG W H，LIANG H W.OMP-based detector design for space shift keying in large MIMO systems［C］.In Proc.IEEE GLOBECOM，2014：4072-4076.

［6］SREEJITH K，KALYANI S.Combining ML and compressive sensing：detection schemes for generalized space shift keying［J］. IEEE Commun.Lett.，2016，5（1）：72-75.

［7］CANDES E J，TAO T.Robust uncertainty principles：exact signal reconstruction from highly incomplete frequency information［J］.IEEE Trans.Inf.Theory，2006，52（2）：489-509.

［8］FOUCART S.Hard thresholding pursuit：an algorithm for compressive sensing［J］.SIAM J.Numerical Analysis，2011，49（6）：2543-2563.

Sparse detection algorithm based on GSSK in large-scale MIMO

Chen Fatang，Ding Yueyou，Feng Yongshuai
（Chongqing Key Lab of Mobile Communications，Chongqing University of Posts and Telecommunications，Chongqing 400065，China）

The features of Generalized Space Shift Keying（GSSK）are that only a few antennas are activated at any time slot and antennas indices are exploited to convey information.Though Maximum Likelihood（ML）detector has optimal detection performance，the computational complexity is extremely high.In order to achieve a better tradeoff between the performance and complexity，this paper improves a novel GSSK detection algorithm based on Compressive Sensing（CS）.Simulation results show that the detection performance of the proposed algorithm is similar to ML algorithm and its complexity is about 2%of ML.

GSSK；maximum likelihood；sparsity；CS

TN929.5

A

10.16157/j.issn.0258-7998.2016.07.027

重庆市教委科学技术研究项目（KJ1500428）

2016-01-25）

陈发堂（1965-），男，研究员，硕士生导师，主要研究方向：移动通信和TD-LTE系统开发。

丁月友（1992-），男，硕士研究生，主要研究方向：LTEA系统物理层算法。

冯永帅（1990-），男，硕士研究生，主要研究方向：LTEA系统物理层算法。