连铸中间包内钢液流动特性分析模型的研究进展
2016-09-12郑淑国朱苗勇东北大学冶金学院辽宁沈阳110819
郑淑国,朱苗勇(东北大学冶金学院,辽宁 沈阳110819)
专家论坛
连铸中间包内钢液流动特性分析模型的研究进展
郑淑国,朱苗勇
(东北大学冶金学院,辽宁 沈阳110819)
介绍了中间包内钢液流动特性分析模型的研究进展,针对中间包内钢液的去夹杂流动特性,论述了典型的单、多流中间包去夹杂流动特性分析模型,并通过对比分析找出了较优的单、多流中间包去夹杂流动特性分析模型。对于多流中间包内钢液的流动特性,不仅要考虑非金属夹杂物的去除,还要考虑多流中间包内各流流动特性的一致性,对比分析了典型各流流动特性一致性分析模型的特点并找出了合适的分析模型。所找到的合理的去夹杂及各流流动特性一致性分析模型为中间包内钢液流动特性分析提供了理论依据。
连铸中间包;去夹杂流动特性;各流流动特性一致性;分析模型
连铸中间包是设置在钢包与结晶器之间的冶金反应器,起着减压、稳流、去渣、贮钢、分流等作用。随着对钢质量要求的不断提高,中间包已不仅仅是连铸生产中的一个过渡容器,而是变成具有去除非金属夹杂物、调整钢水合金成分、进行使夹杂物变性和球化的钙处理、均匀钢水成分和温度、调整及控制钢水温度等功能的精炼反应器。在现代连铸的应用和发展过程中,中间包的作用显得越来越重要,其内涵在被不断扩大,从而形成一个独特的领域——中间包冶金[1-2]。
促使非金属夹杂物去除是中间包的重要冶金功能之一,而夹杂物的去除又和其内钢液的流动特性密切相关。若中间包内钢液流动特性良好,则可促使钢液中的非金属夹杂物充分去除;反之,则钢中夹杂物不能充分去除而停留在钢液中,恶化钢水质量。如果中间包内钢液湍流或漩涡严重,则会将中间包保温材料或上部覆盖渣大量卷入钢液,严重污染钢液。对于多流中间包内钢液的流动特性,不仅要考虑非金属夹杂物的去除,还要考虑多流中间包各流流动特性的一致性。原则上,从热量的角度考虑,好的各流流动特性的一致性能保证中间包各流有均匀的钢水洁净度及温度[3],这样才能获得高洁净度的钢水并保证连铸生产的顺行。
为了获得有利于夹杂物去除及各流流动特性一致性好的中间包内钢液流动特性,控流装置如抑湍器、挡墙、挡坝、多孔挡墙、气幕挡墙等被广泛安置到中间包内控流。利用停留时间分布(RTD)曲线来分析中间包内的流动特性已成为研究中间包流场及优化其内控流装置的重要手段[4-12]。显然,能否对中间包内的流动特性做出准确的定量分析,很大程度上取决于所采用的中间包流动特性分析模型是否合适。不合理的分析模型会对中间包流动特性作出误判,进而影响中间包优化控流方案的确定及实际应用效果。本文对连铸中间包内钢液流动特性分析模型的研究进展进行分析,并找出合理的去夹杂及各流流动特性一致性分析模型,为中间包内钢液流动特性分析提供理论依据,并为以后进一步发展完善中间包流动特性评价理论提供参考和借鉴。
1 中间包去夹杂流动特性分析模型
1.1单流中间包去夹杂流动特性分析模型
1.1.1单流中间包组合模型理论
单流中间包最常用的去夹杂流动特性分析模型是组合模型或混合模型。该模型将中间包内流动分为活塞区、混合区及死区[4]。活塞区和混合区的组合称为活跃区,如图1所示[13]。图中,C、θ分别为无因此浓度、无因此时间;V、Vp、Vm分别为中间包的总体积、活塞区体积、混合区体积。活塞区与全混区这两个区的顺序在图1(a)、图1(b)所示两个模型示意图中是相反的。
图2给出了该组合模型的理论RTD曲线[13],图2中,Cmax为无因次峰值最大浓度,θmin为无因次最小停留时间。

图1 活塞区和混合区体积的单流中间包组合模型
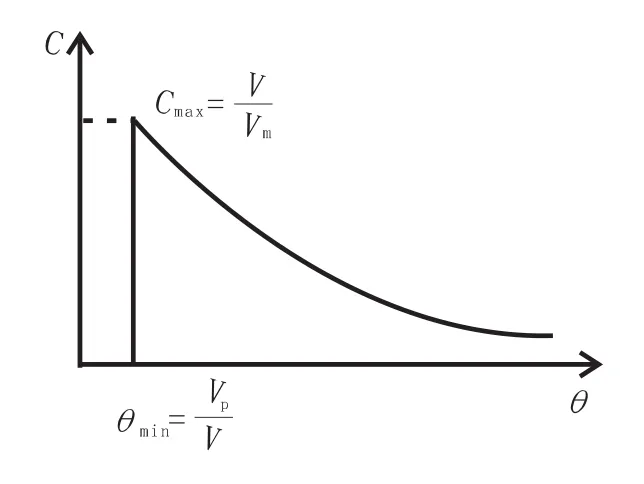
图2 单流中间包组合模型的理论RTD曲线
考虑由活跃区(活塞流和混合流)和死区构成的组合模型。如图3所示[13],体系的总体积分为活跃区体积Va和死区体积Vd。通过体系总体积流量Q也分为通过活跃区的体积流量Qa和通过死区的体积流量Qd。死区有两种类型:一种是完全滞止,甚至来流流体不进入该区域;另一种是该区域内流体运动相当慢,结果一些流体在容器中停留了相当长的时间。通常地,在容器中的停留时间超过两倍理论停留时间的流体被认为是死区体积。

图3 流动组合模型的活跃区和死区
1.1.2典型单流中间包去夹杂流动特性分析模型
1981年,Kemeny等[14]首次提出了一个混合模型来分析单流中间包的去夹杂流动特性,即:


Sahai和Ahuja[4]于1986年指出,上述混合模型存在两大不足,其一是由于中间包内扩散的存在,故θmin≠θpeak;其二是由上述混合模型得到的活塞区、混合区、死区体积分数不能满足式(4)。他们进而提出了修正混合模型。与上述混合模型相比,该修正混合模型死区体积分数的计算公式相同,但活塞区、混合区体积分数的计算公式不同,即:

1996年,Sahai和Emi指出[13],上述混合模型及修正混合模型在求解死区体积分数时均存在较大误差,并提出了修正组合模型,其死区体积分数计算公式为:

在Sahai和Emi提出的修正组合模型中[13],混合区体积分数的计算如式(6)所示,活塞区体积分数计算公式为:


图4 单流中间包典型的RTD曲线
1.1.3典型单流中间包去夹杂流动特性分析模型的对比分析
如上所述,混合模型存在明显缺陷不足,下面重点对目前研究者常采用的修正混合模型及修正组合模型进行对比分析。结合一个具体的单流板坯中间包物理模拟,笔者已对这两个模型的去夹杂流动特性评价进行了对比分析[15]。详细的实验原理及方案见文献15,修正混合模型及修正组合模型对各方案流动特性的分析结果如表1所示,需要说明的是,为便于对比分析,这两个分析模型中,活塞区及混合区体积分数的计算均分别采用公 式(8)和(6)。图5为方案Ⅳ的RTD曲线[15]。
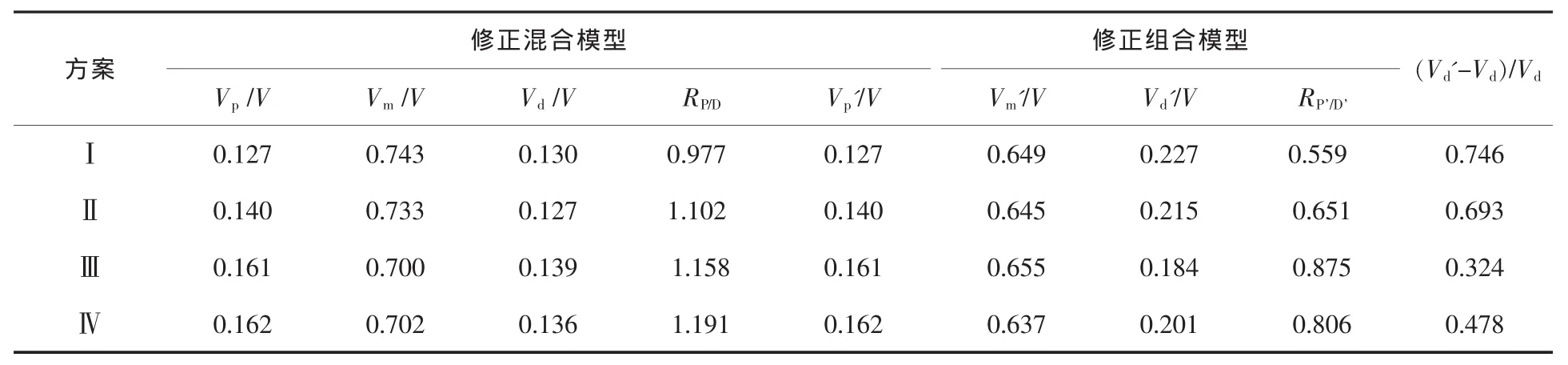
表1 修正混合模型及修正组合模型对各方案流动特性的分析结果

图5 方案Ⅳ的RTD曲线
由图5可以看出,实际测得的无因次RTD曲线上θ从2往后的面积并不为零,而修正混合模型要求该面积为零,故修正混合模型在计算死区体积分数上存在较大误差。由表1可以看出,由修正混合模型得到的死区体积分数的最大误差可达74.6%。利用中间包流动特性优化准则(Vp尽量大、Vd尽量小)对表1综合分析可知,由修正混合模型、修正组合模型得到的最优方案分别为方案Ⅳ和方案Ⅲ,显然这两个模型得到的最优方案不一致。综上,修正混合模型在死区体积分数的计算上存在较大误差,其会对去夹杂流动特性的判断及优化方案的选择造成较大偏差。而修正组合模型能准确的计算死区体积分数,该模型为最优的单流中间包去夹杂流动特性分析模型。
1.2多流中间包去夹杂流动特性分析模型
1.2.1多流中间包组合模型理论
上述Sahai和Emi提出的修正组合模型已被国内外许多研究者采用[9,16-20],但该模型是针对单流中间包去夹杂流动特性进行分析的。目前还没有一个公认的用于多流中间包去夹杂流动特性的分析模型。
多流中间包的组合模型可看作是多个单流中间包组合模型的并联,其活塞区、混合区、死区的体积分别为各个流的活塞区、混合区、死区的体积之和[21-22]。N流中间包的组合模型示意图如图6所示[21-22],图7为其对应的理论 RTD曲线[21-22]。

图6 N流中间包组合模型
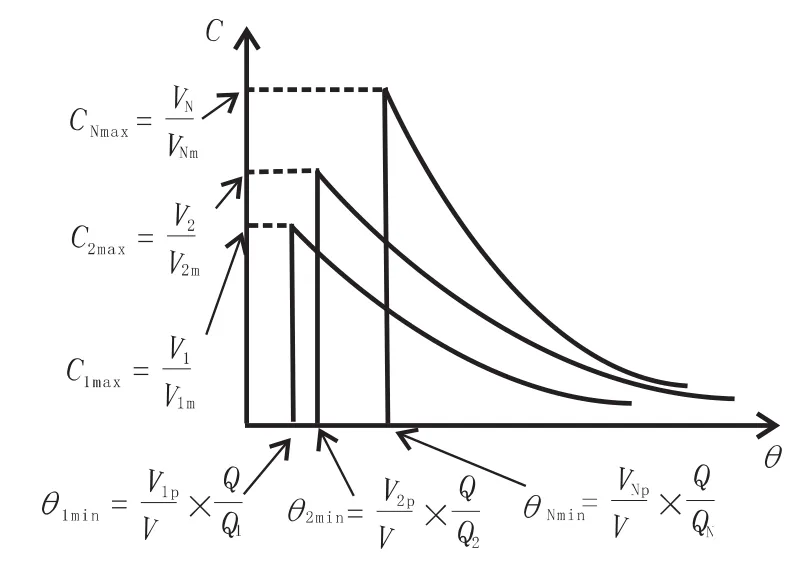
图7 N流中间包组合模型的理论RTD曲线
图6中,Q为该N流中间包的总体积流量,Q1~QN为各流的体积流量。图7中,V,Va,Vp,Vm,Vd分别为中间包的体积、活跃区、活塞区、混合区、死区,V1~VN、V1a~VNa、V1p~VNp、V1m~VNm、V1d~VNd分别为1~N流对应的体积、活跃区、活塞区、混合区、死区体积,θ1min~θNmin为各流的无因次最小停留时间,C1max~CNmax为各流的无因次峰值浓度。
1.2.2典型多流中间包去夹杂流动特性分析模型
目前,典型的多流中间包去夹杂流动特性分析模型主要有五个。
模型Ⅰ[6,23-25]是将多流中间包的每个流都分别应用单流中间包的组合模型,即:


图8 多流中间包典型的RTD曲线示意图
需要说明的是,为了便于模型之间的比较,这里及后边采用的单流中间包组合模型都是Sahai 和Emi提出的修正组合模型[13]。
模型Ⅱ[7,26-28]是在模型Ⅰ的基础上,将各流的相应体积分数分别求平均,即:


模型Ⅲ[3,16,29]是在多流中间包各流RTD曲线的基础上,推导出1条特征RTD曲线,然后对该曲线应用单流中间包的组合模型,即:

式中,E1(t)~EN(t)为各流的停留时间分布密度函数;E(t)为特征停留时间分布密度函数;为特征RTD曲线到点时的实际平均停留时间;为特征RTD曲线活跃区体积流量Q'a与总体积流量Q'之比;θ'min为特征RTD曲线的无因次最小停留时间。
模型Ⅳ[30-34]是在各流RTD曲线基础上求出一个整体平均停留时间,然后再应用单流中间包的混合模型,具体为:

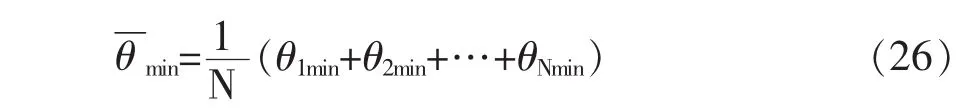
值得注意的是,该模型关于死区体积分数的计算无法应用Sahai和Emi提出的修正组合模型[13]。
模型Ⅴ是笔者在冶金反应器组合模型理论及单流中间包RTD曲线的修正组合模型[13]的基础上,从多流中间包的组合模型理论出发,提出的新的多流中间包去夹杂流动特性分析模型[21-22]。该模型详细的推导过程见文献21和22。该模型为:
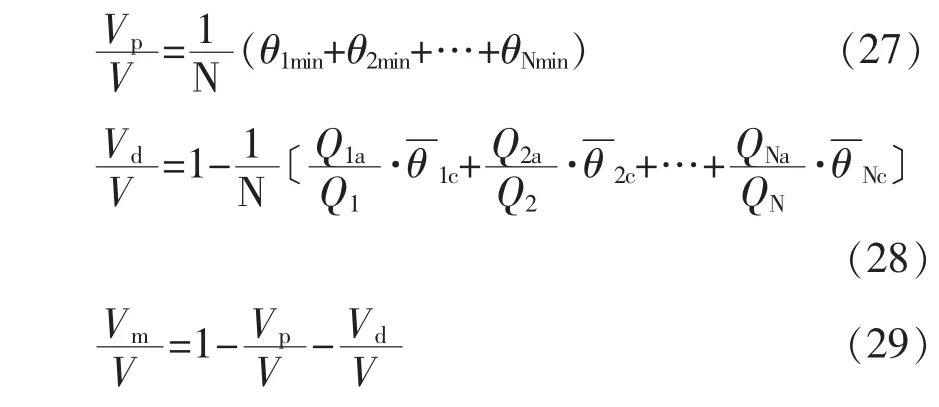
1.2.3典型多流中间包去夹杂流动特性分析模型的对比分析
前两个多流中间包去夹杂流动特性分析模型将单流中间包的修正组合模型直接应用于多流中间包的各流是不正确的。由于用于单流中间包各流区体积分数计算的RTD曲线的一些参数的含义不能直接外扩到多流中间包的RTD曲线,单流中间包组合模型中关于死区、活塞区、混合区的计算方法不能直接应用于多流中间包[16]。由于模型Ⅰ、Ⅱ理论上是错误的,下边重点讨论模型III、IV、V的合理性。
为了比较分析各多流中间包去夹杂流动特性分析模型的合理性,笔者建立了一个六流中间包1:3的物理模型[22]。详细的实验原理及方案见文献22,需要说明的是,此处的方案A对应文献22中的空包,方案B~J对应文献22中的方案I~IX。下面结合该六流圆坯连铸中间包的物理模拟,对上述分析模型III~V进行对比研究,并找出最优的针对多流中间包去夹杂流动特性的分析模型,为多流中间包内的活塞区、混合区、死区体积分数的定量计算提供理论依据。
图9为模型Ⅲ和模型Ⅴ对方案A~J分析得到的活塞区体积分数。由图9可知,模型Ⅲ得到的活塞区体积分数偏小。造成这一结果的原因是由于模型Ⅲ将多条RTD曲线处理成1条曲线,得到的活塞区体积分数只由响应最快的那一流的无因次响应时间决定。具体来说,对于方案B~J,模型Ⅲ得到的活塞区体积分数比模型Ⅴ得到的活塞区体积分数少13.01%~40.36%,该值的大小取决于该方案的最小无因次响应时间与各流无因次响应时间平均值(式(27))的差值。而对于方案A,由于是无控流装置的空包,此值高达97.79%,这是由于无控流装置的中间包内流动极不均匀,各流无因次响应时间相差较大,且最小无因次响应时间明显偏小造成的。可见模型Ⅲ在分析活塞区体积分数时存在一定误差,且有时误差较大。

图9 模型Ⅲ和模型Ⅴ对方案A~J分析得到的活塞区的体积分数
图10为模型Ⅳ和模型Ⅴ对方案A~J分析得到的死区体积分数。由图10可知,模型Ⅳ得到的死区的体积分数偏小。这是由于该模型求死区时无法应用Sahai和Emi提出的修正组合模型[13],具体来说,由于模型Ⅳ是以公式的形式给出一个整体平均停留时间,进而求出死区体积分数,这样就无法求活跃区体积流量与总体积流量的比值(Qa/Q),死区的计算中无法加入Qa/Q(式(23)),如Sahai和Emi所说,这样就会在死区的计算中存在较大误差[13]。模型Ⅳ比模型Ⅴ得到的死区体积分数少了20.91%~26.86%,可见模型Ⅳ在求解死区体积分数时存在较大误差。此外,模型Ⅳ在求活塞区体积分数时,对无因次响应时间简单的取平均值,理论上并没有明确阐述其由来。

图10 模型Ⅳ和模型Ⅴ对方案A~J分析得到的死区体积分数
图11是模型Ⅲ、Ⅳ、Ⅴ对方案A~J分析得到的混合区的体积分数。由图11可知,这三个模型求得的混合区体积分数各不相同。与模型Ⅴ相比,模型Ⅲ和Ⅳ得到的混合区体积分数分别多了0.77%~17.73%和9.86%~11.79%,这主要是由于模型Ⅲ求得的活塞区体积分数及模型Ⅳ求得的死区体积分数均偏小造成的。
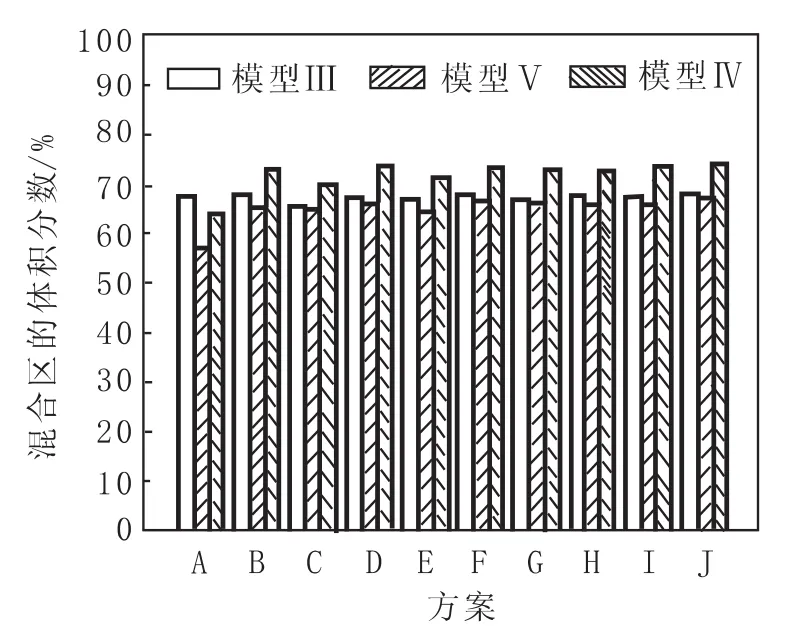
图11 模型Ⅲ、Ⅳ、Ⅴ对方案A~J分析得到的混合区的体积分数
综上可知,模型Ⅲ和模型Ⅳ分别在分析活塞区及死区体积分数上存在较大误差,并造成对混合区体积分数的求解也存在一定误差。因此这两个模型对多流中间包各流区体积分数的求解是不准确的。而模型Ⅴ是基于冶金反应器组合模型理论及单流中间包的修正组合模型[13],从多流中间包的组合模型理论出发,得出的活塞区、死区、混合区计算方法。理论依据充分,且避免了模型Ⅲ、Ⅳ对活塞区、死区求解无法兼顾的局限性,能准确的求解各流区的体积分数,可见模型Ⅴ是分析多流中间包去夹杂流动特性的最优模型,能够为多流中间包内的活塞区、混合区和死区体积分数的准确计算提供理论依据。
需要说明的是,模型Ⅴ与模型Ⅳ计算出的活塞区体积分数结果是相同的,但活塞区体积分数的含义及由来是完全不同的。模型Ⅳ只是简单的对各流无因次时间取平均值,理论上没有具体阐述其由来,且得到的体积分数是平均值。而模型Ⅴ对活塞区体积分数的求解则是在冶金反应器组合模型理论及单流中间包RTD曲线的修正组合模型[13]的基础上推导出来的,得到的是整个中间包的活塞区体积分数,而不是平均值,结果相同只是巧合而已。
2 多流中间包各流流动特性一致性的分析模型
对于多流中间包,为使各流有均匀的钢水洁净度及温度,理想的情况是中间包各流有完全一样的流动特性。但上述情况在实际中间包内腔设计上无法做到。对于一个给定中间包,通过设置合理的控流装置可使各流的流动特性尽可能接近。显然,能否对多流中间包各流流动特性一致性作出准确判定取决于所采用多流中间包各流流动特性一致性分析模型的准确性。
1986年,Knoepke等[35]首次提出一个针对两流中间包的各流流动特性一致性分析模型,该模型利用内、外侧流RTD曲线的峰值最大浓度值的比值来评价各流流动特性一致性,该比值越靠近1,两流的流动特性的一致性越好。Godiwalla等[36-37]指出,上述多流中间包各流流动特性一致性分析模型存在局限性。因峰值浓度值是单个点而易受实验条件影响,故常常会有较大误差;另一方面,该模型不能用于分析超过两流的多流中间包。
Godiwalla等[36-37]提出了一个针对多流中间包的各流流动特性一致性分析模型,即利用最内、最外侧流RTD曲线的面积比(A)来分析各流流动特性一致性,该面积比越接近1,各流流动特性的一致性越好。但该模型也存在不足,因RTD曲线面积是一个总体参数,它不能反映RTD曲线各具体点的特性,一个较好的面积比也无法保证较佳的各流流动特性一致性(见图12)。此外,该模型只对最内侧和最外侧流的RTD曲线面积作比较,因此对超过两流的中间包来说,其它流的流动特性无法得到体现。

图12 一个典型的具有理论上最佳A值(A=1)的RTD曲线示意图
樊俊飞等[26]提出了一个针对多流中间包的各流流动特性一致性分析模型,该模型采用标准差来分析多流中间包各流RTD曲线的最小响应时间、浓度峰值时间和平均停留时间,这些参数的标准差越小,多流中间包各流流动特性的一致性越好。该模型最大的缺点是,分别利用上述三个流动特性特征参数的标准差得到的最优方案往往会不一致[28,38],无法确定最优方案。
笔者提出了一个针对多流中间包的各流流动特性一致性分析模型[22,38]。首先,将各流的无因次RTD曲线在每一个采样时间点下的无因次浓度值(Ci(tj),i=1~N,j=1~Z)求标准差,然后,将整个采样时间范围内的所有标准差取平均值。即:
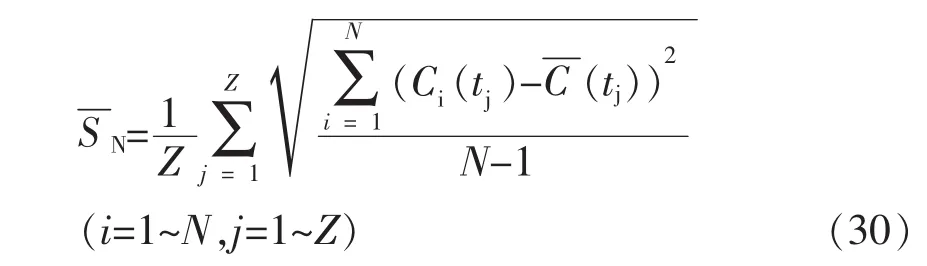
Sengupta等[39]利用笔者提出的各流流动特性一致性分析模型[22,38]作为多流中间包内各流流动特性一致性的定量理论判据,建立物理模型,研究了一个6流中间包内某单流或某双流堵塞对中间包内流动特性一致性的影响。详细的实验原理及方案见文献[39]。表2和3分别为无控流装置及带抑湍器中间包内单流堵塞对各流流动特性一致性的影响,表4则为带抑湍器中间包内双流堵塞对各流流动特性一致性的影响。由表2、3、4可以看出,无控流装置空包内,堵塞3流后各流流动特性一致性比6流全开还要好,而堵塞1流后各流一致性效果较差。中间包内加入抑湍器后,与6流全开相比,除堵塞2流各流流动特性一致性效果变差外,堵塞1流或3流均不会恶化各流一致性效果;而堵塞双流后,除同时堵塞3流和4流会使各流一致性效果变好外,其它两种双流堵塞方式(同时堵塞2流和5流、同时堵塞1流和6流)均会恶化中间包内各流流动特性的一致性。

表2 无控流装置空包内单流堵塞对各流流动特性一致性的影响

表3 带抑湍器中间包内单流堵塞对各流流动特性一致性的影响
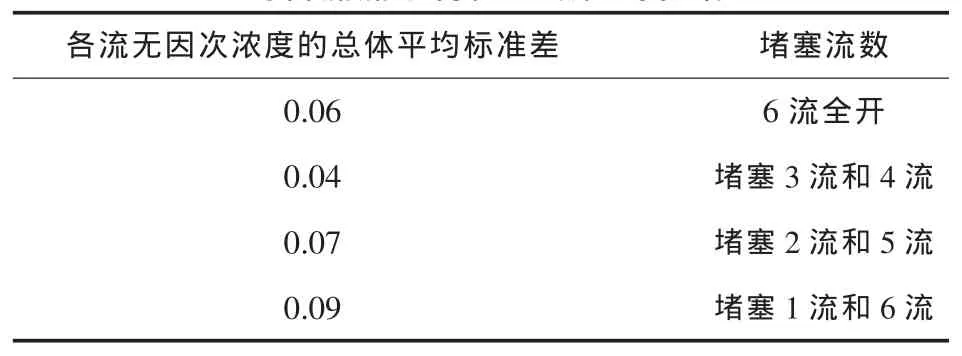
表4 带抑湍器中间包内双流堵塞对各流流动特性一致性的影响
3 结论
连铸中间包已由生产中的一个过渡容器转变成多功能精炼反应器。通过中间包内设置合理的控流装置来获得有利于去夹杂及各流流动特性一致性好的钢液流动,是充分发挥中间包冶金功能的保障。而能否对中间包内的流动特性做出准确的定量分析,很大程度上取决于所采用的中间包流动特性分析模型是否合适。不合理的分析模型会对中间包流动特性作出误判,进而影响中间包优化控流方案的确定及实际应用效果。通过典型单、多流中间包去夹杂流动特性分析模型对比分析找出了较优的去夹杂流动特性分析模型,在对典型多流中间包各流流动特性一致性分析模型对比分析的基础上,找到了合理的各流流动特性一致性分析模型,为中间包内钢液流动特性分析提供理论依据。
[1]K Chattopadhyay,M Isac,R I L Guthrie,et al.Physical and mathematical modelling of steelmaking tundish operations:A review of the last decade(1999-2009)[J].ISIJ int.,2010,50 (3):331-348.
[2]Y Sahai.Tundish technology for casting clean steel:A review [J].Metallurgical and Materials Transactions B,2016,47B(4): 2095-2106.
[3]R D Morales,J de J Barreto,S López-Ramírez,et al.Melt flow control in a multistrand tundish using a turbulence inhibitor [J].Metallurgical and Materials Transactions B,2000,31B(6): 1505-1515.
[4]Y Sahai,R Ahuja.Steel flow and mixing of melt in steelmaking tundishes[J].Ironmaking and Steelmaking,1986,13(5):241-247.
[5]S Singh,S C Koria.Tundish steel melt dynamics with and withoutflowmodifiersthroughphysicalmodeling[J]. Ironmaking and Steelmaking,1996,23(3):255-263.
[6]D Mazumdar,G Yamanoglu,R I L Guthrie.Hydrodynamic performance of steelmaking tundish systems:a comparative study of three different tundish designs[J].Steel Research,1997,68(7):293-300.
[7]郑淑国,朱苗勇,姜桂连,等.四流矩形中间包冲击碗应用水模实验研究[J].钢铁,2004,39(5):23-25.
[8]钟良才,张立,黄耀文,等.湍流控制装置的结构对中间包流体流动特性的影响[J].钢铁研究学报,2002,14(4):6-9.
[9]D F Chen,X Xie,M J Long,et al.Hydraulics and mathematics simulation on the weir and gas curtain in tundish of ultrathick slabcontinuouscasting[J].MetallurgicalandMaterials Transactions B,2014,45B(2):392-398.
[10]G C Wang,M F Yun,C M Zhang,et al.Flow mechanism of molten steel in a single-strand slab caster tundish based on the residence time distribution curve and data[J].ISIJ int.,2015,55(5):984-992.
[11]L C Zhong,L Y Li,B Wang,et al.Fluid flow behaviour in slab continuous casting tundish with different configurations of gas bubbling curtain[J].Ironmaking and Steelmaking,2008,35 (6):436-440.
[12]C Chen,L T I Jonsson,A Tilliander,et al.A mathematical modeling study of tracer mixing in a continuous casting tundish [J].Metallurgical and Materials Transactions B,2015,46B (1):169-190.
[13]Y Sahai,T Emi.Melt flow characterization in continuous casting tundishes[J].ISIJ int.,1996,36(6):667-672.
[14]F Kemeny,D J Harris,A McLean,et al.Fluid flow studies in the tundish of a slab caster[A].Second Process Technology Conference Proceedings[C].Chicago,1981,232-243.
[15]周海斌,郑淑国,朱苗勇,等.宽厚板坯连铸中间罐内钢液流动特性分析[J].材料与冶金学报,2008,7(4):254-257.
[16]D Mazumdar,R I L Guthrie.The physical and mathematical modelling of continuous casting tundish systems[J],ISIJ int.,1999,39(6):524-547.
[17]J Palafox-Ramos,J De J Barreto,S López-Ramírez,et al. Modeling study of the influence of turbulence inhibitors on the molten steel flow,tracer dispersion,and inclusion trajectories in tundishes[J].Ironmaking and Steelmaking,2001,32(4): 615-627.
[18]S López-Ramírez,J De J.Barreto,P Vite-Martínez,et al. Physical and mathematical determination of the influence of inputtemperaturechangesonthemoltensteelflow characteristicsinslabtundishes[J].Metallurgicaland Materials Transactions B,2004,35B(5):957-966.
[19]李丽颖,钟良才,朱英雄,等.板坯连铸中间罐结构优化及应用[J].钢铁,2004,39(增刊):19-20.
[20]R Schwarze,D Haubold,C Kratzsch.Numerical study of effects ofpourboxdesignontundishflowcharacteristics[J]. Ironmaking and Steelmaking,2015,42(2):148-153.
[21]郑淑国,朱苗勇.多流连铸中间包内钢液流动特性的分析模型[J].金属学报,2005,41(10):1073-1076.
[22]S G Zheng,M Y Zhu.Optimisation of baffles in six strand round bloom continuous casting tundish:a physical modelling study [J].Ironmaking and Steelmaking,2006,33(5):398-406.
[23]J Madias,D Martin,M Ferreyra,et al.Design and plant experience using an advanced pouring box to receive and distribute the steel in a six strand tundish[J].ISIJ int.,1999,39(8):787-794.
[24]T Merder,M Warzecha.Optimization of a six-strand continuous castingtundish:Industrialmeasurementsandnumerical investigation of the tundish modifications[J].Metallurgical andMaterialsTransact ionsB,2012,43B(4):856-868.
[25]K Morales-Higa,R I L Guthrie,M Isac,et al.Ladle shroud as a flow control device for tundish operations[J].Metallurgical and Materials Transactions B,2013,44B(1):63-79.
[26]樊俊飞,张清朗,朱苗勇,等.六流T形连铸中间包内控流装置优化的水模研究[J].钢铁,1998,33(5):24-28.
[27]A Kumar,D Mazumdar,S C Koria.Modeling of fluid flow and residence time distribution in a four-strand tundish for enhancing inclusion removal[J].ISIJ int.,2008,48(1):38-47.
[28]F He,L Y Zhang,Q Y Xu.Optimization of flow control devices for a T-type five-strand billet caster tundish:water modeling and numerical simulation[J].China Foundry,2016,13(3): 166-175.
[29]R D Morales,M Díaz-Cruz,J Palfox-Ramos,et al.Modelling steel flow in a three-strand billet tundish using a turbulence inhibitor[J].Steel Research,2001,72(1):11-16.
[30]P K Jha,S K Dash,S Kumar.Fluid flow and mixing in a six strand billet caster tundish:a parametric study[J].ISIJ int.,2001,41(12):1437-1446.
[31]P K Jha,S K Dash.Global optimization of fluid flow and mixing in a six strand billet caster tundish[J],ISIJ int.,2002,42(6):670-672.
[32]P K Jha,S K Dash,S Kumar.Effect of outlet positions,height of advanced pouring box,and shroud immersion depth on mixing in six strand billet caster tundish[J].Ironmaking and Steelmaking,2002,29(1):36-46.
[33]A Tripathi,A S Kumar.Effect of sha pe and flow control devices on the fluid flow characteristics in three different industrial six strand billet caster tundish[J].ISIJ int.,2011,51(10):1647-1656.
[34]S K Mishra,P K Jha,S C Sharma,et al.Effect of blockage of outlet nozzle on fluid flow and heat transfer in continuously cast multistrand billet caster tundish[J].Canadian Metallurgical Quarterly,2012,51(2):170-183.
[35]J Knoepke,J Mastervich.Water modeling inland steel’s No.3 combination caster tundish[A].Warrendale.Steelmaking Conference Proceedings[C]∥Washington:ISS-AIME,1986,777-788.
[36]K M Godiwalla,S K Sinha,C S Sivaramakrishnan.Water model simulation of tundish flow under varying conditions[J].Steel Research,1994,65(7):267-272.
[37]K M Godiwalla,S K Sinha,C S Sivaramakrishnan.Statistical analysis of residence time distribution of fluid elements in continuous casting water model tundish with one side entry[A]. Warrendale.SteelmakingConferenceProceedings[C]∥Chicago:ISS-AIME,1994,703-712.
[38]郑淑国,朱苗勇.多流连铸中间包各流流动特性一致性的判别[J].过程工程学报,2006,6(4):522-526.
[39]A Sengupta,P Mishra,V Singh,et al.Physical modeling investigationofinfluenceofstrandblockageonRTD characteristics in a multistrand tundish[J].Ironmaking and Steelmaking,2013,40(3):159-166.
(编辑许营)
Research Progress of Analysis Model for Flow Characteristics in Continuous Casting Tundish
Zheng Shuguo,Zhu Miaoyong
(School of Metallurgy,Northeastern University,Shenyang 110819,Liaoning,China)
The latest progress of analysis model for flow characteristics in continuous casting tundish is introduced.Typical analysis models to characterize the melt flow for inclusion removal in single-strand and multi-strand tundishes are compared and the optimal analysis models for inclusion removal both in single-strand and multi-strand tundishes are founded.In multi-strand tundishes,besides the inclusion removal,the strand similarity is also need to be taken into account when modifying the melt flow.Therefore,typical analysis models to quantify the similarity among the strands in multi-strand tundishes are analyzed and an optimal analysis model for strand similarity is affirmed.Those optimal analysis models for inclusion removal and strand similarity can provide quantitative theoretical basis for flow characterization in tundishes.
continuous casting tundish;flow characterization for inclusion removal;similarity among the strands;analysis model
TF777
A
1006-4613(2016)04-0001-09
郑淑国,博士,副教授,主要从事洁净钢冶炼理论与工艺研究。E-mail:zhengsg@smm.neu.edu.cn
2016-07-01
