面向光学载荷的臂式指向的加速度反馈补偿

贺 帅HE Shuai（中国科学院长春光学精密机械与物理研究所，长春 130033）

面向光学载荷的臂式指向的加速度反馈补偿

贺 帅
HE Shuai
（中国科学院长春光学精密机械与物理研究所，长春 130033）

光学载荷在轨对目标凝视成像时，需要光轴长时间指向目标。基础振动会对光轴的指向产生影响，从而引起目标成像模糊，为此开展了抑制基础振动影响的加速度反馈补偿研究。以面向光学载荷的3自由度臂式机构为研究对象，首先分析了基础振动对光学载荷指向精度的影响；接着建立了带基础振动的臂式机构的动力学方程，然后根据动力学方程得到了加速度反馈补偿力矩的计算公式；最后采用MATLAB/Simulink与ADAMS联合仿真对加速度反馈补偿方法进行理论验证。仿真验证分两部分进行，分别为不同线振动下的仿真与不同姿态下的仿真。不同线振动扰动与不同姿态下的仿真时，载荷在基础振动与加速度反馈补偿力矩的作用下能保持稳定的指向，验证了加速度反馈补偿方法的正确性。

臂式机构；基础扰动；光学载荷；指向精度；

0　引言

空间技术的发展对空间光学载荷的指向精度、稳定性要求越来越高，特别是在大型巡天望远镜、远距离激光通信等领域。光学载荷的支撑机构［1～4］是保证光学载荷指向精度和稳定性的主要机构。臂式支撑技术是一种新型的光学载荷支撑技术，一般用于大型光学载荷。美国未来将要发展的大型空间望远镜ATLAST［5］、SAFIR［6］望远镜均采用这种技术。然而光学载荷主体的外部扰动会造成光轴与成像目标之间产生相对运动，引起成像质量的下降，这就需要对光学载荷的光轴指向加以控制，保证光轴指向的稳定，实现光学载荷对期望目标的精确指向，为此，本文开展了加速度反馈补偿的研究。

本文以面向光学载荷的3自由度臂式机构为研究对象，将基础振动简化为3个移动关节。首先分析了基础角振动与线振动对光学载荷指向精度的影响；接着采用D-H（Denavit-Hartenberg）建模方法与牛顿-欧拉方程建立了带基础振动的臂式机构的动力学方程，并根据动力学方程得到了加速度反馈补偿力矩的计算公式；最后采用MATLAB/Simulink与ADAMS联合仿真，验证加速度补偿方法的正确性与可行性。仿真模型包括光学载荷在基础线振动下的姿态变化模型和光学载荷在基础线振动与加速度反馈补偿力矩作用下的姿态变化模型。仿真结果表明，在基础线振动与加速度反馈补偿力矩的作用下，光学载荷能保持稳定的指向，验证了加速度补偿方法的正确性。

1　系统介绍

整个系统由光学载荷、驱动轴构成，如图1所示。驱动轴共有三个，呈垂直正交布置。本文采用了简化模型研究三轴控制加速度补偿方法，光学载荷不是主要研究对象，采用模拟负载代替。

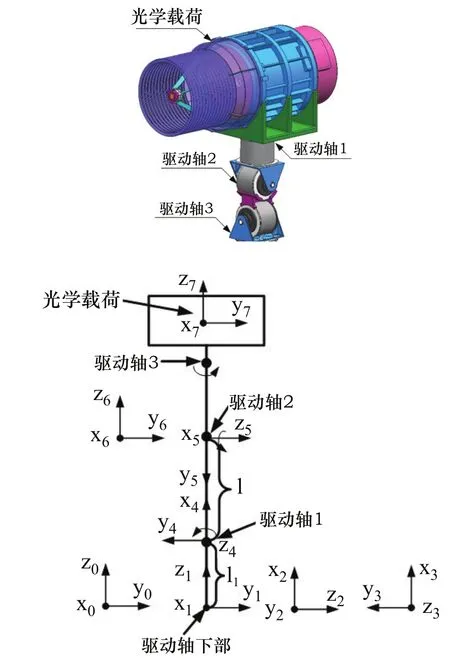
图1　臂式机构的三维模型及连杆坐标系

2　基础振动影响分析

空间光学载荷仅对姿态敏感，这是进行空间光学载荷振动研究的出发点。为简化起见，分析采用如图2所示二维模型，图中a为驱动轴下端线振动加速度，ϕ为角振动加速度。载荷质量为m，电机力矩为M。空间振动分为角振动和线振动，分析针对这两种振动形式开展。

图2　单轴支撑系统示意图

2.1角振动影响

首先分析角振动，由于驱动轴在转动方向仅有电磁力作用，因此驱动轴下端角振动只能通过电磁力传递。驱动轴中的电磁力在系统中采用基于惯性坐标系的闭环控制，其控制信号来源于安装在载荷上的姿态传感器，且控制回路的电流环带宽可达上千赫兹，这些因素能够保证电磁力稳定，受外界干扰影响小。这种情况下，角振动无法通过电磁力传递到光学载荷，其对系统的影响可以忽略。

2.2线振动影响

在偏心的情况下，驱动轴下端线振动也会导致载荷姿态变化，其动力学本质相当于产生了附加惯性力矩，这一点对系统的姿态稳定是非常不利的，需要进行处理。如果能够实时测量振动加速度的大小，进一步计算出附加力矩的值，然后通过驱动轴施加主动补偿力矩，抵消附加力矩的作用，就能够保证姿态不变，这就是本文研究的加速度反馈补偿的基本原理。如图2所示，在线振动a的作用下，若载荷姿态不变，则载荷质心处的加速度也需要为a，此时载荷受到的惯性力为ma，该力相对于驱动轴的惯性力矩为maL。若要载荷姿态不变，驱动轴需要提供的主动补偿力矩为MmaL=-。这就是加速度反馈补偿的控制策略。采用该方法，可以消除基础线振动对姿态的影响，相当于实现了姿态主动振动抑制。

上述分析仅针对单轴情况，若要将其拓展到多轴系统，需要结合正、逆运动学方法建立三轴耦合的系统动力学方程，根据方程设计三轴控制器。

2.3振动影响分析验证

为了验证角振动与线振动对载荷指向精度的影响，本文建立了3种振动下的ADAMS模型，其模型如图2所示。基础与载荷之间用旋转副连接，旋转轴与z轴平行。模型1中基础相对惯性坐标系绕过电机轴线方向转动；模型2中基础相对惯性坐标系沿x轴方向平动；模型3中基础末端相对相对转型坐标系绕y轴转动。仿真模型中杆长0.5m，角加速度φ为t（rad/s2），平动加速度a为0.5t（m/s2）。仿真结果如图3所示。（模型1～3中的振动仅对载荷绕z轴的指向精度有影响，因此仿真结果图中仅提出了X-Y-Z欧拉角的第3姿态角随时间变化的曲线）

图3　振动对载荷指向精度影响

由图3可知，模型1时载荷姿态角保持不变，说明旋转轴段角振动对载荷姿态角没影响；模型2时载荷姿态角发生了变化，说明旋转轴段线振动对载荷姿态角有影响；模型3时载荷姿态角有变化，表明远离旋转轴段的基础角振动（以下简称“偏心角振动”）会对载荷姿态角有影响；模型3时载荷姿态角变化与模型2一样的现象表明偏心角振动对载荷姿态角有影响是因为偏心角振动引起的旋转轴段的线振动影响了载荷的姿态角。

由上面的结果可知，旋转轴段的线振动会影响载荷的姿态角，而其角振动不会，而偏心角振动能等效成旋转轴段的线振动，因此本文后续仅研究了基础线振动对载荷指向精度的影响。

3　动力学建模与加速度反馈补偿

3.1建立连杆坐标系

基础线振动会对望远镜的指向精度有影响，基础线振动有三个自由度，可以简化为3个移动副。因此整个模型可以简化为6自由度串联机器人模型（3个移动副与3个转动副），采用D-H建模方法，各连杆坐标系如表1所示，其中坐标系0～坐标系3的初始原点位置都在分布在驱动轴段，坐标系0为整个模型的惯性参考系，坐标系1～3分别表示3个移动连杆，坐标系4～6分别表示3个转动连杆，其中坐标系5和坐标系6的原点重合。各坐标系z轴方向表示各运动副的运动正方向。

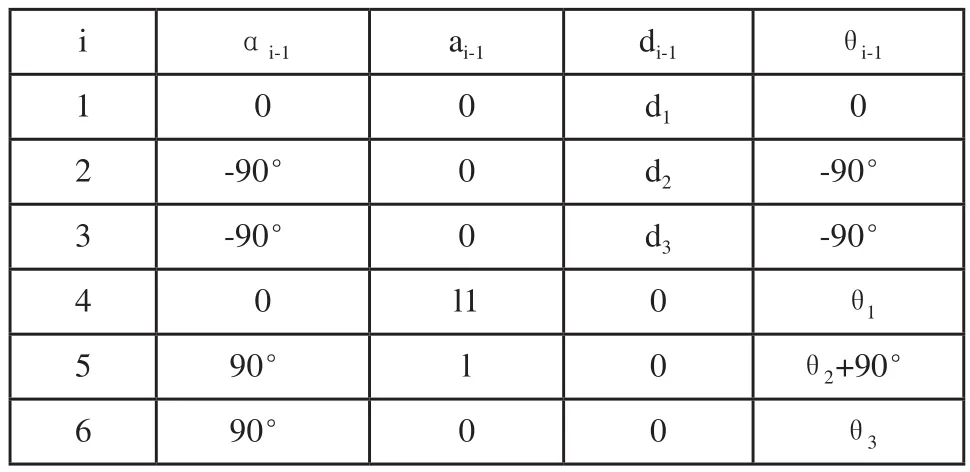
表1　串联机械臂的D-H参数

在D-H参数下连杆坐标系i相对于连杆坐标系i-1的变换矩阵为：

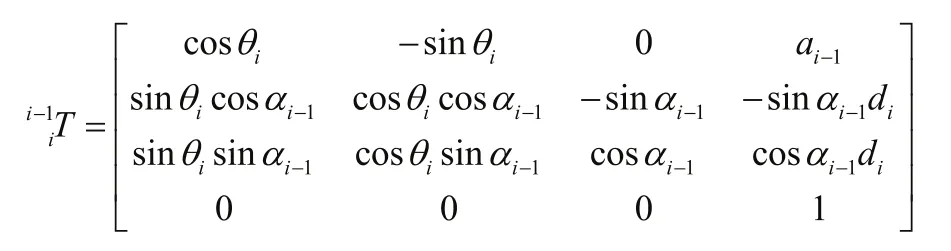
为了计算各连杆受到的合力，需要计算连杆在每个时刻的速度与加速度。速度与加速度的计算可以采用迭代的方法完成，首先计算连杆1的速度与加速度，再计算连杆2的速度与加速度，依此向外计算连杆1～N的连杆的速度与加速度［7］。

1）当连杆i+1关节为转动关节时：

连杆i+1坐标系原点的线加速度在连杆坐标系i+1下的表达式为：

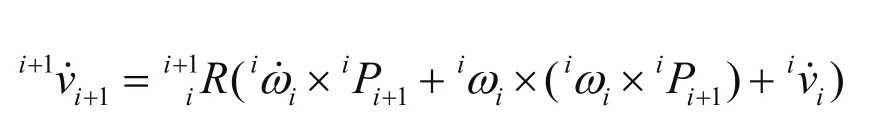
2）当连杆i+1关节为移动关节时：

连杆i+1坐标系原点的线加速度在连杆坐标系i+1下的表达式为：

无论连杆关节是转动关节还是移动关节，连杆i的质心速度在连杆坐标系i下的表达式为：

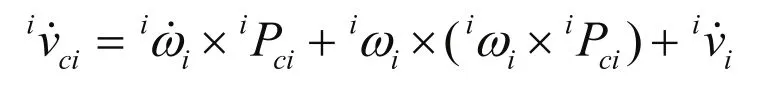
迭代的初始值为：

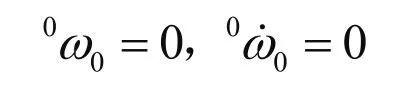
3.3计算各连杆受到的合力与合力矩

利用牛顿欧拉公式可以计算各连杆受到的合力与合力矩：

3.4计算各关节的驱动力

连杆i受力情况如图4所示。图中fi表示连杆i-1作用在连杆i上的力，ni表示连杆i-1作用在连杆i上的力矩。

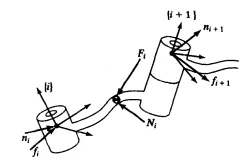
图4　连杆受力分析

将作用在连杆i上的所有力相加得到力平衡方程：

将作用在连杆i上的所有力矩相加得到力矩平衡方程：

重新整理力与力矩平衡方程，形成相邻连杆从高序号到低序号排列的迭代关系：利用公式从末端连杆n向内一直迭代到基座。通过连杆对相邻连杆的作用力在关节坐标系Z向的分量可以得到驱动力（移动关节）或驱动力矩（转动关节）。

为了推导公式需要对一些条件和参数进行约定，主要约定如下：

1）光学载荷的质量为m，驱动轴系的质量与转动惯量远远小于光学载荷的质量与转动惯量，因此忽略驱动轴系的质量与转动惯量；

2）望远镜对称性设计的很好，望远镜转动惯量相对于坐标系6的转动惯量为，望远镜质心相对于坐标系6的位置为<0 0 Pc>；

3）基座线振动扰动加速度分别为Ax、Ay、Az，三轴指向时三个关节转动角度分别为θ1、θ2、θ3。

将上面的参数带入前面的公式并化简得到驱动轴输出力分别为：

3.5加速度反馈补偿力矩

由3.4节中τ4、τ5、τ6公式可以看出，基础线振动影响了驱动轴的输出力矩，将公式中含基础加速度的项提取出来即为为了消除基础线振动对光学载荷指向精度影响，保持光学载荷指向稳定性而施加在驱动轴1～3的补偿力矩：

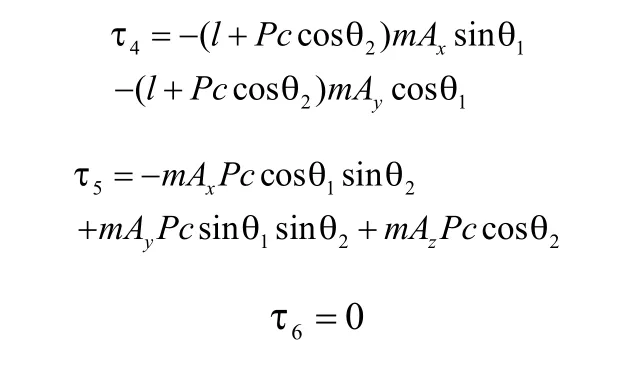
4　仿真验证

本文通过MATLAB/Simulink与ADAMS联合仿真验证加速度补偿公式的正确性与可行性。MATLAB/ Simulink用来计算在基础线振动下3个驱动轴的补偿力矩，ADAMS用来模拟面向光学载荷的臂式机构，并输出光学载荷的姿态角变化。图5为联合仿真流程图。

图5　联合仿真流程图

仿真模型分成2部分：模型1是光学载荷在基础线振动下的姿态变化；模型2是光学载荷在基础线振动与补偿力矩作用下的姿态变化。两种模型下的输出均为望远镜的姿态角。

仿真模型的主要参数如表2所示。

表2　仿真模型主要参数

4.1不同线振动扰动的仿真

首先对不同线振动扰动下的联合仿真来验证反馈补偿力矩公式的正确性。仿真模型的构型对应如图1所示的情况，其驱动轴1～3分别转动0°、0°、0°，扰动1的线振动扰动加速度为：

扰动2的线振动扰动加速度为：

两种振动扰动下载荷第一姿态角（其他姿态角规律一样，因此仅提供了第一姿态角的时变曲线）随时间变化曲线如图6所示。由模型1的曲线可以看出，不同扰动对载荷指向精度影响不同，随着时间的增加，姿态角偏离目标姿态越来越大；由模型2的曲线可以看出，在补偿力矩的作用下载荷指向保持不变，说明了反馈补偿力矩公式的正确性。

图6　不同振动扰动下姿态角时变曲线

4.2不同姿态下的仿真

接着通过对不同姿态角构型下的3轴指向机构的联合仿真来验证反馈补偿力矩公式的正确性。构型2对应如图5所示的情况，其驱动轴1～3分别转动60°、-45° 和30°，对应的光学载荷第一姿态角（载荷坐标系相对于绝对坐标系的Z-Y-X欧拉角）为-0.5236rad。

基础线振动加速度为：

公式中时间单位为s，加速度单位为m/s2。构型2下光学载荷第一姿态角随时间变化曲线如图6所示。由图6与图7中模型1的曲线可知基础线振动会对光学载荷的指向精度有影响；由图6与图7中模型2的曲线可知光学载荷的姿态角保持不变，两种构型下加速度反馈法计算的补偿力矩消除了线振动对光学载荷指向精度的影响，说明了反馈补偿力矩公式的正确性。

图7　构型2下姿态角时变曲线

【】【】

5　结论

本文首先分析了基础角振动与线振动对光学载荷指向精度的影响；接着以面向光学载荷的3自由度臂式机构为研究对象，采用D-H建模方法与牛顿-欧拉方程建立了带基础振动的臂式机构的动力学方程，并根据动力学方程得到了加速度反馈补偿力矩的计算公式；最后采用

MATLAB/Simulink与ADAMS联合仿真，验证加速度补偿方法的正确性。在基础振动与加速度反馈补偿力矩的作用下载荷能保持稳定的指向，验证了加速度反馈补偿方法的正确性。

［1］ 高卫军，孙立，王长杰，等.“资源三号”高分辨率主体测绘卫星三线阵相机设计与验证［J］.航天返回与遥感，2012，33（3）：25-34.

［2］ 王智，李朝辉.月基极紫外相机光机结构设计［J］.光学精密工程，2011，19（10）：2427-2433.

［3］ 姜明，王玉鹏，方伟，等.太阳辐射监测仪跟踪引导系统的设计［J］.电子测量技术，2013，30（9）：84-88.

［4］ 王智，李朝辉.月基极紫外相机光机结构设计［J］.光学精密工程，2011，19（10）： 2427-2433.

［5］ William R O， Lee D F，Lloyd R P. ATLAST-9.2m：a largeaperture deployable space telescope［C］.Space Telescopes and Instrumentation 2010：Optical， Infrared，and Millimeter Wave，Proc. of SPIE，2010，7731：77312M-1-77312M-10.

［6］ Dan Lester，Jason Budinoff，Charles Lillie.Large Infrared Telescopes in the Exploration Era-SAFIR［C］.UV/Optical/IR Space Telescopes： Innovative Technologies and Concepts III，Proc. of SPIE，2007，6687：66870M-1-66870M-10.

［7］ John J.craig，贠超.机器人学导论.3［M］.北京：机械工程出版社.2006：137-139.

The acceleration feedback compensation for the arm type pointing towards the optical load

V447

A

1009-0134（2016）08-0013-05

2016-03-25

贺帅（1989 -），男，吉林长春人，研究实习员，硕士，研究方向为空间遥感器力学分析、机器人运动学与动力学建模。