基于静电法的气力输送局部流动特性R/S分析

王超，张靖宇，张一顺，丁红兵

（天津大学 电气与自动化工程学院，天津，300072）

基于静电法的气力输送局部流动特性R/S分析

王超，张靖宇，张一顺，丁红兵

（天津大学 电气与自动化工程学院，天津，300072）

利用静电电极的局部敏感特性，使用四电极静电传感器对气力输送过程中管道截面局部流动状态进行研究，运用R/S法提取颗粒运动微观特征。研究结果表明：当表观气速上升，静电信号Hurst指数随之下降，颗粒运动复杂度升高，Hurst指数对输送气速变化引起的颗粒运动状态改变具有很好的表征效果。在水平管道截面内，上侧区域静电信号Hurst指数远比左侧、右侧及下侧区域的高，说明上侧区域颗粒运动复杂度较低。当管内流型发生变化时，下侧区域静电信号Hurst指数的相对变化最明显，可以反映颗粒沉积过程。R/S分析法为气力输送流型的研究提供了一种有效的判断方法。

静电传感器；气力输送；流动特性；R/S分析

气力输送在电力、化工和冶金等工业领域应用广泛，理解管道内气固两相流动状态的演化规律，对于节能减排和输送过程的安全稳定具有重要意义。压损是气力输送管内流动状态的重要表征。在固相质量流量一定的条件下，随着输送气速的下降，压损体现为先下降后上升的过程［1］。压损曲线的最低点也是气力输送流型变化的临界点［2］。输送速度高于最小压降速度时，颗粒以悬浮状态存在。输送速度低于最小压降速度，将导致颗粒沉积［3］。但是，由于气固两相流动的复杂性，并且缺乏针对实际管道内部流动状态的测量手段，对于管道内部局部流动特征的演化规律缺少了解。传统的压损分析可以对管内流动状态进行一定程度的表征［4］，但压损只体现气力输送流动的宏观特性，而无法体现管内不同区域的流动状态变化。研究者们使用流场显示技术如LDV和PIV等对气力输送流动特性进行深入分析［5-7］。但LDV和PIV等设备的复杂性、测量范围窄及易受污染等特点决定了其无法针对实际工业管道内部流动状态的变化进行观测［8］。在气力输送的管道中，颗粒之间碰撞，颗粒与管壁之间撞击使颗粒携带电荷，静电传感器利用静电感应原理进行测量，测量信号包含颗粒的运动信息，以此为基础可实现气力输送流动特性的分析［9-11］。本文作者设计了四电极静电传感器，利用4个电极的局部敏感特性，采用R/S分析法研究管内局部静电信号复杂度随气力输送流动状态的演化过程。

1 静电传感器设计与局部敏感特性分析

1.1 四电极静电传感器设计

四电极静电传感器结构示意图如图1所示。静电传感器主要由管道绝缘层、弧形电极组和屏蔽管壁组成。管道绝缘层内径为50 mm。该静电传感器有4个弧形电极，以1～4的数字标记，分别安装于管道截面圆周上侧、右侧、下侧和左侧。电极宽度为 6 mm，弧度为60°。

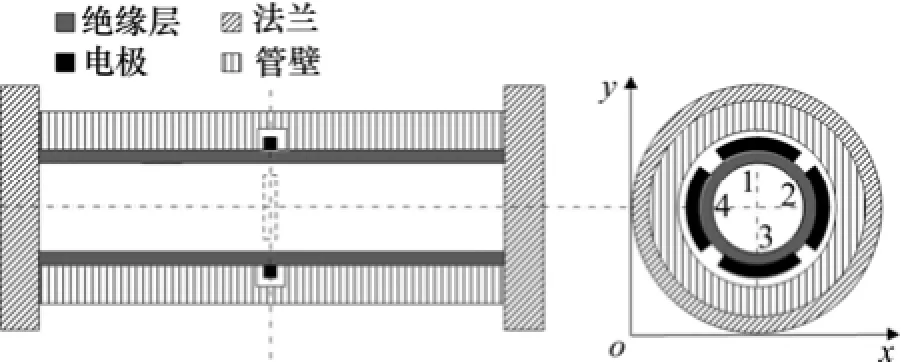
图1 四电极静电传感器结构图Fig.1 Structure of four-electrode electrostatic sensor

1.2 静电场局部敏感特性分析

静电传感器电极的空间敏感度定义为：在敏感空间内，处于某一位置（x， y）的单位电荷，静电感应作用下在电极上产生感应电荷量的绝对值。

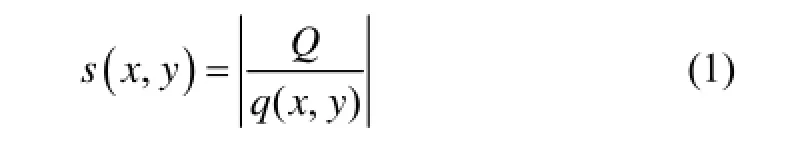
其中：Q为电极上感应电荷量；q（x，y）为点电荷电荷量；s（x，y）为弧形电极在（x，y）位置的空间敏感度。弧形电极2安装于管道右侧，其敏感度分布函数如图2所示。

根据泊松方程，带电颗粒流经静电传感器时，在传感器电极上产生感应电荷是敏感区域内所有带电颗粒共同作用的结果，电极上的感应电荷Q可表示为

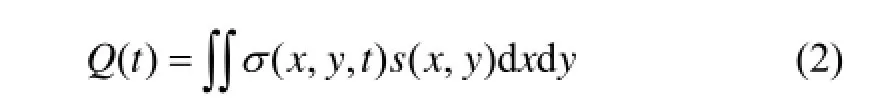
式中：σ（x ，y，t）为t时刻颗粒在传感器内的空间电荷分布函数；s（x，y）为静电电极敏感度分布函数。

弧形静电电极具有局部敏感特性，即靠近电极区域敏感度高，远离电极区域敏感度低，弧形电极静电信号主要表征电极附近区域颗粒的运动信息。四电极静电传感器利用四弧形电极对管内不同区域颗粒运动信息进行分析，得到流动状态变化时管内局部颗粒运动变化规律。

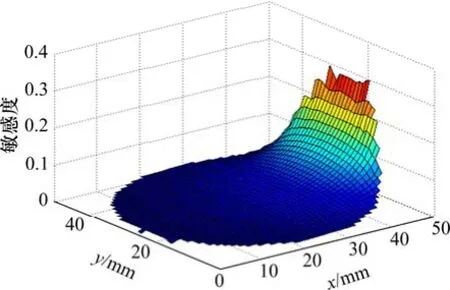
图2 单个弧形电极静电敏感度分布函数Fig.2 Sensitivity distribution function of an arc-shaped electrode

2 局部流动状态的表征参数

R/S分析是处理非线性规律数据的一种方法，起源于分数布朗运动，主要针对随机时间序列的长期相关性和统计自相似性［12］。静电信号间接反映了固相颗粒在输送管道内的流动特性，气固两相流动产生的复杂静电波动信号为类随机信号，所以，静电信号波动程度的大小，反映了静电传感器电极附近敏感区域内的颗粒运动剧烈和复杂程度。

R/S分析的基本思想是：对于给定的时间序列｛xi｝，设置观测次数M，同时将序列分成A个长度为N（2≤N≤M/2）的相邻子区间，AN=M，记第a个子区间为Ia（a=1，2，…，A），Ia中的第k项记作xk,a（k=1，2，…，N）［12］。

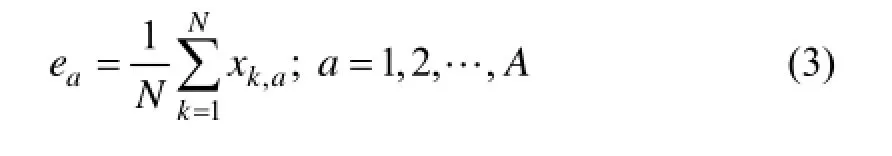
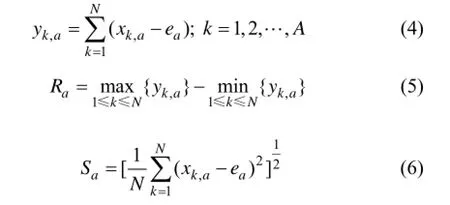
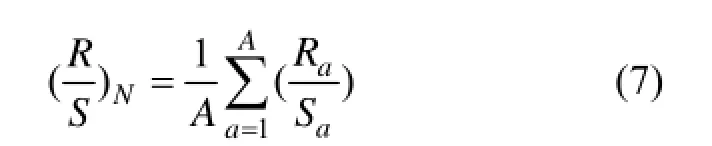
HURST［13］建立等式关系如下式所示，以期比较不同的时间序列。

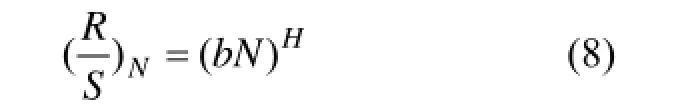
其中：b为常数；H为Hurst指数，且01H≤≤ 。对式（8）两端取对数，可以得到

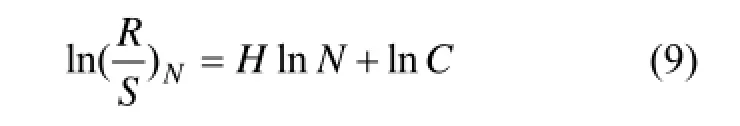
当0＜H＜0.5时，序列具有反持续的特征，即表明时间序列目前的下降（增长）意味后续的增长（下降），或者从另一个角度看，即是时间序列的相关性偏低而且较不规则。H=0.5时，序列是纯随机过程。当 0.5＜H＜1.0时，序列具有正持续的特征，即表明时间序列当前的下降（增长）意味后续的下降（增长）。Hurst指数越接近1.0，静电信号波动规则性越强，说明颗粒微观运动的复杂度越低；Hurst指数越接近0.5，静电信号波动随机性越强，说明颗粒微观运动的复杂度越高。

3 实验装置

气固两相流实验装置为正压气力输送装置，其组成包括空气压缩机、储气罐、干燥系统、气流量计、气路调节阀、输送管道、螺旋给料机、料仓、称量装置和回收罐等，如图3所示。

装置管道口径为 DN50，材质为不锈钢。实验过程中使用的固体颗粒是石英粉，其密度为2.65 g/cm3，粒径范围为96～106 μm。输送气速通过电动阀进行控制，通过气流量计进行测量。颗粒的质量流量通过螺

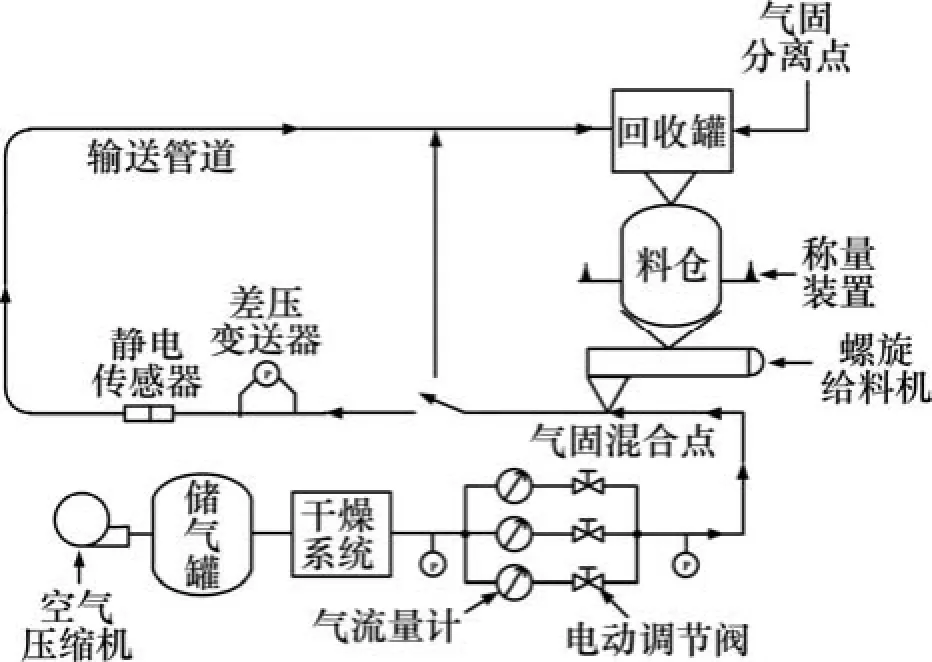
图3 气力输送装置图Fig.3 Schematic diagram of pneumatic conveying test rig

旋给料机进行控制，并且通过装在料斗下面的称重装置进行测量。实验管段前的直管段可以使气力输送流型充分发展，保证实验管段中气力输送流型稳定。四电极静电传感器以及差压变送器安装在水平实验管道上。差压变送器下游取压口与静电传感器中心截面之间距离为0.3 m，可以认为差压变送器测量管段的流型与静电传感器测量管段的流型一致。通过四电极静电传感器对管道内颗粒流动状况进行测量。差压变送器型号为川仪横河EJA120A，量程为0～1 kPa，精度为1%。两取压口安装在长度为1.8 m的水平直管段两端，用来测量水平直管段的压损变化情况。

4 实验数据分析

4.1 直管段压损分析

在实验过程中，保持固相质量流量不变，调节电动阀，逐渐降低管道表观气速，并实时测量实验直管段的压损。直管段压损的实验结果如图4所示。

由图4可见：在纯气情况下，随着表观气速的下降，管道压损基本呈线性下降。当固相质量流量为100 kg/h时，表观气速从约9 m/s继续下降，压损反而增加。这是由于管道内流动状态由管底流向疏密流过渡［14］，同样的情况出现在固相质量流量为120 kg/h时。固相质量流量越大，在同样表观气速条件下，管道压损也越大。当固相质量流量为80 kg/h时，表观气速在8 m/s附近管道压损出现上升点，但是上升点出现后，管道压损没有继续上升，而是很快又下降，与纯气情况下趋于一致。TASHIRO等［15］对此现象进行研究发现：管道固相质量流量过低会导致低气速时压损与纯气时压损趋于一致，在短时间出现疏密流的状态后，管底颗粒很快又被吹起，转化为管底流。

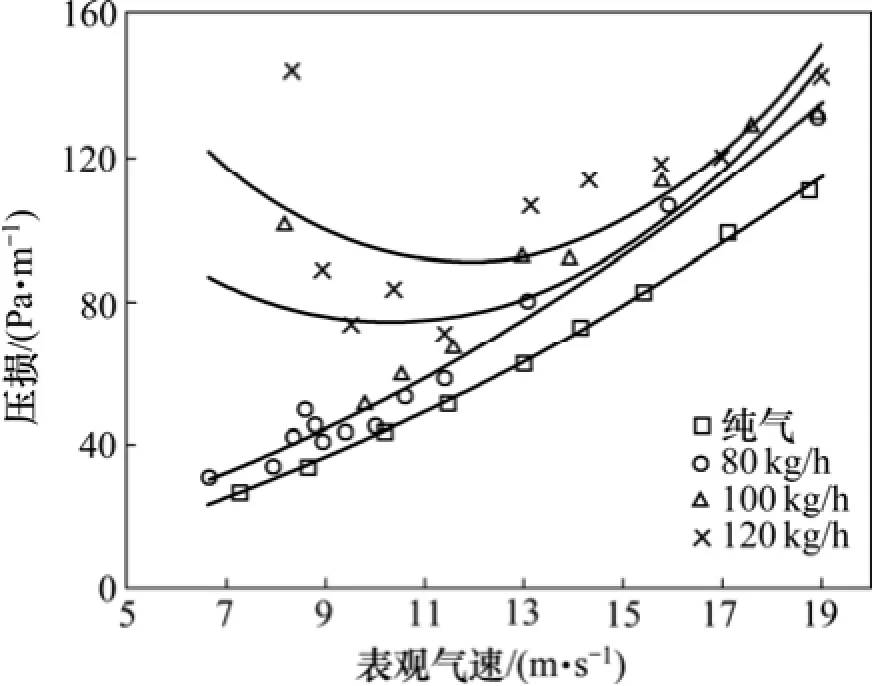
图4 直管段压损随气速及固料流量变化曲线Fig.4 Curve of pressure loss of straight pipe at various gas velocities and solids flow rates

4.2 局部颗粒运动分析

使用R/S分析法对静电信号进行分析，可以得到气力输送流动状态变化时，管内颗粒运动的微观信息。当固定颗粒质量流量为120 kg/h时，改变表观空气速度，使气力输送流型发生变化，对四侧电极静电信号计算Hurst指数，结果见图5。

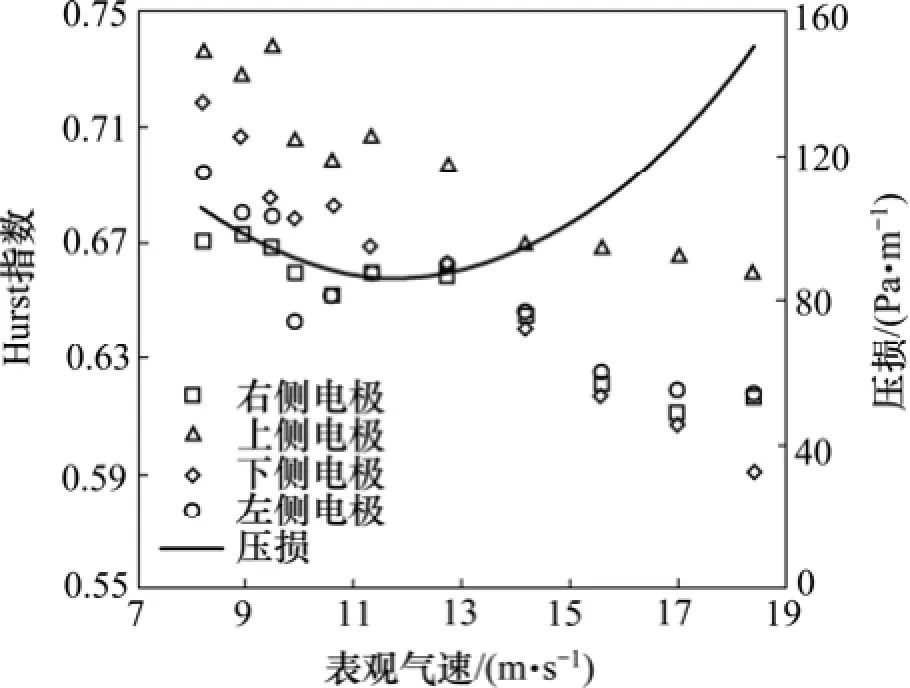
图5 局部静电信号Hurst指数随表观气速变化曲线Fig.5 Curve of Hurst exponent of local electrostatic signal at various gas velocities

静电信号的Hurst指数均大于0.5，说明静电信号的时间序列是具有正的长时间相关效应的有偏随机序列。随着表观气速的升高，管道各个位置的静电信号Hurst指数均表现出线性的下降趋势，颗粒微观运动的复杂度越高，颗粒运动能量越高。在低气速时静电信号Hurst指数较高，说明颗粒的微观运动趋于缓和。

上侧电极静电信号的Hurst指数一直比其他位置电极的高，说明管道上侧颗粒微观运动的复杂度较低。上侧颗粒浓度较其他位置更低，颗粒之间碰撞、颗粒与管道壁的碰撞概率较小。值得一提的是，在表观气速较高时，管道下侧电极附近颗粒的Hurst指数较低，而当表观气速降低到10 m/s以下时，下侧电极的Hurst指数逐渐高于左右两侧。这一现象表明：在10 m/s的表观气速附近管内流动状态发生了剧烈变化，管道底部出现沉积层导致管内下侧颗粒运动逐渐变缓。

通过管道压力降信号对管内流动状态进行分析，可以确定管内固相颗粒大致在表观气速为10 m/s时由原本稳定的管内均匀流向管底流转变，此时管道底部的 Hurst指数开始高于左右两侧，同时管道压力降信号出现不稳定波动。随着表观气速的继续降低，至 8 m/s时，管道底部开始出现明显的沉积层，管内流动状态转变为疏密流，而管道底部的Hurst指数变得更高，同时管道压损开始出现很大幅度的上升，说明管底颗粒的流动逐渐放缓，颗粒的微观运动复杂程度有所下降。

5 结论

1） 随着表观气速的升高，管内各个区域的静电信号 Hurst指数均表现出线性的下降趋势，颗粒微观运动复杂度越高，颗粒运动能量越高。

2） 上侧区域静电信号的Hurst指数一直比其他区域静电信号的高，说明管道上侧固相颗粒微观运动的复杂度较低。

3） 管道底部出现沉积层将导致管内下侧区域颗粒运动逐渐变缓，下侧区域静电信号的Hurst指数由最低变得逐渐高于左右两侧Hurst指数。

4） 通过 R/S法提取四电极静电传感器静电信号的特征，与管道压损进行对比分析，在一定程度上表现出气力输送管内流动状态的变化情况，对于进一步研究气力输送的流型提供了一种有效的判断方法。

［1］ RABINOVICH E， KALMAN H. Boundary saltation and minimum pressure velocities in particle-gas systems［J］. Powder Technology， 2008， 185（1）： 67-79.

［2］ KLINZING G， RIZK F， LEUNG L. Pneumatic conveying of solids： a theoretical and practical approach［M］. Berlin， German：Spring Science & Business Media， 2010： 14-15.

［3］ KALMAN H， RABINOVICH E. Analyzing threshold velocities for fluidization and pneumatic conveying［J］. Chemical Engineering Science， 2008， 63（13）： 3466-3473.

［4］ CONG Xingliang， GUO Xiaolei， LU Haifeng， et al. Flow patterns of pulverized coal pneumatic conveying and time-series analysis of pressure fluctuations［J］. Chemical Engineering Science， 2013， 101： 303-314.

［5］ RINOSHIKA A， YAN F， KIKUCHI M. Experimental study on particle fluctuation velocity of a horizontal pneumatic conveying near the minimum conveying velocity［J］. International Journal of Multiphase Flow， 2012， 40： 126-135.

［6］ JAMA G， KLINZING G， RIZK F. An investigation of the prevailing flow patterns and pressure fluctuation near the pressure minimum and unstable conveying zone of pneumatic transport systems［J］. Powder Technology， 2000， 112（1）： 87-93.

［7］ ZHENG Y， RINOSHIKA A， YAN F. Multi-scale analysis on particle fluctuation velocity near the minimum pressure drop in a horizontal pneumatic conveying［J］. Chemical Engineering Science， 2012， 72： 94-107.

［8］ FOKEER S， KINGMAN S， LOWNDES I， et al. Characterisation of the cross-sectional particle concentration distribution in horizontal dilute flow conveying-a review［J］. Chemical Engineering and Processing， 2004， 43（6）： 677-691.

［9］ XU Chuanlong， LI Jian， GAO Heming， et al. Investigations into sensing characteristics of electrostatic sensor arrays through computational modelling and practical experimentation［J］. Journal of Electrostatics， 2012， 70（1）： 60-71.

［10］ 付飞飞， 许传龙， 王式民. 密相气力输送中气固两相流动特性多源信息分析［J］. 化工学报， 2012， 63（10）： 3070-3079. FU Feifei， XU Chuanlong， WANG Shiming. Multi-sensors integration for flow characterization of dense phase pneumatic conveying of coal powder［J］. CIESC Journal， 2012， 63（10）：3070-3079.

［11］ 付飞飞， 许传龙， 王式民， 等. 基于阵列式静电传感器的密相气力输送煤粉颗粒运动特性分析［J］. 东南大学学报（自然科学版）， 2013， 43（3）： 536-541. FU Feifei， XU Chuanlong， WANG Shiming， et al. Flow characteristics of dense-phase pneumatically conveyed coal powders by electrostatic sensor arrays［J］. Journal of Southeast University （Natural Science Edition）， 2013， 43（3）： 536-541.

［12］ 徐绪松， 马莉莉， 陈彦斌. R/S分析的理论基础： 分数布朗运动［J］. 武汉大学学报（理学版）， 2004， 50（5）： 547-550. XU Xusong， MA Lili， CHEN Yanbin. The basic theory of R/S analysis： fractional Brown motion［J］. Journal of Wuhan University （Natural Science Edition）， 2004， 50 （5）： 547-550.

［13］ HURST H E. Long-term storage capacity of reservoirs［J］. Transactions of the American Society of Civil Engineer， 1951，116： 770-808.

［14］ GOMES L， MESQUITA A. On the prediction of pickup and saltation velocities in pneumatic conveying［J］. Brazilian Journal of Chemical Engineering， 2014， 31（1）： 35-46.

［15］ TASHIRO H， PENG X， TOMITA Y. Numerical prediction of saltation velocity for gas-solid two-phase flow in a horizontal pipe［J］. Powder Technology， 1997， 91（2）： 141-146.

（编辑 杨幼平）

R/S analysis for local flow characteristics of pneumatically conveyed particles using electrostatic method

WANG Chao， ZHANG Jingyu， ZHANG Yishun， DING Hongbing

（School of Electrical Engineering and Automation， Tianjin University， Tianjin 300072， China）

A four-electrode electrostatic sensor with local electrostatic sensibility was used for studying local flow characteristics in the pneumatic conveying process. Moreover R/S method was adopted to characterize the complexity of particle motion. The results show that the Hurst exponent of electrostatic signal has a decreasing trend with the increase of surficial gas velocity， which indicates that the complexity of particle motion increases. Thus the Hurst exponent can represent the particle motion state when the conveying velocity changes. In the horizontal pipe， the Hurst exponent of the electrostatic signal in the top of the pipe is higher than those in other regions. It is demonstrated that the particle motion in the top of the pipe is with low complexity. When the flow pattern changes， the Hurst exponent of the electrostatic signal in the bottom of the pipe changes clearly， which shows the particle deposition. The R/S method is an effective judgment for flow pattern of pneumatic conveying.

electrostatic sensor； pneumatic conveying； flow characteristics； R/S analysis

TB971

A

1672-7207（2016）05-1794-05

10.11817/j.issn.1672-7207.2016.05.045

2015-05-13；

2015-07-05

国家自然科学基金资助项目（61072101） （Project（61072101） supported by the National Natural Science Foundation of China）

王超，博士，教授，从事气固多相流测量研究；E-mail： wangchao@tju.edu.cn