基于二分法的凸多边形内外点判别算法
2016-09-09于凯俞孟蕻
于凯,俞孟蕻
(江苏科技大学 计算机科学与工程学院,江苏 镇江 212003)
基于二分法的凸多边形内外点判别算法
于凯,俞孟蕻
(江苏科技大学 计算机科学与工程学院,江苏 镇江 212003)
多边形内外点判定算法是图形学的基础型算法,目的是判定待测点是否在指定的多边形之内。由于传统的射线法与角度和法效率偏低,平均时间复杂度为O(n),当多边形边数或者待测点个数较多时,算法耗时较高。因此本文分析了传统的射线法与角度和法的缺点;提出了基于二分法的凸多边形内外点判别算法;最后进行实验仿真,证明该算法的平均时间复杂度为O(n/2)。该算法通过递归的分割凸多边形,判断待测点与分割线的相对位置,最终转化为三角形内外点的判别,具有快速、稳定、准确的优势。
凸多边形;二分法;包含测试;递归分割
多边形内外点判别算法也叫做点的包含测试(point-inpolygon test),目的是测试一个点是否在多边形内[1]。该算法在计算机图形学、模式识别、地理信息系统等众多领域中有着广泛的应用。例如,当工业上需要判断矿井是否在指定的区域内,或者游戏中需要判断点击的位置是否在指定的区域内。解决此类问题首先通过仿真,将指定区域建模成多边形,而矿井或者点击的位置就是待测点,通过多边形内外点判别算法判定此待测点是否在该多边形内,从而确定矿井或者点击位置是否在指定区域内。算法的平均时间复杂度也就是判定待测点是否在多边形内的平均耗时,耗时减少,会使得游戏的体验更好,工业上工程的进度更快。因此怎样节省算法的耗时时本文研究的主要问题。边形交点的个数来判断被测点是否在多边形内,若交点个数为偶数,则待测点不在多边形之内,若交点个数为奇数,则待测点在多边形内部。角度和法,通过计算被测点与个顶点连线所形成的角度之和来判断被测点是否在多边形内,若夹角之和为360度,则待测点位于多边形内部,否则待测点不在多边形内部[6]。此类方法虽然易于实现,但是有如下缺点:对于每一个待测点,均需要进行n次判定(n为多边形边数)才能确定待测点的位置,即最优、最差、平均时间复杂度均为O(n);只能判断待测点是否在多边形内,而不能确定待测点的区域。
第二类算法是需要预处理的算法,如网格分割法、分层法等,文献[2-9]采用了预处理的方法。网格分割法首先建立均匀网格,并从左至右依次计算每个网格单元中心点的位置属性,确定待测点所在的网格,再根据点与网格中心点的关系判断待测点的位置[3]。分层法是将多边形的边分层管理,通过判断待测点与每一层的边的关系来确定待测点的位置[5]。此类算法不仅可以判断待测点是否在多边形内,还可以确定待测点的大致区域,此类算法缺点如下:预处理往往比较耗时,不同的预处理结果可能导致算法性能的大幅度波动。例如网格法中,网格的大小对于算法性能的影响很明显,网格过大或者过小均会降低算法的效率;需要额外的存储空间存储预处理结果,在降低算法时间复杂度的同时却增加了算法的空间复杂度。根据是否需要对多边形进行预处理可以将多边形内外点判别算法分为两类,一类是不需要进行预处理的算法,如射线法、角度和法,文献[10]中对射线法进行了改进,算法平均时间复杂度为O(n)。
1 基本约定与算法思想
1.1算法原理与依据
本算法核心思想包括三部分,使用顶点向量组织管理多边形的顶点、使用二分法递归的分割多边形、判断分割线与待测点的相对位置。
由于任意多边形均可以看成是一组点集按照顺时针或者逆时的顺序连线,所形成的封闭图形,因此本算法使用向量的管理多边形的顶点集合,在本算法中称之为顶点向量。每一个多边形均对应唯一一个顶点向量,每一个顶点向量也可以确定一个唯一的多边形[11]。根据当前多边形的顶点总数,使用二分法分割多边形,实际上就是将当前的顶点向量分割成两个新的顶点向量,因此对应两个新的多边形。通过判断待测点与分割线的相对位置,在两个新的顶点向量中选择一个,再次进行分割与判断,如此递归循环,直到当前顶点向量中只有3个顶点为止,此时采用射线法可以轻松的判断出待测点是否在多边形内,同时可以使用这3个顶点确定待测点所在的三角形区域。
1.2顶点向量
顶点向量是一个保存了当前多边形顶点信息的向量。
为了方便管理多边形的顶点,在构造多边形时,将顶点进行有序管理。首先选择所有顶点中横坐标最小的顶点(如果有多个,则选择其中一个),将其作为顶点向量中的第一个顶点,编号为0。然后按照逆时针的顺序将其余各个顶点依次加入顶点向量[12],编号依次加1。顶点向量中的每个节点不仅保存了顶点的横纵坐标,还记录了顶点的编号。当多边形进行变化时,顶点向量也随之更新。
1.3凸多边形的分割
定义1凸多边形是指没有任何一个内角是优角 (大于180度小于360度)的多边形。
定理1连接凸多边形任意两顶点,一定将此凸多边形分割为两个凸多边形。
证明:因为凸多边形的任意两个顶点的连线均在多边形内部,所以,连接任意两个顶点后,会将原有的内角分为两个新的内角。又因为凸多边形的内角全部为非优角,因此产生的新角也一定为非优角,所以分割后的两个多边形仍为凸多边形。
定义2分割线是由左右端点组成的一条线段,其左侧端点固定,为凸多边形顶点向量中的第一个顶点,即横坐标最小的顶点。右侧端点根据当前凸多边形的顶点总数求出。分割线方向朝向x轴正方向,将凸多边形分割为两个凸多边形。
1)求取分割线
给定一个的凸多边形M=V0V1…Vn-1,求取分割线的方法如下:
Step1.在当前凸多边形对应的顶点向量中,选取编号为0的顶点,作为分割线的左端点,记为P0;
Step2.计算当前凸多边形定点个数,记为N。设分割线右侧端点为当前凸多边形顶点向量中的第i个顶点。则i=[N/2]向下取整,记为P1;
Step3.连接P0,P1即为分割线,求得分割线的方程f(x,y)=0。2)待测点与分割线的位置关系
由于分割线的方向固定,都是朝向x轴正方向。因此,将待测点带入分割线方程,若f(x,y)>0,则待测点在分割线上方;若f(x,y)<0,则待测点在分割线下方;若f(x,y)=0,则在分割线所在直线上。
1.4递归分割
递归分割时,分割线左侧端点不动,根据点与分割线的位置关系,将分割后的凸多边形再次进行分割[13]。一个凸多边形经过分割后最终会形成若干个三角形。最终将点与凸多边形的关系转化为点与三角形的关系。
1.5待测点的区域判断
每次分割会造成顶点向量的改变,但是并不改变顶点的相对顺序。当递归分割完成时,顶点向量中只有3个顶点,第一个顶点是分割线的左端点,因此可以使用第二个顶点的编号作为三角形区域的编号。凸多边形的区域划分如图1所示,待测点分布区域的仿真结果如图2所示。

图1 凸多边形的区域划分

图2 待测点的分布区域
从图2中可以看出,待测点被分成了3个区域,分别用三角形、圆圈和方框表示。
2 算法描述
算法主要步骤如下:
1)选择横坐标最大、横坐标最小、纵坐标最大、纵坐标最小的4个顶点(若有多个,选择一个),制作一个矩形包围框。若待测点的横坐标、纵坐标其中一个或者两个均不在此包围框范围内,则判断待测点不在凸多边形之内,算法结束。否则执行2)。
2)计算当前凸多边形的顶点个数N,若N=3,则直接使用射线法进行三角形内外点的判定,否则执行3)。
3)按照1.4节求分割线的方法求出分割线,分割凸多边形为两个凸多边形。判断待测点与分割线的位置关系,即将待测点带入直线方程计算结果记为R。如果R=0且待测点的横坐标在分割线左右端点的横坐标区间内,则待测点在分割线上,也在凸多边形之内,算法结束。否则执行4)。
4)若R>0,则待测点在分割线的上方,删除当前顶点向量中在分割线下方的顶点(不包括分割线的两端点),形成新的凸多边形与新的向量;若R<0,则待测点在分割线的下方,删除当前顶点向量中在分割线上方的顶点(不包括分割线的两端点),形成新的凸多边形与新的向量,执行2)。
3 计算量分析
对于有n条边的凸多边形,本算法最多需要进行[(n-1)/2]次与分割线的比较和3次与凸多边形边的比较。当多边形顶点个数为4时,本算法具有最差的时间复杂度O(n),当顶点个数增加时,算法性能将得到提升。对于某些点,本算法只需要3次计算就可以确定待测点的位置,因此本算法最优时间复杂度为O(1)。因此,本算法平均时间复杂度为O(n/2)。
而使用射线法进行内外点检测时,必须将待测点与多边形的每一条边进行比较才能确定该点是否在多边形内,即射线法时间复杂度始终为O(n)。因此,对于指定的凸多边形,待测点个数越多,本算法相对于射线法节省的时间也就越多。
4 实验与分析
本文使用Visual Studio 2013对本算法以及射线法进行了比较。测试计算机配置Intel(R)Core(TM)i7-4870HQ的CPU、16GB内存和Windows7 x64操作系统。
1)测试凸多边形顶点个数与算法耗时的关系
实验使用10 000个随机待测点分别对顶点个数为10、20、30、40、50的凸多边形进行了内外点的测试,顶点个数与算法耗时关系见图3。顶点个数与算法耗时比较表,见表1。
实验证明,当凸多边形具有相同顶点个数时,本算法性能明显优于射线法。当多边形顶点个数较少时,算法优势不明显。这是因为当多边形顶点个数较少时,本算法不仅需要与分割线进行比较,还需要与三角形区域的三条边进行比较[14]。例如,当凸多边形只有4个顶点时,本算法性能达到最差,即需要进行1次与分割线的比较,和3次与边的比较,与射线法一样共需4次比较。因此,顶点个数越多,本算法性能越好。
2)测试待测点个数与算法耗时的关系
实验分别使用10 000到60 000个随机待测点对顶点个数为10的凸多边形进行了内外点的测试,待测点个数与算法耗时关系见图4。待测点个数与算法耗时比较表,见表2。

图3 顶点个数与算法耗时关系

表1 顶点个数与算法耗时比较

图4 待测点个数与算法耗时关系
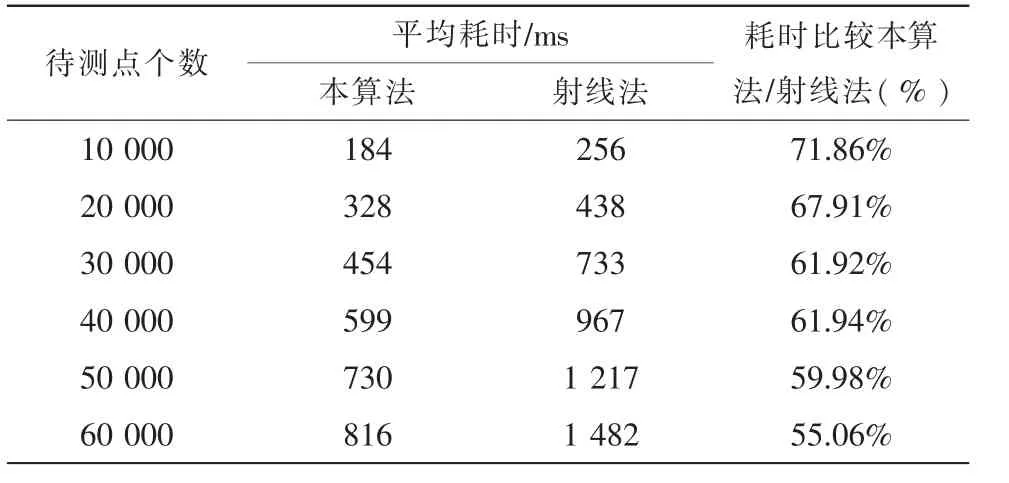
表2 待测点个数与算法耗时比较
实验证明,待测点个数越多本算法性能越好,相对于射线法节省的时间也越多。由表2可以看出,当待测点个数线性增加时,本算法相对于射线法的耗时并不是线性减少,这是因为待测点的分布具有随机性。
5 结 论
本文提供了一种简单有效的凸多边形内外点判定算法,它不需要对凸多边形进行预处理,节省了大量预处理的时间消耗。本算法使用顶点向量对凸多边形的顶点进行管理,并使用二分法递归的分割凸多边形,将待测点与凸多边形的位置关系转化为待测点与三角形的位置关系。由于使用了分割法,本算法不仅可以判定待测点是否在多边形内,还能给出待测点的三角形区域,并且顶点个数越多,划分的区域就越精确。
本算法时间复杂度在O(1)到O(n)之间,而平均时间复杂度为O(n/2)。因此与射线法相比,本算法在大多数情况下均可以节约20%~50%的算法耗时,实验结果表明,本算法易于实现,高效稳定。
[1]周欣,张树有,潘志庚.基于链码和特征形的多边形内外点判断算法 [J].计算机辅助设计与图形学学报,2006,18 (9):1317-1321.
[2]张宁宁,张树有,谭建荣.映射相关边概念的多边形内外点判别算法 [J].计算机辅助设计与图形学学报,2004,16 (7):935-938.
[3]李静,王文成.基于网格中心点的点在多边形内的高效判定[J].软件学报,2012,23(9):2481-2488.
[4]肖飞.基于点序的多边形分割方法探讨[J].信息技术与信息化,2012(5):100-102,105.
[5]赵海森,杨承磊,吕琳.多边形中的点可见性快速算法[J].计算机辅助设计与图形学学报,2013,25(3):331-340.
[6]杨玉婷,康厚良.2D图形引擎中的平面多边形内外点判别[J].图学学报,2013,34(3):100-105.
[7]高天豪,王文成,朱滨海.基于凸片段分解和格网的点在多边形中的可见边检测 [J].计算机辅助设计与图形学学报,2013,25(8):1114-1120.
[8]向俊,王静,夏幼明.判断点与多边形拓扑关系的改进算法[J].计算机工程与设计,2014,35(5):1732-1737.
[9]杨雅军,段明义.判断点与指定多边形区域的关系的改进算法[J].电脑知识与技术,2014,10(22):5362-5364.
[10]翟艳,徐卫亚,张强.点与多边形或多面体的拓扑关系判断[J].计算机工程与设计,2015,36(4):972-976.
[11]王鹏飞.四边形阻抗原理应用中出现的问题及解决办法[J].陕西电力,2011(8):79-81,89.
[12]施先旺,刘婷婷,李国良.采用有限状态机实现控制指令的可靠检测[J].火箭推进,2011(5):63-68.
[13]赵志伟,陈学有,潘琼.采用特征值法和Prony法相结合的PSS自适应控制[J].陕西电力,2012(6):49-52,62.
[14]张伟,陈锋,马军强,等.轨/姿控发动机脉冲后效冲量快速算法的研究及应用[J].火箭推进,2012(1):51-56.
Point inclusion test method based on dichotomy
YU Kai,YU Meng-hong
(College of Computer Science and Engineering,Jiangsu University of Science and Technology,Zhenjiang 212003,China)
Point inclusion test is a basic algorithm of computer graphics,it's purpose is to determine whether a test point is in the specific polygon.Traditional ray-crossing method and angle algorithm have relative low efficiency,their average time complexity are O(n).So,if a polygon has a great many edges or test points,these algorithms will take much more time.This paper analyses the shortcomings of traditional ray-crossing method and angle algorithm,then proposes an efficient point-inpolygon test method based on dichotomy.At last,this paper uses many experiments to show that the average time complexity of this algorithm is O(n/2).By partitioning convex polygon recursively and judging the relative position between points and the line,this method eventually translate this problem into judging the relative position between triangle and points.Compared with the classic algorithms,such as the ray crossing method or the angle algorithm,this algorithm not only have the advantage rapid and stable,also can give which triangle region the points locate in.
convex polygon;dichotomy;include testing;recursive partitioning
TN0
A
1674-6236(2016)16-0187-04
2015-09-06稿件编号:201509043
于 凯(1989—),男,江苏徐州人,硕士研究生。研究方向:模式识别与智能系统,图像处理。
