基于边失效的舰艇装备保障网络抗毁性分析*

张　肖　戴明强　邵　帅

(海军工程大学理学院　武汉　430033)

ZHANG Xiao　DAI Mingqiang　SHAO Shuai

(College of Science, Naval University of Engineering, Wuhan　430033)



基于边失效的舰艇装备保障网络抗毁性分析*

张肖戴明强邵帅

(海军工程大学理学院武汉430033)

舰艇装备保障网络是一个包含了不同种类节点和错综复杂路线的复杂系统，实施保障计划的过程中总会碰到道路故障和拥堵的情况，即边失效。针对这一问题，分析边失效时负载的分流机制，取网络的繁忙程度和网络的复杂程度两个因素对网络级联效应抗毁性的影响进行研究，并构建模拟网络模型进行仿真实验。结果表明，网络越繁忙，网络复杂程度越低，网络级联失效抗毁性越差；而网络复杂程度比繁忙程度对抗毁性的意义更大。

舰艇装备保障； 边失效； 级联失效； 网络抗毁性

ZHANG XiaoDAI MingqiangSHAO Shuai

(College of Science, Naval University of Engineering, Wuhan430033)

Class NumberE273

1　引言

舰艇装备保障网络一般位于局部沿海、相对陆上其他保障网络较小的区域内，是主要提供海军舰艇的装备保障功能的物流网络。在网络日常运行中，在较短的时间内通过节点和边的负载变化很小，影响保障网络级联失效抗毁性的更重要的因素是网络的节点容量分布与边的流量分配。一般舰艇需要对装备进行保障的时间通常是在出航前或者是完成相关任务返港后。而在出航前根据任务需要，有不同的备战备航等级，相应的时间要求也是有长有短。也有在返港之后根据需要马上去执行下一个任务的时候，而在航行时造成的装备损耗则需要在这两次任务的间隙进行装备保障。这说明舰艇装备保障任务具有很强的应急性，对保障的速度提出了较高的要求。在道路出现损毁、拥塞(边失效)时必然会影响保障的速度；当运输的装备为舰艇出航所必须时，会使整个作战计划延后，延误战机。

目前对于在装备保障的运输环节中出现中断和延迟所引发的级联失效对保障网络抗毁性影响的研究还处于起步阶段，相关研究不多。文献[1～5]在物流网络节点或边失效时，采用基于无向物理网络进行随机比例分流的方法，对负载进行重新分流转移。这对实际装备保障环境下的方向性选择缺乏考虑。另外，一些级联失效模型假设失效节点间的边链接是可移除的[5]。以上两点均与实际保障特征有所出入，例如装备运输过程中在遭遇交通堵塞或其他事故的发生后，不仅存在装备分流转运的方向选择问题，且发生事故的道路也并非就此完全作废，在现场道路运输载体上的装备也不可能放弃不用。显然，这些实际环境因素对于物流网络中的级联失效传播有着不容忽视的影响，因此需要针对符合物流网络中自身特征的级联失效模型进行构建。

2　边失效引发级联失效的分析

研究发现，网络中越是负载能力较大的路段或链接边，其上的流量往往也越大。而随着生产力的发展，现代交通工具也开始了爆炸式的发展。由于部分路段受到负载能力的限制，在核心路段几乎每天都会发生拥堵。它们较其他路段或边在突发或干扰事件下更易产生运输中断。本文选取物流局部网络结构如图1所示，假设其中任意选取的边eij突发中断继而失效。考虑到现实物流运输网络中的边失效后的不可移除性，本文以下所假设物流交通运输中断导致的边失效只是表征运输线路服务功能的暂时性中断。

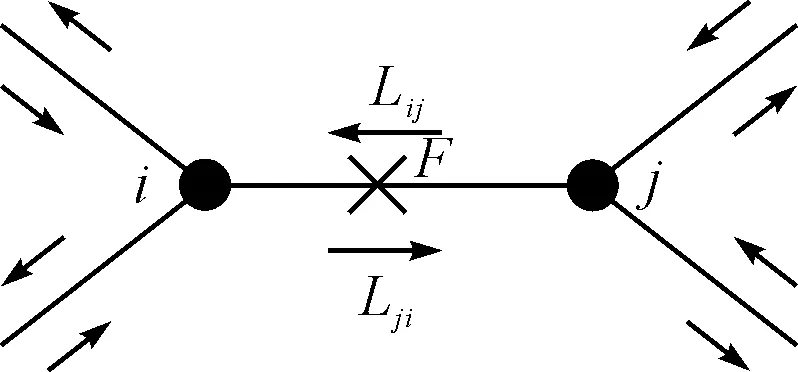
图1　运输中断的局部网络示意图

边eij在F处发生中断而失效，在整个ij段上的物流负载会通过如下形式发生转移，如图2所示。

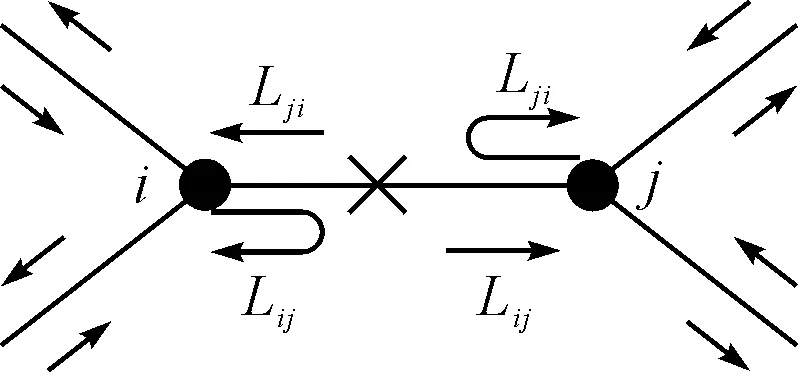
图2　运输中断时负载的流向图

1)沿着既定的方向已通过F点的负载物流则按原计划继续运输至后续节点和边。

2)未通过F点的负载物流则原路返回，通过其他的路径来继续完成任务。

3　装备保障网络级联边失效模型的构建

3.1网络参数的选取

根据上一小节的分析，易知失效边(运输中断所在路段)的邻接边(关联路段)在网络中的负载能力大小和重要性程度对物流运输中断后的失效负载分配传递具有主要影响。网络的复杂性、连通性也对保障任务的物流能否到达目的地有着重要影响。

首先仍然采用介数来定义物流网络中的运输路段的重要性[6～7]：

(1)

其中，Be为任意边e的介数，σgh表示为任意节点g和h之间的最短路径的总数，σgh(e)表示任意节点g和h之间的所有最短路径中途径边e的路径数量。该定义以物流保障任务经过该路段的次数作为路段重要性的体现，很符合实际物流保障运作特征。

其次，考虑到既有的大多数研究釆用边的两端节点的度来对边(运输路段)的负载能力进行量化[8,9]，缺乏考虑边(运输路段)自身属性在网络中的重要度。另外，也不是两端节点的每条边都能最终链接到保障任务的目的地；如图3所示，节点AB之间的边发生中断，返回节点B的负载LBA可以通过边eBD到达节点D，进而到达保障任务的目的地E。而节点B与节点C之间的边eBC则在此次任务中无法担任分流边。

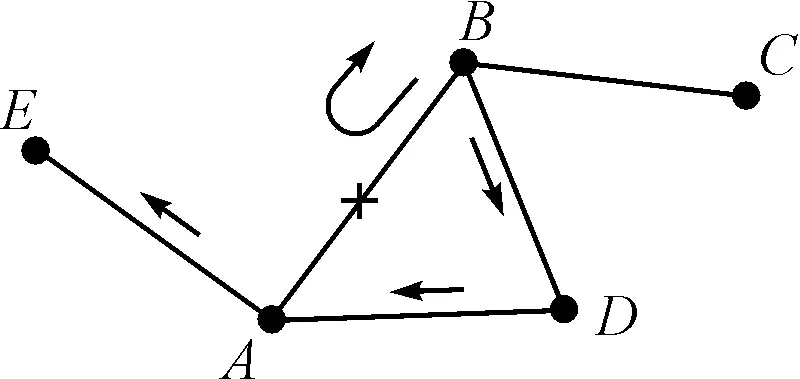
图3　针对任务需求的分流边

为此，本文在既有研究的基础上加以考虑边的介数因素，给出如下关于边(运输路段)负载能力的定义：假设任意边e的负载能力Ce，具体计算如式(2)所示：

Ce=Be(kikj)θ

(2)

其中，ki和kj分别为边(运输路段)两端节点i和j的度。

网络的平均度〈k〉则能较好地反映一个网络的复杂性和连通性。〈k〉值越大，网络的连通性越好，执行保障任务的物流就更大可能到达原计划目的地。〈k〉值的具体计算公式如下：

(3)

3.2分流机制

在不考虑运输方向的情况下，失效边e上的负载Le将根据邻接边在网络中的重要度大小进行分配流量。其中，设任意的关联邻接边eix获得的失效边的上的负载分配比例大小为pix其具体计算方式如式(4)所示：

(4)

其中，Γij为失效边e的邻接边集合。

3.3模型评价指标的确立

釆用边的损失比例R作为网络级联失效后的抗毁性评估指标，其计算方法具体如式(5)所示：

(5)

其中，NE为网络的边的数量，Nf为失效边的数量。R的取值范围为(0,1]。该指标值越大，说明突发事件级联失效对网络的破坏性越大。

4　仿真实验

4.1实验网络模型

通过Matlab软件生成节点规模为N=100的BA网络来模拟物理网络结构模型，其中边的数量为393条。运用ucinet软件得到实验网络拓扑结构体如图4所示，图中节点形状的大小对应着节点度的大小。为不失一般性，让节点的规模不变，将边的数量分别随机降至317、275、227，此时平均度〈k〉也分别降至6.3、5.5、4.5，之后与平均度〈k〉为7.8的网络进行比对研究。

图4　节点数为100的BA网络

通过对该网络的节点度分布状况进行分析统计，如图5所示，其中图中横坐标表示节点的度k，纵坐标为k的分布统计函数P(k)，表示度为k的节点所占的比例。该网络模型具有度分布不均匀的网络特性。

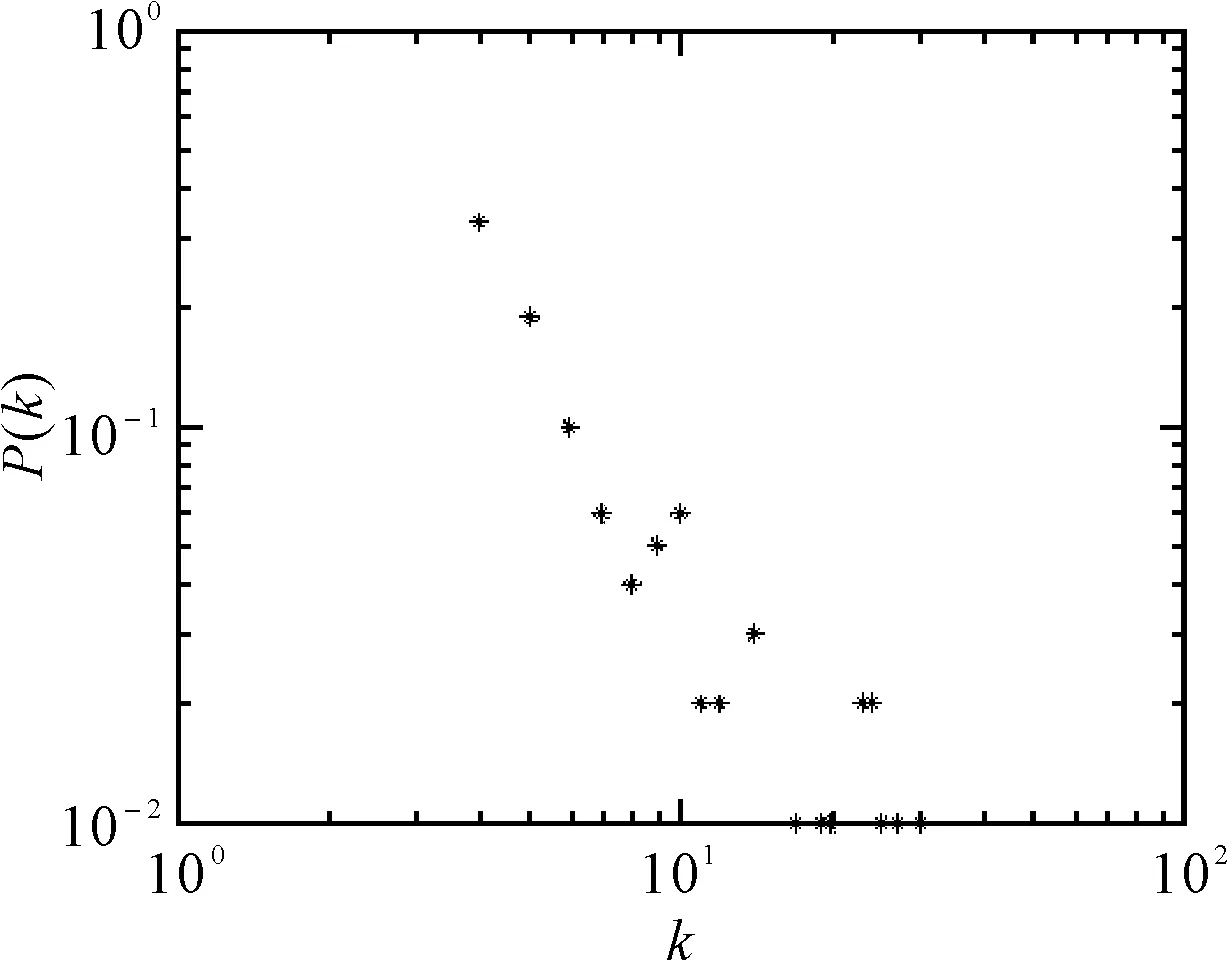
图5　节点度分布

通常边的负载与其容量成正比。边的容量越大，经过边的负载才能越大。即负载与容量呈正相关性。用数学表达式表示它们的关系为式(6)：

Lij(0)=μCijμ∈[0,1]

(6)

其中，Lij(0)为任意边eij的初始负载。μ为控制参数，体现出负载占当前边的总容量比，也表征了本路段的繁忙程度。而失效点F与失效边eij两端的空间距离的比值D∂F/Dij，由于失效点发生的随机性，在这里以随机数ε来替代这个比值，且ε∈[0,1]。

4.2算法分析

根据上节建立的保障网络级联失效模型及其分析，这里给出该模型的算法：

1)网络初始正常状态下，任意物流边(运输路段)Dod的负载为Lij，负载能力为Cij，i,j=1,2,…,N。

2)初始时刻，随机选择任意边(运输路段)eij，令其突发失效。

3)根据未失效前的网络邻接矩阵A中非零元素aij及物流逻辑网络方向量化矩阵Dod判断获得失效边eij的关联邻接边集合Γij，由失效负载分流规则即式(4)进行失效负载的分配转移。

4)根据节点失效传播函数判断关联邻接边eij是否崩溃失效；若失效，返回步骤2)。

5)直到再无边(运输路段)崩溃失效的发生，结束。

4.3实验结果分析

先对平均度〈k〉为7.8，边数为393的网络进行实验，取μ=0.8，步长M=0.02，得到控制参数μ与损失比例R的关系如图6。

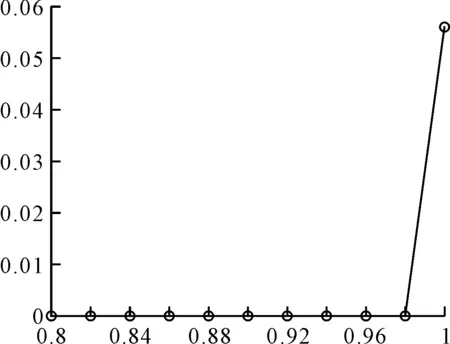
图6　控制参数μ与损失比例R关系图

图6中坐标轴的横轴表示控制参数μ，纵轴表示损失比例，由图可知，在网络足够复杂、平均度〈k〉足够大时，即使是98%的高负荷的运行，网络中有单个边出现失效时是不会发生级联效应的，因为网络规模够大的话，一条边的流量相对来说就比较小了所以不会造成损毁级联效应。

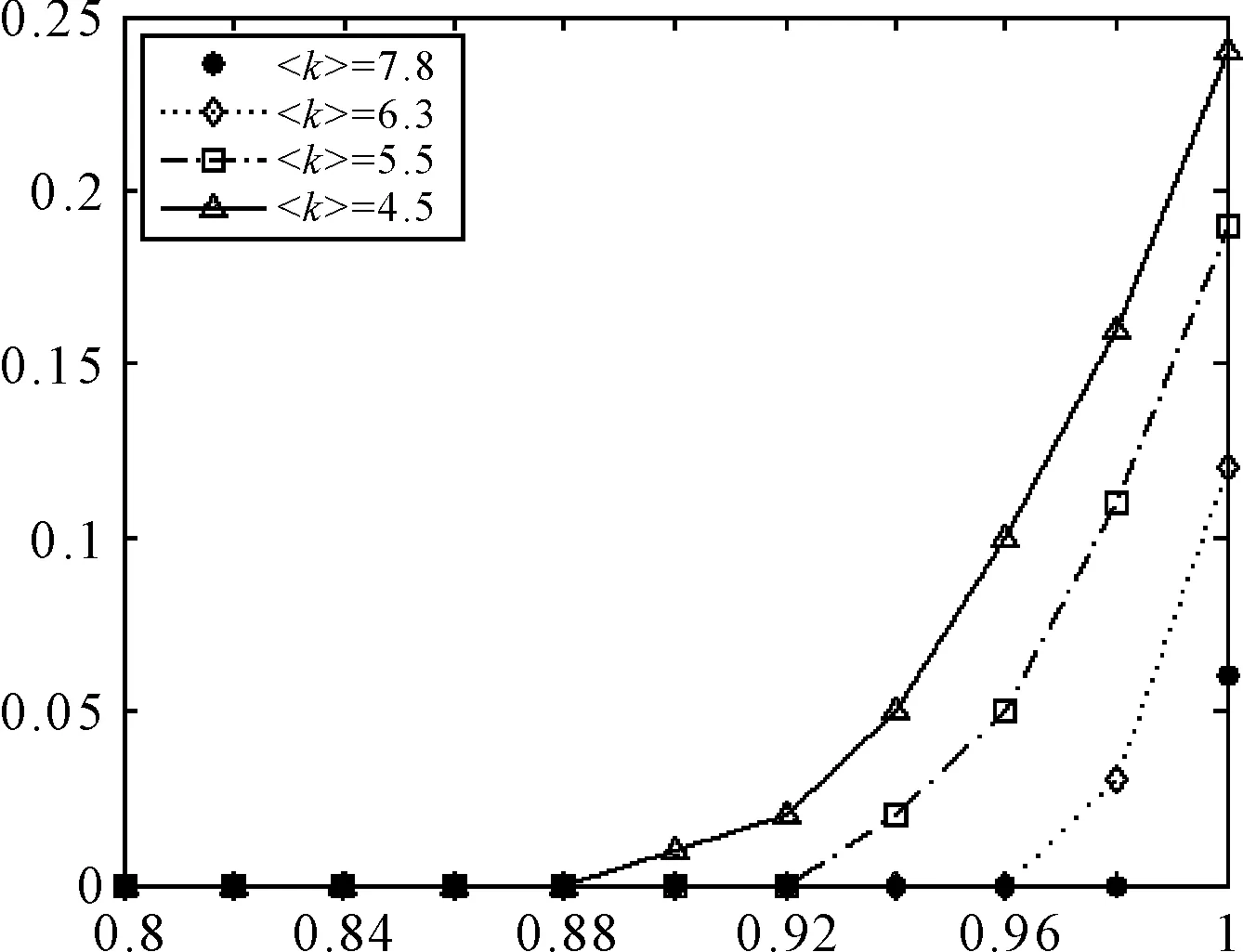
图7　不同〈k〉值网络仿真结果分析图

平均度〈k〉减少为6.3、5.5、4.5后得到控制参数μ与损失比例R的关系随〈k〉变化而变化，如图7所示。随着平均度〈k〉的减小，控制参数μ每增长一个步长，损失比例R会增加。综合图6和图7可知，平均度〈k〉对网络抗毁性所作的贡献比控制参数μ的大。也就是说，对于网络级联失效抗毁性来说，网络中互连边的数量多少，比边的负载率更加有意义。即在不考虑装备保障物流其他指标(如驾驶员水平、路况)的情况下，不怕道路的通行率高，就怕可选择的路不多。

5　结语

本文以舰艇装备保障网络为研究对象，对网络中边失效所引发的级联失效进行分析，提出失效边上的负载的分流机制，选取边的介数以及网络的平均度为仿真模型的参数，确立了网络模型的评价指标。

运用Matlab软件进行了一系列仿真实验，实验结果表明，控制参数μ与平均度〈k〉均能影响网络级联效应性。其中，平均度〈k〉对网络抗毁性所作的贡献比控制参数μ的要更大。即网络中有更多的互连边、网络的复杂性更高，网络级联效应抗毁性越好。

[1] 王建,刘衍珩,梅芳,等.基于网络拥塞的Internet级联故障建模[J].计算机研究与发展,2010,47(5):772-779.

[2] 崔晓迪,穆东,王耀球.基于客户需求的物流业务耦合系统的研究[J].北京交通大学学报,2008,7(2):42-47.

[3] Schöfer M, Scholz J, Greiner M. Proactive Robustness Control of Heterogeneously Loaded Networks[J]. Phys. Rev. Lett.,2006,96(10):108-701.

[4] Li K, Gao Z, Mao B, A weighted network model for railway traffic[J]. International Journal of Modern Physics C,2006,17(9):1339-1347.

[5] Sen P, Dasgupta S, Chatterjee A, et al. Small-world properties of the Indian railway network[J]. Physical Review E Phys Rev E,2003,67(3):036106.

[6] 王建.现代物流网络系统的构建[M].北京:科学出版社,2005.

[7] 种鹏云,帅斌,陈钢铁.恐怖袭击下危险品运输网络级联失效抗毁性建模与仿真[J].计算机应用研究,2013,30(1):107-110.

[8] Zheng, D.F. and Ergön G.. Coupled growing networks[J]. Advances in complex systems,2003,6(4):507-514.

[9] 王建伟,荣莉莉.基于负荷局域择优重新分配原则的复杂网络上的相继故障[J].物理学报,2009,58(6):3714-3721.

[10] Wang W X, Chen G. Universal robustness characteristic of weighted networks against cascading failure[J]. Physical review. E,2008,77(2):026101.

[11] 黄英艺.考虑级联失效的物流网络抗毁性研究[D].大连：大连理工大学,2014.

Analysis of Network Security Survivability of Warship Equipment Based on Edge Failure*

Warship equipment support network is a complex system which contains different kinds of nodes and complex routes. In the process of implementing the supporting plan, there will always be a road failure and congestion. Aimed at this problem, the edge failure load diversion mechanism, taking two factors including: the complexity of the network busy degree and network to network cascading invulnerability, and the simulation model is built to simulate the network. When complex network degree is lower and more busy, the network cascade failure survivability is worse. For network survivability, network complexity has a greater significance than network busy level.

warship equipment support, edge failure, cascading failure, network invulnerability

2016年2月10日,

2016年3月24日

张肖,男,硕士研究生，研究方向：军事系统建模与运筹决策。

E273

10.3969/j.issn.1672-9730.2016.08.010