改进电磁暂态仿真中数值振荡消除方法的研究

解笑苏，王　帆，张学凯（.国网山东省电力公司电力科学研究院，济南　5000；.国网山东省电力公司济南供电公司，济南　500；.国网山东省电力公司，济南　5000）

·专题论述·

改进电磁暂态仿真中数值振荡消除方法的研究

解笑苏1，王帆2，张学凯3
（1.国网山东省电力公司电力科学研究院，济南250003；2.国网山东省电力公司济南供电公司，济南250012；3.国网山东省电力公司，济南250001）

在不采取任何修正措施的情况下，电磁暂态仿真计算在开关动作时可能会出现数值振荡现象。目前，线性插值法是消除这种振荡最常用的方法。但是，如果插值法采用的初始数值存在误差，数值震荡可能无法被完全消除。提出一种改进的线性插值法，通过调整计算方法排除误差影响来解决这一问题，并通过仿真对结果进行了验证。

电磁暂态仿真；数值震荡；线性插值

0　Introduction

Electromagnetic transient simulation has characteristics of accurate phenomenon portray and good numerical stability，and thus plays a key role in power system design and planning，analysis and operating control，online dynamic security assessment and so on.As a result of the trapezoidalmethod's own flaw，the computing process has a risk of numerical oscillation at the same time of switches action when nomeasures are taken［1］.

The CDA method［2-4］was firstly used to solve the problem.This method uses 2 steps of the backward Euler method to replace the trapezoidal method when switches act，and it performs well without using the value before changes happen.But facing themore and more complex simulation models such as power electronic devices，its complication and low efficiency expose.

The linear interpolation method replaced the CDA methodbecauseofthehigherefficiencyand flexibility［5-9］. As the simulating step of integration is small enough，the part of curve between two points can be regarded as a straight line approximately，and any points in this part can be calculated according to this line.This method provides a shortcut for calculating any point in range of one step and eliminating numerical oscillations.

The existing linear interpolationmethod has a defect that the oscillation may not be eliminated when error existing in the calculation progress.Although this case may not happen at usual time，it does have a big in-fluence on the simulation result.

1Generation of NumericalOscillation

The numerical oscillation is caused by the sudden change of non-state variables when the state variables crossing zero，owing to the defect of trapezoidal method.

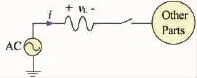
Figure1　A Simple System

Figure 1 shows a simple system as an example.If the switch breaks at t=1，i and vLshould change along the real line in Figure 2.

Figure 2　Cause of NumericalOscillation

Butusing the trapezoidalmethod，we can get

Aswe know，when t≥2，i（t）=i（t-1）=0.And then we can get

As a result，the wave of vLbecomes the dotted line in Figure 2（b），and the numerical oscillation arises.

2　The Defectof Linear Interpolation Method

The steps of the linear interpolationmethod to eliminate numerical oscillation are as follows：

1）Calculate the unmodified result of t=2 using the trapezoidalmethod based on the result of t=1；

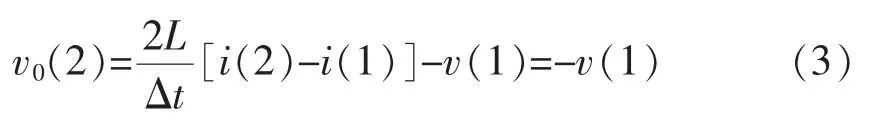
2）Calculate the result of t=1.5 using the interpolationmethod based on the resultof t=1 and the unmodified result of t=2；

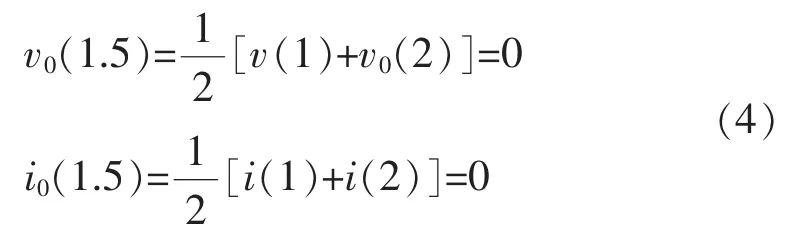
3）Calculate the result of t=2.5 using the trapezoidalmethod based on the result of t=1.5；

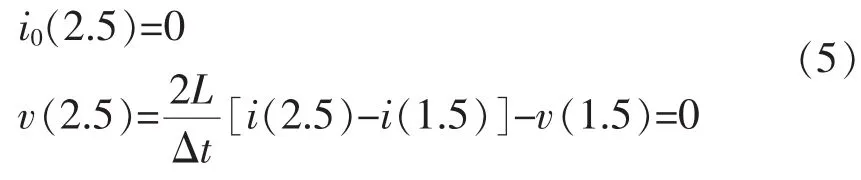
4）Calculate the modified result of t=2 using the interpolation method based on the result of t=1.5 and t=2.5；

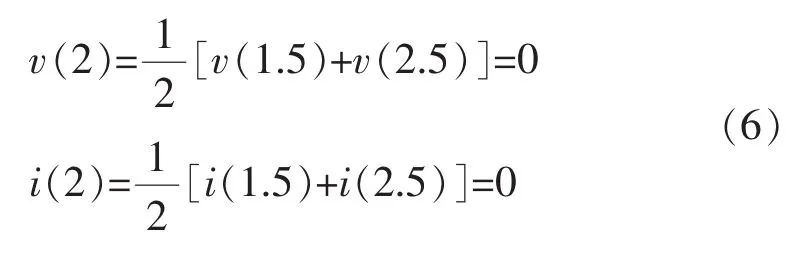
Generally，thismethod is correct and efficient，but the result may be as Figure 3 when error existing in the result of t=1.

Figure 3　The result of interpolation method when error existing

Assuming thatwemade amistake of i（1）=Δi not 0，the unmodified result should be

Using the linear interpolationmethod，we can get

According to the trapezoidal method and the linear interpolationmethod，we can get

Themodified v（3）≠0，and i（3）=0.Ifwe continue the calculation，we will get v（4）=-v（3）and v（5）=v （3）… .The numerical oscillation will never be eliminated.

3　The Improved Linear Interpolation Method

Facing the defect above，the numerical oscillation will be easily eliminated if we just change the order of calculation as follows:

1）Calculate the unmodified result of t=2 using the trapezoidalmethod based on the result of t=1；

2）Calculate the result of t=1.5 using the interpolationmethod based on the result of t=1 and the unmodified result of t=2；

3）Calculate the unmodified result of t=3 using the trapezoidal method based on the unmodified result of t=2；

4）Calculate themodified result of t=2.5 using the interpolationmethod based on the unmodified result of t=2 and t=3；

5）Calculate the modified result of t=2 using the interpolation method based on the result of t=1.5 and t=2.5；

As same as the assumption above，we can get the same resultas Equation（7）and Equation（8）.And according to the trapezoidal method and the improved method，we can calculate

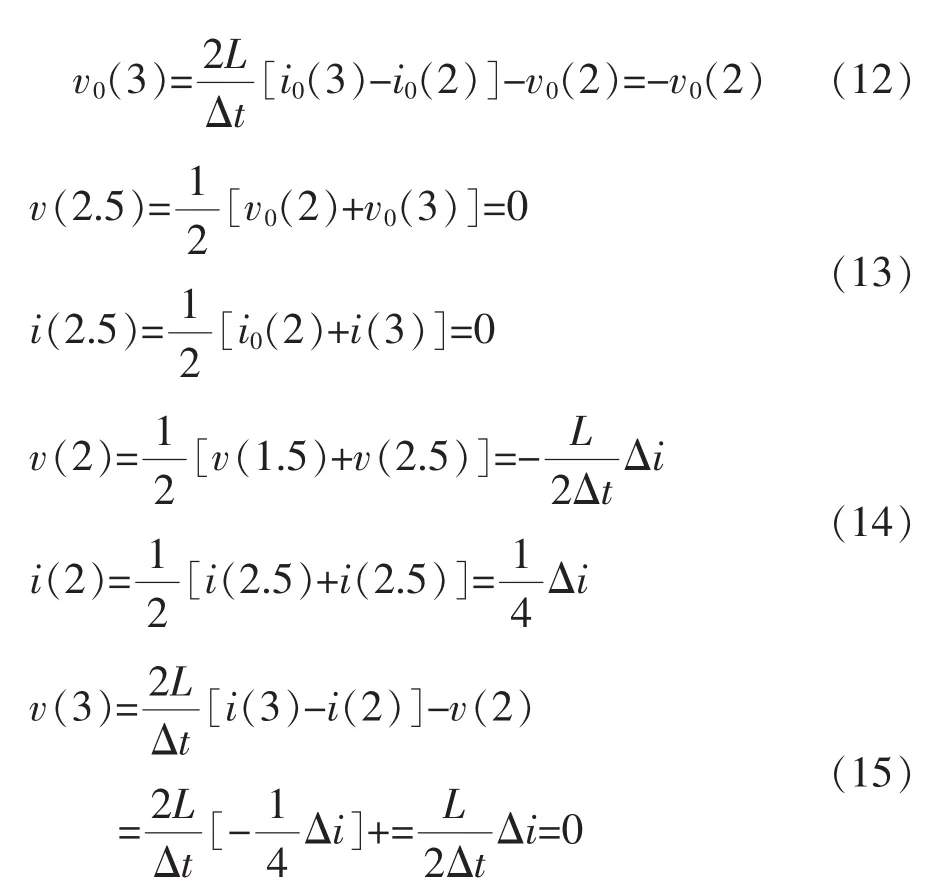
Themodified v（3）=0，and i（3）=0，the numerical oscillation is eliminated.The simulation results comparison of the twomethods is as Figure 4.

Figure 4　The resultof new method when error existing

4　Conclusions

The existing linear interpolation method may not be efficient in eliminating the numerical oscillation when error existing in the calculation progress.We provide an improved linear interpolation method，and prove its correctness in frontof errors.

Reference

［1］H.W.Dommel.EMTP Theory Book［M］.Beijing，China：Water Resources and Electric Power Press，1991.

［2］J.R.Marti，J.Lin.Suppression of Numerical Oscillations in theEMTP［J］.IEEE Transaction on Power Systems，1989，4（2）：739-747.

［3］J.M.Lin，J.R.Marti.Implementation of the CDA Procedure in the EMTP［J］.IEEE Trans.Power Systems，1990，5（2）：394-402.

［4］Wang Chengshan，Li Peng，Wang Liwei.Research Progress of Electromagnetic Transient Simulation for Power Systems［J］.Automation of Electric Power Systems，2009，33（10）：97-103.

［5］P.Kuffel，K.Kent，G.Irwin.The Implementation and Effectiveness of Linear Interpolation within Digital Simulation［J］.Electrical Power and Energy System，1997，19（4）：221-227.

［6］A.M.Gole.Electromagnetic transient simulation of power electronic equipment in power systems：challenges and solutions. Power Engineering Society General Meeting，2006，Montreal，Canada.

［7］Zou Ming，Mahseredjian Jean，Joos Geza，et al.Interpolation and Reinitialization in Time-domain Simulation of Power Electronics Circuits［J］.Electric Power Systems Research，2006，76 （8）：688-694.

［8］Wang Chengshan，Li Peng，Huang Bibin，et al.An Interpolation Algorithm for Time-Domain Simulation of Power Electronics Circuit Considering Multiple Switching Events［J］.Transactions of China Electrotechnical Society，2010，25（6）：84-88.

［9］Liu Tao，Yan Yipeng，Jin Na，et al.Interpolation Algorithm for ElectromagneticTransientSimulationConsideringMultiple Switching Events［J］.Proceedings of the CSU-EPSA，2013，25 （6）：144-147.

Accepted date：2016-03-09

Xie Xiaosu（1987），received master degree in Engineering from North China Electric Power University in 2013.He is now working in State Grid Shandong Electric Power Research Institute.His main research interest is generator excitation.

Im proved Numerical Oscillation Elim ination M ethod in Electromagnetic Transient Simulation

XIE Xiaosu1，WANG Fan2，ZHANG Xuekai3
（1.State Grid Shandong Electric Power Research Institute，Jinan 250003，China；2.State Grid Jinan Power Supply Company，Jinan 250012，China；3.State Grid Shandong Electric Power Company，Jinan 250001，China）

Electromagnetic transient simulation has a risk of numerical oscillation at the same time of switches action when no measure is taken.The linear interpolation method ismostwidely used to eliminate the numerical oscillation at present.But in the case of error existing in the initial value，the numerical oscillation may not be eliminated completely.We put forward an improved method of linear interpolation by adjusting the calculation method to eliminate the influence of errors to solve this problem，and prove the results through simulation.

electromagnetic transient simulation；numerical oscillation；linear interpolation

TM744

A

1007－9904（2016）04－0026－03