基于压缩感知和分段正交匹配追踪StOMP算法的优化
2016-09-08李娣娜邵思飞
黄 同,李娣娜,邵思飞,2
(1.延安大学 西安创新学院,陕西 西安710100;2.延安大学 物理与电子信息学院,陕西 延安 716000)
基于压缩感知和分段正交匹配追踪StOMP算法的优化
黄 同1,李娣娜1,邵思飞1,2
(1.延安大学 西安创新学院,陕西 西安710100;2.延安大学 物理与电子信息学院,陕西 延安 716000)
在分析分段正交匹配追踪StOMP算法迭代过程中多原子匹配方法的基础上,为了进一步减少算法迭代次数,提高重构精度,提出了基于互相关向量的自适应极限因子选取和迭代结束条件重设的优化方法。通过MATLAB编程实验,在随机给定稀疏度为K的测试数据条件下,优化后的算法较StOMP算法迭代次数减少1-2次,重构精度提升约1%,鲁棒性增加,而运行时间开销相差无几。
压缩感知;正交匹配追踪算法;分段正交匹配追踪算法;StOMP
在基于奈奎斯特采样定理的传统信号处理体系中,信号必须首先采样,然后进行压缩等后续处理。采样数据往往非常庞大,但大量数据相关性很高,造成资源的极大浪费。压缩感知(Compressed Sensing,CS)理论指出,如果信号是稀疏的或者在某个基下可稀疏化,那么用少量的观测值就可以保持信号的结构和相关信息,这样用于精确重构信号的采样数量可以极大降低,相当于压缩和采样同步完成。正交匹配追踪算法(Orthogonal Matching Pursuit algorithm,OMP)作为重构算法之一,因计算复杂度低,重建速度快得到了广泛应用,但信号重建质量有待提高,为此,人们提出了很多改进算法,文中在分段正交匹配追踪算法(Segmented Orthogonal Matching Pursuit algorithm,StOMP)的基础上通过实验,提出进一步的改进思路。
1 压缩感知理论
压缩感知基于信号的稀疏性,以远低于奈奎斯特采样率的速率对信号进行非自适应的测量采集。稀疏分解、随机测量和重构算法是压缩感知的3个关键[1],稀疏分解和随机测量属于信号的压缩,重构算法是它的逆过程,相当于解压缩,与稀疏分解方法和随机测量矩阵直接相关。
信号的在稀疏基Ψ上的稀疏分解是压缩感知应用的基础,除了离散余弦变换、离散傅里叶变换、离散小波变换等经典的稀疏化方法外,冗余字典下的稀疏分解逐渐成为新的热点。冗余字典是过完备的,字典中的冗余函数称为原子,它用原子取代了基函数。
测量矩阵Φ′(M×N M<N)是随机测量的关键,既直接影响正向压缩,也影响反向重构。在将原非稀疏信号X(N×1)进行稀疏分解,得到稀疏系数X′(N×1)后,需要通过矩阵乘法的形式采样得到M个观测值Y,并保证能重构出稀疏基Ψ下等价的稀疏系数向量X′或者长度为N的信号X。鉴于此,测量矩阵的构造必须遵循一定的法则,具备一定的特性。Candès提出的约束等距性(Restricted Isometry Property,RIP)指出,要想使信号完全重构,必须保证测量矩阵不会把两个不同的稀疏度为K的信号映射到同一个采样集合中[2]。Donoho也从定性和定量的角度给出测量矩阵要满足3个特性[3]:1)由测量矩阵的列向量组成的子矩阵的最小奇异值必须大于一定的常数;2)测量矩阵的列向量体现某种类似噪声的独立随机性;3)满足稀疏度的解是满足1范数最小的向量。目前,常用的测量矩阵主要有高斯随机矩阵、伯努利矩阵、傅立叶随机矩阵、哈达玛矩阵和一致球矩阵等。
重构算法是恢复原始信号的必需过程。从数学上讲,信号重建问题就是寻找欠定方程组的最简单解的问题,目前压缩感知的重构算法主要包括贪婪算法和凸优化算法两大类。贪婪算法[4]主要包括匹配追踪算法、正交匹配追踪算法、分段正交匹配追踪算法、补空间匹配追踪算法等,它们的本质是通过反复的递归过程,实现信号的最佳逼近。凸优化算法[5]主要包括梯度投影法、基追踪法、最小角度回归法等,它们的本质是把0范数放宽到1范数通过线性规划求解。贪婪算法计算复杂度低,重建速度快,但是信号重建质量有待提高;凸优化算法信号重建质量较高,但是计算复杂度高,重建速度慢。
2 分段正交匹配追踪算法及其优化
2.1正交匹配追踪算法OMP
正交匹配追踪算法和匹配追踪算法 (Matching Pursuit algorithm,MP)总体类似,它是在每一次的迭代过程中,从冗余字典(即感知矩阵Φ)里选择与信号最匹配的原子(列),经过Gram-Schmidt正交化后,再将信号在这些正交原子构成的空间上投影,得到信号在各个已选原子上的分量和余量,然后采用相同方法,经过数次迭代选出与信号各次余量最为匹配的原子,所选原子均需要满足一定条件,余量随着分解过程迅速减小直至迭代结束[6]。由于递归过程中对己选原子集进行了正交化,保证了迭代的最优性,相比匹配追踪算法,减少迭代次数,收敛效果更好。
正交匹配追踪算法以贪婪迭代的方法选择Φ的列,使得在每次迭代中所选择的列与当前的冗余向量最大程度地相关,从测量向量中减去相关部分并反复迭代,直到迭代次数达到稀疏度K,迭代停止。
2.2分段正交匹配追踪StOMP算法及其优化
正交匹配追踪方法利用Gram-Schmidt正交化过程将投影方向正交化,从而提高了追踪的效率,但是其正交化过程引入了新的计算开销,特别是对于图像信号,计算量仍然巨大。2006年Donoho进一步提出了每次匹配追踪时选出的是多个匹配原子而不是单个原子的分段正交匹配追踪算法[7],该算法将OMP算法进行一定程度的简化,降低了稀疏分解精度,提高了计算速度。
设Φ={gr}r∈Θ是由Θ个(Θ>N)范数为1的向量构成的冗余字典。该字典包含N个线性无关的向量,这N个向量构成长度为N的信号空间CN的一个基。设f为待处理信号,m为第次迭代(即当前迭代次数),为余量,为极限因子。初始时m=0,下标集合Im=I0=φ。
分段正交匹配追踪算法的单次迭代过程是:首先,m=m+ 1,通过内积运算,将投影到Θ的每一个向量gr∈Θ上,引入极限因子tm,找到满足极限因子条件的原子的下标集Im={i:≥tm,r∈Θ},也即得到了满足条件的所有原子;其次,与上一次迭代得到了原子下标集合Im-1合并,从而更新所选的原子下标集合Im=Im∪Im-1;然后,利用Gram-Schmidt正交化方法将这组原子正交化,并定义正交化后的向量为ui:ui=grup,i∈Im;再然后,将余项投影到ui(i∈Im)上,得到,由于由新的余量与ui(i∈ Im)正交,所以;最后,如果不满足停止条件(即新余量极微小)或者(即原子下标过多),则循环执行单次迭代。否则,迭代结束。设共迭代了M次,此时有
从上述迭代过程可以看出,StOMP算法是在冗余字典中寻找一个较优的正交基进行分解,但是StOMP算法每次匹配追踪时选出的是多个匹配原子而不是单个原子,不是信号的最佳表示,降低了稀疏分解的精度,提高了计算速度,相当于将OMP算法进行一定程度的简化。
另外,StOMP算法中引入的极限因子一般是预设定的数值,相当于迭代阈值,它对稀疏分解的精度相当敏感,如果设定不当,不仅分解速度受到极大影响,同时稀疏分解和重构精度均大幅降低,甚至完全无法重构。为了克服这个问题,优化StOMP算法性能,经过实验提出了基于余量向量和基向量gr的互相关向量的自适应极限因子选取方法和迭代结束条件重设,取得良好效果。
3 实验与结果
在MATLAB R2014a(8.3.0.532)下编写StOMP及其优化算法程序,冗余字典(即感知矩阵Φ)使用伯努利矩阵,实验信号f为长度N=256的一维信号,该信号中的随机位置上有K (K<N)个服从标准正态分布的非零实数,其余全部为0。依次设定K取值为10、20、30、40、50、60、70、80、90、100时,对照StOMP及其优化算法在迭代次数、选出原子数目、计算速度和重构精度(相对误差)上的差异,实验结果如图1所示。
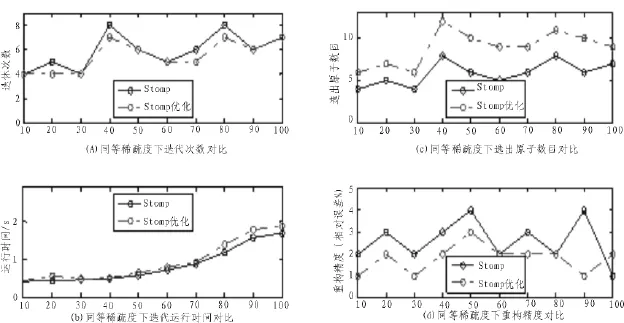
图1 不同稀疏度下StOMP及其优化对比
从实验结果可以看出StOMP优化算法较StOMP算法,在运行时间略微提高的情况下,迭代次数进一步减少,重构精度有较好提升;另外,由于采用基于互相关向量的极限因子,算法的鲁棒性也得到提高。
4 结束语
分段正交匹配追踪StOMP算法因选出的是多个匹配原子而不是单个原子,减少了迭代次数,相当于OMP算法进行了一定程度的简化。StOMP算法进一步优化后,通过实验,在运行时间开销基本增长不大的情况下,增加了算法鲁棒性,重构精度得到提高。未来,可考虑构造自适应冗余字典,进一步提高算法性能。
[1]程涛,朱国宾,刘玉安.压缩感知中高斯矩阵的优化研究[J].计算机应用研究,2014,31(12):3599-3602.
[2]Candès E J,Wakin M B.An Introduction to Compressive Sampling[J].IEEE Signal Processing Magazine,2008,25(2):21-30.
[3]DONOHO D.Compressed sensing[J].IEEE Transactions on In formation Theory,2006,52(4):1289-1306.
[4]方红,杨海蓉.贪婪算法与压缩感知理论[J].自动化学报,2011,37(12):1413-1421.
[5]戴琼海,付长军,季向阳.压缩感知研究[J].计算机学报,2011, 34(3):3425-3434.
[6]王燕霞,张弓.一种改进的用于稀疏表示的正交匹配追踪算法[J].信息与电子工程,2012,10(5):579-583.
[7]姚远,梁志毅.基于压缩感知信号重建的自适应空间正交匹配追踪算法[J].计算机科学,2012,39(10):50-53.
Optimization of segmented orthogonal matching pursuit StOMP algorithm based on compressed sensing
HUANG Tong1,LI Di-na1,SHAO Si-fei1,2
(1.Innovation College of Yan'an University,Xi'an 710100,China;2.College of Physics and Electronic Information Yan'an University,Yan'an 716000,China)
In order to further reduce the number of iterations of segmented orthogonal matching pursuit(StOMP)algorithm and improve the reconstruction accuracy,propose optimization methods of adaptive limit factor selection based on cross-correlation vector and iteration ending condition reset through the analysis of multi atom matching method in the iterative process of StOMP algorithm.MATLAB programming experiment in random test data with given sparse degree k,show that the optimized algorithm reduce iterations 1-2 times,improve reconstruction accuracy by about 1%,increase the robustness than the original StOMP algorithm,while time consumption is almost the same.
compressed sensing;orthogonal matching pursuit algorithm;segmented orthogonal matching pursuit algorithm;StOMP
TN911.72
A
1674-6236(2016)13-0018-03
2015-07-03稿件编号:201507033
陕西省教育厅科研计划项(14JK2170)
黄 同(1980—),男,河南桐柏人,硕士研究生,讲师。研究方向:现代信号处理、系统软件开发和嵌入式系统设计。
