一种改进的稀疏表示DOA估计算法

赵宏伟，刘 波，刘 恒

（西安空间无线电技术研究所 陕西 西安　710100）

一种改进的稀疏表示DOA估计算法

赵宏伟，刘 波，刘 恒

（西安空间无线电技术研究所 陕西 西安710100）

稀疏表示波达方向（DOA）估计算法具有分辨力高等优点，但是对阵元个数要求高、低信噪比时估计性能恶化严重，不利于在实际系统中应用。为此，提出一种基于实信号特点的稀疏表示波达方向估计算法。首先，建立实值稀疏表示的DOA估计模型，能够将阵元数虚拟加倍；其次，利用正交三角分解对估计模型变型，从而改善低信噪比时的估计性能；最后，利用正交匹配追踪算法得到估计结果。仿真实验结果表明，相对传统稀疏表示算法，具有更低的估计误差和更好的实时性，在实际工程中应用前景广阔。

波达方向估计；稀疏表示；正交三角分解；正交匹配追踪

波达方向（Direction of Arrival，DOA）估计技术是阵列信号处理领域的研究重点之一，能够实现空间中多个目标信号的高分辨定位，在雷达、通信、导航等领域有着广泛的应用［1-2］。经典的MUSIC、ESPRIT等算法在高信噪比、足够大的快拍数条件下，才可以很好的实现非相干目标信号方向估计［3］。近年，稀疏表示（Sparse Representation，SR）思想在图像处理、无线通信以及生物医学等领域吸引了研究者们的极大关注［4-6］。基于稀疏表示的DOA估计算法受到学者们的重视。文献［7］提出根据阵列流型建立过完备字典，再利用二阶锥规划法对阵列接收数据进行稀疏分解得到目标DOA信息。文献［8］提出目标角度与过完备字典模型失配时的稀疏表示求解方法。文献［9-12］针对稀疏表示DOA估计算法在不同阵列中的应用进行了研究和优化。这些文献说明，基于稀疏表示的DOA估计算法具有较高的估计性能，天线阵元分布形式、接收信号的相干性不影响算法性能，对快拍数的要求比较低。

基于稀疏表示的DOA估计算法对阵元个数要求比较高、在低信噪比情况下出现性能恶化，并且实时性较差，成为制约应用于实际系统的关键因素。鉴于此，本文利用常用系统中的调制信号为实信号的特点，构建实值的阵列接收数据和过完备字典，然后利用QR分解对数据模型变型，最后采用稀疏恢复算法得到DOA估计结果。仿真实验验证算法的可行性和有效性。

1　基于稀疏表示的DOA估计

1.1DOA估计模型

由M个阵元组成直线阵，如图1所示。假设K个窄带信号入射，由于实际感兴趣目标仅占据少量的空间角度分辨单位，因此这些目标可以构成一个稀疏向量。假设T次快拍下，M×T维的接收数据矩阵为Y；A为M×N维的过完备字典；S 为N×T维的数据矢量，其中仅有K行元素非零，其余元素为0（或极小值，代表噪声）；E为M×T维的复高斯白噪声。相应的DOA估计模型为

式中，||*||0表示L0范数，||*||2表示L2范数，ε为正则化参数，与噪声有关。

1.2算法步骤

基于稀疏表示的DOA估计主要思想是根据阵列流型建立过完备字典，包含所有可能的目标方位信息；再对阵列接收数据进行稀疏恢复，根据重构结果确定目标信号方向。基本步骤为：

1）设置方向间隔，在所有入射方向范围内进行采样，得到方位角采样序列θ=［θ1，θ2，…，θN］，建立对应的过完备字典A=［a（θ1），a（θ2），…，a（θN）］，其中N为信号导向矢量a（θi）的个数；

2）获得阵列接收数据Y；

3）建立稀疏模型（1）；

4）利用稀疏恢复算法求解信号向量S，根据S中非零元素位置得到相应的入射信号方向。

图1　均匀直线阵列接收信号示意图

2　改进的稀疏表示DOA估计

2.1实值估计模型

阵列接收实数信号时，拼接接收信号Y的实部Yc和虚部Ys，重新构造实值阵列接收数据模型为

式中，接收数据Yr为2M×T维；Ec和Es为噪声矩阵E的实部和虚部，构成Er；Ar由阵列流型A的实部Ac与虚部As组成，Ac=［ac（θ1），ac（θ2），…，ac（θN）］，As=［as（θ1），as（s2），…，as（θN）］，对于均匀线阵ac（θi）和as（θi）为式（3）和（4），d为阵元间距。可以证明，Ar依然与噪声子空间相互正交［13］。

相应的DOA估计模型为

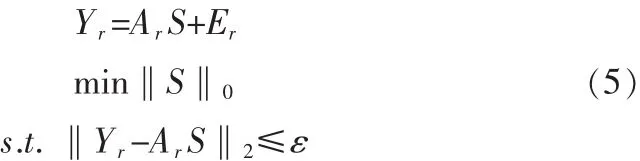
算法在实数基础上进行，简化了运算的复杂性；接收数据维数翻倍，相当于加倍了可用的阵元个数。

2.2正交三角分解

现有的基于稀疏表示理论的测向方法在低信噪比时估计性能恶化较严重，本节采用正交三角（QR）分解对接收数据进行去除噪声预处理，并且降低阵列接收数据维数。对接收数据Yr的伪逆Y+r进行QR分解可得

式中，Q为正交矩阵，QQH=I，I为单位矩阵；R为三角矩阵。

进一步可得

将（6）代入（2）变换得

QR分解相当于对数据进行去噪处理，能够有效降低噪声影响；在大快拍数（如快拍数＞＞阵元数）情况下，将Yr的维数2M×T降为R+的2M×2M。

2.3算法步骤

将本文改进的稀疏表示DOA估计算法步骤总结如下：

1）设置方向间隔，在所有入射方向范围内进行采样，得到方位角采样序列θ=［θ1，θ2，…，θN］，建立对应的实值过完备字典Ar=［ar（θ1），ar（θ2），…，ar（θN）］，ar（θi）=［ac（θi）T，as（θi）T］T；

2）阵列接收数据Y的实部和虚部构建实值阵列接收数据Yr；

3）对Yr进行QR分解获得接收数据子阵R+；

4）建立改进的DOA估计模型为

5）目前稀疏恢复算法主要包括两大类，凸松弛法和贪婪追踪法。前者具有理论保障，但是计算复杂度高，难以用于实际工程中。贪婪类算法的正交匹配追踪算法是一种典型的贪婪追踪算法，简单快速，具有较强的重构能力。因此，这里利用正交匹配追踪（Orthogonal Matching Pursuit，OMP）算法［14］求解模型（8）。

3　性能仿真

在仿真中假设阵元个数为30；阵元之间的间隔为0.5λ，λ为波长；假设在运动目标定位跟踪场合下，最多只能获得20个快拍数。观测空间中存在5个信号源，信源1和2为相干信源，方位角依次为：-5.6°、-1.2°、3.5°和7.8°。

观测空间的细化程度决定了稀疏表示DOA方法估计结果的精度。较大的间隔无法精确区分一个分辨单元内的不同信号，较小的间隔可以提高估计精度，但是相邻原子的相关性增大。通过大量仿真验证，细化间隔为0.1°～1°时，算法一般具有较高的稳健性。这里观测空间为［-10°，10°］，细化间隔设置为0.1°。

仿真中，定义角度估计误差的均方值为

式中，J为独立蒙特卡罗试验次数，设置为500；K为干扰源个数；θk为第k个目标方位真实值；为第j次蒙特卡罗试验对第k个目标的估计值。

实验1实值SR DOA算法验证与分析。

首先，将2.1节的实值Real SR DOA、常规SR DOA（过完备原子库为阵列流型矩阵、采用OMP重构算法）算法［15］以及MUSIC算法进行比较。

各种算法的DOA估计均方根误差随信噪比变化关系曲线的蒙特卡罗实验结果如图2所示。随着信噪比的增大，两种SR算法的估计误差变小。由于快拍数目少且存在相干信号，信号的方向向量与噪声子空间不再满足正交关系，MUSIC算法无法获得精确的角度估计结果。

两种SR算法在信噪比高于0 dB处，误差和成功率都基本稳定，低于0 dB处略有衰减，估计性能优于MUSIC算法。在同等阵元数30等参数一致的情况下，本文实值Real SR算法性能大幅优于常规SR算法（SR 30），与阵元数加倍为60时的常规SR算法（SR 60）性能相当。这是由于新的阵列接收模型（2）虚拟地将阵元个数加倍，提高了算法的估计精度和多个信号的处理能力。

图2　均方根误差随信噪比变化曲线

实验2结合QR分解的实值算法验证与分析。

如图3所示，本文算法（Real SR+QR）采用QR分解进行信号降维及能量累计，具有抑制噪声的作用，估计误差变小，因此改善了传统稀疏表示DOA估计算法的适用范围，提高低信噪比环境下的算法性能，并且明显降低了计算量，减少了运算时间，最多节省15%的时间，如表1所示。（运行环境：台式机；Windows XP SP3；Intel Core2 Quad CPU；2GB内存；Matlab版本为R2008a；仿真次数为500次。）

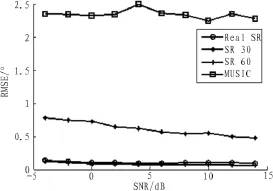
图3　均方根误差随信噪比变化曲线

表1　不同采样间隔下算法平均耗时（秒）

4　结　论

稀疏表示DOA估计［16-17］算法具有可直接处理相干信号、估计精度高等优点，但是对阵元个数要求高、低信噪比时估计性能较差。本文提出一种基于实值信号特点的稀疏表示DOA估计算法，仿真实验证明，构造的实值稀疏模型使可用的阵元个数加倍，提高了算法估计精度；QR分解改善低信噪比下的算法性能；算法运行在实数域，减小了算法计算量。

［1］Matthew J，Christopher D，Michael D.Demonstration of an electrically small antenna array for UHF direction-of-arrival estimation［J］.IEEE Transactions on Antennas and Propagation，2013，61（3）：1371-1377．

［2］孙海浪，陶海红，张娟．用于星载赋形天线的基于频域多相干目标测向算法［J］.宇航学报，2010，31（3）：830-837.

［3］张宏谋，闫剑虹，施锦文.均匀圆阵部分阵元失效情况下的DOA估计方法［J］.电子设计工程，2013，21（19）：26-29.

［4］Romberg J.Imaging via compressive sampling［J］.IEEE Signal Processing Magazine，2008，25（2）：14-20．

［5］ParedesJL，ArcwGR，WangZM.Ultra-Wideband compressed sensing：channel estimation［J］.IEEE Journal of Selected Topics in Signal Processing，2007，1（3）：383-395.

［6］吴凌华，张小川.压缩感知的发展与应用［J］.电讯技术，2011，51（1）：120-124.

［7］MalioutovD，GetinM，WillskySA.Asparsesignal reconstruction perspective for source localization with sensor arrays［J］.IEEE Transaction on Signal Processing，2005，53 （8）：3010-3022.

［8］王超宇，朱晓华，李洪涛，等.一种鲁棒的压缩感知高分辨率DOA估计方法［J］.宇航学报，2014，35（5）：590-596.

［9］王园园，刘峥，曹运合.基于压缩感知的米波雷达低空测角算法［J］.系统工程与电子技术，2014，36（4）：667-671.

［10］MarcoR，AlexanderM，YoninaC.Spatialcompressive sensing for MIMO radar［J］.IEEE Transactions on Siganl Processing，2014，62（2）：419-430.

［11］王赞，陈伯孝.利用压缩感知的分布式高频地波雷达DOA估计［J］.西安电子科技大学学报，2014，41（2）：58-64.

［12］YU Yu，PETROPULU A P，POOR H V.MIMO radar using compressive sampling［J］.IEEE Journal of Selected Topics in Signal Processing，2010，4（1）：146-162.

［13］冯大正，郑春弟，周袆.一种利用信号特点的实值MUSIC算法［J］.电波科学学报，2007，22（2）：331-335.

［14］Thakshila W，Pramod K.OMP based joint sparsity pattern recovery under communication constraints［J］.IEEE Transactions on Siganl Processing，2014，62（19）：5059-5072.

［15］黄传禄，晁坤，毛云志.基于压缩感知的空间谱估计［J］.电波科学学报，2014，29（2）：150-157.

［16］王维猛，焦荣华，邹德财，等.TD-SCDMA系统基于MUSIC算法的DOA估计研究［J］.电子科技，2014（4）：1-4.

［17］郭亚萍，陈建春，彭金龙.基于Root-ISM算法的宽带非相干信号DOA估计［J］.电子科技，2015（6）：38-40.

An improved DOA estimation algorithm with sparse representation

ZHAO Hong-wei，LIU Bo，LIU Heng
（Xi'an Institute of Space Radio Technology，Xi'an 710100，China）

Though the direction of arrival（DOA）estimation with sparse representation has high resolution，its computational load is too much and is not suitable for real-time processing in practical system.A DOA estimation algorithm with sparse representation based on the property of real signal sources is proposed to settle the problem.First，the corresponding DOA model is constructed and the numbers of available sensors is doubled based on the array data model of real signals.Then，the orthogonal triangular（QR）decomposition is used to improve the estimation performance at low SNR.Finally，the direction estimation was obtained by orthogonal matching pursuit algorithm.The results of simulation experiments show that the proposed algorithm is suitable for real-time processing and has low estimation error.Therefore，there is much application prospect in practical system engineering.

direction of arrival estimation；sparse representation；orthogonal triangular decomposition；orthogonal matching pursuit

TN911

A

1674－6236（2016）09-0133-03

2015-11-05稿件编号：201511052

国家自然科学基金（61201089）

赵宏伟（1982—），男，山东潍坊人，博士研究生。研究方向：空间谱估计。