基于单程波动方程的曲面波裂步傅里叶叠前深度偏移

李慧杰，陈秀梅

（同济大学 航空航天与力学学院，上海　200092）

基于单程波动方程的曲面波裂步傅里叶叠前深度偏移

李慧杰，陈秀梅

（同济大学 航空航天与力学学院，上海200092）

波动方程叠前深度偏移方法是当前解决复杂地质构造并精确成像的最有效方法，但常规炮集叠前数据深度偏移涉及到巨大的波场外推计算量，计算效率偏低。这里将曲面波技术与裂步傅里叶算子（SSF）相结合，提出曲面波裂步傅里叶偏移方法。该方法通过构建适合波场理论的曲面波合成算子来合成曲面波数据，然后结合适用于炮域的裂步傅里叶波场延拓算子对曲面波波场进行延拓成像，其能够保证地下目标成像质量的同时进一步极大提高成像效率。应用复杂Marmousi模型成功验证了该方法的高效性和准确性。

单程波动方程；曲面波合成算子；裂步傅里叶；叠前深度偏移

波动方程叠前深度偏移基于地震波动力学规律和波场延拓理论，充分利用叠前原始数据，能够真实地反演出地下构造，是解决复杂构造精确成像最有效的手段［1］，然而这种方法由于波场外需要推花费巨大的计算量。如何在保证成像精度的同时又减少计算量提高计算效率，是研究者一直探索的目标，其研究总体来说有两条线路。

其一是对波场数据的处理。1992年Berkhout提出了一种快速有效的面炮技术［2］，该技术将多个单炮合成一个面炮，将多炮记录合成为一个面炮记录。通过这种技术，不需要对每个炮记录单独偏移，在不损失精度的情况下大大减少了用于偏移的叠前数据量，从而也提高了计算效率。之后陈生昌（2002）把面炮合成偏移方法和Mosher等的偏移距平面波偏移方法［3］放在一个统一的理论框架里，提出了一套基于平面波分解的波动方程叠前深度偏移方法［4］。Chen等（2004，2011）［5-6］拓展了面炮技术，提出了曲面波思想，建立了曲面波合成与偏移理论及方法，并将“曲面波源”与地质深度模型结合，提出了面向目标的地表控制照明技术。这样的理论建立使面炮成像更灵活、更具拓展性。

其二是对波场延拓算子的改进。1978年Gazdag提出相位移法（PS）［7］，该方法无倾角限制，无频散，但由于在ω-kx域中延拓，kx与v（x）的关系无法确定，因而不能适应横向变速情况。Stoffa等（1990）提出一种分裂步Fourier方法（SSF）［8］，该方法基于小扰的理论，将速度场分为背景速度和扰动项之和，并交替在ω-kx域和ω-x域中推导出波场延拓公式，实现对横向速度的变化处理，是权衡偏移效率和偏移精度后较为理想的波场延拓方法。

文中首先以曲面波技术为基础，根据速度模型约束构建曲面波合成算子来得到曲面波震源以及曲面波记录，然后基于适用于炮域的单程波波场延拓理论将高效精确的SSF波场延拓算子应用到曲面波域中，并结合相应成像条件实现曲面波SSF偏移成像。这样在不损失传统炮集数据偏移精度的同时，进一步提高了偏移效率。最后通过Marmousi模型验证该方法的准确性和高效性。

1　曲面波数据的合成

曲面波技术［6］是拓展的面炮技术，其将面炮合成算子作为基核，并赋予基核算子方向照明扰动特性，构建曲面波合成算子。通过合成算子作用将炮集数据记录合成曲面波记录，再适用于单程波动方程偏移算法进行偏移。根据波动原理，曲面波技术同样要求满足面炮偏移的基本物理假设，即曲面波场满足基于地震波场的“WRW”正演离散矩阵模型，且假定地震数据已经消除了与地表地层有关的效应。

1.1面炮合成

由于地震波传播理论是一个线性时不变系统，可对每个频率的成分进行单独处理，故在频率域中考虑波场的传播过程。对于点源记录，根据“WRW”模型，频率域中地表处的单炮点源记录可以表示为其中W-（z0，zn）和W+（zn，z0）分别为上下行波传播算子；x表示地表空间位置；ω表示角频率；R（zn）是反射系数矩阵；S （x，z0；ω）为震源子波。若将地表z0处不同位置激发的点源子波组成矩阵，记为S（z0），相应的观测炮记录组成的矩阵记为P（z0），同时令则式（1）可以转化为以下形式此时定义地表一复数值合成算子向量L（z0）=（L1，L2，L，Ln）T，将它作用于震源波场，得Ssyn（z0）为面炮震源。对方程（3）两边乘以向量L（z0）得

令其中 Psyn（z0）为合成面炮记录。由此可知面炮震源和面炮记录是由震源子波和接收炮记录经过合成算子L（z0）作用后得到的。

1.2曲面波合成算子定义与曲面波合成

由面炮的合成过程可知，合成算子L（z0）为任意复向量，这种合成波场任意性大，复杂情形高。根据Chen （2004，2011）定义，这里给出在地表z0处曲面波合成算子向量的一般表达形式。式中fi=f（xi，z0）是任意二元复数函数，表示在地面炮点xi处的离散样点值，可看作炮点震源子波的相位延迟时间，为任意实函数，表示相位延迟时相对横向变量的x变化率，称为曲面波射线扰动参数。

从定义可知曲面波合成算子仍是任意复向量，且曲面波震源的激发面是一个具有空间横向变化曲率的曲面 （二维为曲线）。当时，算子

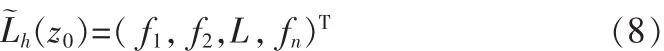
图1　曲面波激发与震源延迟时距关系图

1.3曲面波裂步傅里叶法偏移

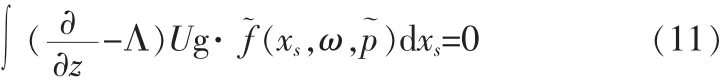
由于算子Λ与xs无关，所以式（12）可以进一步化简为

根据曲面波合成原理

同理可以得到曲面波震源波场函数方程，并结合相应边界条件得到基于单程波动方程的曲面波叠前深度偏移方程

根据摄动理论，将某一空间位置上实际声波速度分解为该深度层上的参考速度v0（z），以及相对参考速度的摄动速度Δv（x，z），这样

裂步傅里叶方法（SSF）正是基于这一理论，将叠前数据深度外推的实现分为2个步骤：第一步是在频率波数域完成的，即针对背景慢度的相移处理；第二步骤是在频率空间域的时移处理，主要是针对慢度扰动的处理［8］。

以曲面波波场记录函数为例，其在深度方向SSF延拓公式为

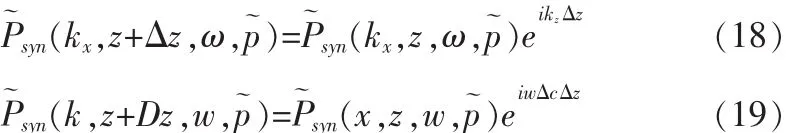
图2显示了曲面波裂步傅里叶法合成与偏移的详细流程。

图2　曲面波SSF偏移流程图

2　模型计算

用公认的Marmousi模型数据验证本文方法，该模型具有相对强烈的横向变速，深层含复杂储集层，是检验叠前深度偏移方法的标准模型，图3为其速度场。模型正演数据共240炮，观测系统为96道接收，炮间距与道间距均为25 m，最小偏移距200 m，最大偏移距2 575 m，记录长度3 s，时间采样率4 ms。

在曲面波数据合成过程中，依据速度模型中的背斜构造约束，给定曲面波基核函数为f（x，z0）=exp（-i10.0ω·x·sin0.00023x），图4显示了基核曲面波震源和相应曲面波记录。图5、6分别是曲面波SSF深度偏移剖面以及传统炮集SSF深度偏移剖面。其中曲面波方法偏移选取取51个曲面波射线扰动参数，其范围为（-350 μs/m，350 μs/m）。从成像结果可以看出，两种方法都能比较清晰地显示浅层的三组大断层和深层的储集体，反映波场随速度变化的趋势，但受SSF算法本身精度影响，也都有明显的噪声背景，尤其在横向速度变化较大区域，细节表现仍然有待提高。

图3　Marmousi速度模型

笔者用PC机对两种计算方法进行计算效率的统计，结果如表1所示。可见曲面波偏移所需时间远远低于常规炮集偏移时间，效率上提高了近5倍，约等于炮数与扰动参数个数之比。

图4　曲面波基核算子及其相应曲面波记录

图5　曲面波裂步傅里叶偏移剖面

图6　传统单程波裂步傅里叶偏移剖面

表1　计算时间对比

3　结　论

基于单程波动方程的裂步傅里叶偏移方法能够兼顾成像效率和精度，其根据速度分裂思想将速度场分为背景速度项和扰动速度项，并交替在域、域实现波场的相移和时移。本文引入了曲面波裂步傅里叶［9-10］偏移方法及具体实现过程，从定义曲面波基核函数出发，并对经过有限个照明方向扫描的合成有限个曲面波记录进行SSF偏移。这样的处理方法极大程度减少了波场外推的计算量，在保证原有延拓算子成像精度的同时进一步提高了成像效率。通过对Marmousi模型偏移结果的对比验证了该方法的高效性准确性和实用性。

［1］刘喜武，刘洪．波动方程地震偏移成像方法的现状与进展［J］．地球物理学进展，2002，17（4）：582－591．

［2］BERKHOUT A J．Areal shot-record technology［J］．Journal of Seismic Exploration，1992，1（2）：251－264．

［3］Mosher C C，Foster D J，Hassassanzadeh S．Common angle imaging with offset plane waves．67th Ann.Internat.Mtg.Soc. Expl.Geophysics，Expanded Abstracts，1997：1379－1382．

［4］陈生昌，曹景忠，马在田，等．平面波偏移法［J］．勘探地球物理进展，2002，25（3）：37－41．

［5］CHEN X M，WANG H Z，Cheng J B，et al．Prestack depth migration by surface rotation controlled illumination［J］．Chinese J Geo-physics，2004，47（1）：306－311．

［6］CHEN X M．MA Z T，WANG H Z，GUO H N．Curved-wave prestack depth migration［J］．Geophysics，2011，76（3）：115－129．

［7］GAZDAG J，SGUAZZERO P．Migration of seismic data by phase shift plus interpolation［J］．Geophysics，1984，49（2）：124－131．

［8］STOFFA P L，et al．Split-step Fourier migration［J］．Geophysics，1990，55（4）：410－421．

［9］尚宇，武小燕.傅里叶级数在心电信号模拟中的应用［J］.西安工业大学学报，2016（1）：21-25.

［10］何金朋，李阳阳，刘罡.基于傅里叶变换的LED单元板均匀性评价方法［J］.电子科技，2013（9）：169-171.

Curved-wave SSF prestack depth migration based on one-way wave equation

LI Hui-jie，CHEN Xiu-mei
（School of Aerospace Engineering and Applied Mechanics，Tongji University，Shanghai 200092，China）

The wave equation prestack depth migration method plays an important role in resolving the problems about seismic imaging of complex geologic bodies in the laterally varying condition.However，conventional wave equation prestack migration based on common shot gathers needs to downward continuation for every trace sample of every shot which involves a huge wave field extrapolation.Here，curved-wave Split-step Fourier prestack migration was put forward by combining curved-wave technology and SSF continuation operator.Curved records and sources were generated by putting curved-wave synthesis operator constructed by defining curved-wave base kernel and a sequence of ray parameters into use，after applying Split-step Fourier continuation operator deduced in shots records to curved records and curved sources，migration imageing result can be achieved in curved-wave field.This kind of processing approach can ensure the quality of imaging of underground targets and further improve the imaging efficiency at the same time.At last，complex Marmousi model was tested to validate the correctness and high efficiency of this method.

one-way wave equation；curved-wave synthesis operator；split-step fourier；prestack migration

TPO

A

1674－6236（2016）09-0072-04

2015-06-03稿件编号：201506045

李慧杰（1988—），男，河北张家口人，硕士研究生。研究方向：地震波偏移技术。