基于极值特征的雷达侦察数据BIRCH聚类方法

张 宇

（中国西南电子技术研究所 四川 成都　610036）

基于极值特征的雷达侦察数据BIRCH聚类方法

张 宇

（中国西南电子技术研究所 四川 成都610036）

为解决传统BIRCH算法对数据对象输入顺序敏感、聚类结果不稳定的问题，提出了一种改进的BIRCH算法。该算法将雷达信号侦察数据的脉冲载频、脉冲重复间隔和脉冲宽度分别进行聚类，根据工程应用中各参数量测误差和系统误差设定不同阈值。并且引入聚类簇的极大极小值作为聚类特征，使用层次树的方法来构建聚类特征模型，实现了雷达侦察数据的快速向下搜索及聚类。实验结果表明，该方法是可行、有效的。

雷达侦察数据；脉冲描述字；BIRCH；极值特征；层次聚类

雷达信号侦察数据处理的参数包含：脉冲前沿到达时间（TOA）、脉冲到达角（DOA）、脉冲载频（RF）、脉冲重复间隔（PRI）、脉冲宽度（PW）、脉冲幅度（PA），统称为脉冲描述字（PDW）。对脉冲载频（RF）、脉冲重复间隔（PRI）和脉冲宽度（PW）分别进行聚类，并在到达时间（TOA）和到达角（DOA）上做进一步时序分析，能够识别雷达辐射源和还原雷达辐射源的工作模式。在雷达信号侦察数据累积数月或数年的前提下，数据量高达TB级，同时雷达信号侦察数据是按时序到达的数据流，不仅需要离线数据聚类，同时也要对实时数据流进行聚类。许多传统的聚类算法［1-2］如平均误差聚类算法［3］、K-均值聚类算法［4］、最近邻算法［5］、PAM算法在时效性和计算资源上已经无法满足需求。传统BIRCH算法［6-8］通过构建聚类特征（Clustering feature）CF树，通过对数据集一次扫描的基础上，增量地对多维数据完成聚类。传统BIRCH算法适用于大规模数据集的聚类，聚类效率高，应用于各个领域。李磊［9］、李晓娴［10］将该方法应用于大规模微博实时抓取数据，通过BIRCH层次聚类的方法得到微博热点列表，结合微博本身特征信息评价微博的热度。王旭［11］首次提出了基于注册信息的学习分组算法，实现了针对学习者学习需求和学习能力等要素的个性化分组。吴春琼［12］则是将BIRCH方法应用于入侵检测。

BIRCH算法在实际聚类中也存在缺陷：对数据对象插入顺序敏感；不善于划分体积差别较大的类别；类别划分会陷入局部最优；节点分裂方式容易将一个中心簇分类为两个对等簇。仰孝富［13］提出基于BIRCH和KNN的改进聚类算法，在构建KNN连接图基础上利用图划分方法得到聚类簇后，再利用BIRCH进行聚类，改善对数据输入顺序的敏感问题，保持聚类的稳定性。周迎春、路嘉伟［14］将CF中数据对象的平方和改进为离差平方和，适应体积差别较大的类别。杨敏煜［15］则是基于密度来划分类别，减少对阈值T的依赖，以及发现任意形状的簇。本文结合工程实际，提出了一种基于极值特征的雷达侦察数据BIRCH聚类方法，该算法将雷达信号侦察数据的脉冲载频、脉冲重复间隔和脉冲宽度分别进行聚类，根据工程应用中各参数量测误差和系统误差设定阈值T。算法选取类别中最大最小值作为类特征，运用阈值T来控制类的数据大小范围，并使用层次树的方法来形成聚类特征模型。仿真结果表明本方法能有效克服BIRCH算法顺序敏感性，提高聚类质量。

1　BIRCH聚类方法

BIRCH算法是一个增量式的层次聚类算法，该算法的主要结构是一棵CF树，聚类的过程都是在这棵树上完成的。而CF树上每个节点又用聚类特征来进行描述。

对于具有N个d维数据点的簇｛xi｝（i=1，2，…，N），它的聚类特征向量定义为：

对于聚类特征有如下定理：

假设CF1=（N1，LS1，SS1）与CF2=（N2，LS2，SS2）分别为两个类的聚类特征，合并后的新类特征为

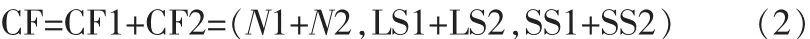
CF树是一棵平衡树，树的宽度由分支节点中最大子节点数决定，每个子节点都有与之相应的一个三元组（聚类特征向量）。各子节点的三元组都被包含在父节点中，每个叶节点也都表示一个簇，为了控制树的规模大小，每个叶节点每个叶节点对应一个阈值T，阈值代表允许的最大直径。也就是簇中任意两节点间距离的均方根。叶节点所代表的簇都不能超过给定的阈值。

在聚类的过程中BIRCH算法自上而下扫描CF树，扫描过程中，所有子节点簇的三元组信息都保存在父节点中。在每个节点逐个被插入到CF树中的过程中，逐渐构造出CF树。为了控制树的规模，如果叶节点超过阈值，则把新节点作为单独的簇来处理。控制树的规模最主要的目的是使其适应主存的规模，为的就是在执行整个聚类过程中数据不用二次读入。具体算法核心骨架如下：

BIRCH算法

输入：阈值T，数据集（x1，…，xn）

输出：类别n for i=1，i从1到n

将xi插入与其最近的一个叶节点中；if插入后的簇小于或等于阈值

将xi插入到该叶节点，并且重新调整从根到此叶节点路径上的所有三元组；elseif插入后节点中有剩余空间

把xi作为一个单独的簇插入并且重新调整从根到此叶节点路径上的所有三元组；else

分裂该节点并调整从根到此叶节点路径上的所有三元组

2　改进的BIRCH聚类方法

本文提出的基于极值特征的雷达侦察数据BIRCH聚类方法，将雷达信号侦察数据的脉冲载频、脉冲重复间隔和脉冲宽度分别进行聚类，根据工程应用中各参数量测误差和系统误差设定阈值T，并且将离线处理后的聚类特征模型用于实时雷达信号侦察数据聚类。

该方法类似于BIRCH算法，聚类的过程也是在一棵CF特征树上完成的，但本方法的CF特征值却不同于BIRCH算法的CF特征值，其表示如下：

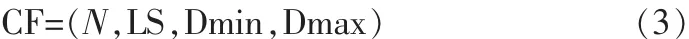
其中N为簇中点的个数；LS表示N个点的线性和；Dmin是簇中数值最小的元素；Dmax是簇中数值最大的元素。

类似于 BIRCH算法，假设：CF1=（N1，LS1，Dmin1，Dmax1）与CF2=（N2，LS2，Dmin2，Dmax2）分别为两个类的聚类特征，合并后的新类特征为：

其中 Dmin=min（Dmin1，Dmin2）；Dmax=max（Dmax1，Dmax2）。

基于极值特征的海量数据层次聚类方法需要在有限的可用内存及计算机资源约束条件下，只需一次扫描数据集就能动态地、递增地对海量雷达数据进行聚类，其中CF树的建立过程如图1所示。

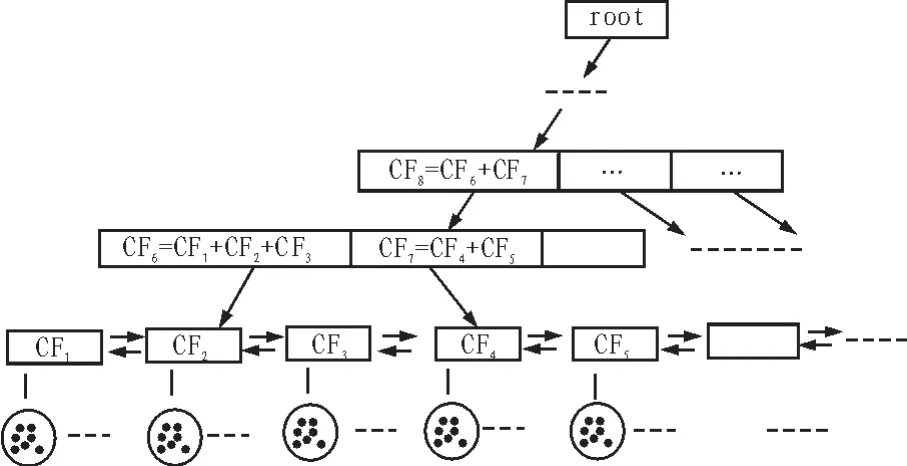
图1　CF树结构示意图

1）找到距离最近的簇：从CF树的根节点向下递归搜索，计算当前节点实体与要插入数据对象之间的距离，具体如下：

设待插入数据为Data，当前节点中实体的CF值为（N，LS，Dmin，Dmax），如果满足

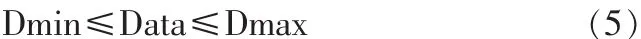
则数据Data沿当前节点继续向下搜索，否则计算Data 与CF的距离

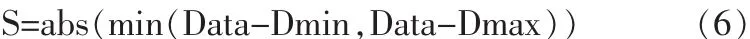
其中abs为取绝对值操作。如果Data与某一节点的所有子节点的CF特征值均不满足式（5）的条件，则运用式（6）分别计算Data与各个子节点之间的距离，然后数据沿着最小距离的子节点继续向下搜索，直到搜索到距离数据Data最近的簇。

2）计算当前簇与数据Data之间的关系，若Data与簇的聚类特征值CF之间满足式（5）的关系，则当前簇直接吸收该数据；若不满足式（5），则计算Data与当前簇中心（也叫簇的质心）之间的距离，簇的中心表示为：

数据与簇中心的距离定义为：

如果距离D小于阈值T，则当前簇吸收该数据为其新元素，并按照式（4）依次向上更新相关节点。若距离D大于阈值T，则需要转到第3步。

阈值T的选择往往需要根据数据的特点或是经验来决定，由于脉冲载频、脉冲重复间隔和脉冲宽度具有不同的精度和置信度，因此在聚类过程中，结合工程应用分别选用不同的阈值进行聚类。

3）判读当前簇所在的叶节点的子女个数是否小于等于L，如果是则直接将该数据Data作为一个新簇插入到当前叶节点下，否则需要分裂该叶节点。设定叶节点所能携带的最大簇的数量为L是为了能够对新数据进行快速的搜索和插入，从而建立起具有层次的CF树。

分裂的原则是寻找该叶节点中距离最远的两个簇，并以这两个簇作为分裂后新的两个叶节点的起始簇，其他剩下的簇根据距离最小原则分配到这两个新的叶节点中，删除原叶节点并更新整棵CF树。节点分裂的示意图如图2所示。

图2　叶节点分裂示意图

在计算机资源及处理时间允许的条件下，可以通过迭代来提升聚类的精确程度。

3　数值分析

为了验证本文方法的有效性，在JAVA环境下进行编程试验并数值分析，采用真实雷达信号侦察数据作为数据源，分别运用传统BIRCH算法和本文方法进行聚类，并对结果进行对比分析。采用SSQ（Sum of Square Distance）来评估聚类的效果，它通过计算所有数据点到各自的聚类中心的距离来衡量算法所给出的聚类的质量。SSQ越小，说明聚类质量越好。SSQ的计算方法如下：

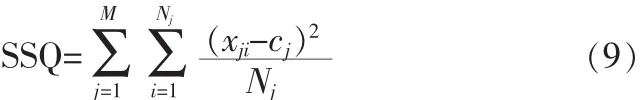
其中，M表示聚类产生的簇数量；Nj表示第j类的数据个数；cj表示第j类的质心；xji表示属于第j类的第i个数据。

通过仿真，得到了BIRCH算法与本文方法的对比结果如图3、图4和表1所示。

从图3与图4可以看出，对雷达数据的脉冲载频进行聚类时，在BIRCH方法中，相同或接近的数据会因为读取的顺序不同而有可能被分为不同的类别，从而导致聚类的错误发生，同样在脉冲重复间隔和脉冲宽度的聚类中也会出现类似情况，而本文提出的基于极值特征的雷达侦察数据BIRCH聚类方法，因采用了簇中最大最小值作为聚类特征，有效避免了该类错误的出现。从表1看出，无论是雷达侦察信号的脉冲载频、脉冲重复间隔还是脉冲宽度，本文方法的聚类SSQ均小于BIRCH算法的聚类SSQ值，这说明本文方法的聚类质量较BIRCH算法更加优良，更能反映数据的真实情况，为后续的数据及情报挖掘提供了真实可靠的理论依据。

图3　BIRCH方法对脉冲载频聚类部分结果

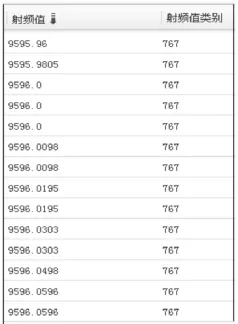
图4　本文方法对脉冲载频聚类部分结果

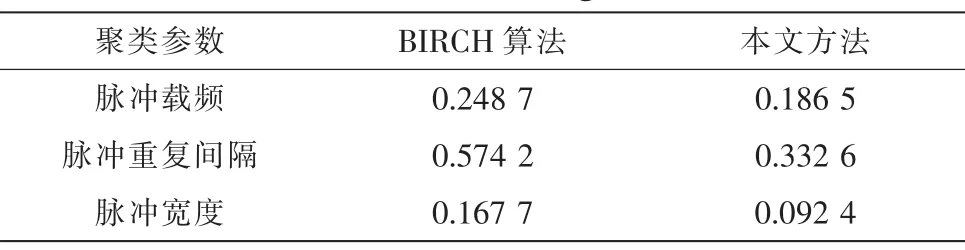
表1　聚类结果SSQ对比

4　结束语

本文提出了基于极值特征的雷达侦察数据BIRCH聚类方法，该方法在传统BIRCH算法基础上，将簇的最大最小值作为独立的聚类特征，并优化了距离度量方法和搜索策略。仿真结果表明，本文方法不但有效改善传统BIRCH算法因为数据读取顺序造成的错分问题，还提高了雷达信号侦察数据的聚类质量，在雷达侦察信号的脉冲载频、脉冲重复间隔还是脉冲宽度聚类上SSQ值均小于传统BIRCH算法。本文方法已在相关工程设计中应用，并在时效性和计算资源上能够较好满足工程需求，具有重要的应用价值。

［1］HAN J，KAMBER M.数据挖掘概念与技术［M］.范明，孟小峰，译.北京：机械工业出版社，2006.

［2］王实，高文.数据挖掘中的聚类方法［J］.计算机科学，2000，27（4）：42-45.

［3］单世民，于红，张业嘉诚，等.基于最近共享邻居节点的K-means聚类算法［J］.计算机工程与应用，2008，44（6）：178-181.

［4］Krishma K，Murty M N.Genetic k-means algorithm［J］.-IEEE Transon System：Man，and Cybernetics，Part B，1999，9（3）：433-439.

［5］JARVISR A，PATRICK E A.Clustering using a similarity measure based on shared nearest neighbors［J］.IEEE Trans on Computers：1973，22（11）：1025-1034.

［6］Zhang T，Ramakrishnan R，Livny M.BIRCH：An efficient data clustering method for very large databases［C］//In：Proc. ACM SIGMOD Conf.Management of Data.Montreal，1996：103-114.

［7］张蓉，钟艳.基于BIRCH算法的模糊集数据库挖掘算法［J］.科技通报，2014，30（4）：47-49.

［8］丁光华.基于BIRCH和GAD的谱聚类算法研究［D］.广州：暨南大学，2010.

［9］李磊.基于新浪微博的热点话题发现系统研究与实现［D］.上海：复旦大学，2013.

［10］李晓娴.微博热点话题发现的研究［D］.北京：北京交通大学，2014.

［11］王旭.汉语学习平台中基于BIRCH聚类的用户个人信息分组算法研究［D］.长春：吉林大学，2011.

［12］吴春琼.基于聚类型BIRCH算法进行数据挖掘的入侵检测模型设计与实现［J］.科技通报，2013，29（8）：136-138.

［13］仰孝富.基于BIRCH改进算法的文本聚类研究［D］.北京：北京林业大学，2013.

［14］周迎春，路嘉伟.一种改进的BIRCH聚类分析算法及其应用研究［J］.湛江师范学院学报，2009，30（3）：83-87.

［15］杨敏煜.基于改进聚类算法的数据挖掘系统的研究与实现［D］.成都：电子科技大学，2012.

An improved BIRCH clustering method for radar reconnaissance data based on extremum features

ZHANG Yu
（Southwest China Institute of Electronic Technology，Chengdu 610036，China）

In order to solve the problem that traditional BIRCH clustering algorithms are sensitive to the data input order with unstable clustering results，an improved BIRCH clustering algorithm is proposed.In this method，the RF，PRI and PW values of radar reconnaissance data are clustered as three separate parameters.In engineering application，different threshold is set according to the parameter measurement error and system error.The maximum and minimum of clusters are used as clustering features to construct the clustering feature model by using hierarchical tree method.The searching and clustering for radar reconnaissance data can be quickly achieved.Experimental results show that the proposed method is feasible and effective.

radar reconnaissance data；PDW；BIRCH；extremum features；hierarchical clustering

TN95

A

1674－6236（2016）09-0015-04

2015-12-28稿件编号：201512288

973国家安全重大基础研究项目（613181）

张 宇（1981—），男，河北魏县人，硕士，工程师。研究方向：数据挖掘与数据处理。