基于改进模糊C均值聚类和MPSO的风电场等值研究

杜晓岩，尹华杰，叶超，杨苹

(华南理工大学 电力学院，广东 广州 510640)



基于改进模糊C均值聚类和MPSO的风电场等值研究

杜晓岩，尹华杰，叶超，杨苹

(华南理工大学 电力学院，广东 广州 510640)

为了提高双馈风电场等值模型的精准度，提出了一种双馈风电场等值建模方法。首先选取能表征各个机组运行状态的特征状态变量矩阵作为分群指标，采用改进模糊C均值聚类算法进行机群划分；然后基于全局最优位置变异粒子群算法对等值机模型的参数进行辨识，将同群的机组等值成一台风机。利用DIgSILENT/PowerFactory平台进行仿真建模，对风电场发生风速阶跃变化和三相短路故障2种状态进行仿真，仿真结果表明，该等值模型与详细模型的动态特性基本一致，比传统的单机等值模型更适合表征双馈风电场的工况。

双馈风力发电机；分群；聚类算法；粒子群；参数识别

在被利用的可再生能源中，风能占据了明显的优势，随着风力发电技术的日益成熟，风电场的并网规模也越来越大。与常规能源相比，风力发电出力具有强波动性的特点，大规模风电并网对电力系统的安全稳定运行有着重要的影响[1]。因此，研究大规模风电场接入后的电网运行特性具有重要的现实意义，而风电场的等值建模是其中需解决的重要问题。

目前常用的风电场动态等值建模方法主要有2种：一种是单机等值法；另一种是多机等值法，先将风电场进行聚类分群，每群组风机再等值成一台风机[2-4]。大型风电场受机群分布不规则、所处地形复杂、存在尾流效应等因素影响，使各风电机组的运行工况不同[5-7]。当风电机组运行状态相差较大时，单机等值法无法表征等值前风电机组的实际运行状态[8]。文献[9]详细考虑了风力机的运行状态，将13个运行状态作为机群分类指标，但计算相当复杂，不适合工程应用。工程上一般采用加权求和法来进行等值机参数聚合[5]，但该方法需已知详细的风电机组参数，在数据不全或未知的场合则需采用优化算法，根据风电场并网点公共连接点(pointofcommoncoupling，PCC)的有功功率、无功功率和电压等测量数据来搜索等值模型参数。

针对当前等值建模存在的问题，本文提出一种双馈风电场动态等值建模方法。首先选取能表征各个机组运行状态的特征状态变量矩阵作为分群指标，采用改进模糊C均值聚类算法进行机群划分；然后基于全局最优位置变异粒子群(globaloptimummutationparticleswarmoptimization，MPSO)算法[10]对等值机模型的参数进行辨识，将同群的机组等值成一台风机；最后利用DIgSILENT/PowerFactory平台建立仿真模型，对风电场发生风速阶跃变化和三相短路故障2种状态进行仿真，结果表明建立的风电场动态等值模型与详细模型误差较小，能够准确地反映风电场动态运行工况。

1　风电场分群指标

在等值过程中，参考大型电力系统暂态稳定分析常采用的同调等值法的思想，使用描述双馈风电机组运行工况的状态变量作为分群指标，将具有相同或者相似工况的双馈风电机组划分成一群，每个机群等值成一台风机。

在两相旋转坐标系下，双馈风力发电机的稳态电压方程为：

(1)

式中：Rs为定子电阻，Rr为转子电阻，s为转差率，Uds、Uqs分别为定子电压的d、q轴分量，Ids、Iqs分别为定子绕组电流的d、q轴分量，Udr、Uqr分别为转子外加电压的d、q轴分量，Idr、Iqr分别为转子绕组电流的d、q轴分量，ψds、ψqs分别为定子磁链的d、q轴分量，ψdr、ψqr分别为转子磁链的d、q轴分量。

磁链方程为：

(2)

式中：Xs为定子回路电抗，Xr为转子回路电抗，Xm为激磁电抗。

有功功率和无功功率有如下关系：

(3)

式中：Ps、Qs分别为定子侧有功功率、无功功率，Pr、Qr分别为转子侧有功功率、无功功率。

电磁转矩

采用定子磁场定向矢量控制，即两相同步旋转坐标系的d轴与定子旋转磁场重合时，忽略定子电阻Rs，可得：

(4)

式中：ψs为定子磁链，Us为定子电压。

将式(4)代入式(3)，得：

(5)

由式(5)可知，通过调节Iqs就可控制发电机的电磁转矩，从而改变发电机的转速。采用定子磁场矢量定向控制方法，通过控制Iqs、Ids分别控制定子侧的有功功率、无功功率，实现发电机功率的解耦控制。

将式(2)代入定子磁链方程，可得：

(6)

将式(6)代入式(1)和式(2)，可得：

(7)

由式(6)和式(7)可知：通过调节转子电压就可控制定子电流，从而控制发电机定子侧的有功功率和无功功率。

双馈风力发电机的定子直接与电网相连，转子经过双脉冲宽度调制(pulsewidthmodulation，PWM)变流器与电网相连，双PWM变流器的功率因数在通常情况下控制为1。因为转子侧有功功率很小且无功功率接近于零，所以双馈风力发电机发出的无功功率可以认为等于定子侧的无功功率。即：

(8)

式中Pe、Qe分别为双馈风力发电机输出的有功功率、无功功率。

双馈风电机组常采用恒功率因数控制方式，即

式中：φ为功角，A为常数。

联立式(6)—(8)，可得到双馈风力发电机的功率关系表达式：

由式(1)—(7)可知：若已知双馈风电机组的风速v、转差率s、双馈风力发电机输出的有功功率Pe、功率因数cosφ、定子端电压Us，即可得双馈发电机定子和转子的有功功率、无功功率，以及定子的电压和电流等状态变量，所以可将[v，s，Pe，cosφ，Us]作为双馈风电机组的特征状态变量。因为采用恒功率因数控制，即cosφ=1，且Us在风电场中相差较小，转差率s与转速ω等价，所以本文选择[v，ω，Pe]作为双馈风电机组的分群指标。

2　基于改进模糊C均值聚类算法的机群划分

在双馈风电机组分群中，采用常用的聚类方法(如K-Means聚类算法)对类与类间有交叉的数据进行分类时，产生的聚类结果不稳定，对等值建模结果精度有影响。改进模糊C均值聚类算法能够有效地改善类间交叉数据集的聚类结果，提高双馈风电场的等值建模精度。

2.1步骤1

选取双馈风电场某长时间段内各机组的特征状态变量矩阵[v，ω，Pe]作为样本，将n台机组的特征状态变量按行建立样本矩阵，得：

式中：S为机组样本矩阵，vi、ωi、Pi分别为第i台双馈风电机组的风速、转速、输出功率。

2.2步骤2

在考虑双馈风电场的实际规模和满足等值模型精度要求的基础上，选取聚类的数目C，将所有双馈风电机组分成C类。

2.3步骤3

改进模糊C均值聚类算法在标准模糊C均值聚类算法的基础上，充分考虑样本特征对分类结果的不同贡献，在目标函数中加了个权值q，其最终目标是使各个分类中的样本点到聚类中心的加权距离平方和达到最小。定义聚类目标函数

(9)

式中：μj为样本i对第j个分类的隶属度，xi为第i个样本，mj为第j个聚类中心，b为大于1的常数，qi为样本i的权值。

全部样本对于各个分类的隶属度总和为

(10)

根据式(10)，利用式(9)分别对mj和μj求解偏导数，得：

(11)

(12)

2.4步骤4

重复以下运算：用当前的μj(xi)结合式(11)更新各个分类的聚类中心，并用新的聚类中心按照式(12)重新计算新的μj(xi)，重复以上运算，直至各个样本的μj(xi)值趋于稳定。

2.5步骤5

计算数据样本i的轮廓值S(i)，判断S(i)是否满足条件。轮廓值S(i)定义为：

式中：a为样本i与同簇内剩余样本之间的平均距离度量；d为一个向量，其元素是样本i与不同簇样本之间的平均距离度量。S(i)的取值范围为[-1，1]，S(i)的值越接近1，说明样本的分类越合理，当S(i)<0时，说明样本的分类不合理。

当μj(xi)收敛时，就可以得到各个分类的聚类中心和各样本对每一类的隶属度，从而完成基于改进模糊C均值聚类算法的双馈风电场机群的划分，把全部的风电机组按照特征状态矢量划分为C类。

3　基于MPSO算法的风力发电机组参数辨识

在粒子群算法中，用每个粒子所处的位置代表待优化问题的解，粒子的性能由目标函数求出的适应度确定，每个粒子由一个速度矢量决定其飞行的方向和大小。MPSO算法是当全局最优位置处的适应值在经过连续多次未得到优化时，对原有粒子群的全局最优位置进行变异，从而使粒子群能够获得新的搜索位置，有效避免了整个粒子陷入局部最优的缺陷。

3.1流程图

MPSO算法的流程如图1所示。

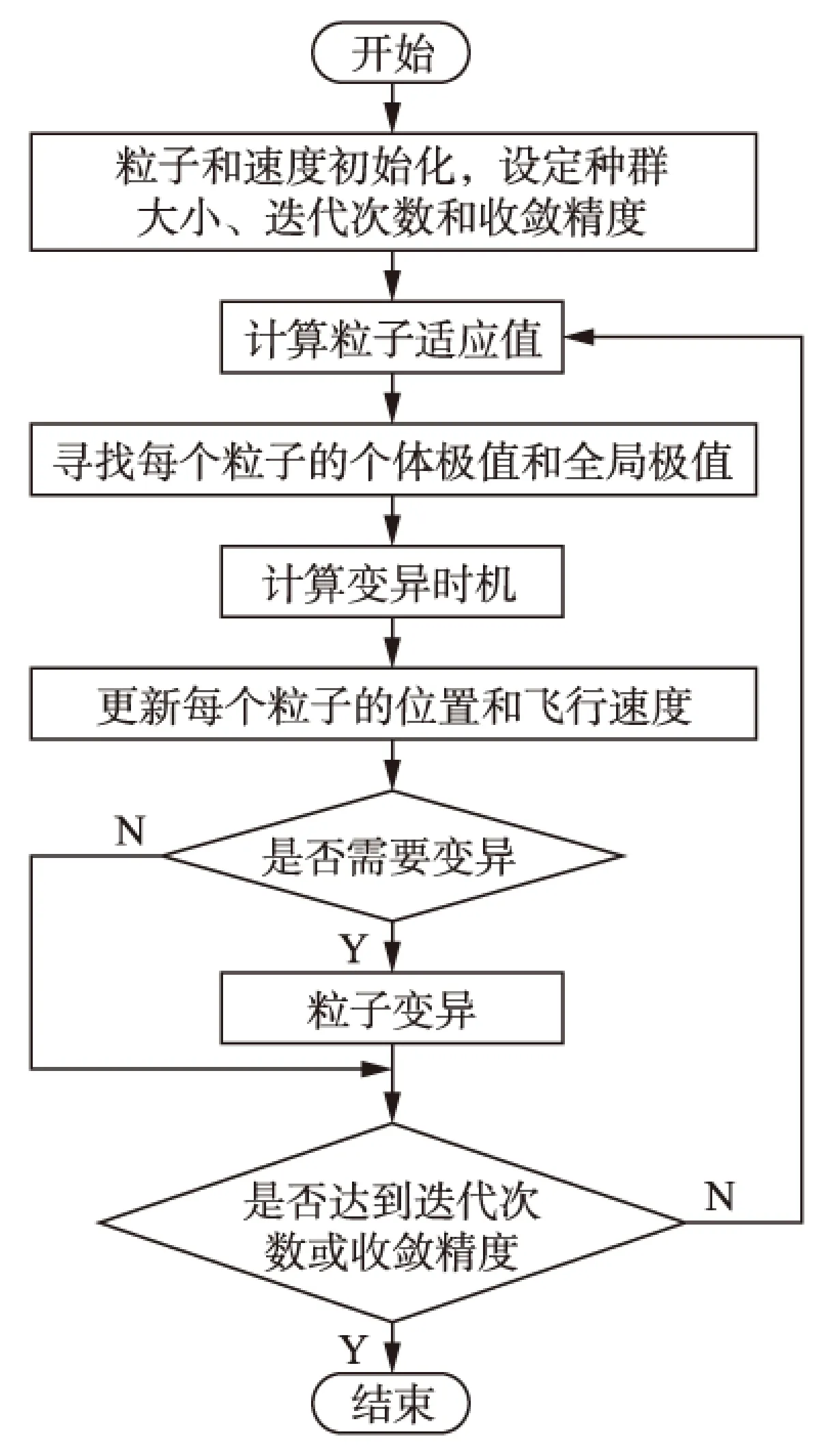
图1　MPSO算法流程

3.2实施步骤

3.2.1步骤1

基于MPSO算法以等值前后风电场有功功率偏差的平方和最小为优化目标函数，在整个解空间上寻优，根据概率意义确定满足优化目标函数的等值机模型的参数。定义目标函数

式中：M为等值前后有功功率的采样点数，Poi为样本的有功功率曲线上第i个采样点的有功功率值，Pi为等值后第i个点的有功功率输出值。

3.2.2步骤2

选择待辨识参数，为定子电阻Rs、转子电阻Rr、定子电感Ls、转子电感Lr、励磁电感Lm，初始化粒子群体的位置、速度、种群大小以及粒子位置和速度的上下限，设置迭代次数、收敛精度、相关权系数和搜索区间。首先利用容量加权平均法计算单一等值风力发电机的参数，然后将该参考值分别乘以2和0.5作为粒子群搜索范围的上、下限，这样能有效地避免搜索区间过大导致参数辨识时间增加和辨识精度降低的问题，也避免了搜索区间太小而忽略最优值的问题。在容量加权法中，等值风力发电机各参数的计算方法为：

式中：ZrA为等值转子阻抗，ZsA为等值定子阻抗，ZmA为等值励磁阻抗，Zsi为第i个风力发电机组的定子阻抗，Zri为第i个风力发电机组的转子阻抗，Zmi为第i个风力发电机组的励磁阻抗，wi为第i个风力发电机组的加权系数，n为风电机组台数。3.2.3步骤3

计算粒子的适应值，将每个粒子的适应值与个体极值、全局极值作比较，取其中的最优值，并更新个体极值和全局极值。

3.2.4步骤4

不停地更新每个粒子的位置和速度，第t+1次迭代计算时，粒子i的更新规则为

其中

式中：w为惯性权重系数，c1、c2为学习因子，rand1(0,1)和 rand2(0,1)为2个均匀分布在(0,1)之间的随机数，m为粒子的个数，vi为第i个粒子的速度；xi为第i个粒子的位置；pp为个体极值，pg为全局极值。粒子在每一维的更新速度vi都小于或者等于最大速度vmax。

3.2.5步骤5

计算变异时机，并判断是否需要变异。

3.2.6步骤6

重复步骤3至步骤5，通过不断调整解向量，将等值模型输出的功率曲线P与原模型输出的功率曲线P0进行拟合，直至达到迭代次数或收敛精度，确定最优解向量，从而获得等值风电机组各项参数的最优值。

4　算例分析

采用中国某地区总装机容量为49.5 MW的风电场，该风电场由33台容量为1.5 MW的双馈风电机组构成，每 11 台双馈风力发电机为一排。在DIgSILENT/ Power Factory平台上建立其详细模型，风电机组定子端额定电压为690 V，采用“一机一变”的方式升压到10 kV，经由风电场集总变压器(变比为10 kV/110 kV)连接到电网。

作为划群指标的风电机组的特征状态矩阵见表1。

采用改进模糊C均值聚类算法对33台机组进行机群划分，结果见表2。

图2为基于改进模糊C均值聚类算法的轮廓值。由图2可知，每个机组的聚类轮廓值都大于0.5，表明聚类结果是比较合理的。

表2基于改进模糊C均值聚类算法的机群划分结果

等值机编号聚类结果11,2,4,9,10,12,13,15,18,19,20,23,24,26,27,3123,6,11,16,22,30,3235,7,8,14,17,21,25,28,29,33

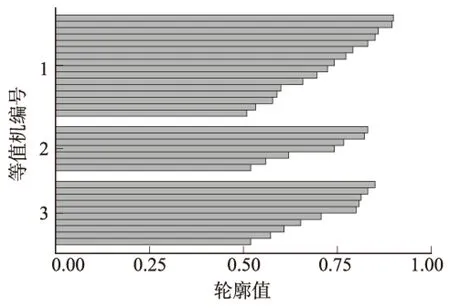
图2　基于改进模糊C均值聚类算法的轮廓值

在机群划分的基础上，以第3组等值机作为风电机群动态等值建模研究对象进行分析。MPSO算法的搜索区域见表3。

表3第3组等值机参数的搜索空间

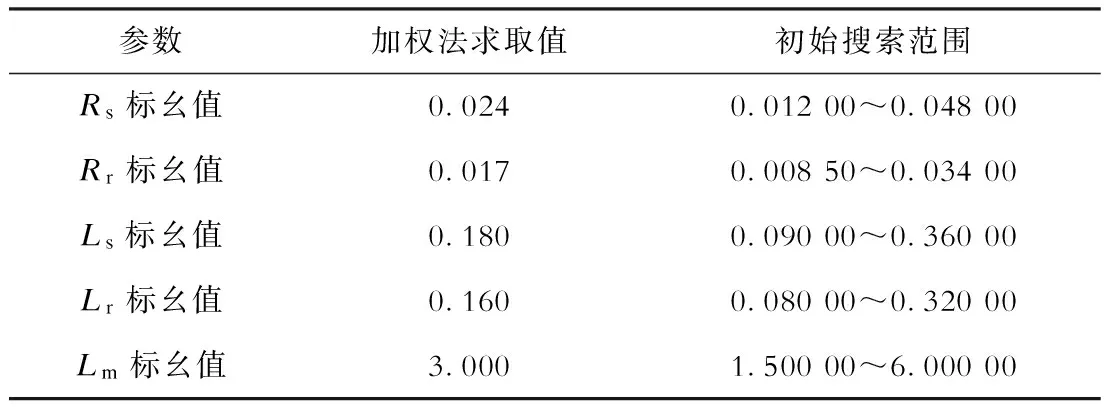
参数加权法求取值初始搜索范围Rs标幺值0.0240.01200～0.04800Rr标幺值0.0170.00850～0.03400Ls标幺值0.1800.09000～0.36000Lr标幺值0.1600.08000～0.32000Lm标幺值3.0001.50000～6.00000

经过在5维空间中的10次迭代，最终收敛到真实值附近的很小范围的寻优值。Rs、Rr、Ls、Lr、Lm的标幺值寻优值分别为0.012 0、0.008 4、0.180 2、0.160 2、2.903 8，等值机参数辨识过程如图3所示。

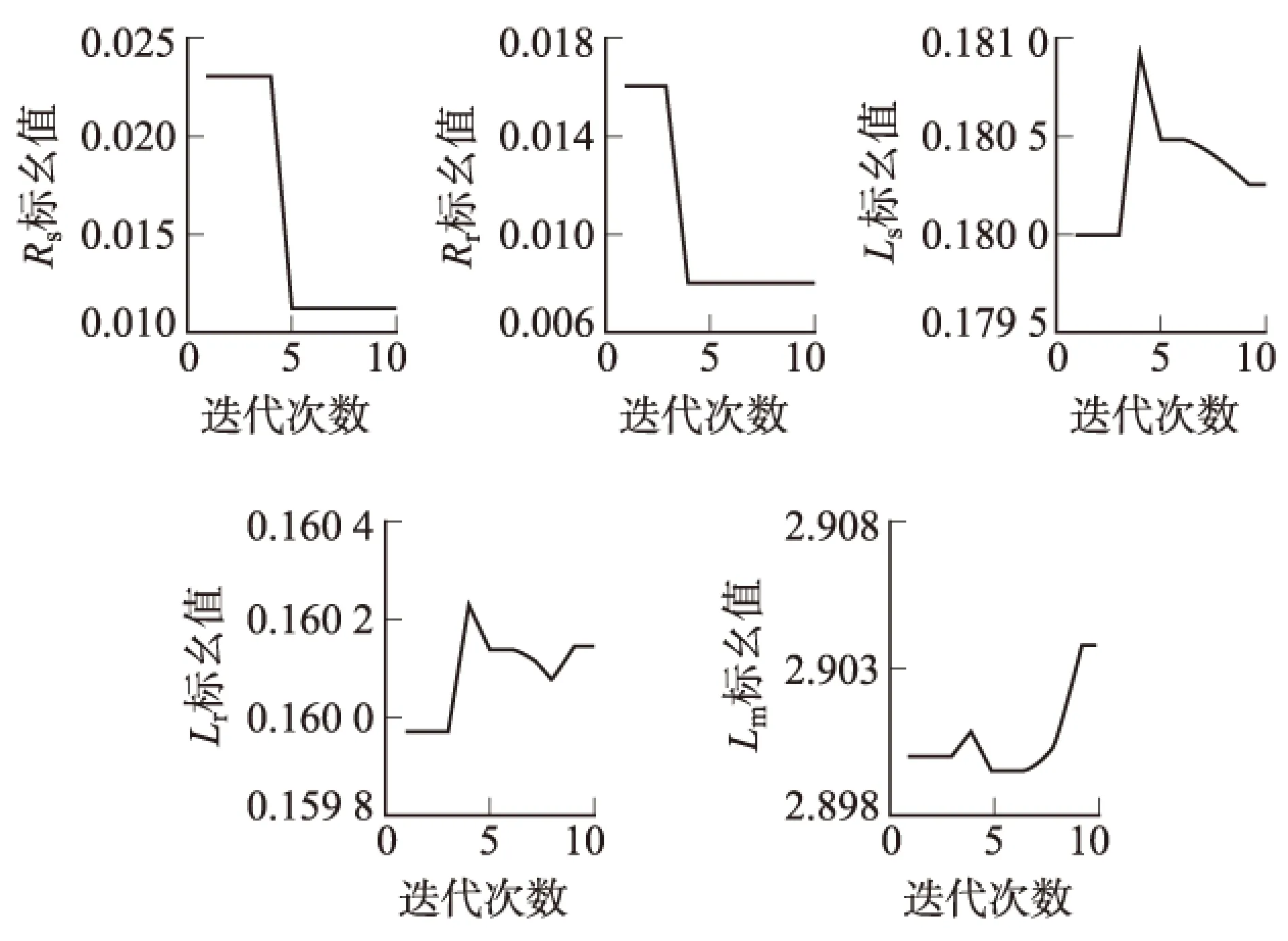
图3　等值机参数辨识结果

经过风电场内机群划分和参数辨识2个步骤后，建立了双馈风电场动态等值模型，仿真结果如图4和图5所示。在图4中，4 s时风速发生阶跃变化。在图5中，2 s时发生三相短路故障，2.4 s时故障清除。

图4　风速发生阶跃变化时的风电场出力曲线

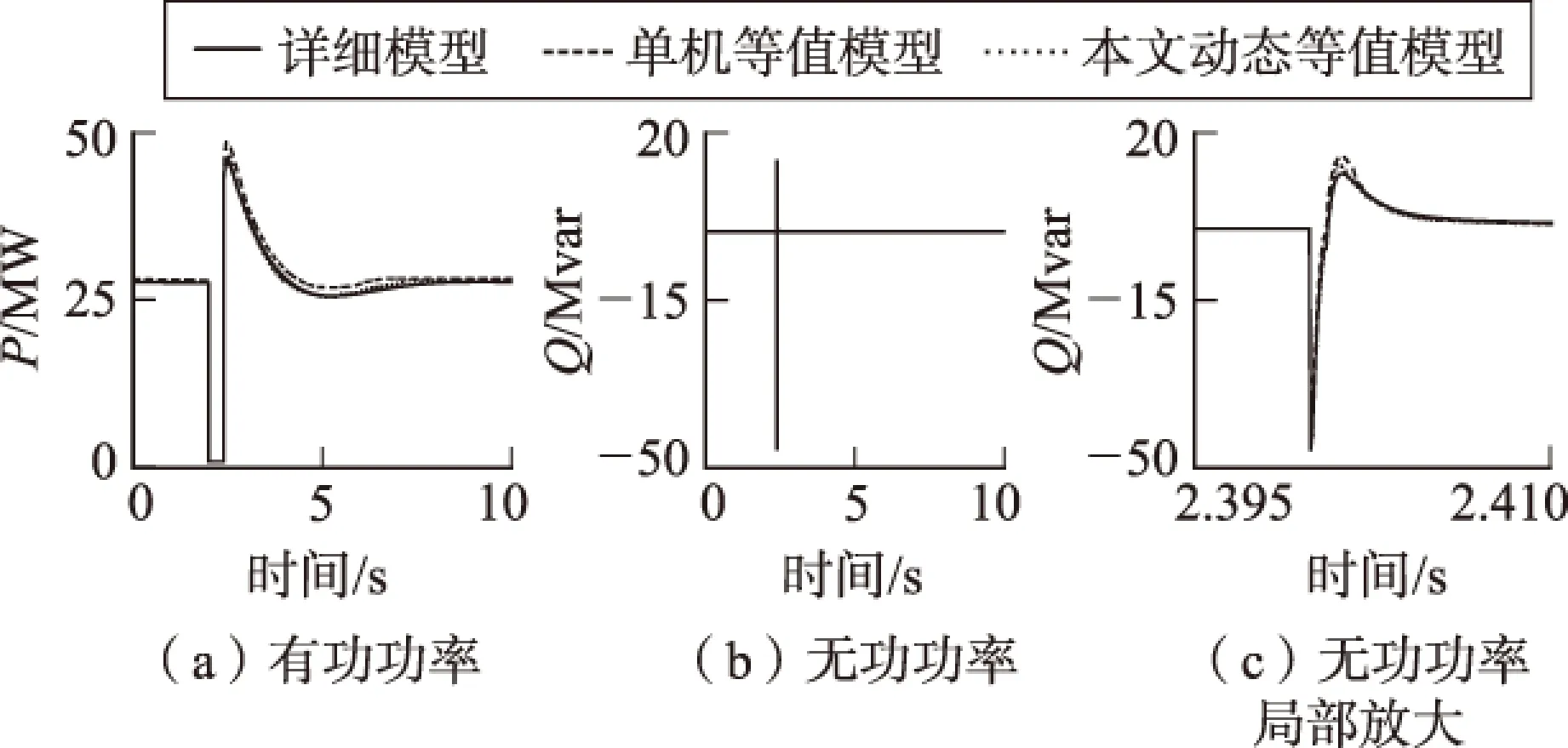
图5　系统侧故障时的风电场出力曲线

由图4和图5可知：当发生风速波动或系统故障时，相比于单机等值方法，本文的风电场动态等值方法的风电场有功功率曲线、无功功率曲线与详细模型几乎一致，具有很高的精度。

5　结论

针对当前双馈等值模型存在的问题，提出了一种双馈风电场动态等值建模方法。首先选取双馈风电场某长时间段内各机组的特征状态变量矩阵[v，ω，Pe]作为分群指标，采用改进模糊C均值聚类算法进行机群划分，然后基于MPSO算法对等值机模型的参数进行辨识，把属于一个机群的双馈风电机组等值成一台风机。利用DIgSILENT/PowerFactory平台进行仿真建模，对风电场发生风速阶跃变化和三相短路故障2种状态进行仿真，结果表明本文建立的风电场动态等值模型与详细模型误差较小，能够较准确地反映风电场动态运行工况。

该方法与单机等值模型相比精度较高，在分析大规模双馈风电场接入对电网的影响时，建立的风电场动态等值模型能够更精准地反映风电场的动态运行特性，可用于含双馈机组风电场接入电力系统的稳定性分析。

[1]余洋，刘永光，董胜元. 基于运行数据的风电场等效建模方法比较[J]. 电网与清洁能源，2009,25(12)：79-83.

YU Yang, LIU Yongguang, DONG Shengyuan. Comparative Study on Wind Farm Equivalent Modeling Based on Operation Data[J]. Power System and Clean Energy,2009,25(12):79-83.

[2]张建设,李浩,黄家栋,等. 双馈式风力发电系统实时数字仿真研究[J]. 南方电网技术,2014,8(6):104-108.

ZHANG Jianshe,LI Hao,HUANG Jiadong,et al. Research on Real-Time Digital Simulation of Doubly-fed Wind Power Generation System[J]. Southern Power System Technology,2014,8(6):104-108.

[3]雷亚洲，GORDON L. 国外风力发电导则及动态模型简介[J]. 电网技术,2005,25(12):27-32.

LEI Yazhou,GORDON L. An Introduction on Wind Power Grid Code and Dynamic Simulation[J]. Power System Technology,2005,25(12):27-32.

[4]陈树勇，戴慧珠，白晓民，等.尾流效应对风电场输出功率的影响[J]. 中国电力，1998，31(11)：28-31.

CHEN Shuyong,DAI Huizhu,BAI Xiaomin,et al. Impact of Wind Turbine Wake on Wind Power Output[J]. Electric Power,1998,31(11):28-31.

[5]曹军,张榕林,林国庆,等.变速恒频双馈电机风电场电压控制策略[J]. 电力系统自动化，2009,33(4):87-91.

CAO Jun,ZHANG Ronglin,LIN Guoqing,et al. A Voltage Control Strategy for Wind Farms Using Doubly Fed Induction Generator Wind Turbines[J]. Automation of Electric Power Systems,2009,33(4):87-91.

[6]郎永强,张学广,徐殿国，等.双馈电机风电场无功功率分析及控制策略[J]. 中国电机工程学报,2007,27(9):77-83.

LANG Yongqiang,ZHANG Xueguang,XU Dianguo,et al. Reactive Power Analysis and Control of Doubly Fed Induction Generator Wind Farm[J]. Proceedings of the CSEE,2007,27(9):77-83.

[7]苏勋文，米增强，王毅. 风电场常用等值方法的适用性及其改进研究[J]. 电网技术,2010,34(6)：175-180.

SU Xunwen, MI Zengqiang, WANG Yi. Applicability and Improvement of Common-Used Equivalent Methods for Wind Farms[J]. Power System Technology,2010, 34(6):175-180.

[8]米增强，苏勋文，杨奇逊，等. 风电场动态等值模型的多机表征方法[J]. 电工技术学报，2010，25(5)：162-169.

MI Zengqiang, SU Xunwen,YANG Qixun, et al. Multi-Machine Representation Method for Dynamic Equivalent Model of Wind Farms[J]. Transactions of China Electrotechnical Society,2010,25(5):162-169.

[9]米增强，苏勋文，余洋，等. 双馈机组风电场动态等效模型研究[J]. 电力系统自动化，2010,34(17)：72-77.

MI Zengqiang, SU Xunwen, YU Yang, et al. Study on Dynamic Equivalence Model of Wind Farms with Wind Turbine Driven Doubly Fed Induction Generator[J]. Automation of Electric Power Systems，2010,34(17):72-77.

[10]范国英，史坤鹏，郑太一，等. 风电场集群接入系统后的聚类分析[J]. 电网技术,2011,35(11)：62-66.

FAN Guoying, SHI Kunpeng, ZHENG Taiyi,et al. Cluster Analysis of Grid-Connected Large Scale Wind Farms[J]. Power System Technology,2011,35(11):62-66.

(编辑李丽娟)

Equivalent Model of Wind Power Farm Based on Improved Fuzzy CMeansClusteringandMPSO

DU Xiaoyan, YIN Huajie, YE Chao, YANG Ping

(SchoolofElectricPower,SouthChinaUniversityofTechnology,Guangzhou,Guangdong510640,China)

Inordertoimproveprecisionoftheequivalencemodelfordoublyfedwindpowerfarm,thispaperproposesakindofequivalentmodelingmethodfordoublyfedwindfarm.Itfirstlyselectscharacteristicstatevariablematrixwhichcanrepresentoperatingstatesofrunningwindgeneratorsastheclusteringindex,andusesimprovedfuzzyCmeansclusteringalgorithmtodividethecluster.Basedonglobaloptimummutationparticleswarmoptimizationalgorithm,parametersoftheequivalentmodelareidentifiedandthesamegroupofgeneratorsareequivalenttobeonewindturbine.Finally,DIgSILENT/PowerFactoryplatformisusedforsimulatingandmodelingfortwokindsofstatesofthewindfarmincludingwindspeedstepchangeandthree-phaseshort-circuitfault.Theresultsindicatethatdynamiccharacteristicofthisequivalentmodelisbasicallyconsistentwiththatofthedetailedmodel.Theequivalentmodelismoresuitableforrepresentingworkingconditionofthedoublyfedwindpowerfarmthantraditionalsinglegeneratorequivalentmodel.

doublyfedwindpowergenerator;clustering;clusteringalgorithm;particleswarm;parameteridentification

2016-03-08

2016-05-10

10.3969/j.issn.1007-290X.2016.08.008

TM614

A

1007-290X(2016)08-0038-07

杜晓岩(1991)，男，河北石家庄人。在读硕士研究生，主要研究方向为风力发电和电机控制。

尹华杰(1966)，男，湖南洞口人。教授，工学博士，主要研究方向为特殊电动机的设计和电气传动控制。

叶超(1991)，男，河南南阳人。在读硕士研究生，主要研究方向为新能源并网技术。