基于高斯核函数的变分水平集模型研究及应用*

许法强，潘修强（浙江工贸职业技术学院信息传媒分院，浙江温州325003）

基于高斯核函数的变分水平集模型研究及应用*

许法强，潘修强
（浙江工贸职业技术学院信息传媒分院，浙江温州325003）

基于测地线活动轮廓（GAC）模型的变分水平集方法在图像分割领域目前应用较多，但其结果会受到图像边缘因子g的影响，基于这一点考虑引入了高斯核函数的平滑预处理，以减小其对曲线轮廓活动结果的影响。实验证明，该方法对两相灰度图像具有较好的分割效果。

GAC模型；变分水平集方法；高斯核函数

0　引言

图像分割是图像分析和计算机视觉研究的关键步骤，其目的是将图像划分为若干个不同的区域，每个区域包含了某个具有分割意义的对象。许多成功的图像分割方法都用到了基于偏微分方程（PDE）和变分水平集的模型。基于PDE模型的演化方程通常都是由最小化问题直接或间接引申而来，而变分水平集模型则是由定义于水平集函数上的能量泛函最小化问题直接推导而来的。

迄今为止已有很多针对基于PDE模型的研究［1］，本研究项目则主要集中于基于变分水平集模型的图像分割基础研究。已有的大量模型都取得了较好的分割效果［2］，但由于相关能量泛函易陷入局部极值点，导致活动轮廓的演化过程也会出现一些意外状况。在这些变分水平集模型中，我们必须提到Chan和Vese所提出的最常用的两相图像分割模型之一——无边缘活动轮廓模型［3］。

1　基于高斯核函数的图像分割方法

水平集函数实质就是用于表达一组无边缘界面集的Lipshitz连续函数。在二维空间中表示一组封闭曲线集，而在三维空间中则是一组无边缘的封闭二维曲面集。当使用水平集函数来描述一个动态界面时，相关的图像分割方法便称为水平集方法。

变分方法将图像分割视为一个优化问题的求解。首先在分割平面上形成一个泛函，为能正确确定该泛函形式，需要给良好分割结果赋予小的权值，而给不良分割结果则赋以大的权值，其次该泛函必须是连续函数。通用的泛函形式一般见式（1）：

之所以选用该形式，是因为它采用了变分公式来处理。一旦确定了泛函形，就能通过求导计算标定系列极值点，进而根据梯度下降算法处理得到一个最优点。

1.1水平集方法

为获取动态界面Γ，利用一个水平集函数来表示界面，然后根据一个分时偏微分方程即水平集公式来推导水平集函数ψ［4］。

定义1（水平集公式）：假设ψ：Ω→R为一代表界面Γ的水平集函数，则有如下关于值域为Ω的水平集函数ψ的水平集公式。

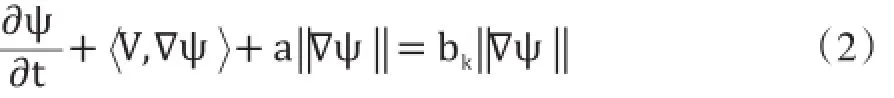
其中左边的第二项称为水平相对位移、第三项称为传播位移，公式的右边项则表示扩散位移。定义（1）通过简化参数V、a、b还能进一步演化，当维持水平集函数ψ为一个有符距离时，上述定义可以表示为如下定理所示的特定形式。

定理1（有符距离水平集公式）：假设ψ：Ω→R代表一个有符距离函数，则有如下等效于公式（2）的方程式：

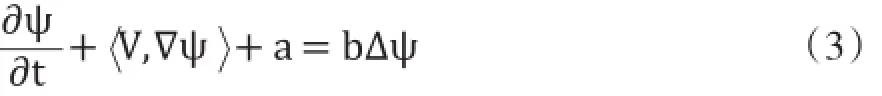
若公式（2）左边的第二和第三项忽略不计，则其还可进一步推导为如下形式，这取决于ψ是否能维持一个有符距离函数。

若公式（2）左边的第三项和右边项忽略不计，则又可进一步推导为如下形式，这便是著名的水平位移公式。

若公式（2）左边的第二项和右边项忽略不计，则还可进一步推导为如下形式，这同样取决于ψ是否能维持一个有符距离函数。通过这种降阶方法，最终求取全局最优值。

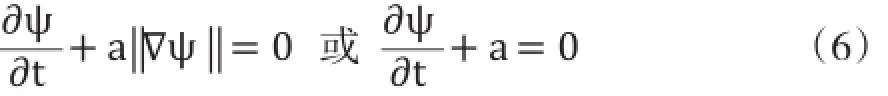
1.2变分方法

较早将变分方法应用于图像分割的研究者有Kass等人［5］，在其论文中通过构造的样条函数来描述对象边界。该函数中包括仅依赖于样条曲线的的正则项、依赖图像的梯度变化项、张力和斥力等用户输入项。他们通过该函数推导出相应的Euler-Lagrange公式，并用这些公式来求解一个梯度下降的稳态系统问题。

在该类众多的数值求解方法中，最著名的就是Chan-Vese的分段常量式Mumford-Shah模型［3］，即变分水平集模型：

Chan和Vese假设Ω表示平面图像域，I则代表该域内的一幅给定图像，那么Chan-Vese模型可以表达为公式（8）能量泛函的最小化问题。

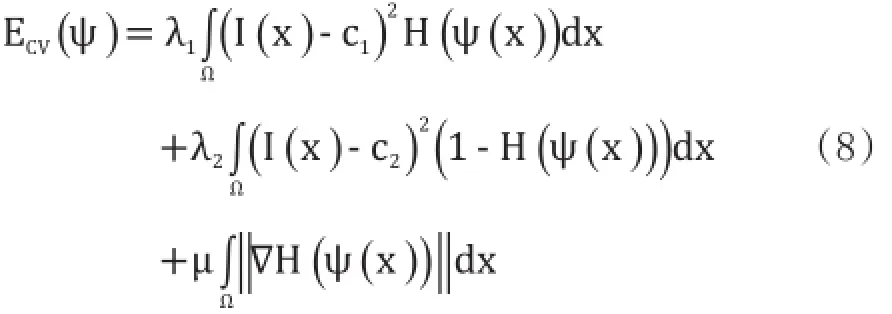
其中，λ1、λ2和μ均为正参数，ψ为一水平集函数，H则代表一个如公式（9）定义的Heaviside函数。

而两个分段常数c1和c2则分别按公式（10）来确定。

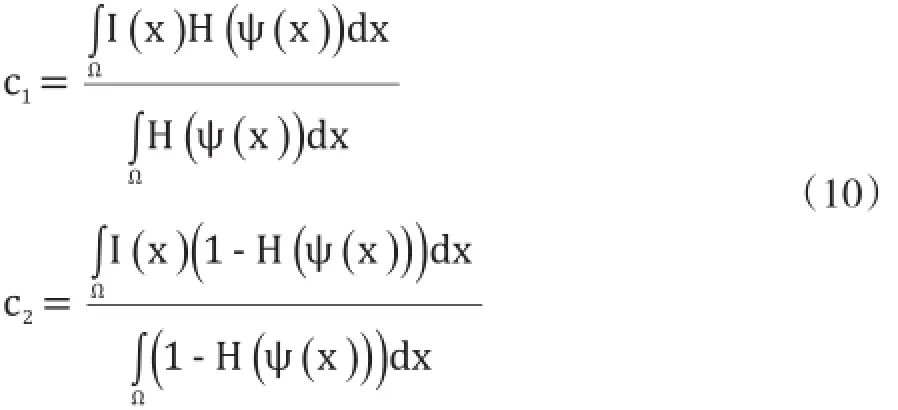
它们分别代表了图像I在Ω1和Ω2域内的平均像素值，其中：

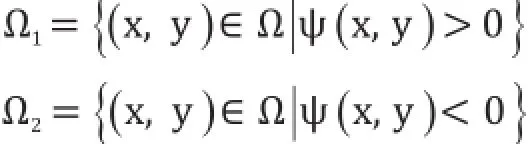
1.3基于高斯核函数的变分水平集模型

测地线活动轮廓（GAC）模型是目前水平集方法在图像分割领域推广应用较多的模型之一［6-7］。该模型认为曲线运动受到两个方面的影响，第一个方面来自于曲率几何形变，第二个方面则来自于图像边缘函数g的梯度变化，其中前者也会受到后者当中因子g的影响。这两个方面的因素吸引着曲线向边界方向靠拢，从而最终达到最佳稳态。

在上述处理过程中，为了获取更为精确的图像边缘函数g，我们对待分割图像额外进行了高斯平滑预处理，以减小边缘因子对曲线轮廓活动结果的影响，使之尽快达到稳定状态进而停止迭代。高斯核函数是一种最常用的径向基函数，其一般形式为：

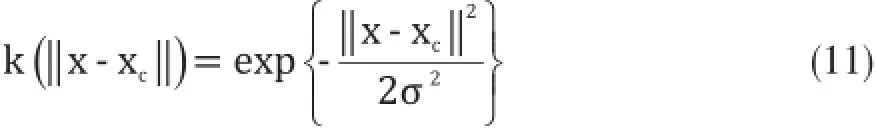
其中，xc代表核函数中心点，σ为控制函数径向作用范围的宽度参数。

2　实验结果

本文为了方便处理和验证算法，将待分割图像暂时限定为宽高等比例的两相灰度图像。其处理过程如下：首先，将输入图像转为灰度图，并适当调整图像大小至宽高相等；其次，利用高斯核函数对灰度图像进行一维和二维卷积的预平滑处理，高斯核大小取3、高斯函数的方差取2；再次，计算图像梯度值，及初始化封闭曲线为图像的内切圆（即零水平集）并以此初始化水平集函数；最后，按采用GAC模型的变分水平集方法的单边迎风方案进行迭代处理，迭代次数的上限设为4 000次、迭代步长为0.01、速度常数为3。对两组两相图像进行实验后的结果分别如下图1和图2所示，从中可以看出本文处理方法的可行性。

图1　第一组原始图像、叠加零水平集后的图像、最终分割图像

图2　第二组原始图像、叠加零水平集后的图像、最终分割图像

3　结论

文章提出了一种基于高斯核函数的变分水平集模型，并将其成功应用于两相灰度图像的分割任务中。该模型考虑了边缘停止函数g对曲线轮廓“靠边”运动的影响，从而利用高斯核函数对灰度图像做高斯核卷积计算以达到预平滑目的。最终通过两组两相图像的分割实验，证明了该方法能在较短时间内取得不错的分割效果。

［1］K.Zhang，L.Zhang，H.Song，D.Zhang.Re-initialization Free Level Set Evolution via Reaction Diffusion［J］.IEEE Trans.Image Process，2013，22（1）:258-271.

［2］S.Liu，Y.Peng.A LocalRegion-based Chan-VeseModelfor Image Segmentation［J］.Pattern Recognition，2012，45:2769-2779.

［3］T.F.Chan，L.A.Vese.Active ContourswithoutEdges［J］.IEEETrans.Image Process，2001，10（2）:266-277.

［4］Stanley J.Osher，Ronald P.Fedkiw.Level Set Methods and Dynamic Implicit Surfaces［M］.New York:Springer-Verlag Inc.，2002: 20-24.

［5］Michael Kass，Andrew Witkin，Demetri Terzopoulos.Snakes:Active Contour Models［J］.International Journal of Computer Vision，1987，1:321-331.

［6］刘玉，王浩然，张秀林，安然.一种改进的GAC模型图像分割算法［J］.伺服控制，2014（5）:59-61.

［7］吴继明.基于水平集方法的主动轮廓模型理论研究及其应用［D］.华南理工大学，2010.

（责任编辑：梅成才）

Research on Gaussian Kernel-based Variant LevelSetModeland ItsApp lication

XU Fa-qiang，PAN Xiu-qiang
（Collegeof Information and Communications，Zhejiang Industry&Trade VocationalCollege，Wenzhou，325003，China）

Geodesic active contour（GAC）model-based variant level setmethod iswidely used to image segmentation recently，but itwould result from the image edge factor，g.Therefore the Gaussian kernel function is introduced to pre-smooth the given image，which could reduce the effectof g to the active curve contour state.The experiments prove that the abovemeans is provided with the preferable resultaiming at the two-phasegray image.

geodesic active contourmodel；variant levelsetmethod；Gaussian kernel function

TP391

A

1672-0105（2016）01-0034-03

10.3969/j.issn.1672-0105.2016.01.009

2016-03-19

2014年浙江工贸职业技术学院学术委员会课题“图像分割关键技术研究”（XW1402）

许法强，博士，浙江工贸职业技术学院讲师，主要研究方向：图像传播工程；潘修强，硕士，浙江工贸职业技术学院副教授，主要研究方向：数字图像处理。