大型振动台结构设计中的有限元分析与应用

刘明辉，王 剑，高海洋，岳志勇，张俊刚



大型振动台结构设计中的有限元分析与应用

刘明辉，王 剑，高海洋，岳志勇，张俊刚

（北京卫星环境工程研究所，北京100094）

振动台是振动试验系统的主体结构。文章以某大型振动台结构设计为例，探讨了有限元法在振动台结构设计中的应用。工程实践表明，有限元法在大型振动台结构分析设计中，可以解决复杂结构的力学计算问题，有助改进结构设计，提高振动台结构的合理性和可靠性。

有限元方法；振动台；结构设计；模态；频率响应

0 引言

航天器的大型化对振动台技术的要求越来越高。各航天大国和机构均非常重视大型振动台的研制。欧空局研制了由4台激振器并联的64t垂直振动台，美国、日本、俄罗斯等国均建立了各自的航天器大型振动台。我国振动台的研制起步滞后于发达国家，但近年来也取得了显著成果，研制了70t电动振动试验系统并应用于火箭仪器舱振动试验[1]。

大型振动台主要由台面、支撑结构、导向机构等部分组成，构成复杂，在设计中需要开展非常精细的计算和结构的静动特性的全面分析，以确保系统设计的合理性。有限元分析方法在各类工程结构设计中具有广泛的应用，并发挥着重要的作用[2-4]。苏嵩、夏天凉等[5-6]采用有限元分析方法对振动台的附加台面结构进行了优化设计，验证了分析方法的正确性。范宣华、张逸波等[7-8]给出了电动振动

台动圈有限元建模方法，并进行了模态和振动响应仿真分析，经模型修正后的预示结果与试验结果基本吻合。徐文正等[9]介绍了有限元分析方法在三轴六自由度振动台设计中的应用，研究指出该方法可以为振动台的设计提供良好的技术支撑。然而，已开展的研究主要针对振动台附加台面、动圈等单体结构以及单激振器小型振动台，尚未开展大型振动台结构的分析研究。

本文针对大型多激振器并联振动台结构的设计，采用有限元分析方法，对振动台结构刚度、强度和动力学响应特性进行了分析，并在结构设计过程中开展了系统特性预估，就预估中所暴露的设计问题，完成了结构方案的改进设计，从而使大型振动台的设计更趋合理。

1 大型振动台结构组成

某大型垂直振动台是由4台激振器并联构成

的系统，主要由激振器台体和动圈、台体支撑结构、扩展台、扩展台导向轴承、扩展台支撑结构以及空气弹簧等组成，如图1所示。该振动台的最大正弦推力1400kN，总体包络尺寸约8000mm（宽）×3500mm（高）。扩展台面尺寸约4000mm×4000mm，其导向轴承采用预加载式和被动式轴承对，预加载达200kN。台体和扩展台导向支撑结构采用Q235B钢，扩展台面的材料为镁合金。大型振动台结构设计需要综合考虑试验需求、使用环境、各部件的性能，以及振动台系统性能。本文针对该振动台的结构设计方案开展了有限元分析，包括振动台的模态、静动载荷以及频率响应。

图1 多激振器并联大型垂直振动台结构主要组成示意图

2 模态分析

图2所示为垂直向振动台的模态对试验件振动试验的影响。理想情况下，试验件固支在振动台台面上，当振动台受动圈激励时，在一定的频率范围内产生特定量级的垂直向振动，使试验件按图2(a)情况振动。然而，由于振动台结构自身的刚度，特别是相对地面的连接刚度，使得振动台不能按理想的情况运动，而是有一定的“摇摆”模态

（见图2(b)）。

(a) 理想情况 (b) 实际情况

对于小型振动台，其结构的刚度较大，则“摇摆”频率可以设计得较高，甚至高于试验频率范围；而对大型振动台则很有可能无法实现。在振动台结构有限元设计分析时，除了对构成结构部件的精确建模之外，还需要重点对其模态进行设计分析，特别要关注扩展台面质量、扩展台支撑结构刚度以及扩展台导向轴承刚度等因素的影响。

依据振动台初步设计的结构方案，在MSC. Patran软件平台上建立该方案的有限元分析模型。扩展台、支撑结构等为板式组合结构，它们的建模可采用板壳单元。由于扩展台导向轴承约束横向运动，可采用弹簧单元对横向约束刚度建模，弹簧刚度参数可根据轴承真实刚度设置，所选型号轴承刚度为1.6×1010N/m。激振器动圈为刚度较大的实体结构，因此采用集中质量单元建模；动圈径向运动采用静压轴承和摇臂滚装置进行约束，因此径向刚度采用弹簧单元建模，根据激振器设计结果，其径向刚度为4.4×108N/m。空气弹簧简化为弹簧单元，其刚度参数与充气压力有关，本文中振动台为空载，空气弹簧充气后刚度为1.97×105N/m。激振器台体和台体支撑结构刚度较大，且振动试验过程中不参与运动，简化为固支边界。所有焊接和螺栓均按固接处理。采用自动与手动相结合的方法进行网格剖分。主要材料特性见表1。

注：焊接接头疲劳强度与接头类型有关。

对初步设计振动台结构的模态分析可知，其一阶摇摆模态频率36Hz，如图3(a)所示。可见一阶摇摆频率较低，振动试验时容易发生振动台与试验件的耦合，不利于振动试验控制，需要进行改进设计。利用有限元分析结果，识别出初步设计振动台中的扩展台导向支撑结构刚度较弱。通过对该支撑结构的改进设计，其刚度得到了提高，质量增加约20%，一阶摇摆模态频率提升至52Hz（提高了44%），其模态如图3(b)所示。因此，应用有限元法对振动台结构进行模态分析，可有效指导降低

振动台结构与试验件的耦合，有助于提高振动试验控制精度。

(a) 初步设计（36Hz）

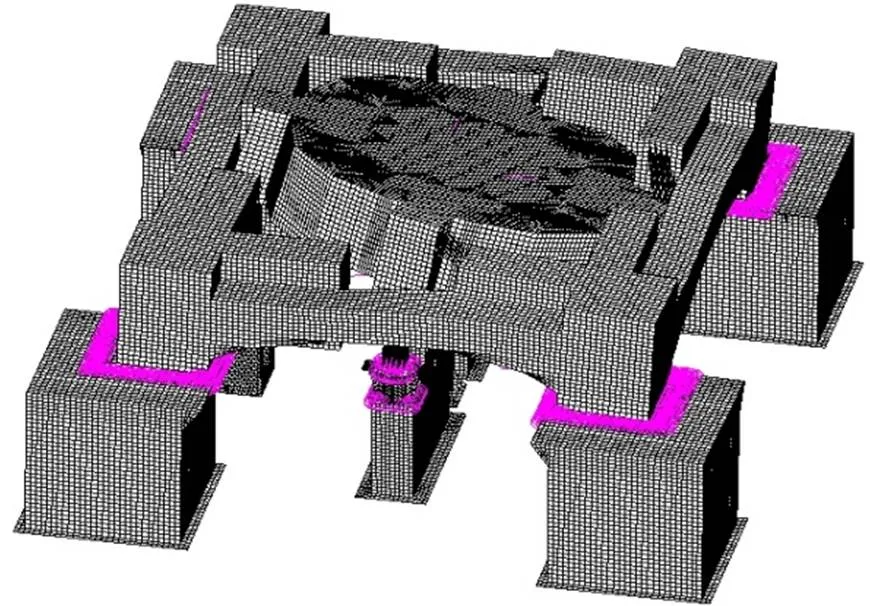
(b) 改进设计（52 Hz）

3 静动载荷分析

振动试验前，首先需要测试振动台结构对试验件的静承载是否满足静强度要求。静承载主要由扩展台、空气弹簧及支撑结构承担，并经由这3个结构部件传递至地面。通常，振动台结构的静强度可以设计得具有较大安全裕度。

在动载荷作用下，振动台结构需要满足动强度要求。振动试验时，动圈把推力传递给扩展台。由于试验件存在质心偏心，振动时会产生倾覆力矩载荷，并通过扩展台传递至导向轴承、支撑结构，最终传递至地面。大型扩展台结构通常采用焊接成型，焊接处容易产生应力集中，动强度分析时需要重点校核。动强度校核应以焊接接头疲劳强度为参考值。同时，由试验件质心偏心产生的倾覆力矩致使扩展台面和导向轴承发生弹性变形。导向轴承是关键部件，其导向精度极高，变形过大会导致轴承卡死，进而无法进行振动试验；因此需要根据导向轴承的真实刚度参数，进行局部的变形分析，确保轴承变形满足导向要求。有限元分析时最大动载工况采用满额推力和最大抗倾覆力矩设计值的组合作为工作载荷进行分析计算。

大型振动台结构承载需求大，且结构复杂，因此需采用有限元法对其强度和变形进行校核。按最大设计静载40t并考虑结构自重载荷，加载后扩展台最大应力仅5.45MPa，该应力所对应的位置在导向轴承下板空气弹簧对接位置处，如图4(a)所示。支撑结构中，最大应力发生在空气弹簧的支撑结构上，最大应力值为28.2MPa。可见，系统结构静强度安全裕度很大。

按满额推力1400kN和最大倾覆力矩240kN·m进行加载，则扩展台最大应力为15.5MPa，所对应的位置在扩展台上端轴承安装面处，如图4(b)所示，其疲劳强度安全系数3.7。位于动圈安装位置对应的扩展台内部的竖立筋板与扩展台底板对接处的最大应力达6.9MPa，按焊接疲劳强度校核，其安全系数为2.5。扩展台面支撑结构的最大应力值为29.7MPa，远未达到表1中钢的屈服强度指标，因此满足动强度要求。

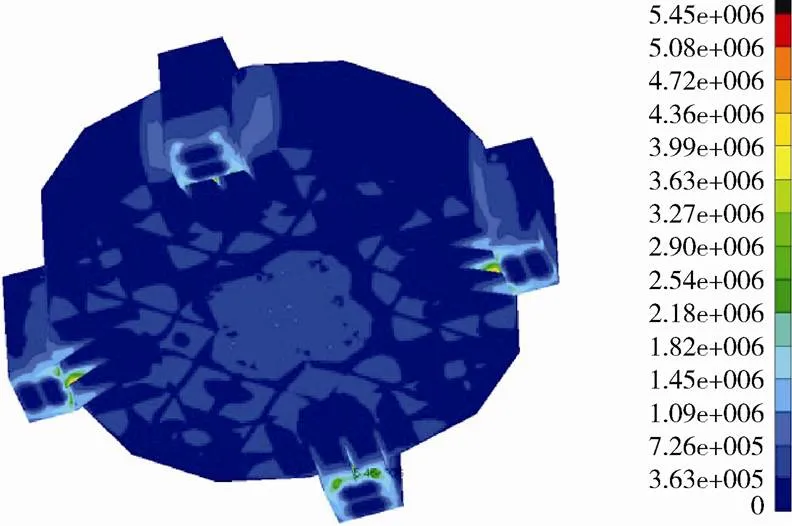
(a) 静载工况

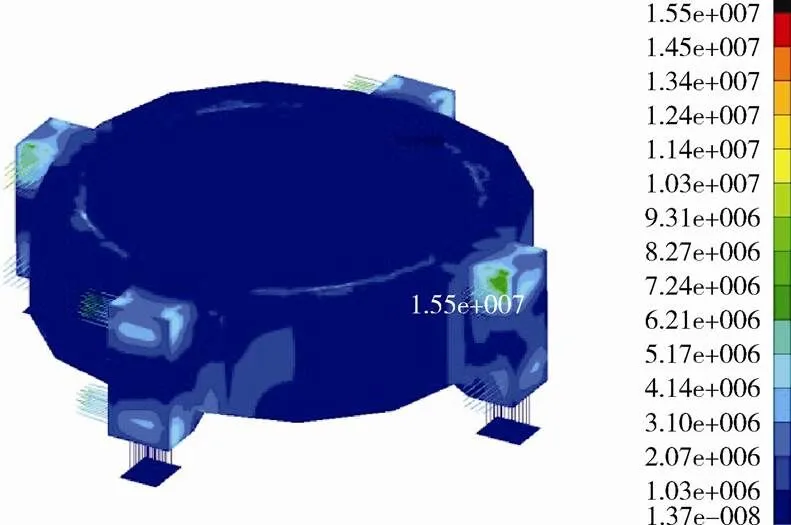
(b) 动载工况

在最大动载作用下计算轴承安装面的位移，得到导向轴承安装面的绝对变形最大值为0.005mm，如图5所示，这满足轴承变形小于0.01mm的指标要求，因此扩展台可沿导向轴承正常运动。

图5 导向轴承变形云图

4 频率响应分析

振动台结构的频率响应特性是指扩展台面振动相对动圈激励运动的传递特性，是衡量激励传递和结构动态特性的重要指标。振动台动圈的激励通过刚度较大的转接锥结构传递给扩展台，而扩展台由于自身的结构刚度使台面上的点产生振动放大、横向分量以及不同位置的不均匀振动。随着扩展台面尺寸增大和结构复杂，其结构模态将密集化，频率响应特性也变得更复杂。这些频率响应特性是影响振动试验控制精度的重要因素，在试验频率范围内，振动台结构特别是扩展台结构的频率响应特性应尽量光滑平直，对于大型扩展台面，还应使其不同位置的频率响应特性尽量均匀一致。频率响应特性的设计重点是扩展台面的动力学特性，可以通过台面主振方向振动传递特性、台面振动幅值均匀度以及台面横向振动比等参数评价振动台结构的频率响应特性[10]。

本文所设计的振动台为4台激振器同步激励（即同幅值和同相位），即在4个动圈上施加单位量级同步的加速度激励载荷，通过计算扩展台面上的加速度响应，进行振动台结构的频率响应分析。在扩展台面上中心、中环、外环、动圈对应位置以及导向轴承安装位置等处布置了测点，如图6所示。

扩展台面中心测点所获得的主振方向振动传递特性如图7所示，在225Hz和310Hz处有峰值，响应放大较大，究其原因主要是扩展台的一阶和二阶弯曲模态导致台面产生共振，如图8所示。

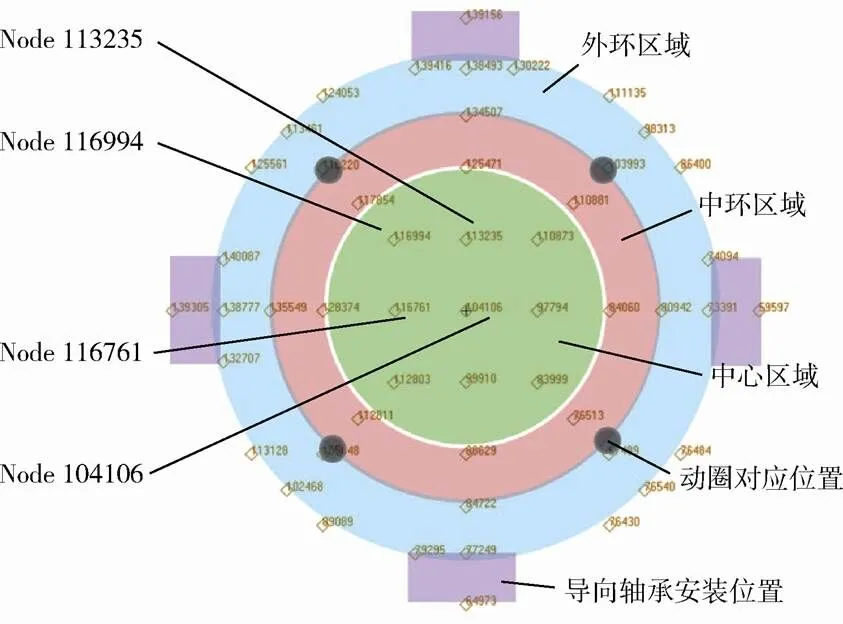
图6 频率响应分析测点位置

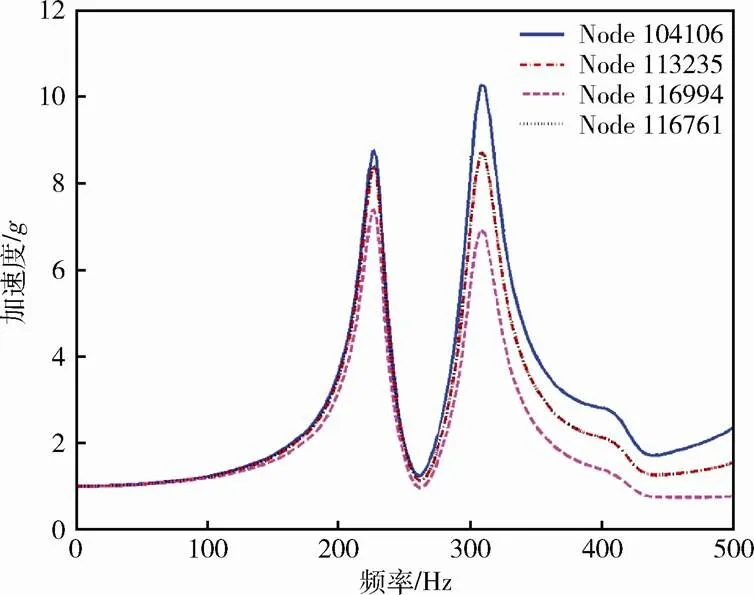
图7 扩展台面中心区域主振方向振动传递特性

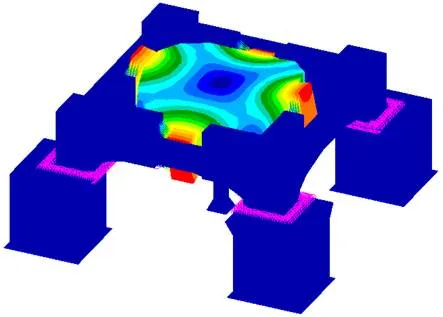
图8 系统结构中扩展台面的一阶、二阶局部模态

将扩展台面不同测点的振动传递特性与中心测点的振动传递特性比较，以计算出台面振动幅值不均匀度。根据计算结果，5～100Hz频段内台面上动圈对应位置和台面中环测点的幅值不均匀度在12.3%以内，达到了JJG 948—1999的A级标准。其中幅值不均匀度，式中：为同次测量中中心测点的加速度幅值；|Δmax|为同次测量中，各测点加速度值与中心测点加速度幅值的最大偏差。

扩展台面横向振动特性如图9所示。根据计算结果，100Hz处台面中心测点横向振动比最小为0.05%，轴承安装位置附近横向振动比最大为3.5%，均达到JJG 948—1999的A级标准。其中横

图9 扩展台面横向振动特性

5 结束语

本文论述了有限元法在大型振动台结构设计分析中的应用。随着航天技术的发展，振动台越来越大型化，结构愈加复杂，利用有限元法对振动台结构设计进行分析和改进，可以使设计更趋合理。目前，本文实例中的大型振动台系统已建造完成，并进行了调试测试，后续将通过试验对有限元分析结果进行验证和修正，进一步完善有限元法在大型振动台结构设计中的应用。

（References）

[1] 国内最大推力振动试验系统成功应用于CZ-5火箭研制[J]. 生命科学仪器, 2012(5): 50

[2] 韩潇, 祁妍. 大型真空容器结构设计中的有限元分析与应用[J]. 航天器环境工程, 2009, 26(2): 150-153

Han Xiao, Qi Yan. Finite element analysis in the design of large vacuum chamber[J]. Spacecraft Environment Engineering, 2009, 26(2): 150-153

[3] 梁天也, 史文库, 马闯. 汽车动力总成液压悬置橡胶主簧静特性有限元分析[J]. 振动与冲击, 2007, 26(9): 155-157

Liang Tianye, Shi Wenku, Ma Chuang. Finite element analysis of static characteristics of main rubber spring for a hydraulic engine mount[J]. Journal of Vibration and Shock, 2007, 26(9): 155-157

[4] 王兴刚, 姜年朝, 张逊, 等. 某无人机复合材料机翼有限元分析[C]∥第19届全国结构工程学术会议. 济南, 2010: 482-485

[5] 苏嵩, 陈红光, 郁林聪. 高频电液振动台用台面的性能分析及优化设计[J]. 液压与气动, 2009(2): 19-21

Su Song, Chen Hongguang, Yu Lincong. Design optimization and analysis of head expander for high-frequency electro-hydraulic vibration generator[J]. Chinese Hydraulics & Pneumatics, 2009(2): 19-21

[6] 夏天凉, 王金娥, 卢华强, 等. 电动振动台附加台面的结构分析及其优化设计[J]. 苏州大学学报（工科版）, 2011, 31(3): 49-54

Xia Tianliang, Wang Jin’e, Lu Huaqiang, et al. Structural analysis and optimal design of electrodynamic vibrator appending table[J]. Journal of Suzhou University (Engineering Science Edition), 2011, 31(3): 49-54

[7] 范宣华, 胡绍全. 电动振动台空台建模与仿真技术研究[J]. 系统仿真学报, 2006, 18(2): 313-315

Fan Xuanhua, Hu Shaoquan. Modeling and simulation research on electrodynamic vibration generators[J]. Journal of System Simulation, 2006, 18(2): 313-315

[8] 张逸波, 齐晓军, 张丽新. 200kN振动台动圈建模与仿真分析[J]. 航天器环境工程, 2009, 26(3): 244-247

Zhang Yibo, Qi Xiaojun, Zhang Lixin. Modelling of armature of 200kN shaker and its simulation[J]. Spacecraft Environment Engineering, 2009, 26(3): 244-247

[9] 徐文正, 孙建勇. 有限元分析在三轴六自由度振动系统设计中的应用[J]. 装备环境工程, 2011, 8(1): 21-28

Xu Wenzheng, Sun Jianyong. Application of virtual vibration test technique in building three-axis six degrees of freedom vibration test system[J]. Equipment Environmental Engineering, 2011, 8(1): 21-28

[10] JJG 949—1999 数字式电动振动试验系统检定规程[S], 1999

（编辑：许京媛）

Application of FEA in structure design of large vibration test bed

Liu Minghui, Wang Jian, Gao Haiyang, Yue Zhiyong, Zhang Jungang

(Beijing Institute of Spacecraft Environment Engineering, Beijing 100094, China)

The vibration test bed is the main structure of a large vibration test system. For a typical large vibration test bed, the finite element analysis method is applied for the structural design of the test bed. It is concluded that the finite element analysis method can be used for a complex structure, and for optimizing the structure to improve the rationality and reliability of the test bed.

finite element method; vibration test bed; structure design; mode; frequency response

V416.2

A

1673-1379(2016)03-0257-05

10.3969/j.issn.1673-1379.2016.03.005

刘明辉（1982—），男，博士学位，主要从事航天器力学环境试验研究工作。E-mail: liuminghui.china@163.com。

2015-12-04；

2016-04-20

载人航天工程三期

http://www.bisee.ac.cn E-mail: htqhjgc@126.com Tel: (010)68116407, 68116408, 68116544