基于微粒群算法的海堤渗压RBF神经网络监测模型

闫彭彭，黄　铭

(1.合肥工业大学土木与水利工程学院，安徽合肥230009；2.三峡库区地质灾害教育部重点实验室(三峡大学)，湖北宜昌443000)



基于微粒群算法的海堤渗压RBF神经网络监测模型

闫彭彭1，2，黄铭1，2

(1.合肥工业大学土木与水利工程学院，安徽合肥230009；2.三峡库区地质灾害教育部重点实验室(三峡大学)，湖北宜昌443000)

为提高海堤安全监控能力，从渗压实测数据以及潮位因子和降雨因子入手，使用影响因子的合理形式，利用径向基函数(RBF)神经网络建立渗压监测模型，推导微分进化微粒群优化算法(DPSO)速度和位移进化的数值计算方程，以此确定渗压RBF神经网络模型的聚类中心，并由此对渗压进行拟合和预测。以120组实测样本对模型进行训练拟合，并对后期60组渗压进行预测，得到拟合段平均相对误差为0.83%，相应预测段为1.71%。实际应用表明，经微分进化微粒群算法优化后，渗压RBF神经网络模型可以有效反映及预测渗压变化。

海堤；渗压监控；径向基函数；微分进化；微粒群优化

海堤是以土石材料为主、沿海而建、防潮挡浪的特殊水工建筑物，有针对地加强对海堤的安全监控十分必要[1]。渗压是反映海堤安全状态的重要参数，并且可以获取稳定、连续的监测资料。海堤渗压受到诸如潮水位、降水、台风及波浪等因素的影响[2]。本文从渗压实测数据及影响渗压的主要环境量(潮水位、降雨)出发，通过分析，选择合理的影响因子，借助径向基函数(Radial Basis Function，RBF)神经网络，建立海堤渗压监控因果模型。利用微粒群优化(Particle Swarm Optimization,PSO)算法优化聚类中心，从而提高模型拟合及预测效果。

1　渗压RBF神经网络监测模型

RBF神经网络是一种前馈型的非线性网络[3- 4]，因其较快的收敛速度和较强的学习能力而被广泛运用。RBF神经网络一般为“输入层—隐含层—输出层”结构。对于有m个输入、n个输出、K个隐含单元的RBF网络输出为

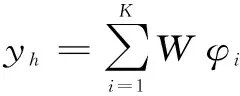
(1)

确定渗压神经网络监测模型聚类中心的方法主要有K-均值算法、C-均值算法和模糊C-均值算法等。其中，K-均值算法和C-均值算法较为简单，在一定的条件下收敛较快，能获得相对理想效果。但这2种方式也存在一定的缺陷[5- 6]，使其推广受到制约。模糊C-均值算法[7- 8]引入模糊数学原理，改善了对样本集分类时任意子样本完全隶属于某个分类的不足，提出模糊分类的概念，即子样本可同时对不同聚类中心做出贡献，这种方式在确定RBF网络聚类中心时更为合理。对于海堤渗压的RBF神经网络监测模型，在确定聚类中心后，以实测样本对集{X，Y}为模型的输入与期望输出，利用最小二乘回归计算权值矩阵W，再将聚类中心和连接权值代回式(1)，实现对渗压的拟合和预测。然而，初始聚类中心的确定对RBF神经网络的性能具有决定性作用。如果不能合理的选取初始聚类中心，渗压监测模型的效果会大大降低甚至失效。

为降低聚类中心初始化过程对神经网络模型的影响，本文采用算法思路较为简单且通用性、鲁棒性较强，收敛较快的微粒群优化算法来搜索、优化RBF神经网络的聚类中心。同时，为提高优化结果，避免算法过早收敛，在建立海堤渗压的监测模型时，采用了微分进化的微粒群优化(PSO)算法。

2　微粒群优化(PSO)算法优化渗压监测模型

PSO是一种基于社会影响和社会学习而提出的群体智能算法。对于有M个种群的标准微粒群算法[9- 12]的速度进化方程和位置进化方程分别为

(2)

种群i的历史最优位置表示对种群i此前各代的搜素中获得的最优位置，更新方式如下

(3)

式中，f(·)为适应值函数。针对本文采用的海堤渗压径向基函数神经网络监测模型，选择全局误差平方和函数作为PSO算法的适应值函数。

群体历史最优位置表示对所有种群此前各代的搜索中获得的全局最优位置，更新方式如下

(4)

为降低标准微粒群算法采用固定步长对计算结果的影响，引入利用具有绝对稳健性进行步长选择的微分进化微粒群(Differential Evolutionary Particle Swarm Optimization,DPSO)算法[13]

(5)

式中，φ1=a1r1;φ2=a2r2;φ=φ1+φ2。

采用能够提高精度、避免过早收敛且相对简单的二阶Runge-Kutta法进行插值计算。通过推导可以得出第k+1代位置向量与第k代位置向量的关系为

(6)

式中，b为步长，可按文献[13]推荐值进行计算

(7)

用DPSO算法优化RBF网络模型参数时，定义微粒群位置向量的元素分别是RBF网络模型的聚类中心。基本步骤如下：

(1)构建海堤渗压RBF网络监测模型，确定网络的输入、输出以及隐含层节点个数等要素。

(2)根据渗压分布规律及相关经验，初始化位置向量、速度向量；设定速度上限、最大进化代数T以及迭代精度，并令此时进化代数为0。

(3)取适应值函数f为全局误差平方和

(8)

(4)确定种群各维分量微分进化时的步长。

(5)将各种群位置转换成RBF网络聚类中心，将实测样本对集代入网络模型，并计算当前适应值。

(6)根据式(3)计算各种群历史最优位置，根据式(4)确定群体最优位置，根据式(6)计算下一代微粒群位置。

(7)计算相邻步适应值之差，并更新各种群的历史最优位置和群体的历史最优位置。

(8)根据模型要求设定迭代条件，若达到结束条件，停止迭代并输出最优结果；否则返回第(4)步。

3　实例分析

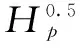
降雨对土石体的结构状态具有重要影响。海堤处于频繁、高强度降雨的特殊工作环境，因此必须特别重视降雨对海堤安全的影响。考虑到降雨入渗的滞后性以及入渗能力的有限性，本文采用降雨的积分形式作为监测模型的影响因子[15]。其基本形式为

(9)

式中，R为降雨因子；t为当前时刻；τ为此前任意时刻；Iτ为τ时刻的降雨强度，如果Iτ大于入渗能力Ip，则取Iτ=Ip；φ(·)为降雨作用函数，可参考相关工程经验选取。对降雨因子的积分求解，利用数值积分进行插值计算。

构建海堤渗压监控RBF网络模型，并利用微分进化的DPSO算法优化网络，从而构建海堤渗压DPSO-RBF网络监测模型。以浦东海堤某断面实测渗压值作为期望输出，以前期潮位因子和降雨因子作为网络输入，以实测数据形成的120个训练样本对网络模型进行训练，并对后期60个渗压进行预测。模型拟合效果见图1。模型误差分布见图2。

图1　模型拟合效果

图2　模型误差分布

从图1、2可知，经DPSO优化RBF网络聚类中心的监测模型拟合效果比较理想，其拟合值与对应实测值的最大绝对误差为0.059，最大相对误差为1.89%，平均相对误差为0.83%；并且，DPSO-RBF网络监测模型也展现了更强的预测能力，将后期60个渗压预测值与对应实测值比较，其最大绝对误差为0.065，预测的最大相对误差为2.33%，预测平均相对误差为1.70%。表明经微分进化PSO算法优化的RBF网络监控模型可以有效反映海堤渗压变化规律，监控效果能够得到保障，并且能够实现对渗压高精度的预测。考虑到渗压实测资料具有实时性以及本文建立的渗压监测模型在60 h内(即60个渗压序数)的预测效果已经满足精度要求，因此在实际工程中只需不断更新监测资料，以最新监测数据作为输入，实现对海堤渗压的有效监控、预测。

4　结　语

本文根据海堤渗压的特殊规律，利用非线性映射能力较好的RBF网络建立海堤渗压监控模型，以渗压监测资料作为模型的输出，以对应的主要影响因素的合理形式作为模型的输入，并以微分进化微粒群优化(DPSO)算法对RBF网络的聚类中心进行搜索、优化，构建基于微分进化微粒群算法优化径向基神经网络的海堤渗压监控模型。

实际训练结果表明，DPSO-RBF网络模型可以准确地反映海堤渗压的规律，并且能够对其进行可靠预测，为海堤安全监测工作提供有效分析工具。

[1]秦植海， 秦鹏. 海堤地基固结系数反演与工后沉降分形模型预测[J]. 岩土力学， 2012， 33(6)： 1747- 1753．

[2]唐巨山， 袁文喜， 曾甄. 海堤堤顶高程确定中若干问题的探讨[J]. 水力发电， 2008， 34(2)： 39- 42．

[3]薛晓岑， 向文国， 吕剑虹. 基于差分进化与RBF神经网络的热工过程辨识[J]. 东南大学学报： 自然科学版， 2014(4)： 769- 774．

[4]乔俊飞， 韩红桂. RBF神经网络的结构动态优化设计[J]. 自动化学报， 2010， 36(6)： 865- 872．

[5]王汉芝， 刘振全. 一种新的确定K-均值算法初始聚类中心的方法[J]. 天津科技大学学报， 2005， 20(4)： 76- 79．

[6]单凯晶， 肖怀铁. 初始聚类中心优化选取的核C-均值聚类算法[J]. 计算机仿真， 2009， 26(7)： 118- 121．

[7]朱然， 李积英. 几种优化FCM算法聚类中心的方法对比及仿真[J]. 计算机技术与发展， 2015， 25(5)： 17- 20．

[8]黄铭， 刘俊. 深基坑开挖位移多点监测模型及径向基函数神经网络计算中心的FCM确定[J]. 工业建筑， 2012， 42(3)： 80- 83， 158．

[9]陈国初， 俞金寿. 微粒群优化算法[J]. 信息与控制， 2005， 34(3)： 318- 324．

[10]KENNEDY J， EBERHART R C. Particle swarm optimization[C]∥Proceeding of 1995 IEEE International Conference on Neural networks. New York： IEEE， 1995， 1942- 1948．

[11]王行甫， 陈宏亮. 基于改进粒子群优化算法的BP预测模型[J]. 计算机系统应用， 2014， 23(4)： 135- 137， 143．

[12]虞英杰， 蒋卫刚， 徐明芳. 基于PSO算法的BP神经网络对水体叶绿素a的预测[J]. 环境科学研究， 2011， 24(5)： 526- 532．

[13]曾建潮， 崔志华. 微分进化微粒群算法及其控制[J]. 系统工程学报， 2007， 22(3)： 328- 332．

[14]黄铭. 潮位影响下的海堤渗压变化特点[J]. 人民长江， 2010， 41(6)： 26- 29．

[15]黄铭， 刘俊. 降雨影响下高边坡渗压神经网络监测模型[J]. 上海交通大学学报， 2013， 47(10)： 1548- 1551.

(责任编辑杨健)

Seawall Seepage Pressure RBF Neural Network Monitoring Model Based on Particle Swarm Optimization

YAN Pengpeng1, 2, HUANG Ming1, 2

(1. School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, Anhui, China;2. Key Laboratory of Geological Hazards on Three Gorges Reservoir Area (China Three Gorges University),Ministry of Education, Yichang 443000, Hubei, China)

In order to improve the monitoring capacity of seawall, a seepage pressure monitoring model based on radial basis function (RBF) neural network with reasonable forms of influencing factors is established based on observed seepage pressure data as well as tidal level data and rainfall factor data that influence seepage pressure. The numerical calculation equations of differential equations for speed and displacement evolution are derived, and the RBF centers are conformed by differential evolutionary particle swarm optimization (DPSO) to fit and forecast seepage pressure. 120 measured samples are used for fitting and training the monitoring model with average relative error of 0.83%, and the later 60 seepage pressure values are predicted with average relative error of 1.71%. The actual application shows that, after optimized by differential evolutionary PSO, the seepage pressure monitoring model can effectively reflect and predict the general law of seepage pressure．

seawall; seepage pressure monitoring; radial basis function; differential evolutionary; particle swarm optimization

2016- 01- 18

三峡库区地质灾害教育部重点实验室(三峡大学)开放研究基金项目(2015KDZ03)；水利部公益性行业科研专项经费资助项目(201401063- 02)

闫彭彭(1992—)，男，安徽阜阳人，硕士研究生，研究方向为水工建筑物安全监测；黄铭(通讯作者)．

TV698.12

A

0559- 9342(2016)05- 0099- 03