RPC抗折疲劳寿命的威布尔分布研究

杨科文，罗许国

(湖南科技大学 土木工程学院，湘潭 411201)



RPC抗折疲劳寿命的威布尔分布研究

杨科文，罗许国

(湖南科技大学 土木工程学院，湘潭 411201)

活性粉末混凝土(简称R.PC)是一种新型水泥复合基材料，由于具有超高强度、高韧性、高耐久性等优良性能而受到越来越多的学者的关注与研究，随着我们研究的逐步加深，RPC材料也会越来越多的被应用于实际工程中.通过三种不同钢纤维体积掺量的试件进行抗折疲劳试验,研究了RPC的疲劳寿命分布,疲劳试验获得了试件的抗折疲劳加载次数，并用疲劳统计学理论验证了RPC疲劳寿命的威布尔分布.

活性粉末混凝土；钢纤维；抗折疲劳试验；疲劳寿命；威布尔分布

0　引　言

RPC是19世纪20年代法国BOUYGUES公司研发出的一种新型混凝土.它具有超高的强度、较低的脆性、良好的韧性以及优异的耐久性能，具有广阔的研究开发与应用前景.RPC是由水泥、粉煤灰、石英砂、硅粉、高效减水剂等组成，并通过掺入钢纤维以提高RPC的延性和韧性[1-2].

与静载强度破坏机理相比，混凝土的疲劳破坏机理要复杂很多，而且影响因素也众多，即使在试验条件完全相同的情况下，试件的疲劳寿命也存在着很大的离散性.因此，想要在实际应用中运用材料结构的物理量来定量的分析疲劳寿命具有一定的难度.为了正确反映在不同纤维掺量下疲劳寿命的变化规律，运用概率理论对混凝土疲劳寿命与可靠性进行宏观分析和估计就显示出逻辑上、理论上和实质上的必要性和合理性.许多专家学者进行了相关研究并获得了一定成果.

1　疲劳寿命的两参数威布尔分布概率模型

1939年，瑞典物理学家Weibull提出了威布尔分布，并把它应用到疲劳试验的数据分析中.Leiblein和Zenlen在1956年对滚珠轴承的疲劳试验中也用到了威布尔分布.1956年美籍华人高寿康将威布尔分布用于电子管的寿命试验中.此后，威布尔分布广泛应用于各种零部件和产品的寿命分析，在可靠性分析中占有重要的地位.

威布尔分布密度函数为：

(1)

其中：m为“形状参数”；α为“尺度参数”，又称“特征寿命”；γ为“位置参数”，又称“起始参数”或“最小寿命”.当m= 1时称fw为两参数指数分布密度函数，因此指数分布是威布尔分布的特殊情况.当m=2时，为瑞利分布当m=3～4时，为接近正态频率函数.

γ参数是产品的最小寿命，因此称γ为起始参数但在实际中，γ往往为零，此时

(2)

上式称为两参数威布尔分布密度函数当m=1时，则为单参数的指数分布密度函数.

对式(2)进行积分便可得到威布尔分布函数：

(3)

2　试验概况

2.1试验材料与试件制作

本试验使用的材料是由湖南大学生产的活性粉末混凝土(型号是RPC200)和镀铜光面平直钢纤维(直径0.16±0.005mm，长度12±1mm，抗拉强度>2000MPa).

试件尺寸设计为40mm×40mm×160mm的RPC小梁，有三个钢纤维体积掺量，分别为0%、1%和2%(由于钢纤维体积掺量的增大，搅拌的难度会成倍增加，所以没有配置更高的掺量).根据这三种体积掺量分组分别为S0、S1、S2，每组分别制作11个试件，共33个试件，其中每组中有3个试件将用于静载试验,8个用于抗折疲劳试验.

试件制作完成之后24h脱模，并进行标准养护，28d之后进行静载和疲劳试验.

2.2试验方法

试验分为抗折静载试验和抗折疲劳试验.静载试验是疲劳试验的基础，通过静载试验获得抗折极限强度，然后确定疲劳试验中荷载的上下限值.最大疲劳荷载Pmax是将静载试验中各组试件极限强度的平均值乘以最大应力水平(设置为0.85)，试验中在试件上保持了最小疲劳荷载Pmin以防试件跳脱.根据试验的实际情况，并参考其他文献，选取最小疲劳荷载为Pmin= 1MPa.Pmax和Pmin即为该试验中疲劳荷载的上下限值.

抗折试验设备采用的是浙江中科仪器有限公司生产的SYE—2000型压力试验机，三分点进行加载的方式，即在试件跨径的三分之一点和三分之二点作为加集中荷载的两个点.试验净跨径为L = 120mm，试件高度为h = 40mm，高跨比h/L=1/3.每组试验取用平均值以计算各组的抗折强度.抗折强度计算公式如下：

Ff=FL/bh2

(4)

式中：Ff—RPC试件抗折强度(MPa)；F—RPC试件抗折承载极限能力(N)；L—支座间净跨径长(mm)，L=120mm；b—试件截面宽度(mm)，b=40mm；h—试件截面高度(mm)，h=40mm.

抗折疲劳试验采用MTS810疲劳试验机，3点弯曲试验方式进行循环加载.跨距120mm，高度40mm，跨高比为3.荷载施加于跨中，所施加疲劳荷载波型为正弦波，加载频率为4Hz.

2.3试验结果

抗折试验和抗折疲劳试验数据统计如表1和表2所示.

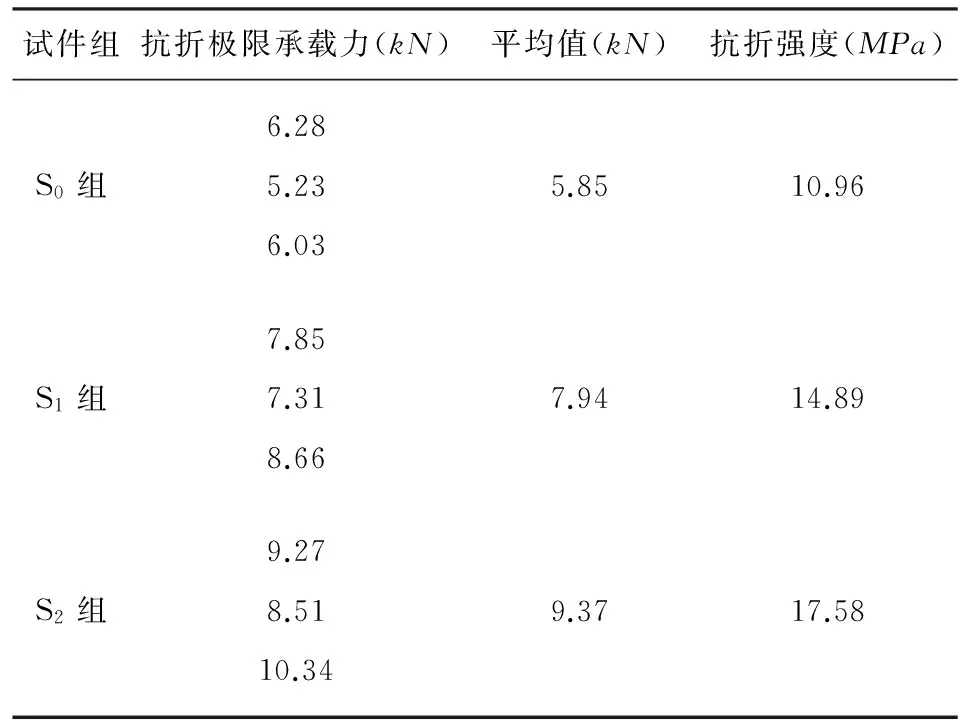
表1　抗折强度试验数据记录及计算

表2　抗折疲劳试验结果统计表

3　各组试件抗折疲劳寿命的威布尔分布检验

在同一应力水平作用下，各试件疲劳寿命N的分布规率可以由以下威布尔密度函数表示：

(N0≤N<∞)

(5)

式中:包含有三个参数：N0—最小寿命参数；Na—特征寿命参数；b—威布尔形状参数(或斜率).

根据威布尔分布的性质以及式(12)，可求出威布尔变量即疲劳寿命N的分布函数F(Np)为：

(6)

F(Np)表示破坏率，则存活率

(7)

Np即表示存活率为P的疲劳寿命.

对上式左右求倒数化简结果如下：

(8)

对上式两边取二次自然对数：

=bln(Np-N0)-bln(Na-N0)

(9)

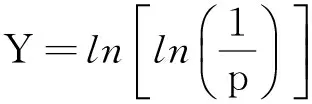
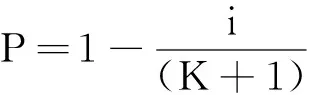
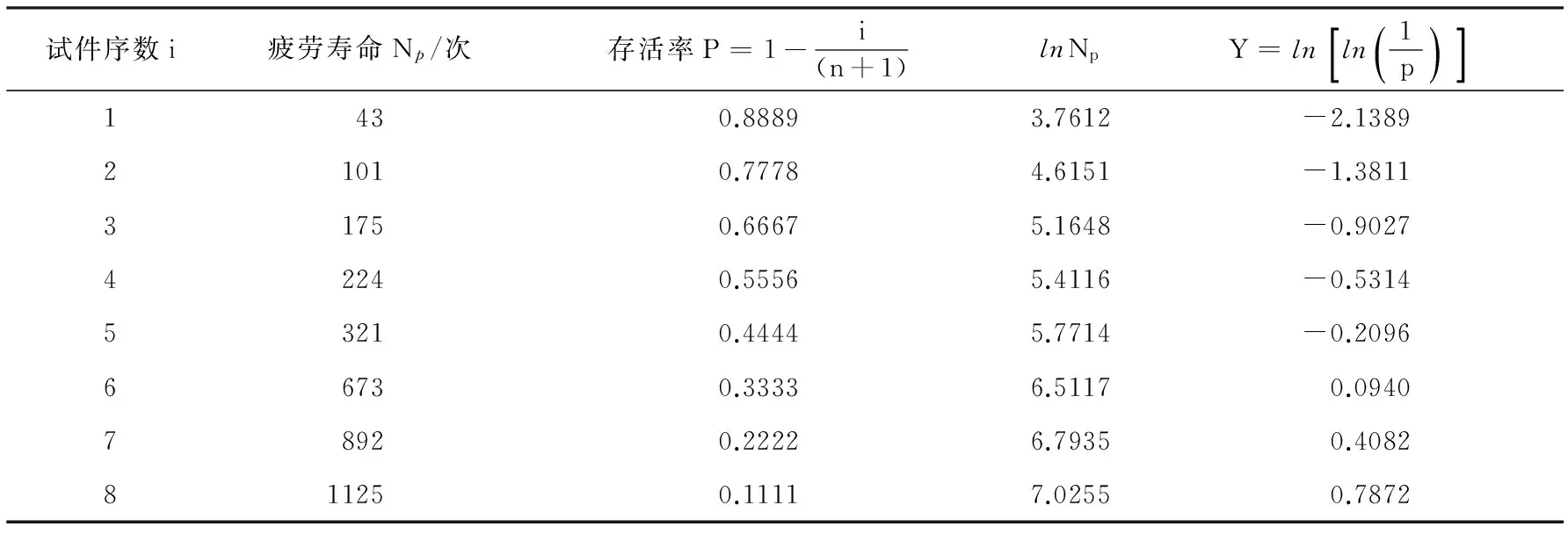
表3　S0试件组抗折疲劳寿命Np的威布尔分布检验

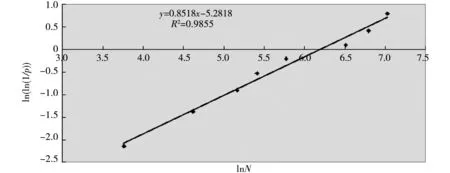
图1　S0试件组抗折疲劳寿命Np的威布尔分布检验表4　S1试件组抗折疲劳寿命Np的威布尔分布检验

试件序数i疲劳寿命Np/次存活率P=1-i(n+1)lnNpY=lnln1p()[]15890.88896.3784-2.1389210270.77786.9344-1.3811332540.66678.0876-0.9027452470.55568.5654-0.5314568970.44448.8388-0.2096675890.33338.93450.0940791240.22229.11870.40828131220.11119.48200.7872

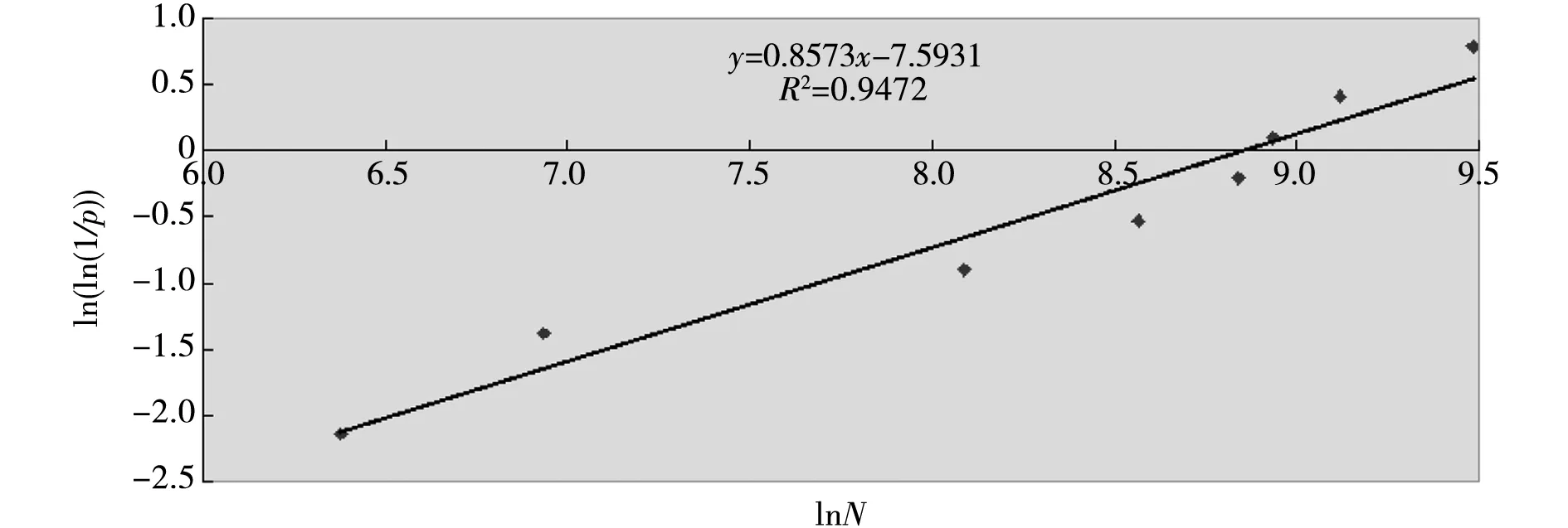
图2　S1试件组抗折疲劳寿命Np的威布尔分布检验表5　S2试件组抗折疲劳寿命Np的威布尔分布检验

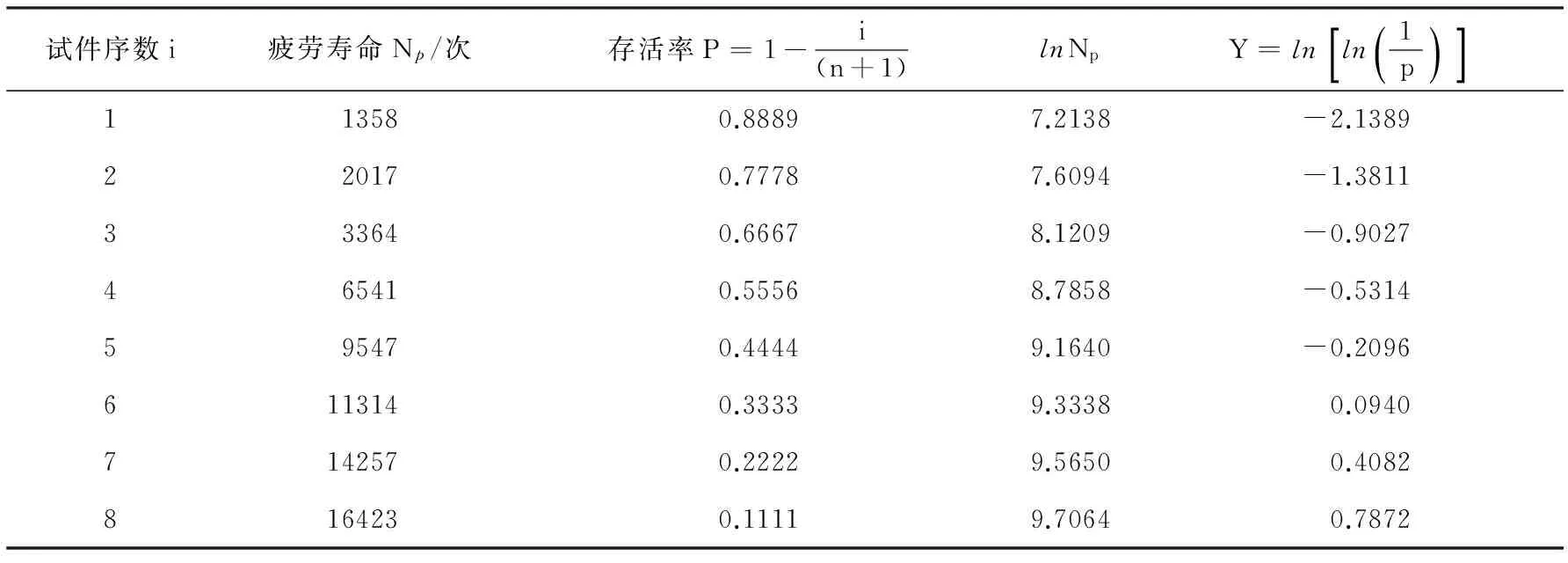
试件序数i疲劳寿命Np/次存活率P=1-i(n+1)lnNpY=lnln1p()[]113580.88897.2138-2.1389220170.77787.6094-1.3811333640.66678.1209-0.9027465410.55568.7858-0.5314595470.44449.1640-0.20966113140.33339.33380.09407142570.22229.56500.40828164230.11119.70640.7872

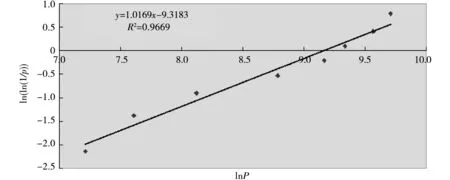
图3　S2试件组抗折疲劳寿命Np的威布尔分布检验

通过图1～图3中的回归分析统计出回归系数、回归方程和相关系数并列表,如表6所示.由此可知，回归分析结果中的相关系数r分别为0.9855、0.9472和0.9669，均在0.9以上，这表明lnNp与Y=ln[ln(1/p)]之间的线性相关关系显著.RPC试件的抗折疲劳寿命很好地服从了两参数威布尔分布.对比表6和表7中可知，威布尔分布的相关系数明显要高于对数正态分布回归，也就是说，RPC的抗折疲劳寿命分布更加符合两参数威布尔分布.

表6　威布尔分布回归分析结果

表7　对数正态分布回归分析结果

注：表格参考文献《活性粉末混凝土抗折疲劳寿命的对数正态分布研究》

4　结　论

(1)钢纤维的掺入有效地增强了RPC的韧性，提高了RPC的疲劳寿命.随着钢纤维的体积掺量的增大，抗折强度增大，抗折疲劳寿命也保持了增长的势头.

(2)从宏观上可以将RPC试件的疲劳损伤演化过程分为三个不同阶段，分别是裂纹潜伏阶段、裂纹稳定扩展阶段和失稳破坏阶段，他们所占疲劳寿命的百分比分别为15%、75%和10%.

(3)RPC试件的抗折疲劳寿命很好地服从了两参数威布尔分布，而且比对数正态分布的拟合程度更高.

[1]杜婷,郭太平,林怀立,刘中心,周志强.混凝土材料的研究现状和发展应用[J].混凝土,2006(5):7-9.

[2]施涛,叶青.活性粉末混凝土的研究和应用中存在的问题[J].建筑石膏与胶凝材料,2003(5):23-25.

[3]石成恩.活性粉末混凝土(RPC)的弯曲疲劳寿命研究[D].福建：福州大学硕士学位论文,2004.

StudyonFlexuralFatigueLifeWeibullContributionofRPC

YANGKe-wen，LUOXu-guo

(SchoolofCivilEngineering,HunanUniversityofScienceandTechnology,Xiangtan411201,China)

ReactivePowderConcrete(RPC)isanewtypeofcompositecement-basedmaterial.Becauseofitsultra-highstrength,hightoughness,highdurabilityandotherexcellentproperties，RPCattractsmoreandmoreattentionandisstudiedbymanyscholars.WiththeresearchdeepeningthestudyontheRPCmaterialwillbewidelyusedinpracticalengineering.ThepaperstudiesthefatiguelifedistributionofRPCbytestingonthethreedifferentcontentsofsteelfibervolumespecimens.Throughthefatiguetestwegettheflexuralfatigueloadingtimesofthespecimens,andverifytheweibulldistributionoffatiguelifeofRPCbyfatiguestatisticaltheory.

reactivepowderconcrete;steelfibre;flexuralfatiguetest;fatiguelife;Weibulldistribution

2015-09-21

湖南科技大学研究生创新基金资助项目(S130011).

杨科文(1990-)，男，硕士研究生，研究方向：桥梁与隧道工程.

TB321

A

1671-119X(2016)01-0076-05