导电板覆盖的开孔矩形腔体电磁屏蔽效能的比较研究

焦重庆　李顺杰

（新能源电力系统国家重点实验室（华北电力大学） 北京　102206）

导电板覆盖的开孔矩形腔体电磁屏蔽效能的比较研究

焦重庆李顺杰

（新能源电力系统国家重点实验室（华北电力大学） 北京102206）

针对导电板覆盖的开孔矩形腔体，比较了SEi、SEa、SEm3种屏蔽效能（SEi为入射场与开孔覆盖导电板时腔体内部某位置的透射场场强大小的比值，SEa为开孔敞开与开孔覆盖导电板时腔体内部同一位置的透射场场强大小的比值，SEm为开孔覆盖参考导电板与开孔覆盖待测导电板时腔体内部同一位置的透射场场强大小的比值）。利用解析理论方法和全波仿真方法计算分析了腔体谐振和观测点位置对3种屏蔽效能的影响规律，两种方法的计算结果一致性良好。结果表明，SEi受这两个因素的影响很明显，SEa受到的影响相对较小，而SEm几乎没有受到影响，且SEm与一个无限大板相对于另一个无限大板的屏蔽效能近似相等，这一特性使其在材料电磁屏蔽效能的评估中有着潜在的应用价值。

电磁屏蔽屏蔽效能屏蔽腔体开孔导电材料

0　引言

电磁屏蔽是抑制由空间场耦合机制产生的电磁干扰的主要技术措施之一。实际应用中，通常用金属箱体将潜在的骚扰源或敏感设备包围起来，在某种程度上可以减弱透射场或泄漏场，起到电磁屏蔽的效果［1-3］。

然而，实际上屏蔽腔体必然会存在一些孔，导致腔体的屏蔽效能（Shielding Effectiveness，SE）急剧下降。在某些对屏蔽要求较严格的部位，需要在孔上覆盖导电材料或吸波材料（如金属网，垫片及各式各样的复合材料），以确保透射场或泄漏场在允许的范围内［4-8］。随着材料科学与技术的快速发展，越来越多质量轻、柔韧性好的导电材料应用于电磁屏蔽领域［9-14］。因此对导电材料屏蔽效能的评估具有实际意义。

目前，导电材料屏蔽效能测试中采用的屏蔽室法的模型为电磁波照射下的开孔矩形腔体，利用开孔有无覆盖屏蔽材料时腔体内某观测点的透射场场强大小之比评估材料的SE。然而，大量研究表明，这样定义的SE会受空腔谐振、观测点位置、腔体尺寸及开孔尺寸的影响［15-20］，有些情况下在谐振频率处的屏蔽效能会出现负值，但不能由此认为材料的屏蔽效能为负，因此这样定义的SE不能很好地评价材料的屏蔽效能。文献［17］研究了矩形腔体整个面覆盖导电材料时的情况，该模型过于简化，本文研究的是矩形腔体某个面上的开孔覆盖导电材料时的情况，与屏蔽室法的模型相符。

为减弱谐振效应、位置效应和尺寸效应的影响，本文提出了新定义的SE，并进行了讨论分析。从数值结果上表明，这种SE可以几乎不受尺寸效应、谐振效应和位置效应的影响，特别是它等同于无限大待测板与无限大参考板对垂直入射平面波的相对屏蔽效能，因此它反映了材料本身的电磁特性，去除了测试过程中屏蔽箱对所测的屏蔽效能的影响，为材料屏蔽效能评估方法提供了新思路。

1　模型与计算方法

本文的研究模型为入射平面波照射下的开孔矩形腔体，坐标系如图1a所示，坐标原点位于矩形腔体右下角的顶点，矩形腔体在x、y、z方向上的长度分别为a、b、d。腔体的厚度忽略不计，材料为理想导体，在其前壁（z=0）中心处开孔，孔的长度和宽度分别为L和W。孔被厚度为t、电导率为σ的导电板覆盖。入射平面波的传播方向为z、极化方向为y。

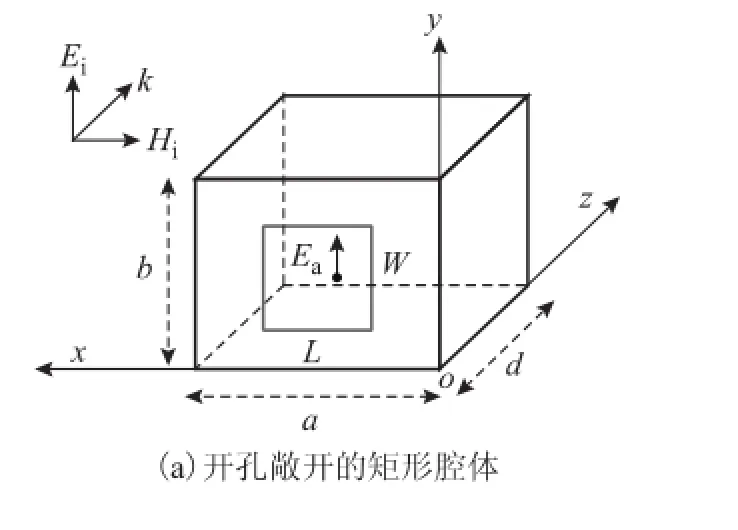
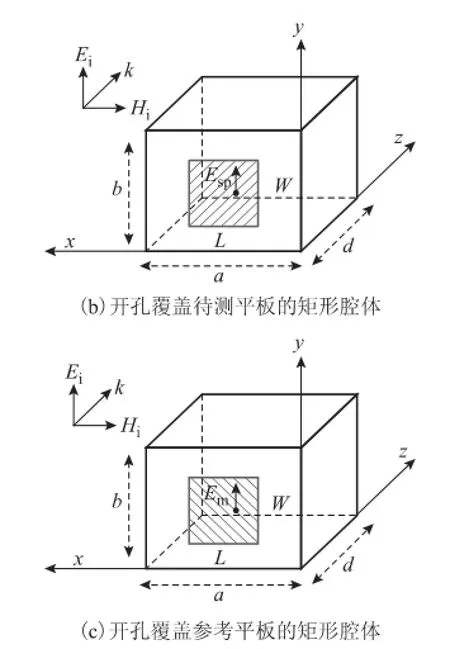
图1　入射平面波照射下的开孔矩形腔体Fig.1　A rectangular shielding box with a rectangular aperture under the illumination of an incident plane wave

传统的SE（SEi）和两种新的SE（SEa和SEm）分别定义为

式中，Ei为入射平面波的电场强度；Ea为开孔敞开（未覆盖导电板）时腔体内部透射场电场强度；Esp为开孔覆盖待测平板时腔体内部透射场的电场强度；Em为开孔覆盖电导率为σ0的参考板时腔体内部透射场电场强度。

如图1所示，所有电场强度的观测点都位于同一位置且只考虑y方向的电场分量。由式（1）～式（3）可知，3种屏蔽效能均为比值形式，且它们的分母相同、分子不同，所反映的SE的物理含义也有所不同，其中SEi反映的是覆盖导电板的开孔腔体的综合屏蔽效能；SEa反映的是开孔覆盖导电板的腔体与开孔敞开的腔体的相对屏蔽效能；SEm反映的是开孔覆盖待测板的腔体与开孔覆盖参考板的腔体的相对屏蔽效能。

本文中，Ea的计算是基于文献［21］给出的模式展开-矩量法混合方法，Esp的计算是基于文献［22］给出的中间级电路模型方法。由于这两种方法均为半解析方法，因此计算速度快。同时，本文给出全波仿真软件CST-MWS的频域求解器计算结果与上述两种方法计算结果进行对比。

2　结果与讨论

选取屏蔽腔体尺寸a=b=d=30 cm，开孔尺寸L=W=5 cm，导电板厚度t=1 mm，导电板为非磁性材料，其介电常数和磁导率与真空相同。图2为导电板σ分别为100 S/m和1 000 S/m时，SEi随入射平面波频率的变化曲线，其观测点为P（15 cm，15 cm，15 cm）。由图2可看出谐振效应对SEi的影响显著。极小值出现在f=0.7 GHz附近，其原因是腔体的谐振效应，一个腔体有一系列的谐振模式，对应的TEmnp模式谐振频率为

式中，fmnp为谐振频率，MHz；a、b、d为屏蔽腔体的尺寸，m；m、n、p为自然数，一次只能一个为零，分别对应腔体内部某个传播模式。本文中屏蔽腔体的尺寸为30 cm×30 cm×30 cm，由式（4）计算其最低谐振频率约为707 MHz，对应于TE101模式，当入射波的频率与腔体内部某传播模式的谐振频率接近时，该模式的振幅会急剧增大，导致腔体内部的场急剧增大，SEi急剧减小。

图2　不同电导率下SEi随频率的变化曲线，其观测点为P（15 cm，15 cm，15 cm）Fig.2　Dependence of SEion the wave frequency with field point P（15 cm，15 cm，15 cm）for different values of the conductivity

在f=1.04 GHz附近出现极大值，其原因为将屏蔽腔体看成沿z方向放置的矩形波导，波导在z=d处短路，电磁场发生全反射，形成驻波场，沿z方向电场幅值分布近似为

式中，d为屏蔽腔体在z方向的长度，m；z为观测点z方向坐标位置，m；kz为相位常数，rad/m。观测点位置位于腔体中心，即z=d/2。由驻波节点处E=0即sinkz（d-z）=0，计算得到当频率f≈1.1 GHz时，z= d/2处为TE10波导模式形成的驻波节点。上述现象也可理解成TE102腔体模式在1.1 GHz处谐振，且该模式在腔体中心点处有场分布的节点（零点）。图2中曲线的极大值约在1.04 GHz附近，频率不完全一致的原因在于开孔的存在对谐振频率有向下的扰动。

图3为导电板σ=100 S/m，入射平面波f分别为0.3 GHz和1 GHz时，SEi随观测点P（15 cm，15 cm，z）z坐标轴的变化曲线。由图3可知，当观测点P沿线段x=15 cm，y=15 cm，0＜z＜30 cm移动时，SEi受观测点位置的影响也很严重，原因在于驻波场的分布特点，当f=0.3 GHz时，kz≈j8.38 rad/m是一个虚数，此时电场E是关于z的减函数，SEi随z的增加而增大，如图3中f=0.3 GHz曲线所示。当f=1 GHz时，kz≈18.14 rad/m，则TE10模式在z方向上的驻波节点位于z=d-π/kz≈130 mm处，所以图3中f= 1 GHz曲线在z=130 mm附近出现极大值。因此，当用SEi描述屏蔽腔体SE特性的同时要注意考虑其空间的分布特点。由图2和图3可看出，解析的理论方法与全部仿真方法的计算结果有很好的一致性。图4为导电板σ=1 000 S/m，开孔尺寸L=W=3 cm、6 cm和9 cm时，SEi随入射平面波频率的变化曲线，其观测点为P（15 cm，15 cm，15 cm）。由图4可知，SEi受开孔尺寸的影响，SEi随开孔尺寸的增大而减小，这是由于开孔尺寸增大，用于覆盖开孔的导电板的面积就会增大，导致腔体内部透射场增大，SEi减小。综上所述，SEi受到谐振效应、位置效应和开孔尺寸的影响较大，描述的是屏蔽腔体和导电板整体的屏蔽效能，不能用它描述材料本身的电磁屏蔽性能。

图3　导电板σ=100 S/m时，不同频率下SEi随观测点P（15 cm，15 cm，z）的变化曲线Fig.3　Dependence of SEion the field point P（15 cm，15 cm，z）with σ=100 S/m for different values of the wave frequency

图4　导电板σ=1 000 S/m时，不同开孔尺寸下SEi随频率的变化曲线，其观测点为P（15 cm，15 cm，15 cm）Fig.4　Dependence of SEion the wave frequency with field point P（15 cm，15 cm，15 cm）and σ=1 000 S/m for different size of the aperture

图5为导电板σ=100 S/m和1 000 S/m时，SEa随入射平面波频率的变化曲线，其观测点为P（15 cm，15 cm，15 cm）。图6为导电板σ=100 S/m，入射平面波f分别为0.3 GHz和1 GHz时，SEa随观测点P（15 cm，15 cm，z）z坐标轴的变化曲线。从图5中可发现，与图2相比谐振效应有所减弱，谐振效应只影响f=0.7 GHz附近较窄的一段频带宽度。同时，驻波的分布特性影响的频率范围（f=1.04 GHz附近）也明显减小。并且，图6所示位置效应也显著减弱，其原因在于Ea和Esp具有相似的空间结构，因为这种结构主要是由腔体的尺寸结构决定。对于Ea，腔体的孔是敞开的，由于开孔的尺寸相对于整个腔体来说很小，所以Ea的空间结构与全封闭腔体的空间结构相比不会有本质的改变。从图5和图6中可以看出，解析的理论方法与全波仿真方法的计算结果也具有很好的一致性。但频率低于100 MHz（图中没有画出）时，这种一致性会变差。原因在于文献［4］中的模型采用转移阻抗来描述板层的电磁透射特性，这种方法要求板对照射来的电磁波有足够的衰减能力。通过增加电磁波的频率或增加板的电导率才能达到足够的衰减能力。图7为导电板σ=1 000 S/m，开孔尺寸L=W=3 cm、6 cm和9 cm时，SEm随入射平面波频率的变化曲线，其观测点为P（15 cm，15 cm，15 cm）。由图7可知，SEa随开孔尺寸的增大而增大。SEa虽然受谐振效应和位置效应的影响较小，但受开孔尺寸的影响较大，它描述的是材料用于密封时对整体屏蔽效能的改善情况，用其来描述材料本身的电磁屏蔽性能是不恰当的。

图5　不同电导率下SEa随频率的变化曲线，其观测点为P（15 cm，15 cm，15 cm）Fig.5　Dependence of SEaon the wave frequency with field point P（15 cm，15 cm，15 cm）for different values of the conductivity

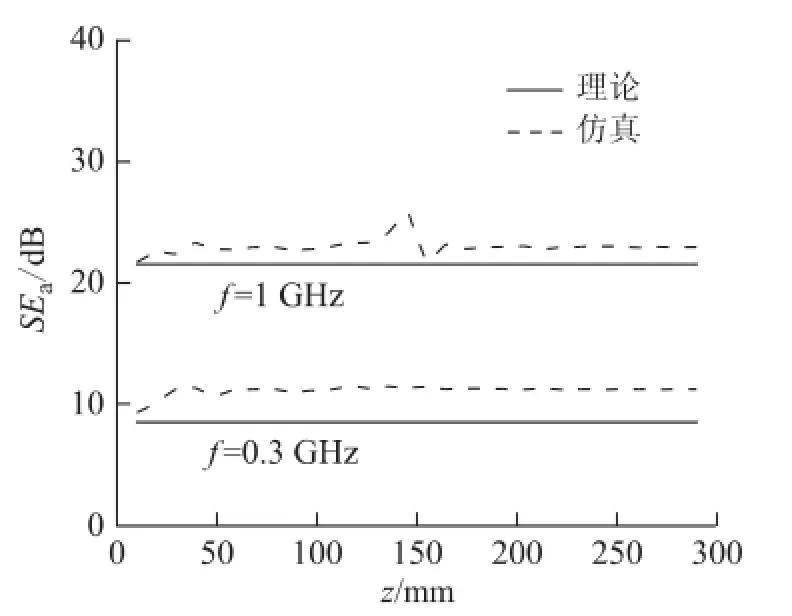
图6　导电板σ=100 S/m时，不同频率下SEa随观测点P（15 cm，15 cm，z）的变化曲线Fig.6　Dependence of SEaon the field point P（15 cm，15 cm，z）with σ=100 S/m for different values of the wave frequency

图7　导电板σ=1 000 S/m时，不同开孔尺寸下SEa随频率变化曲线，其观测点为P（15 cm，15 cm，15 cm）Fig.7　Dependence of SEaon the wave frequency with field point P（15 cm，15 cm，15 cm）and σ=1 000 S/m for different size of the aperture

假设参考板的电导率σ0=100 S/m，图8为导电板σ=300 S/m、500 S/m和1 000 S/m时，SEm随频率的变化曲线。图9为入射平面波f=1 GHz，导电板σ=300 S/m，500 S/m和1 000 S/m时，SEm随观测点P（15 cm，15 cm，z）z坐标轴的变化曲线。图10为导电板σ=1 000 S/m，开孔尺寸L=W=3 cm、6 cm和9 cm时，SEm随入射平面波频率的变化曲线。由图8～图10可看出，SEm不受谐振效应、位置效应和开孔尺寸的影响。从物理意义上看，SEm中的分子和分母唯一的差别是覆盖的材料的区别，因此它不受腔体的影响，主要是两种材料的区别。同时，SEm便于得出不同材料的屏蔽效能的优劣和层次序列，若其值为正，说明待测材料的屏蔽效能优于参考材料的屏蔽效能；若其值为负，说明待测材料的屏蔽效能差于参考材料的屏蔽效能。

图8　不同电导率下SEm随频率的变化曲线，其观测点为P（15 cm，15 cm，15 cm）Fig.8　Dependence of SEmon the wave frequency with field point P（15 cm，15 cm，15 cm）for different values of the conductivity

图9　入射波f=1 GHz时，不同电导率下SEm随观测点P（15 cm，15 cm，z）的变化曲线Fig.9　Dependence of SEmon the field point P（15 cm，15 cm，z）with f=1 GHz for different values of the conductivity

图10　导电板σ=1 000 S/m时，不同开孔尺寸下SEm随频率变化曲线，其观测点为P（15 cm，15 cm，15 cm）Fig.10　Dependence of SEmon the wave frequency with field point P（15 cm，15 cm，15 cm）and σ=1 000 S/m for different size of the aperture

无限大导电板对垂直入射的平面波的SE表达为［1，2］

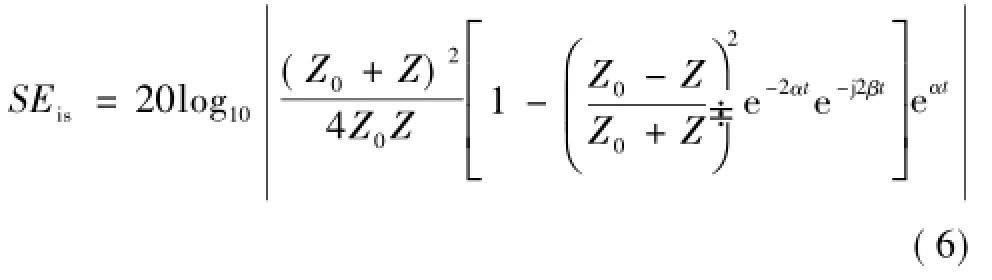
式中，Z0为真空中的波阻抗，Ω；Z为导电板的波阻抗，Ω；α为导电板的衰减常数，Np/m；β为导电板板的相位常数，rad/m。

引入一种新的相对屏蔽效能SEs，定义为电导率为σ的待测板的SE与电导率为σ0的参考板的SE之差。其中待测板和参考板的SE由式（6）计算得到。图11为σ0=100 S/m，σ=300 S/m、500 S/m和1 000 S/m时的SEs与SEm的对比图，其中SEm的值为全波仿真结果。可以看出，当入射波的频率大到一定程度后，SEs与SEm有很好的一致性。由此可以发现，SEm与无限大待测板和无限大参考板对垂直入射平面波的相对屏蔽效能近似相等，因此可知SEm不受屏蔽腔体的影响，它描述的是材料本身的电磁屏蔽性能。

图11　相对屏蔽效能SEm和SEs的对比Fig.11　A Comparison between the relative shielding effectiveness，SEmand SEs

对于待测的电导率未知的材料，其SEm等同于无限大待测板与无限大参考板对垂直入射平面波的相对屏蔽效能，利用该结论可得到:①材料对垂直平面波的屏蔽效能；②以屏蔽效能为基准的材料的等效电导率。选择电导率已知的材料（如石墨板、铝板、铜板等）作为参考板。首先测试待测材料的SEm，参考材料对垂直入射平面波的屏蔽效能由式（6）计算得到。然后，由SEm=SEs可得到待测材料对垂直入射平面波的屏蔽效能，通过式（6）可反演其等效电导率。需要特别指出的是，该电导率通常与频率有关，尤其是对复合材料。

3　结论

针对导电板覆盖的开孔矩形腔体模型，本文比较了SEi、SEa、SEm3种屏蔽效能。利用解析理论方法和全波仿真方法进行屏蔽效能的计算，计算结果表明两种方法的一致性良好。可得出以下结论:

1）以入射场作为参考场的屏蔽效能反映了屏蔽腔体和导电板的综合效应，它对腔体谐振、观测点位置和开孔尺寸非常敏感。

2）以开孔敞开时的透射场作为参考场的屏蔽效能反映了导电板的电磁密封性能，它受腔体谐振和观测点位置的影响较小，但受开孔尺寸的影响较大。

3）以开孔覆盖有参考板时的透射场作为参考场的屏蔽效能反映了待测板对参考板的相对效应。这种屏蔽效能不受腔体谐振、观测点位置、开孔尺寸和腔体尺寸的影响，反映的是材料本身的电磁特性。特别是它等同于无限大待测板与无限大参考板对垂直入射平面波的相对屏蔽效能，利用该结论就可得到待测材料对垂直入射平面波的屏蔽效能，并反演其等效电导率。

［1］CelozziS，AraneoR，LovatG.Electromagnetic Shielding［M］.Hoboken，New Jersey:John Wiley& Sons Inc.，2008.

［2］Paul C R.Introduction to Electromagnetic Compatibility［M］.Hoboken，New Jersey:John Wiley&Sons Inc.，2006.

［3］张向明，赵治华，郭飞，等.电磁兼容测试系统电磁干扰问题分析与解决［J］.电工技术学报，2010，25（10）:14-17，36. Zhang Xiangming，ZhaoZhihua，GuoFei，etal. Electromagnetic interference analysis and its suppression ofEMCtestingsystem［J］.TransactionsofChina Electrotechnical Society，2010，25（10）:14-17，36.

［4］聂一雄，刘艺，王星华.电子式互感器工作电源解决方案研究［J］.电力系统保护与控制，2010，38（14）:39-42. Nie Yixiong，Liu Yi，Wang Xinghua.Research on solution of electronic transducer power supply［J］.Power System Protection and Control，2010，38（14）:39-42.

［5］牟涛，周丽娟，周水斌.高精度电子式电流互感器采集器的设计［J］.电力系统保护与控制，2010，39（20）:141-144. Mu Tao，Zhou Lijuan，Zhou Shuibin.Design of high precison electronic current transformer［J］.Power System Protection and Control，2010，39（20）:141-144.

［6］马海杰，罗广孝，徐刚，等.特高压变电站二次设备电磁兼容建模［J］.电力系统保护与控制，2010，38（7）:53-57. Ma Haijie，Luo Guangxiao，Xu Gang，et al.EMC model of secondary equipment in UHV substation［J］. Power System Protection and Control，2010，38（7）: 53-57.

［7］焦重庆，牛帅，李琳.复合材料工频电场和工频磁场屏蔽效能实验研究［J］.电工技术学报，2015，30（10）:1-6. Jiao Chongqing，Niu Shuai，Li Lin.Experiment study of powerfrequencyelectricandmagneticshieding effectiveness for composite materials［J］.Transactions of China Electrotechnical Society，2015，30（10）:1-6.

［8］JiaoCQ.Shieldingeffectivenessimprovementof metallic waveguide tube by using wall losses［J］.IEEE Transactions on Electromagnetic Compatibility，2012，54（3）:696-699.

［9］Bogorad A L，Deeter M P，August K A，et al. Shielding effectiveness and closeout methods for composite spacecraft structural panels［J］.IEEE Transactions on Electromagnetic Compatibility，2008，50（3）:547-555.

［10］Kuzhir P P，Paddubskaya A G，Maksimenko S A，et al.Carbon onion composites for EMC applications［J］. IEEE Transactions on Electromagnetic Compatibility，2012，54（1）:6-16.

［11］Sarto M S，D’Aloia A G，Tamburrano A，et al. Synthesis，modeling，and experimental characterization ofgraphitenanoplatelet-basedcompositeforEMC applications［J］.IEEE Transactions on Electromagnetic Compatibility，2012，54（1）:17-27.

［12］曲兆明，雷忆三，王庆国，等.高效电磁屏蔽复合材料设计及其屏蔽效能测试［J］.高电压技术，2012，38（9）:2343-2348. Qu Zhaoming，LeiYisan，WangQingguo，etal. Designofhighefficiencyelectromagneticshielding composites and its shielding effectiveness test［J］.High Voltage Engineering，2012，38（9）:2343-2348.

［13］Gifuni A.Relation between the shielding effectiveness of an electrically large enclosure and the wall material under uniformandisotropicfieldconditions［J］.IEEE Transactions on Electromagnetic Compatibility，2013，55（6）:1354-1357.

［14］Andrieu G，Panh J，Reineix A，et al.Homogenization of composite panels from a near-field magnetic shielding effectiveness measurement［J］.IEEE Transactions on Electromagnetic Compatibility，2012，54（3）:700-703.

［15］陈翔，陈永光，魏明，等.基于屏蔽暗箱窗口法的材料电磁脉冲屏蔽效能的时域测试［J］.高电压技术，2013，39（3）:668-674. ChenXiang，ChenYongguang，WeiMing，etal. Time-domain test for electromagnrtic pulse shielding effectiveness of matnrials based on the method of windowed semianechoicBox［J］.HighVoltageEngineering，2013，39（3）:668-674.

［16］Jiao CQ，ZhuHZ.Resonancesuppressionand electromagnetic shielding effectiveness improvement of an apertured rectangular cavity by using wall losses［J］. Chinese Physics B，2013，22（8）:404-409.

［17］牛帅，焦重庆，李琳.中等导电性材料覆盖的金属腔体的电磁屏蔽效能研究［J］.物理学报，2013，62（21）:214102-214107. Niu Shuai，Jiao Chongqing，Lilin.Shielding effectiveness of a metal cavity covered by a material with a medium conductivity［J］.ActaPhysicaScience，2013，62（21）:214102-214107.

［18］ 范杰清，郝建红，柒培华.基于扩展传输线法的异型腔电场屏蔽效能［J］.电工技术学报，2014，29（5）:228-232，238. Fan Jieqing，Hao Jianhong，Qi Peihua.Electric field shielding effectiveness of heterotypic enclosures based on adjusted transmission line method［J］.Transactions of China ElectrotechnicalSociety，2014，29（5）:228-232，238.

［19］ Wang Q G，Cheng E W，Qu Z M.On the shielding effectiveness of small dimensionenclosuresusinga reverberationchamber［J］.IEEETransactionson Electromagnetic Compatibility，2011，53（3）:562-569.

［20］Marvin A C，Dawson L，Flintoft I D，et al.A method for the measurement of shielding effectiveness of planar samples requiring no sample edge preparation or contact［J］.IEEE Transactions on Electromagnetic Compatibility，2009，51（2）:255-262.

［21］DehkhodaP， TavakoliA， MoiniR.Shielding effectiveness of a rectangular enclosure with finite wall thickness and rectangular apertures by the generalized modal method of moments［J］.IET Science Measurement Technology，2009，3（2）:123-136.

［22］Konefal T，Dawson J F，Marvin A C，et al.A fast circuit model description of the shielding effectiveness of a box with imperfect gaskets or apertures covered by thin resistivesheetcoatings［J］.IEEETransactions Electromagnetic Compatibility，2006，48（1）:134-144.

Shielding Effectiveness Comparison of a Rectangular Box with an Aperture Covered by Conductive Sheet

Jiao ChongqingLi Shunjie
（State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources North China Electric Power UniversityBeijing102206China）

Three different definitions of shielding effectiveness for a shielding box with an aperture covered by conductive sheet are considered:i.e.the shielding effectiveness SEiwith the incident field taken as reference field，SEawith the penetration field in case of the aperture opened as reference field，and SEmwith its reference field defined as the penetration field when a reference sheet employed.Effects of the two factors，cavity resonance and observation point position，are investigated numerically for the three different types of shielding effectiveness.It is shown that SEiis affected strongly by the two factors，SEais affected comparatively lessand SEmishardly influenced.Especially，SEmcan be explained as the shielding effective of an infinite conductive sheet relative to the other one.This feature makes it very useful for shielding effectiveness evaluation of conductive material.

Electromagnetic shielding，shielding effectiveness，shielding box，aperture，conductive material

TM15

国家自然科学基金项目（51307055）和国家电网公司项目（SGRI-WD-71-12-009）资助。

2015-06-25改稿日期 2015-07-29

焦重庆男，1981年生，博士，副教授，研究方向为电磁场理论及其应用和电力系统电磁兼容。

E-mail:cqjiao@ncepu.edu.cn（通信作者）

李顺杰男，1991年生，硕士研究生，研究方向为电力系统电磁兼容。

E-mail:lianganglsj@163.com