一种减小四象限级联型变换器母线电容纹波电压的控制方法

张宏亮　周　鹏

（郑州航空工业管理学院，郑州 450046）

一种减小四象限级联型变换器母线电容纹波电压的控制方法

张宏亮周鹏

（郑州航空工业管理学院，郑州 450046）

在交流电动机调速领域，传统级联型多电平变换器的应用越来越广泛，但是由于无法实现能量回馈，因而应用场合受到限制。通过采用有源PWM整流模块取代不控整流模块可以实现能量回馈，但是由于PWM整流模块输入侧需要滤波电感，导致系统体积和成本增加，限制这种实现方式的实际应用。传统级联型变换器模块的逆变侧采用的是H桥拓扑，导致母线电容纹波电压非常大，需要较大的母线电容，增加了模块的体积和成本。本文提出一种采用输入变压器的付边漏感取代滤波电感的方式，同时提出了一种新颖的控制方式，通过对PWM整流模块控制实现减小母线电容纹波电压，这就样可以减小母线电容，进而降低系统成本，虽然会导致模块PWM整流模块输入电流变差，但是由于存在三相谐波相抵消特性以及通过PWM整流模块的载波移相处理，变压器原边输入电流谐波非常低。理论分析和仿真证明，这种控制方式是可行的。

级联型多电平变换器；四象限；PWM整流器；载波移相

在中压大功率变频调速领域，传统的级联型多电平变换器［1-2］由于具备输出电压等级高、输出电流谐波低以及多电平输出等优点，在风机泵类等中压大功率调速场合取得到了非常广泛的应用［3-4］。但是由于传统级联型变换器的模块采用二极管不控整流输入方式，无法实现能量回馈，因此有文献提出能量回馈型四象限级联型变换器［5-6］。如图3所示，这种变换器采用有源PWM整流输入方式，可以实现能量的回馈。由于PWM整流器输入需要输入滤波电感，必然导致系统需要更大的空间和成本，因此其实际应用受限。级联型变换器模块的逆变侧都采用H桥输出，导致母线电容纹波电压非常大，因此通常传统级联型变换器模块的母线电容非常大，这样就导致电容的成本占据了整个模块的成本大部分。当采用有源PWM整流输入时，可以通过控制来减小母线电容的纹波电压。本文提出了采用输入变压器漏感取代滤波电感的方式，同时提出了一种新颖的控制方式，可以减小母线电容纹波电压进而可以减小母线电容，虽然会导致PWM整流器输入电流变差，但是由于存在三相谐波抵消特性，不会影响变压器原边的输入电流，通过对PWM整流器的载波移相处理后，进一步降低了变压器原边输入电流的谐波。理论分析和仿真结果表明这种控制方案是可行的。

1　传统级联型逆变器

传统级联型逆变器拓扑结构如图1所示，模块的拓扑结构如图2所示，每一相都由一定数量的模块串联构成，实际串联个数由变换器输出电压等级决定。输入采用二极管不空整流器，模块输入电流的THDi非常大，所以输入要加移相变压器，实现模块输入电流谐波相抵消，在变压器原边输入电流更加接近正弦。

图1　级联型多电平变换器拓扑结构

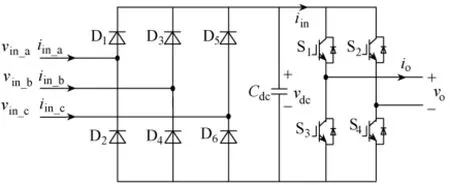
图2　传统级联型逆变器模块拓扑结构

为了实现整个逆变器的多电平电压输出，将载波移相SPWM技术引入到级联型变换器中，即将每个H桥逆变器的载波错开一定角度，以叠加出多电平电压波形。每个模块载波的最佳移相角为

式中，逆N为逆变器每相的模块数量，在这种控制方法下，逆变器输出线电压电平数为：

整个逆变器输出电压的等效载波频率为N倍的模块载波频率，可以有效降低输出电压、电流谐波，而幅值并不损失［7-8］。

这种拓扑结构的模块由于采用二极管整流输入，能量只能单方向流动不具备能量回馈的能力，这样就导致应用场合受限，不能应用到需要能量回馈的场合，如矿井提升和传送带领域。另外由于模块采用单相H桥逆变输出，必然导致母线上有较大的纹波，下面先从理论上分析母线电容较大纹波产生的原因。

如果忽略模块输出电压和电流的谐波，只考虑基波分量，那么模块输出的电压和电流如式（3）所示：

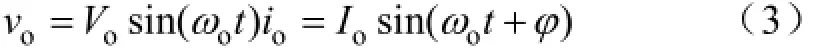
可计算出每一每模块输出的瞬时功率为

如果不考虑模块的损耗，那么模块直流侧输入和逆变侧输出的瞬时功率守恒，pin=vdciin，由pin=po可以得到

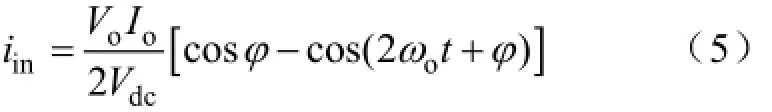
式（5）表明逆变器直流侧输入电流iin包含一个直流分量和一个二倍频纹波（逆变器输出频率的二倍），这个二倍频纹波通常是低频纹波，特别是当变频器在低频工作时，可以低至几十赫兹，要靠母线电容来吸收这个低频的纹波电流。由于频率较低，要吸收这么低频率的纹波电流，通常要加很大的直流母线电容，而电容是电力电子变换器中比较脆弱的元器件，如果纹波过大，会造成电容的寿命大大降低。另外过大的电容也会造成系统成本的大幅增加，因此如果能减小这个二倍频纹波，不但可以提高电容的寿命，而且可以大幅降低成本。但是由于二极管不空整流器是不可控的，所以不能通过控制来减小母线电容的二倍频纹波，要想控制这个二倍频纹波，必须采用可控的输入源。

2　可以消除二倍频纹波和四象限运行的功率模块

前面提到的二极管整流模块结构的缺点是不但不能实现能量回馈，而且母线电容存在较大的二倍频纹波。另外由于二极管整流器不可控，所以也不能通过控制实现二倍频纹波的消除。因此有文献从能量回馈的角度提出采用PWM整流器替换二极管整流器，这样就可以实现电机的能量回馈，即可以实现四象限运行，同时输入整理变压器可以不采用移相变压器，降低了变压器制造的复杂度。但是这样也存在问题，就是PWM整流器输入滤波电感的问题。中压变频器输出功率非常大，通常是MW级的，这样就要求每个模块的输出功率也非常大，PWM整流器的功率器件通常只能选择大功率IGBT。由于损耗和温升限制，IGBT的开关频率很低，通常在几kHz左右，这样就要求输入滤波电感不能太小，否则不能正常工作。如果外加电感，必然会占据大量的空间，级联型变换器由于前级必须有输入变压器，体积已经非常庞大，如果再加入滤波电感的空间，必然导致体积的进一步增加，同时成本也会大幅提升。因此可以采用整流变压器付边输出漏感的方式取代外加电感，变压器漏感通常不大，在不高的开关频率条件下，这会造成PWM整流器电流纹波较大，进而会影响变压器原边输入电流。可以对PWM整流器SPWM控制的载波进行移相，移相角为360°/k，k为模块数量。这样可以抵消一部分开关频率级的纹波，减小变压器输入侧电流谐波。

仿真分析表明，这样是可行的。前级输入改为PWM整流器，就可以通过对PWM整流的控制来减小母线电容的二倍频纹波，首先理论分析这样做的可行性。

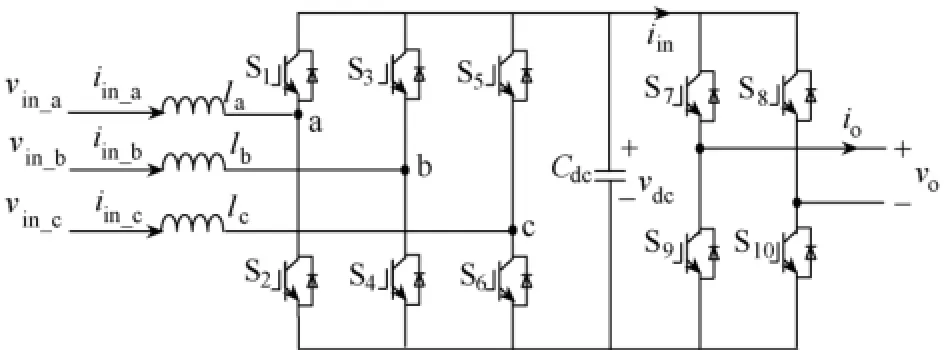
图3 PWM整流输入模块拓扑结构

图3是采用PWM整流器输入模块的拓结构，Vin_a、Vin_b和Vin_c是整流变压器付边输出电压，其频率和幅值一样，只是彼此相位差为2π/3，以Vin_a为例：

PWM整流器可以单位功率因数运行，iin_a、iin_b和iin_c是PWM整流模块输入电流，其频率和幅值也一样，只是彼此相位差为2π/3，以iin_a为例：

可求得模块的瞬时输入功率为

实际系统不存在零序分量，根据瞬时功率理论，dq瞬时输入功率为

如果将模块的单相输出看做为一个三相不平衡的系统，那么αβ0坐标系的瞬时功率为

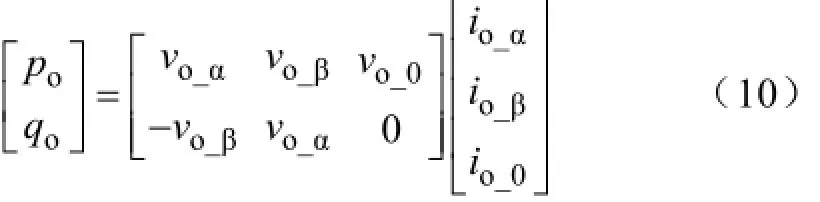
输入瞬时功率平衡pin=po，qin=qo。可以计算出期望的电流值为

通常电网是平衡的，Vin_d是个恒定的常量，Vin_d=0，如果控制系统的无功功率，期望的电流参考值为

若果不考虑变频器的损耗，可以iA1_a为例计算出模块A1的三相输入电流为

从式（13）可以看出，模块A1的输入电流中包含和输入电压同相位分量，同时还包含ωin+2ωo和ωin-2ωo分量，A1模块的b相和c相输入电流和a相一样，只是相位相差2π/3。

模块B1和模块C1的a相输入电流分别为

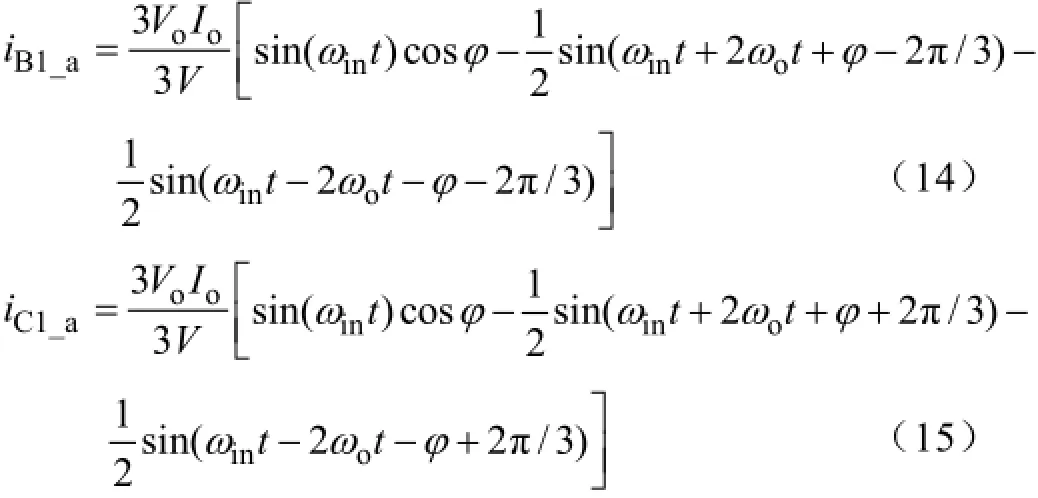
由式（14）和式（15）可以发现，输出A、B和C三相的A1、B1和C1模块各自a相电流的ωin+2ωo和ωin-2ωo分量可以在变压器付边相互抵消，如式（16）所示：

这些分量在变压器付边相互抵消，不会影响变压器的原边电流。同理可知A1、B1和C1模块b相和c相电流也一样。

3　PWM整流器的控制

PWM整流模块输入电流的控制性能是整个系统控制的一个关键。从本质上讲，整流器是关于电能交直流转换的能量变换系统。因为电网电压是基本上一定的，所以对输入电流快速有效的控制也就有效地控制了能量流动方向、速度和大小。有源整流模块输入电流满足下式［9］：

式（17）和式（18）中urd=Sdudc，urq=Squdc，Sd和Sq是dq变换后开关函数。d、q轴电流除受控制量urd、urq的影响外，还受耦合电压ωLiq、ωLid扰动和电网电压usd、usq扰动。所以单纯的对d、q轴电流作负反馈并没有解除d、q轴之间的电流耦合，效果不是很理想。

现假设变换器输出的电压矢量中包含3个分量，即Urd包含urd1、urd2、urd3，Urq包含urq1、urq2、urq3，可得

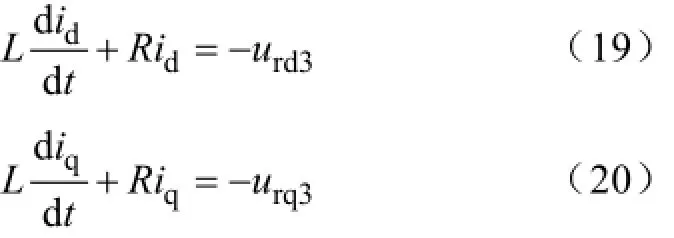
式（19）和式（20）表示的d、q电流子系统中，d、q轴电流是独立控制的，而且控制对象也很简单，相当于对一个一阶对象的控制。之所以能形成式（19）和式（20）这种简洁形式，其主要原因是引入了电流状态反馈（urd2和urq2）解耦。而引入了电网扰动电压（urd1和urq1）作前馈补偿，也使系统的动态性能有进一步提高。

图4是交叉解耦下高频PWM整流器双闭环控制结构的原理图。电压控制器和电压反馈构成外环，加入了前面分析的控制母线二倍频纹波参考给定，mudc是逆变器出电压的瞬时值vo，m为当前的调制比，是控制器已知量，这样就不需要检测逆变器输出电压，与逆变器输出电流相乘可以得到逆变器瞬时输出功率，这个功率与母线电压环输出的功率波动叠加后再除以vd则作为d轴电流指令，q轴电流指令根据是否需要发无功功率决定。电流控制器和电流反馈构成内环。

图4　PWM整流器控制框图

4　仿真结果

为验证本文提出方案的可行性，在Matlab/ Simulink中进行了仿真验证。仿真主要参数为：变压器原方输入线电压有效值6000V，二次侧线电压有效值均为630V，PWM整流模块直流母线电压给定为960V，系统容量为1.8MW，18个模块，单个模块100kW。有源模块整流器采用SPWM控制，开关频率为2100Hz，仿真中对有源整流模块SPWM控制的载波进行移相，移相角为360o/k，k为模块数量。模块逆变侧采用载波移相的控制方式，单极倍频SPWM调制，开关频率为350Hz。负载用功率因数为0.85的阻感负载。对有变压器漏感按平均分布计算，即每个模块的输入侧变压器漏感相等，仿真分析了变压器的漏感为5%的情况。

首先仿真了二倍频纹波控制策略前后有源模块母线电容纹波，此时母线电容8000μF。

由图5（a）可知，没有对二倍频纹波控制时，母线电容的纹波波动范围在935～985V之间，加入二倍频纹波控制以后，母线电容的纹波波动范围在955～965V之间，由原来的50V波动减小到10V左右，减小了母线电容纹波电压。

图6中（a）和（b）是二倍频纹波控制前后，PWM整流器的输入电流，图7是对应的FFT分析，二倍频纹波控制后PWM整流器输入电流变差，输入电流的THDi增加了10%。

图5　二倍频纹波控制前后母线电容纹波电压波形

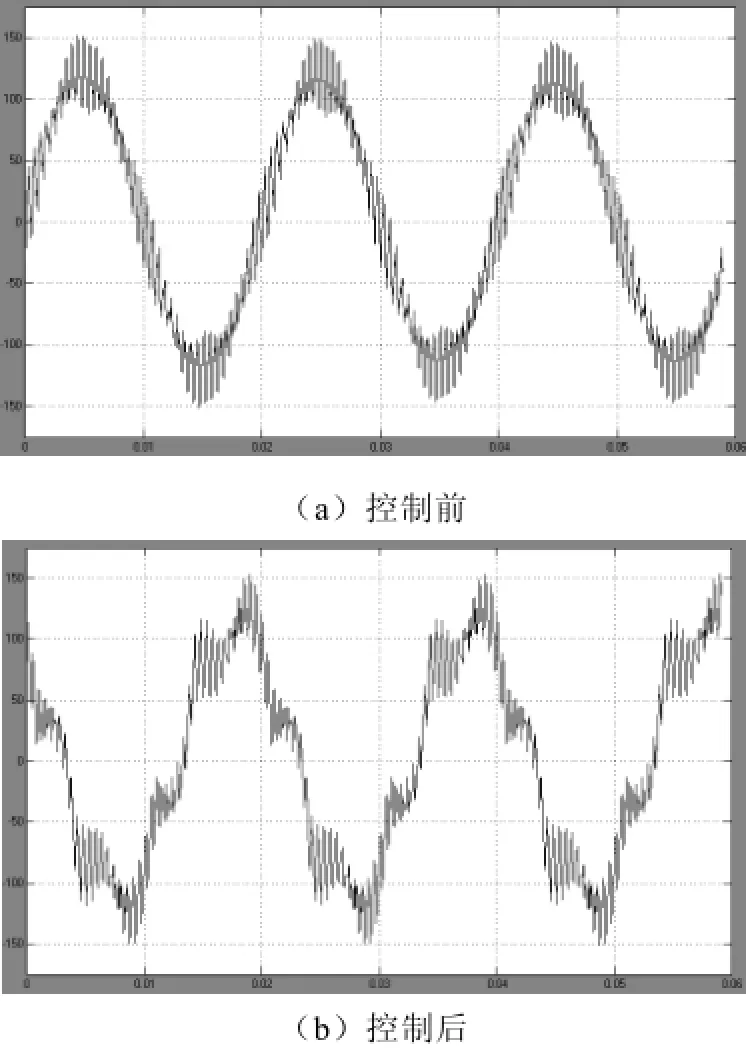
图6　二倍频纹波控制前后PWM整流器输入电流

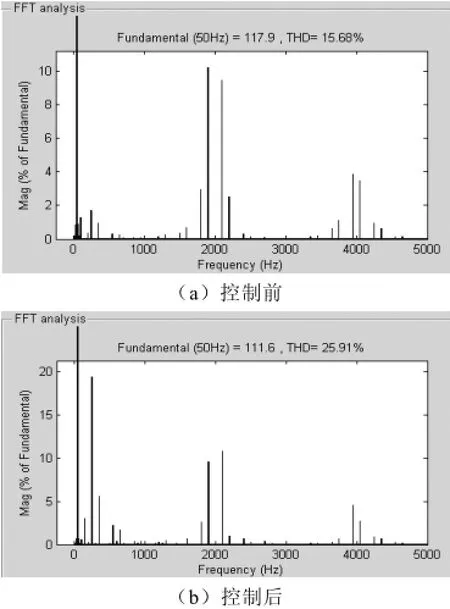
图7　二倍频纹波控制前后PWM整流器输入电流FFT分析

前面是没有减小母线电容的仿真结果，母线电容纹波电压被大幅抑制，图8是将母线电容进一步减小到5500μF后的仿真结果。

减小母线电容后，没有对二倍频纹波控制时，母线电容的纹波波动范围在920～990V之间，加入二倍频纹波控制以后，母线电容的纹波波动范围在950～970V之间，由原来的70V波动减小到20V左右，仍然远远小于母线电容8000μF不加二倍频纹波控制时的母线电压纹波。

图9中（a）和（b）是减小母线电容后加入二倍频纹波控后PWM整流器的输入电流和FFT分析，输入电流的THDi比减小母线电容前略有增加。

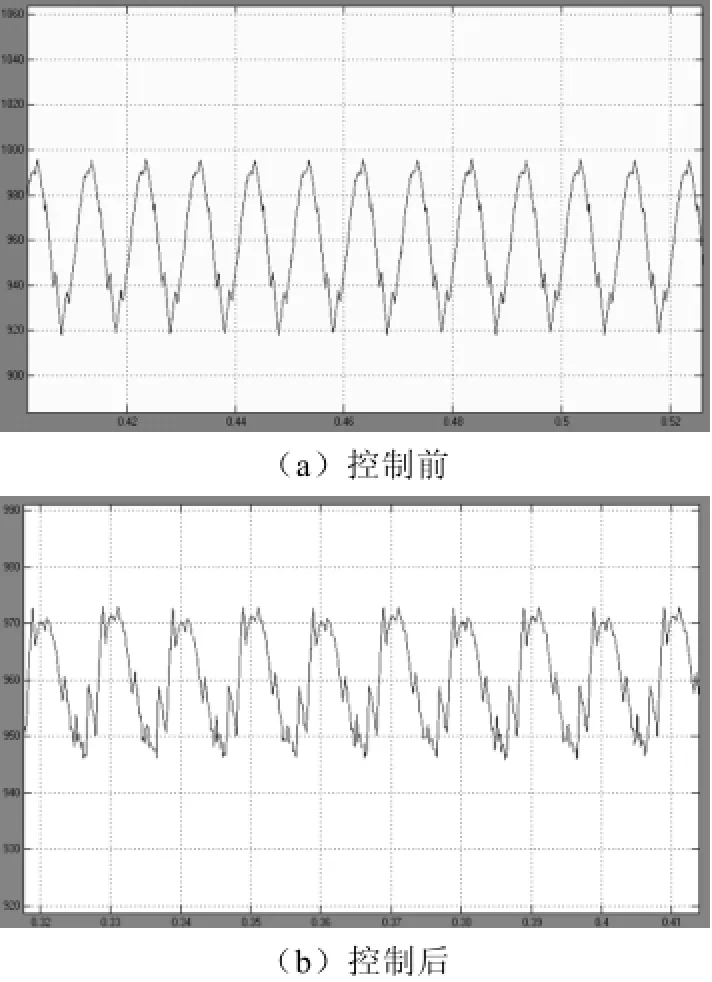
图8　二倍频纹波控制前后母线电容纹波电压波形（减小母线电容后）

图9 二倍频纹波控制在减小母线电容后PWM整流器输入电流几FFT分析

图10和图11是减小母线电容后，PWM整流器载波移相前后变压器原边输入电流分析，PWM整流器载波移相后，变压器原边输入电流的THDi也比较低，因为前面已经分析了，虽然PWM整流器输入电流的THDi较大，但是由于三相模块输入电流的谐波相抵消特性，原边输入电流THDi也不会很大，进一步采用载波移相处理后，变压器原边输入电流的THDi变得非常低。

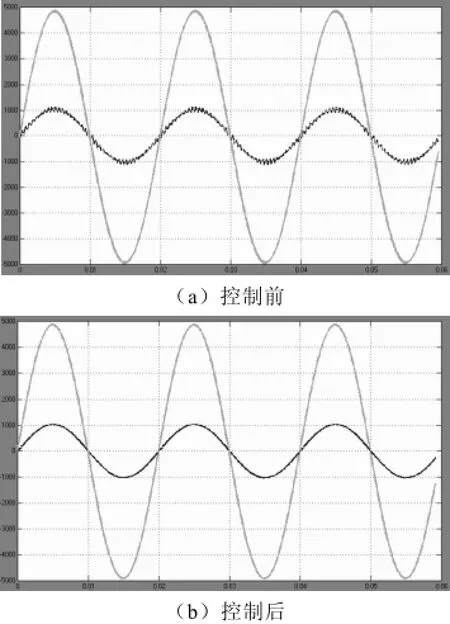
图10　PWM整流器载波移相控制前后变压器原边输入电流（减小母线电容后）

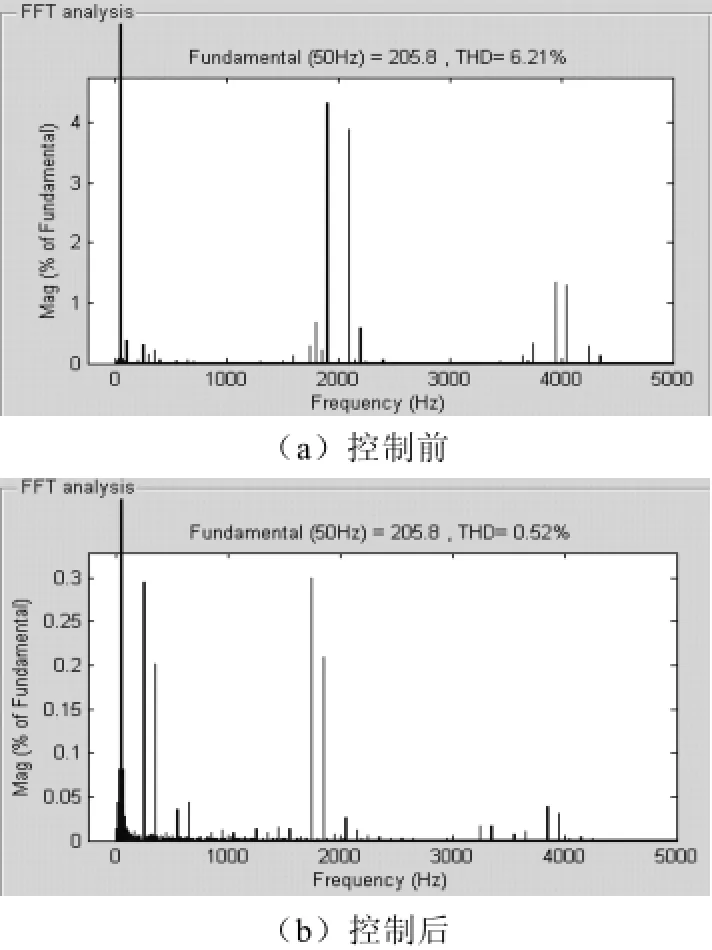
图11　PWM整流器载波移相控制前后变压器原边输入电流FFT分析（减小母线电容后）

5　结论

通过前面的理论分析和仿真验证结果可知，本文所提出采用变压器付边漏感作为PWM整流模块输入滤波电感的实现方式是可行的，通过对模块之间载波移相处理后进一步改善了变压器原边输入电流，文中所提出的减小母线电容二倍频纹波控制方案可以大幅降低母线电容的二倍频纹波，进而可以减小母线电容，减小了模块的体积和成本，虽然加入二倍频纹波控制后，PWM 整流模块输入电流变差，但是通过理论分析三相模块谐波相抵消特性和仿真结果证明，不会对变压器原边输入电流产生影响。

［1］ Z S MJ， Peng Fz. Multilevel converters-a new treed of power converters［J］. IEEE Transactions on Industry Application， 1996， 32（3）： 509-517.

［2］ Fang Zhengpeng， Jih-Sheng L， Mckeever JW， et al. A multilevel voltage-source inverter with separate DC sources for static VAr Generation［J］. Industry Applications， IEEE Transactions on， 1996， 32（5）： 1130-1138.

［3］ 丘东元， 张波， 潘虹. 级联型多电平变换器一般构成方式及原则研究［J］. 电工技术学报， 2005， 20（3）：24-29， 35.

［4］ 李永东， 饶建业. 大容量多电平变换器拓扑-现状与进展［J］. 电气技术， 2008（9）： 7-12.

［5］ 吴凤江， 赵克， 孙力， 等. 一种新型四象限级联型多电平逆变器拓扑［J］. 电工技术学报， 2008， 23（4）：81-86.

［6］ 王久和， 李华德， 李正熙. 电压型PWM整流器直接功率控制技术［J］. 电工电能新技术， 2004， 23（3）：64-67.

［7］ Wang Liqiao， Li Jianlin， Zhang Zhongchao. Carrier phase shifted SPWM based on current sourced multi-modular converter for active power filter［J］. Journal of Zhejiang University. Science， 2004， 5（7）：861-866.

［8］ 刘庆丰， 王华民， 刘丁. 级联型多电平逆变器中的谐波控制［J］. 电工技术学报， 2006， 21（10）： 38-43.

［9］ 熊健， 张凯， 陈坚. PWM整流器的控制器工程化设计方法［J］. 电工电能新技术， 2002， 21（3）： 44-48， 69.

The Method to Reduce DC Bus Voltage Ripple for Novel Four-Quadrant Cascade Multi-Level Inverter

Zhang Hongliang Zhou Peng
（Zhengzhou University of Aeronautics， Zhengzhou 450046）

In AC motor VSD area， Traditional cascade multi-level inverter is widely used， but this type of converter could not realize the energy regeneration， so used in limited area. Through integrating PWM rectifier into traditional H-bridge inverter， the cascade inverter could realize energy regeneration. But PWM rectifier module need filter inductance， this will increase the converter's space and cost， so it is also not widely used in application. The inverter side of cascade converter module is H bridge inverter，so the ripple of DC bus voltage is very large， this will also increase the converter's space and cost， This paper proposed a method of using transformer's leakage inductancce instead of filter inductance， This method can reduce system's space and cost. This paper also proposed a new method to reduced DC bus voltage ripple by controlling PWM rectifier， the DC bus capacitor and its cost can be reduced. The input current of PWM rectifier is deteriorated， but the three phase harmonic current can be canceled， so the harmonic current has no effect on transformer input current. The phase-shifted SPWM technology is used in the cascade inverter to reduce harmonious of input current. Analysis and simulation results indicated validity and feasibity.

cascade multilevel inverter； four-quadrant； PWM rectifier； phase-shifted carrier

河南省科技攻关计划项目（152102210137）

航空基金项目（2015ZD55005）

郑州航空工业管理学院青年基金项目（2015133001）

张宏亮（1978-），男，郑州航空工业管理学院讲师，主要从事电工电子技术教学及科研工作。