基于风速-功率拟合与区间潮流的风电场电压波动预测

吴丹岳　李兆祥，　邵振国

（1. 国网福建省电力有限公司电力科学研究院，福州 350007；2. 福州大学电气工程与自动化学院，福州 350016）

基于风速-功率拟合与区间潮流的风电场电压波动预测

吴丹岳1李兆祥1，2邵振国2

（1. 国网福建省电力有限公司电力科学研究院，福州 350007；2. 福州大学电气工程与自动化学院，福州 350016）

风机发电功率具有明显的波动性，将造成电网电压波动。根据历史风速数据预测风电接入可能造成的电压波动量，有助于选择最优的入网点或配置治理方案。本文提出一种基于区间运算的预测方法，根据风速数据预测风电机组接入后的电网节点波动量。首先建立风力发电机的最大风能跟踪控制和有功、无功解耦控制模型，从仿真数据拟合风速与风力发电功率的关系模型，预测风力发电功率的变化区间。此后基于高斯-塞德尔迭代法求解区间潮流方程，最后根据节点电压区间值预测风电机组并网运行后造成的电压波动量。采用蒙特卡罗随机潮流验证了本文方法的有效性和正确性。

风力发电；电压波动；区间潮流算法；电能质量

由于风速、风向等自然环境因素的时刻变化，注入电网的风电功率具有明显的波动性、随机性和不可控性等特点，分布式发电用户对电网运行的影响不容忽视［1］。

从节点电压能够检测分布式发电设备造成的电压波动和闪变［2-3］，通过在线辨识用户运行参数可以评估单个用户的注入污染量［4］，两者都可以为电网运行管理提供电能质量实时信息。而在新增用户入网选址时，必须将电压波动作为约束条件参与优化，因而需要对分布式发电用户接入电网造成的电压波动进行预判。这是电能质量监测或注入评估均无法解决的问题。

本文提出一种基于区间运算的预测方法，根据风速数据预测风电机组接入后的电网节点波动量，可以为风电接入选址提供参考。首先建立风力发电机的最大风能跟踪控制和有功、无功解耦控制模型，从仿真数据拟合风速与风力发电功率的关系模型，预测风力发电功率的变化区间。此后基于高斯-塞德尔迭代法求解区间潮流方程，最后根据节点电压区间值预测风力发电机组并网运行后造成的电网节点电压波动量。

1　风速-风电功率关系模型

目前较常用的风电场功率预测方法有时间序列法、物理建模法、风机功率统计建模法等。时间序列法只需有限样本即可建立高精度模型，但存在低阶模型误差大，高阶模型参数估计难的问题［5］。物理建模法无需历史数据，但需要建立风电场模型并获取准确性较高的天气预报数值［6］。统计建模法使用数据单一，计算速度快，但需要大量的历史数据。本文以变速恒频风电系统为分析对象，从风功率、风机功率控制、仿真建模等角度分析得到双馈式风机非线性工作区下的风速-功率曲线，然后估计某风速区间下的风机输出功率波动区间。

1.1风电机组输出功率

当空气密度为ρ的气流以速度νw穿过面积为A的区域时，风机从中捕获到的风功率Pw如式（1）所示［7］。

叶尖速比λ与外界风速νw满足如下关系

式中，ωtur是风力机叶轮的角速度。

由贝兹理论可知，风能利用系数Cp与桨距角β、叶尖速比λ等因素密切相关，其公式可描述成

式中，常数K1～K9需根据风力机实际情况调整。

设发电机电力转换效率为ηg，风力机机械传动效率为ηt，则风力发电机输出功率为

1.2风电机组建模

双馈式风力发电机的功率控制模块主要分为最大风能跟踪控制和有功、无功解耦控制两部分。

风能利用系数Cp和叶轮转速ωtur的关系曲线如图1所示。当桨距角β 为常数时，令y=1/λt，化简式（3）并对其求导

由式（5）可知，桨距角恒定时，风能利用系数Cp将取决于叶尖速比λ，且存在最大值。因此，在风机转速不超过限值的情况下，只需根据当前实测风速求得最优风机转速，即可使得风力发电机能量转换效率达到最大值Cp-max。以风机实际转速与最优转速的偏差作为控制输入量，即可简单地实现最大风能跟踪控制［7-8］。

图1　风能利用系数Cp与转速ωtur关系曲线

根据以上思路，在PSCAD建立双馈风机的风能跟踪仿真模型，风速曲线如图2（a）所示。当桨距角β=10°时，最大风能跟踪控制下的风机转速及Cp值分别如图2（a）、（b）所示。由Cp曲线可知，最大风能跟踪控制能够使得风能利用系数保持恒定值。

采用定子磁链矢量定向控制可实现风机输出功率的有功、无功解耦［9-11］，使得输出有功功率只与转子电流q轴分量irq有关，输出无功功率只与转子电流d轴分量ird有关。在PSCAD中建立有功、无功解耦控制模型，仿真结果如图3所示。从图3（b）上可以看出，功率解耦控制实现了恒功率因数运行。

1.3风速-风电功率曲线拟合

如图4所示，风力发电机的典型运行状态可分为启动并网区、非线性区、恒功率区及停机脱网区。当外界风速νw小于切入风速νcut-in，风机会脱离电网；当风速νw在区间（νcut-in，νN）内时，风机处于变速运行状态，并通过捕捉外界风速值实现最大风能跟踪控制；当风速vw大于额定风速vN后，风机将受到发电机和换流器等元件的容量限制，不能将盈余的风能输出到电网。

根据运行仿真数据或者风电机组的历史运行数据，拟合风电机输出功率与风速的关系模型，即可预测风力发电机组的入网功率。由图2（b）可知，当风速νw∈（νcut-in， νN）时，且风机桨距角为常数时，风能利用系数可视为恒定值。因此本文在建立双馈式风机运行模型以后，仿真得到不同类型风速下的风电输出有功功率，采用式（6）的三次函数模型拟合风速-功率曲线，结果如图5所示。

图3　双馈式风机功率解耦控制仿真结果

图4　典型风机输出功率曲线

图5　风速-风电功率拟合曲线

由图5可以看出，三次函数模型能够很好地拟合风电-风电功率曲线。仿真数据与拟合结果对比见表1，从表上可见，采用拟合关系模型来预测风机输出功率的区间范围是可行的。

表1　仿真结果及拟合曲线对比

2　电压波动计算

本文将风电机组入网功率表示为边界值确定的区间量，建立区间潮流方程后进行高斯-赛德尔迭代，按照区间数的运算法则计算电网节点电压的变化范围。

2.1区间数及其运算法则

对于给定的数对x1、x2∈R，若满足x1≤x2关系，则有界闭区间［X］如式（7）所示，其中，x1、x2分别称为区间［X］的下端点和上端点［12］。

若区间的上、下端点数值相等，即x1=x2，则区间［X］被定义为点区间。

在有界闭区间［X］里，到上、下端点的距离相等的点，称为区间的中点mid（［X］），其定义式如下：

区间中点到任意端点的距离称为区间的半径Rad（［X］）。

有界闭区间［X］也可以表示为

复区间数［Z］的圆形域表达式如式（11）所示［13］，其中中点mz=xz+jyz，半径为rz。

复区间数的四则运算如式（12）至式（14）定义。

2.2区间潮流迭代求解

电网节点功率方程如式（15）所示。

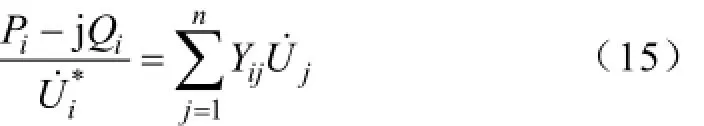
恒定负荷在监测周期内表示为点区间数。波动性负荷的区间数包括负荷功率的中心值及变化半径。

设节点i接有x个恒定负荷和y个波动性负荷，则Si可记作

由此，基于高斯-塞德尔迭代法拓展得到的区间潮流迭代方程式如式（17）所示。其中线路阻抗、变压器阻抗、负荷功率等参数均可采用区间数。

考虑到节点电压区间值只与负荷功率波动相关，因此在上式右端只保留上一次迭代得到的节点电压中点值。

式（18）迭代的收敛条件如式（19）所示。

节点电压波动如式（20）计算，其中节点电压幅值的最大值Uimax和最小值Uimin为节点电压区间值的上端点和下端点。

3　电压波动预测算例

设一简单的风电接入系统如图6所示，三台风力发电机分别经过升压变压器连接到PCC点。基准值SB=10MVA，图中A、B、C区三台升压变压器在稳定运行状态下变比的标幺值分别为ka=1∶1.0125、kb=1∶1.05、kc=1∶1.025，变压器阻抗的标幺值分别为Xa=0.10、Xb=0.105、Xc=0.12。各线路阻抗分别为Z1=0.025+j0.08、Z2=0.0375+j0.12、Z3=0.0185+j0.06、Z4=0.0125+j0.04，系统短路阻抗Zs=0.0141+j0.0989。

A、B、C三处的风速变化分别如图7所示，根据风速-功率曲线计算三台风力发电机的输出功率区间，结果见表2。此后采用区间潮流算法计算出各节点的电压区间值见表3，程序运行费时2.7s左右。

图6　简单风电系统

表2　关系模型下的A、B、C区风电功率区间值

表3　两种方法的电网节点电压波动计算结果

采用蒙特卡洛抽样模拟算法来验证区间算法的可行性。由图7所示风速曲线分别仿真得到A、B、C区的风电功率，视作三组相互独立的变量，进行10000次随机抽样计算电网潮流，统计得到各节点电压的最大值、最小值，程序运行费时78s左右。

图7　A、B、C区风速曲线

由此可知，电压波动区间预测算法计算时间短，且计算结果与蒙特卡罗模拟法结果较为接近，能够较为真实地反映多个波动负荷对电网电压波动的影响。

由于区间预测算法涵盖了所有风速工况组合下的潮流结果，因而区间预测算法的节点电压波动范围包含了蒙特卡罗模拟法的计算结果，因此区间预测算法比蒙特卡罗模拟法更全面。

4　结论

风速的随机变化是影响风电机组输出功率频繁波动的主要原因，建立风速与风电机组功率的关系模型，有助于预测风电机组输出功率的波动范围。本文在拟合出风速-风机输出功率曲线以后，建立了区间潮流方程，并采用高斯-塞德尔迭代算法求解节点电压波动量，能够预测风电接入造成的电压波动大小。

与蒙特卡罗随机潮流计算电压波动量相比较，文中方法计算时间短，且结果涵盖了全部运行工况，更适用于预测组合工况多、用户参数不确定情况下的电网电压波动。但随着电网节点数的增加，高斯-塞德尔迭代次数也会增大，甚至出现不收敛的状况。此外计算次数大还会造成计算误差累计，导致超宽度的产生，影响预测评估的正确性和有效性。采用高效的迭代算法并引入区间算法约束条件，将有助于提高算法的收敛性和预测精度。

［1］ 田春筝， 李琼林， 宋晓凯. 风电场建模及其对接入电网稳定性的影响分析［J］. 电力系统保护与控制，2009， 37（19）： 46-51.

［2］ 王继东， 刘琨， 高彦静. 基于瞬时无功功率理论的电压波动检测和闪变计算［J］. 电力系统保护与控制，2012， 40（2）： 145-150.

［3］ 苏刘军， 鲁宝春， 李昌超， 等. 一种改进的无锁相环三相电压波动检测方法［J］. 电力系统保护与控制，2014， 42（8）： 121-126.

［4］ 苏清梅， 张嫣， 邵振国. 基于波动模型及虚拟场景评价的闪变污染用户危害评估［J］. 电力系统保护与控制， 2013， 41（23）： 97-102.

［5］ 朱晓荣， 刘艳萍. 基于稳健估计时间序列法的风功率预测［J］. 电力系统及其自动化学报， 2012， 24（3）：107-110， 126.

［6］ 冯双磊， 王伟胜， 刘纯， 等. 基于物理原理的风电场短期风速预测研究［J］. 太阳能学报， 2011， 32（5）：611-616.

［7］ 刘其辉， 贺益康， 赵仁德. 变速恒频风力发电系统最大风能追踪控制［J］. 电力系统自动化， 2003，27（20）： 62-67.

［8］ 马祎炜， 俞俊杰， 吴国祥， 等. 双馈风力发电系统最大功率点跟踪控制策略［J］. 电工技术学报， 2009，24（4）： 202-208.

［9］ 林成武， 王凤翔， 姚兴佳. 变速恒频双馈风力发电机励磁控制技术研究［J］. 中国电机工程学报， 2003，23（11）： 122-125.

［10］ 高江魁， 王涛， 陈力， 等. 基于PSCAD的双馈风力发电机的仿真建模及特性分析［J］. 电气自动化，2014， 36（2）： 45-47， 50.

［11］ 兰华， 刘座铭， 童建东， 等. 双馈风力发电机空载并网控制策略研究［J］. 继电器， 2008， 36（10）： 11-14， 18.

［12］ 王德人， 张连生， 邓乃扬. 非线性方程的区间算法［M］. 上海： 上海科学技术出版社， 1987.

［13］ 王守相， 张国栋， 王成山. 复区间潮流保守性问题的解决方案［J］. 电力系统自动化， 2005， 29（19）：25-30.

［14］ 杨欢， 邹斌. 含相关性随机变量的概率最优潮流问题的蒙特卡罗模拟方法［J］. 电力系统保护与控制，2012， 40（19）： 110-115.

［15］ Feijóo A， Cidrás J， Carrillo C. A third order model for the doubly-fed induction machine［J］. Electric Power Systems Research， 2000， 56（2）： 121.

［16］ Xing Zuoxia， Liang Lizhe， Guo Hengyi， et al. Damping control study of the drive train of DFIG wind turbine［C］// ICEET： 2009 INTERNATIONAL CONFERENCE ON ENERGY AND ENVIRONMENT TECHNOLOGY，VOL 1， PROCEEDINGS， 2009： 576-579.

［17］ Estanqueiro AI. A dynamic wind Generation model for power systems studies［J］. IEEE Transaction on Power Systems， 2007（3）： 920-928.

Calculating the Voltage Fluctuation based on Wind Velocity-wind Power Fitting and Interval Power Flow for Wind Farm

Wu Danyue1Li Zhaoxiang1,2Shao Zhenguo2
（1. Electric Power Research Institute of Fujian Electric Power Co.， Ltd， Fuzhou 350007；2. College of Electrical Engineering and Automation， Fuzhou University， Fuzhou 350016）

The power fluctuation of wind generator would cause voltage fluctuation on the power grid. Voltage fluctuation prediction based on historical measurements of wind speed is useful for the optimal choice of grid-connected node or governance method. This paper introduces an assessment method based on interval arithmetic. According to historical measurements of wind speed， this method could estimate the voltage fluctuation caused by the wind farm. Study the maximum power point tracking method and the active power and reactive power decoupling control， then build the simulation model of DFIG to get the relation function between wind speed and output power of DFIG with fitting method. With the predicted interval value of wind turbine output， figure out the voltage fluctuation by solving the interval iteration equations which are based on Gauss-Seidel algorithm. Verify the validity and feasibility of this method by Monte-Carlo probabilistic load flow.

wind power generation； voltage fluctuation； interval power flow； power quality

福建省科技计划重点项目（2013H0024）

吴丹岳（1964-），男，硕士，高级工程师，研究方向为电能质量。