Model Updating for High Speed Aircraft in Thermal Environment Using Adaptive Weighted-Sum Methods
2016-09-06HeHuanHeChengChenGuoping
He Huan, He Cheng, Chen Guoping
1.The State Key Lab of Mechanics and Control for Mechanical Structures,Nanjing University of Aeronautics and Astronautics, Nanjing 210016, P.R. China;2.Research Institute of Pilotless Aircraft, Nanjing University of Aeronautics and Astronautics,Nanjing 210016, P.R. China
(Received 31 February 2015; revised 13 April 2015; accepted 18 April 2015)
Model Updating for High Speed Aircraft in Thermal Environment Using Adaptive Weighted-Sum Methods
He Huan1, He Cheng2*, Chen Guoping1
1.The State Key Lab of Mechanics and Control for Mechanical Structures,Nanjing University of Aeronautics and Astronautics, Nanjing 210016, P.R. China;2.Research Institute of Pilotless Aircraft, Nanjing University of Aeronautics and Astronautics,Nanjing 210016, P.R. China
(Received 31 February 2015; revised 13 April 2015; accepted 18 April 2015)
Model updating for aircraft in a high temperature environment (HTE) is proposed based on the hierarchical method. With this method, the problem can be decomposed into temperature field updating and dynamic structural updating. In order to improve the estimation accuracy, the model updating problem is turned into a multi-objective optimization problem by constructing the objective function which combined with residues of modal frequency and effective modal mass. Then the metamodeling, support vector regression (SVR) is introduced to improve the optimization efficiency, and the solution can be determined by adaptive weighted-sum method (AWS). Finally, the proposed method is tested on a finite element (FE) model of a reentry vehicle model. The results show that the multi-objective model updating method in HTE can identify the input parameters of the temperature field and structure with good accuracy.
hierarchical; high temperature environment (HTE); support vector regression (SVR); multi-objective optimization; model updating
0 Introduction
The United States is developing scramjet engine technology that is expected to be needed by the next generation of high speed air breathing vehicles. NASA, through the X-43A program, is developing hydrogen fueled scramjet engines and has demonstrated Mach number of approximately 7 to 10. The structural integrity of proposed high-speed aircraft can be seriously affected by the extremely high surface temperatures and large temperature gradients throughout the vehicle′s structure, which can seriously affect the struc-ture′s elastic characteristics. Fortunately, the finite element (FE) method, as a important and practical numerical analysis tool, can be used to simulate dynamic characteristics of structural. Hence, the accuracy of FE model is crucial for structural dynamic analysis.
On the one hand, the complexity of dynamic analysis in high temperature environment (HTE), caused by the thermal effects, has made it difficult to directly establish an accurate dynamic model; on the other hand, the FE model of a structure is normally constructed on the basis of highly idealized engineering blueprints and designs that may not truly represent all the aspects of an actual structure. As a result, the analytical predictions from a FE model often differ from the results of a real structure. These discrepancies originate from the uncertainties in simplifying assumptions of structural geometry, materials as well as inaccurate boundary conditions. FE model updating is a viable approach to increase the correlation between the dynamic response of a structure and the predictions from a model. This method based on residuals between a measurement set and the corresponding model predictions to adjust the uncertain parameters of FE models by optimization approach. Typical experimental datas include the modal model (natural frequencies and mode shapes), the frequency response functions and effective modal mass. The choice of objective function, and also the optimization approach, have been the subject of much research and are well covered by the authors′ survey paper[1-2].
If the structure of interest is represented by, e.g. a large FE model, the large number of computations involved can rule out many approaches due to the expense of carrying out many runs. In addition, the FE analysis programs at present do not have parameterized modeling function since the parameters need to be updated in the estimation process. To overcome those problem, we have focused on using metamodels (or surrogate models) that can mimic the behavior of the simulation model as closely as possible while being computationally very efficient and convenient to evaluate since the objective function have be parameterized. Amongst existing metamodels, such as the conventional response surface method[3], radial basic function[4]neural networks[5]and support vector regression (SVR)[6], the latter are found to be excellent predictors of numerical model behaviour with small samples. In recently, many additional applications (largely a consequence of the increased use of computational analyses) have broadened the range of application of SVR in the statistical and engineering literature.
Structural model parameter estimation problems based on measured modal data (e.g Ref.[5—7]) are often formulated as weighted least-squares problems in which modal metrics, measuring the residuals between measured and model predicted modal properties, are build up into a single weighted modal residuals metric formed as a weighted average of the individual modal metrics using weighting factors. Standard optimization techniques are then used to find the optimal values of the structural parameters that minimize the single weighted residuals metric representing an overall measure of fit between measured and model predicted modal properties. Due to model error and measurement noise, the results of the optimization are affected by the values assumed for the weighting factors. The choice of the weighting factors depends on the model adequacy and the uncertainty in the available measured data, which are not known a priori. Different values of the weights result in different optimal models and consequently different predictions from the optimal models.
In this work, the structural model updating in HTE using multi-objective optimization method is proposed. As one of metamodels, support vector regression (SVR), will be introduced to improve the efficiency of estimation, and adaptive weighted-sum method (AWS), as a multi-objective optimization method, is employed to update the structural parameters in HTE.
1 Hierarchical Methodology in Model Updating of High-Temperature System
1.1Model updating of temperature field
It is well know the mechanical and thermal aspects are coupled and inseparable: high surface temperatures and large temperature gradients will affect the modal characteristics of the structure. Similarly, the temperature distribution of a structure can also vary with its deformation, but this change are so slightly that Nowinski[8]suggested discounting the coupling in practice and separately evaluating the temperature and deformation fields in this order. Cheng et al. have proposed an model updating method in HTE based on hierarchical ideology. With this method, the temperature field updating of a structure is taken as the first stage, and the temperature distribution achieved from the former is imposed on the structure as a thermal load to complete the model updating in HTE. The thermo-physical properties are the important factors that affect temperature distribution of structure. In the case of thermal loads are determined, the model updating problem of temperature distribution model can be translated into the estimation of thermo-physical parameters problem.
Inverse parameter estimation methods are based on the minimization of an objective function containing both estimated and measured temperatures. Ordinary least squares estimator is by far the most frequently used method for the estimation of thermo-physical parameters as no prior knowledge is needed, therefore, the optimization problems can be formalized as follows
(1)
1.2Model updating of dynamic structure in HTE
As discussed before, the dynamic responses in HTE, which can be expressed as[9]
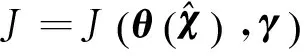
(2)
For model updating techniques, either identified modal parameters such as eigenvalues and eigenvectors or measured frequency response functions (FRFs) are widely used as reference data[10-11]. In recent years, some new dynamic parameters have also been used in the model updating. Aerospace engineers make wide use of the effective modal mass concept in structural spacecraft design[12].The effective modal mass,as is known, represents the participation of an elastic mode to the reaction at the junction and therefore the knowledge of such a parameter is useful for the analysis of the dynamic behaviour of satellites and aerospace substructures coupled with the launcher. Therefore, the effective modal mass, as a complement could provide more information for model updating to reduce the ill-posed problem which caused by the errors arise form uncertainties.
The model updating problem has recently been formulated in a multi-objective context[13]that allows the simultaneous minimization of the multimodal indicators, which include eigenvalues, eigenvectors and effective modal mass, etc. Then, the problem of model updating for identifying the model parameter values that given the best fit in all groups of modal properties can be formulated as a multi-objective optimization problem. In this work, the multi-objective model updating method based on residuals of modal frequency (ω) and effective modal mass (M) are introduced, the multi-objective optimization problem can be written as
(3)
(4)
Although the weighted-sum approach is simple to understand and easy to implement, the traditional weighted-sum approach has two main drawbacks which are hard to avoid[14]: First, an even distribution of the weights among objective functions does not always result in an even distribution of solutions on the Pareto front; Second, the weighted-sum approach cannot find solutions on non-convex parts of the Pareto front, although such non-dominated solutions (Pareto optimal solutions) do often exist. For that reasons, Kim[14]propose a new adaptive method, based on the weighted-sum approach, for multi-objective optimization—adaptive weighted-sum method (AWS). In this approach, the weights are not predetermined, but they evolve according to the nature of the Pareto front of the problem. The AWS algorithm produces an even spread of points along the Pareto front, even for problems for which the relative scaling of the objectives are vastly different. Firstly, the uniform step size of the weighting factorΔλ is determined. By using a large step size of the weighting factor,Δλ, a coarse representation of the solution is generated and regions where more refinement is needed are identified. The specific regions are then designated as a feasible region for sub-optimization by imposing inequality constraints in the objective space. In this region, the typical weighted-sum multi-objective optimization is performed. The algorithm will terminates when all the regions of the Pareto front reach a pre-specified resolution. More details about the AWS method in terms of advantages and drawbacks can be found in Ref.[14].
2 Overview of Support Vector Regression
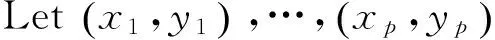
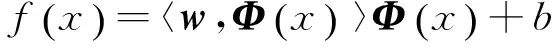
(5)
When the identity function is used, i.e.Φ(x)→x, no transformation is carried out, and linear SVR models are obtained.

(6)
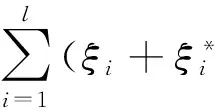
(7)
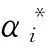
(8)

(1) Polynomial:k(x,xi)=((x,xi)+c)p,p∈R,c≥0;
(2) Gaussian:k(x,xi)=exp[-|x-xi|2/σ2];
(9)
(3) Exponential:k(x,xi)=exp(-a|x-xi|),a>0;
The penalty coefficient c can be determined by cross validation method.
3 Numerical Examples and Discussion
The FE model of reentry vehicle structure in an HTE will be used as an example to check the feasibility of the multi-objective identification method for structural model updating methodology proposed in this paper, as shown in Fig.1. A simplified system of the reentry vehicle and its internal structure, by assuming that the aircraft is in the sub orbital flight and will be subjected to extremely high surface temperatures and large temperature gradients. The model comprises two parts: the surface of reentry vehicle is made by ceramic matrix composites (C-SiC) and internal structure made of oxide dispersion strengthened super alloys (PM1000), both of them are exist in inside and outside of the structure in order to withstand the high temperatures generated by aerodynamic heating, interlayer with reinforcing ribs connected. The ambient temperature is 20 ℃, and we ignore the influence of installation location of bolts at the specimen on the temperature distribution.
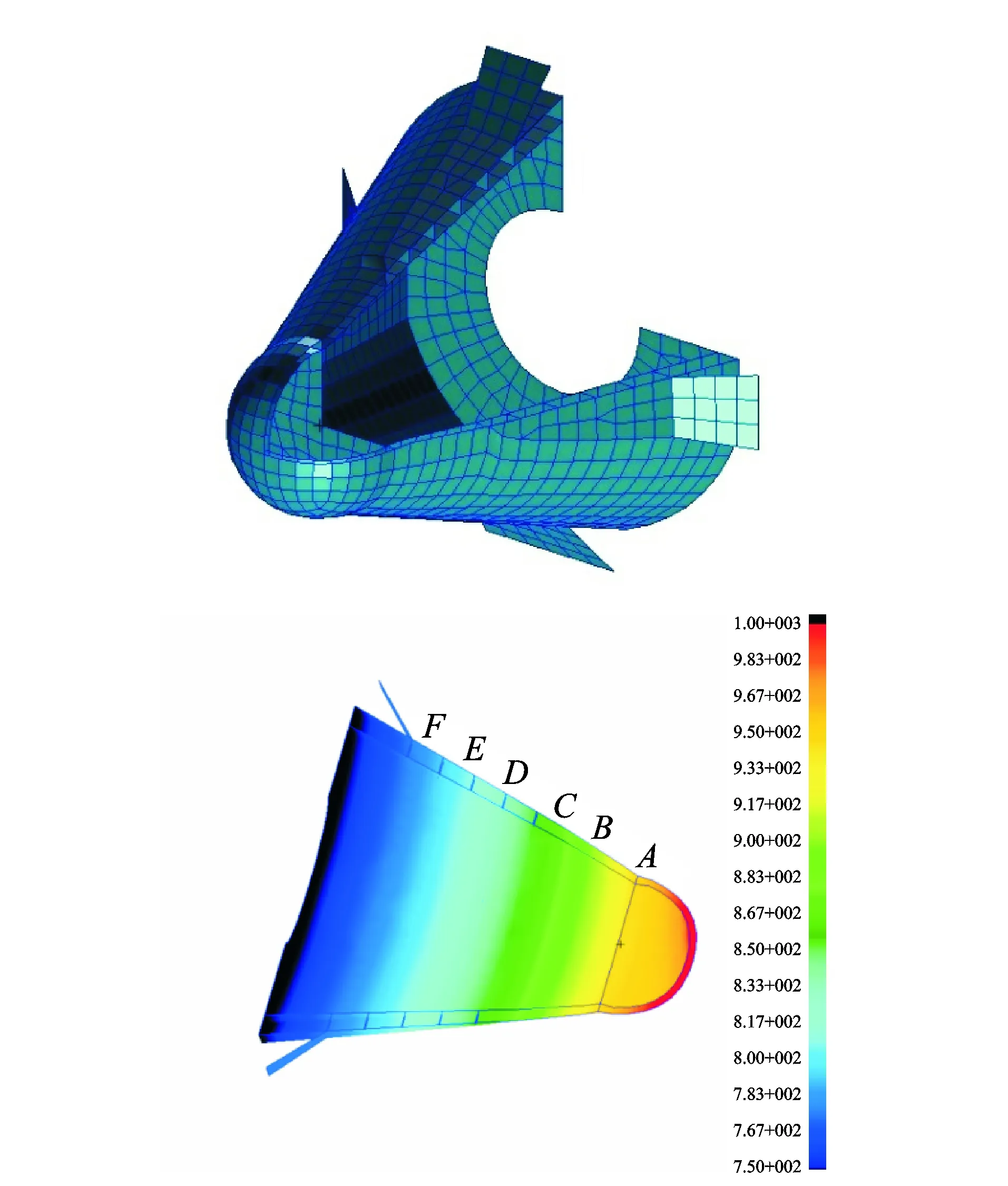
Fig. 1 Temperature distribution of reentry vehicle and its cutaway view of FE model
It is possible to imagine many different parameterizations for updating the FE of the reentry vehicle structure. In this paper, the heat transfer derivative of cone and pyramidal structure, χ1and χ2, are chosen as the updating parameters, which have significantly effects on temperature distribution of the reentry vehicle by using sensitivity analysis. Similarly, the elastic modulus of cone E1and thickness of pyramidal structure t2are chosen as updating parameters for structural dynamic model updating. Then, we will employ the SVR-GS to update the FE model of thermal transfer and dynamic structures, respectively, based on hierarchical method in HTE proposed by Ref.[9] once they are confirmed to be updating parameters.

Table 1 Initial design space of thermal parameters modific
Table 1 shows the initial design space of thermal parameters by trying. The normalization process is described as transition from the original interval [x1i,x2i] of the design variables xito the new interval [-1, 1] of the design variables yi, where i=1,2,…,k for convenience. Assume that the target values of required thermal correction parameters are α1=0.3 W/mm and α2=0.2 W/mm, which are used to calculate temperature distribution as the real value. Pick up 16 sample points randomly using the Latin hypercube design in the initial design space of thermal parameters, and calculate the temperature value as the theoretical value. Approximately substitute the SVR-GS surrogate models for the relation between objective function and design variables. The temperature residual model is shown in Fig. 2 in the form of SVR-GS. Then we get the optimal solution by the genetic algorithm owing to their excellent performance in the global optimization problem. The updated thermal parameter values are shown in Table 2.
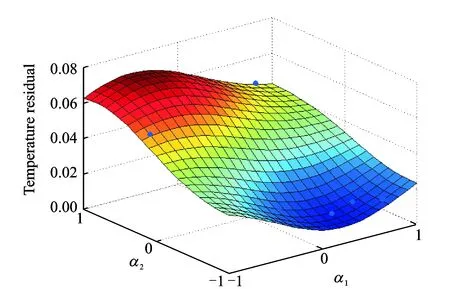
Fig. 2 SVM-GS surrogate model

Table 2 Modified thermal parameter values
Table 3 shows the temperature deviations before and after modification for A, B, C, D, E, F (Fig. 1) six points. We found that the largest temperature deviation based on the SVM-GS model is no more than 0.909 9%, which indicates
that the temperature distribution of vehicle calculated by the updated parameters agrees well with the true temperature distribution. Then, the process of structural dynamics model updating is conducted based on the updated steady-state temperature distribution. The 16 sample points are selected randomly by the Latin hypercube design in the initial design space of each thermal parameter, and the first fourth-order natural frequency is calculated as the theoretical value. Assume that E1=90 GPa and t2=3 mm are the error resource of structural dynamics parameters needed to be updated, and calculating the first fourth-order natural frequency of vehicle in HTE as experimental values based on the ture values. The residuals of the theoretical value and the experimental value of each order natural frequency and effective modal mass are built by Eq.(3), respectively. Similarly, the SVM-GS predictor of objective function in Eq.(3) could be established to estimate the elastic modulus (E1) and thickness (t2). The identified Pareto curve is composed of 15 Pareto optimal solutions and shown in Fig. 3 by using the AWS described above.
Tables 3—4 present the updated parameters and the errors of reentry vehicle dynamic characteristic using AWS. It is observed that the maximum error of updated parameters is no more than 2.727%, and the maximum error of updated frequency is no more than 2.9%. There are slight differences between the parameters of the updated model and the test ones, which indicates that the model updating method proposed in this paper is available for practical applications.
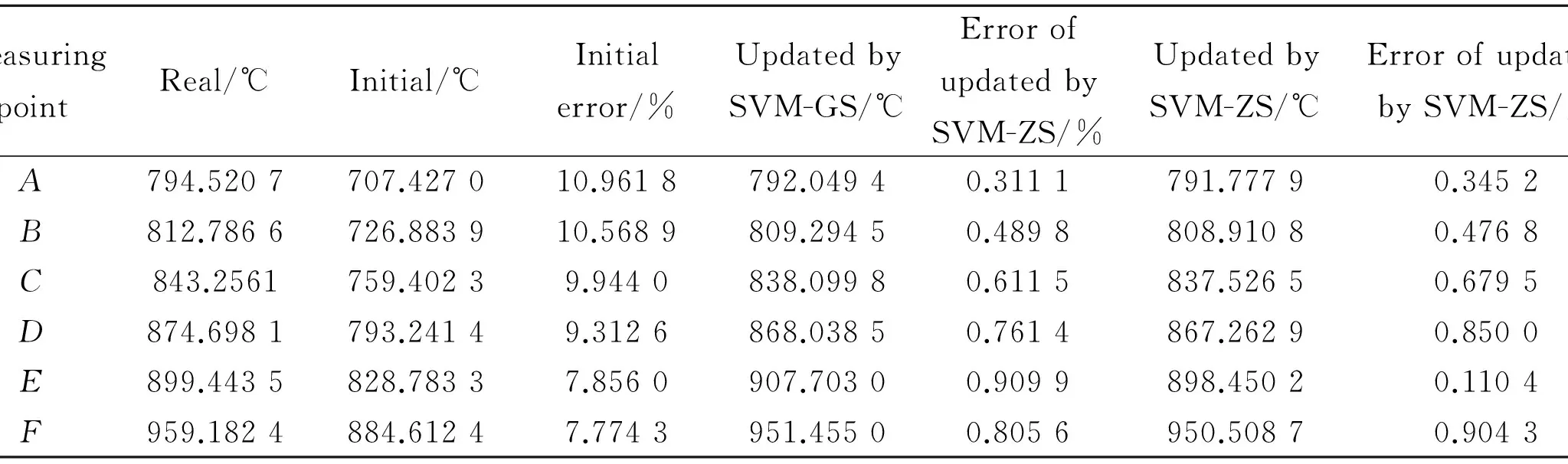
Table 3 Comparison of test frequencies with updated temperature
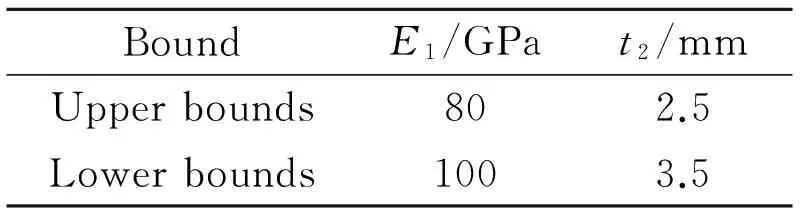
Table 4 Initial design space of dynamic structural updating parameters
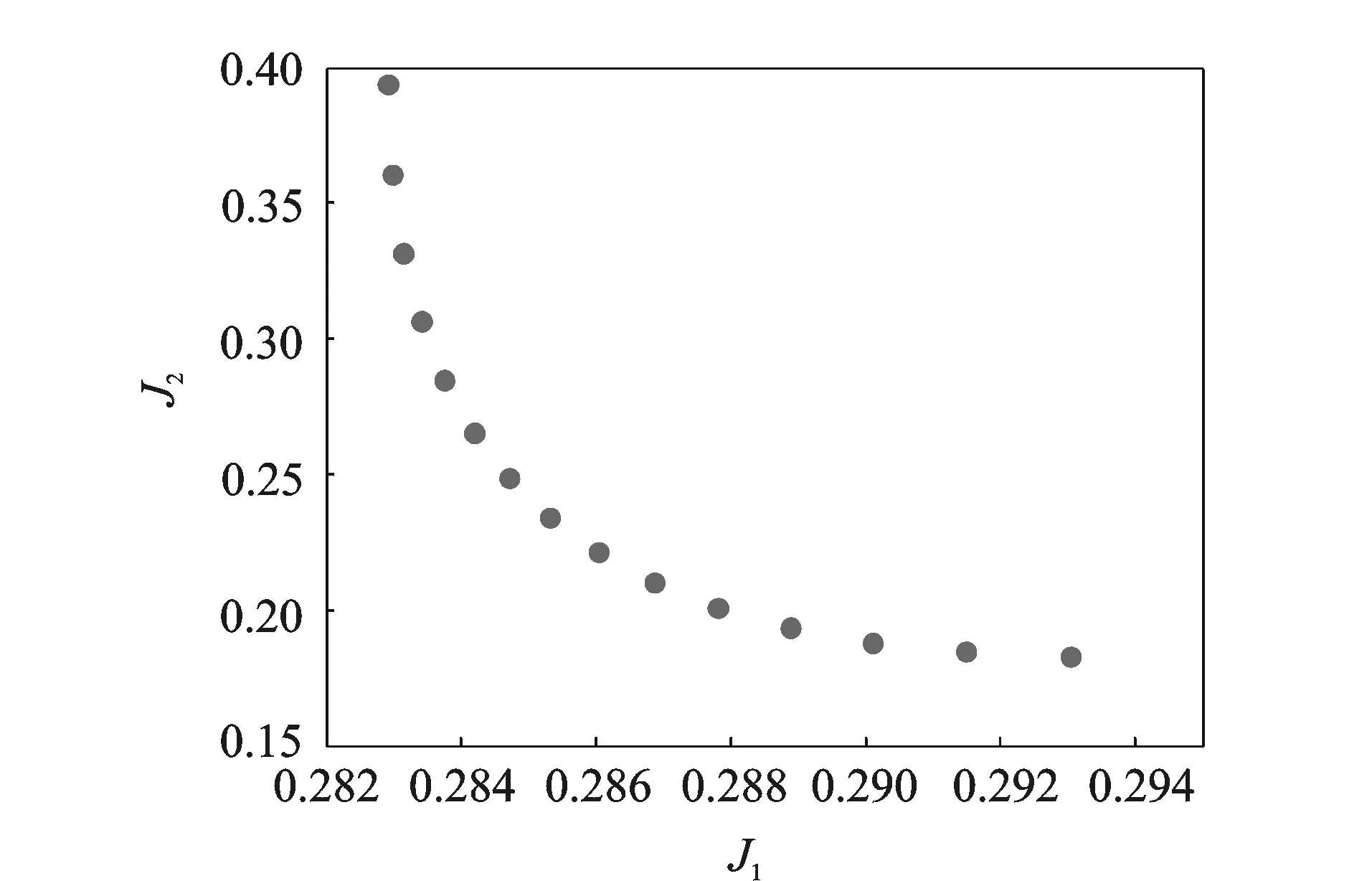
Fig. 3 Pareto frontier calculated by AWS

Table 5 Comparison between updated parameters and real parameters
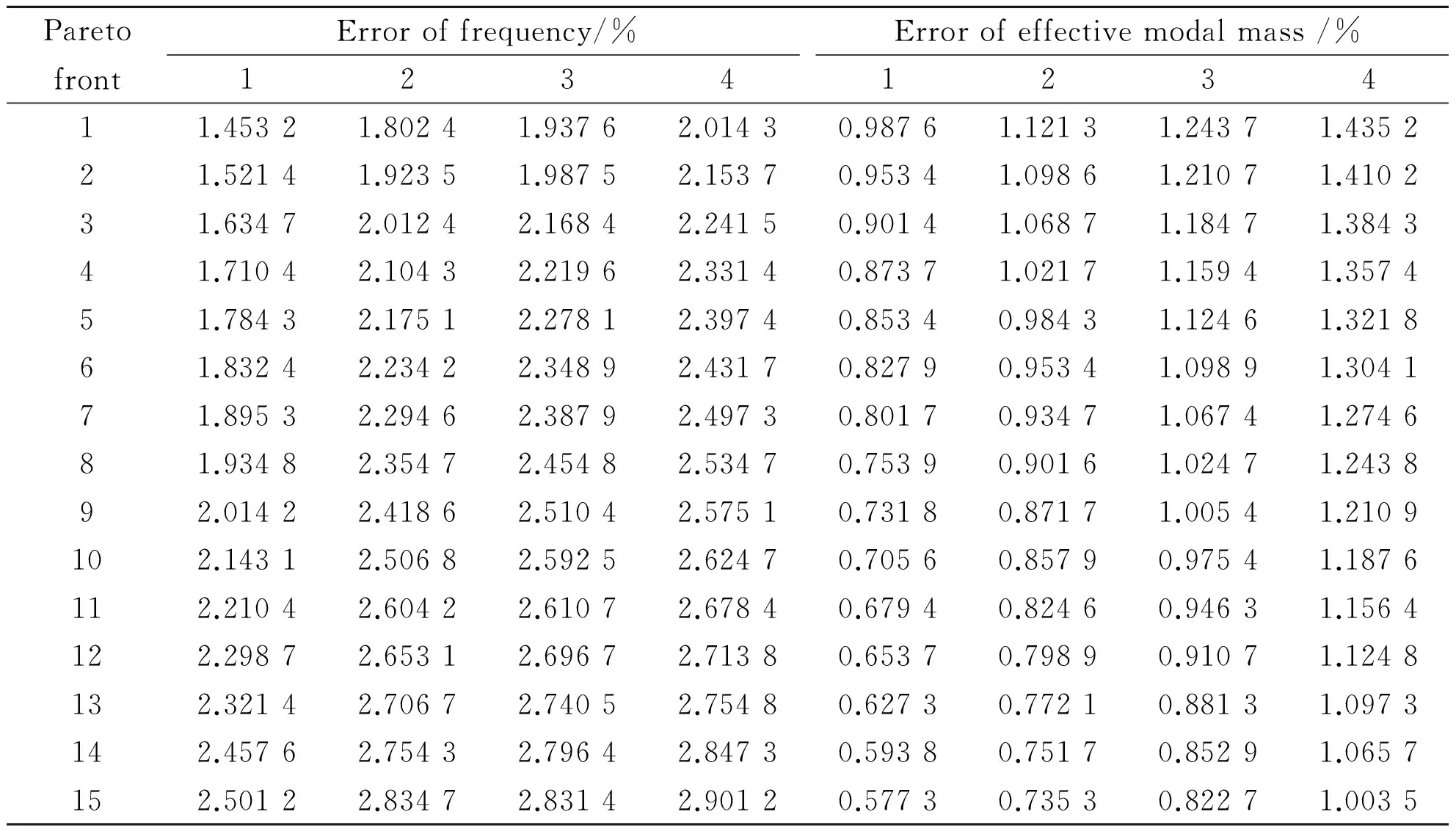
Table 6 Comparison between updated results and experiment values of Pareto frontier
4 Conclusions
An inverse approach for solving the model updating in HTE is presented. The following conclusions can be drawn:
(1) By employing the hierarchical method, we decompose the problem into temperature field updating and dynamic structural updating. To improve the efficiency and robustness of estimation, the proposed method is constructed from SVR and AWS by turning the estimation of physical properties into a multi-objective optimization problem, with an approach of constructing the objective function, which combines the residues of modal frequency and effective modal mass. The method is verified by an FE model of the reentry vehicle with respect to the effect of temperature change.
(2) The developed method based on multi-objective optimization can improve the stability which influenced by the error of SVR.
(3) The estimation algorithm is proposed based on the thermal analysis module of MSC.Nastran code thus can be applied to estimate the physical properties of complex structures for model updating.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 11472132), the Fundamental Research Funds for Central University (No.NJ20160050), and the Fundamental Research Funds for Central University (No.NJ2016098).
[1]STEENACKERS G, GUILLAUME P. Finite element model updating taking into account the uncertainty on the modal parameters estimates[J]. Journal of Sound and Vibration, 2006, 296(4):919-934.
[2]THONON C, GOLINVAL J C. Results obtained by minimizing natural frequency and MAC-value errors of a beam model[J]. Mechanical Systems and Signal Processing, 2003, 17(1):65-72.
[3]MYERS R H, MONTGOMERY D C. Response surface methodology; process and product optimisation using designed experiments[M]. New York, USA: John Wiley and Sons, 2002.
[4]HE Cheng, HE Huan, CHEN Guoping. Multiobjective optimization of thin-walled structures for crashworthiness based on the global approximate function[J]. Journal of Nanjing University of Aeronautics and Astronautics,2012,44(4):472-477.(in Chinese)
[5]HAYKIN S. Neural networks: A comprehensive foundation[M]. First Ed. Upper Saddle River, NJ, USA: Prentice Hall PTR, 1994.
[6]HE W, WANG Z, JIANG H. Model optimizing and feature selecting for support vector regression in time series forecasting[J]. Neuro Computing, 2008, 72:600-611.
[7]TEUGHELS A, DE ROECK G. Damage detection and parameter identification by finite element model updating[J]. Archives of Computational Methods in Engineering, 2005, 12(2):123-164.
[8]NOWINSKI J L. Theory of thermoelasticity with applications[M]. The Netherlands: Sijthoff and Noordhoff, 1978.
[9]HE Cheng, CHEN Guoping, HE Huan, et al. Model updating of a dynamic system in a high-temperature environment based on a hierarchical method[J]. Finite Elements in Analysis and Design, 2013, 77:59-68.
[10]KHODAPARAST H H, MOTTERSHEAD J E, BADCOCK K J. Interval model updating with irreducible uncertainty using the Kriging predictor[J]. Mechanical Systems and Signal Processing, 2011, 25:1204-1226.
[11]HAAG T, HERRMANN J, HANSS M. Identification procedure for epistemic uncertainties using inverse fuzzy arithmetic[J]. Mechanical Systems and Signal Processing, 2010, 24(7): 2021-2034.
[12]BERTHELON T, CAPITAINE A. Improvements for interpretation of structural dynamics calculation using effective parameters for substructures[C]// Proc Int Conf Spacecrafi Structures and Mechanical Testing. Noordwijk, The Netherlands, ESA SP-321, 1991: 63-68.
[13]HARALAMPIDIS Y, PAPADIMITRIOU C, PAVLIDOU M. Multi-objective framework for structural model identification[J]. Earthquake Engrg. Struct. Yn, 2005, 34 (6):665-685.
[14]KIM I Y,WECK DE O L. Adaptive weighted-sum method for bi-objective optimization: Pareto front generation[J]. Struct Multidisc Optim, 2005, 29: 149-158.
[15]VAPNIK V. Statistical learning theory[M]. New York: John Wiley and Sons, 1998.
[16]VAPNIK V. The nature of statistical learning theory[M]. New York: Springer-Verlag, 1995.
Dr. He Huan is an associate professor in Nanjing University of Aeronautics and Astronautics (NUAA). He received his first degree and Ph.D. degree in NUAA. His research interests focus on computational structural dynamics.
Dr. He Cheng is a research assistant in NUAA. He received his Ph.D. degree in NUAA. His research interests focus on computational structural dynamics, emission and recovery for UAV.
Dr. Chen Guoping is a professor and doctoral supervisor in NUAA. He received his Ph.D. degree from NUAA. His research interests focus on structural dynamics.
(Executive Editor: Zhang Tong)
, E-mail address: hechengary@163.com.
How to cite this article: He Huan, He Cheng, Chen Guoping, et al. Model updating for high speed aircraft in thermal environment using adaptive weighted-sum methods[J]. Trans. Nanjing Univ. Aero. Astro., 2016,33(3):362-369.
http://dx.doi.org/10.16356/j.1005-1120.2016.03.362
TP391Document code:AArticle ID:1005-1120(2016)03-0362-08
杂志排行
Transactions of Nanjing University of Aeronautics and Astronautics的其它文章
- Behavior of Corrosion-Repaired Concrete Beams Reinforced by Epoxy Mortar
- Stiffness Distribution and Aeroelastic Performance Optimization of High-Aspect-Ratio Wings
- DNS Study on Volume Vorticity Increase inBoundary Layer Transition
- Numerical Calculations of Aerodynamic and Acoustic Characteristicsfor Scissor Tail-Rotor in Forward Flight
- Removing Random-Valued Impulse Noises by a Two-Staged Nonlinear Filtering Method
- Robust Fault-Tolerant Control for Longitudinal Dynamics of Aircraft with Input Saturation
