大跨钢桁梁斜拉桥施工期主梁气动系数数值识别
2016-09-06郑建新李鑫
郑建新,李鑫
大跨钢桁梁斜拉桥施工期主梁气动系数数值识别
郑建新,李鑫
(中交第二航务工程局有限公司,长大桥梁建设施工技术交通行业重点实验室,湖北武汉430014)
忠建河大桥为“V”形峡谷区双塔双索面钢桁梁斜拉桥。文中结合该工程,通过数值模拟研究其在施工状态下的主梁气动力系数。采用二维非定常雷诺平均(URANS)的计算流体动力学方法计算主梁绕流空气场,在此基础上对桁梁截面静风荷载系数和颤振导数进行识别,所得结果与已发表文献中具有类似几何形式主梁的数据进行对比验证。分析表明,URANS方法用于桁梁气动系数识别是切实可行的,建议工程计算采用。
钢桁梁;风荷载;CFD;气动系数;颤振
0 引言
钢桁加劲梁的气动系数是进行颤振分析计算的基本参数,就其获取手段而言有现场实测、风洞试验和数值模拟三种途径。现场实测仅针对已建成桥梁可行,工程中对桥梁气动系数的研究主要依靠风洞试验和数值模拟[1]。风洞试验是最传统最基本的研究方法,但研究周期较长,价格昂贵,近年来,越来越多的研究者开始尝试通过计算流体动力学(Computational Fluid Dynamics,CFD)方法进行数值模拟识别获得桥梁的气动系数[2-5]。然而,这些研究多局限于矩形柱体、流线型箱梁等具有简单几何外形构件的气动稳定性,对钢桁梁气动系数的CFD数值模拟研究则报道不多。
1 工程概况
忠建河大桥(ZJHB)为跨径布置(46+134+400+ 134+46)m的双塔双索面公路钢桁加劲梁斜拉桥,桥址处地形起伏较大,微地貌为“V”形峡谷。钢桁加劲主梁宽26 m,高6 m。桥梁总体布置见图1,钢桁梁标准断面见图2。
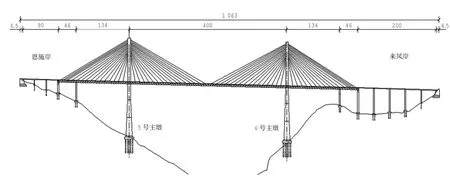
图1 桥梁总体布置图(单位:m)Fig.1 Overall layout of the bridge(m)

图2 钢桁梁标准断面图(单位:cm)Fig.2 Standard cross section of the steel truss(cm)
2 数值模型
流动计算采用非定常雷诺平均URANS方法,数值模拟在通用流体计算软件FLUENT平台上进行。数值计算域尺寸和边界条件如图3所示。
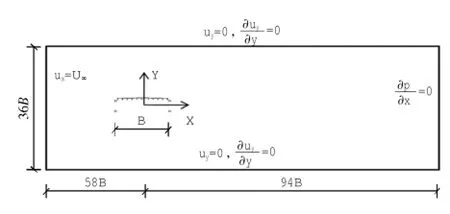
图3 数值计算域与边界条件Fig.3 Numerical computational domain and boundary conditions
计算域为矩形,左侧为速度入口边界条件,右侧为压力出口边界条件,上下为对称边界,截面边界为壁面。以主梁宽度为特征尺寸,计算域宽度为36B,断面距离上游入口58B,距离下游出口94B。为保证各工况计算雷诺数的一致性,计算来流风速保持为恒定常数。横型参数见表1。

图4 施工阶段主梁简化几何模型Fig.4 Simplified geometric model of main truss in construction
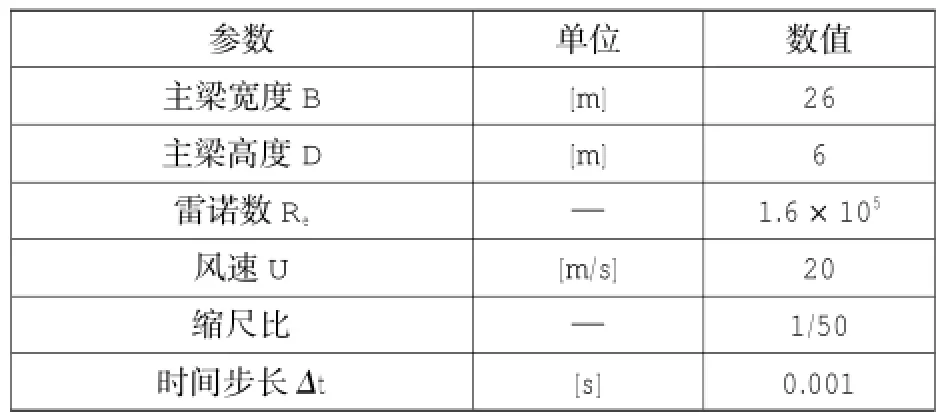
表1 数值计算模型参数Parameters of the computational model
出于研究目的,加劲主梁桁架忽略竖杆的影响,取余下全桥贯通的部分进行截面简化,见图4。图4中的两个典型截面分别选取了桁架节点处的主梁断面和两节点中间位置处的主梁断面,本文后面所讨论的主梁气动系数均是基于这两个典型断面计算结果所取的平均值。
网格划分采用混合网格方案,数值计算域被划分为两个部分,远离复杂几何外形的外围区域划分成结构画的四边形网格,而断面附近的区域划分的是非结构四边形网格,具体网格生成情况见图5,模型网格总数量约为240 000。数值模拟计算中,风攻角的变化通过旋转内部断面的几何位置多次重复建模实现,这与桥梁模型风洞试验时常用的攻角改变方式十分类似,计算中考查了-5°、-3°、-1°、0°、1°、3°和5°共7个风攻角条件下的主梁静力三分力系数。

图5 计算网格Fig.5 Calculate mesh
3 主梁静力三分力系数数值识别
平均风产生的静风荷载可以通过静力三分力系数描述:阻力系数CD=2FD/(ρU2D),升力系数CL=2FL/(ρU2B)和扭矩系数CM=2FM/(ρU2B2),其中:U为入口风速;ρ为空气密度;B为主梁宽度;D为主梁高度。
本文计算的三分力系数通过与矮寨大桥(AZB)的计算数据进行对比验证[6]。矮寨大桥与本文研究的桥梁截面较为类似,其横截面图如图6所示。
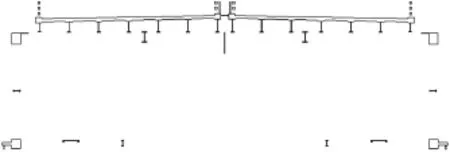
图6 矮寨大桥横截面简化图Fig.6 Simplified cross section of Aizhai Bridge
与本文研究情况不同的是,矮寨大桥研究的是成桥状态的横截面,在分析中考虑了附属结构的影响,其相关数据是使用LES模型研究得出。两者对比如图7所示。
从图7中可以看出,两座桥三分力系数具有相似的变化趋势,对本文数据的正确合理性提供了支持。
图7给出了使用RANS模型计算的忠建河大桥主梁三分力系数随风攻角的变化情况,从图中可以看出,扭矩系数数值接近于0,可以忽略,主梁不会有扭矩发散的危险。阻力系数在0攻角附近达到最小值,并且随风攻角变化平缓。升力系数的斜率为正,保证了不会发生主梁弛振。

图7 三分力系数对比Fig.7 Comparison of aerodynamic coefficients
4 主梁颤振导数数值识别
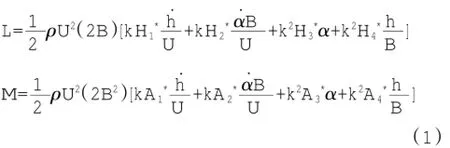
颤振导数的识别方法主要有两种:自由振动法和强迫振动法。自由振动法先让模型断面做自由振动,对其振动时程数据进行分析识别出颤振导数。强迫振动法则通过直接测定自激力,再直接推算颤振导数。自由振动法在风洞实验中易实施,但精度不高。强迫振动法具有更高的准确度和稳定性,但该方法需要复杂的设备和昂贵的费用。对于CFD方法而言,强迫振动法较之于自由振动法更方便,故本文采用强迫振动法。Scanlan建立的适用于桥梁主梁断面的颤振自激力表达式中,其气动升力L和气动力矩M如下:式中:k=bω/U为折减频率;ω=2πf为圆频率;f为强迫振动频率;h和h.为竖向位移及其对时间的导数;α和α.为扭转位移及其对时间的导数;B为桥横截面宽度;U为来流平均风速;定义U*= U/fb为无量纲折减风速;Hi*和Ai*(i=1,2,3,4)是颤振导数,其中H1*、H2*分别为由竖向运动与扭转运动引起的气动阻尼对自激升力的贡献,H3*、H4*分别为由扭转运动与竖向运动引起的气动阻尼对自激升力的综合贡献,A1*、A2*分别为由竖向运动与扭转运动引起的气动阻尼对自激扭矩的贡献,A3*、A4*分别为由扭转运动与竖向运动引起的气动惯性及气动刚度对自激扭矩的综合贡献。
图8为使用强迫振动法通过CFD模拟计算出的忠建河大桥的颤振导数,并给出矮寨大桥相应的颤振导数。通过两者的对比可以看出,两者的颤振导数随着风速的变化,有着相似的变化趋势,可作为对本文计算结果的一个验证。据此说明,URANS对于桁梁颤振导数的识别具有可行性。
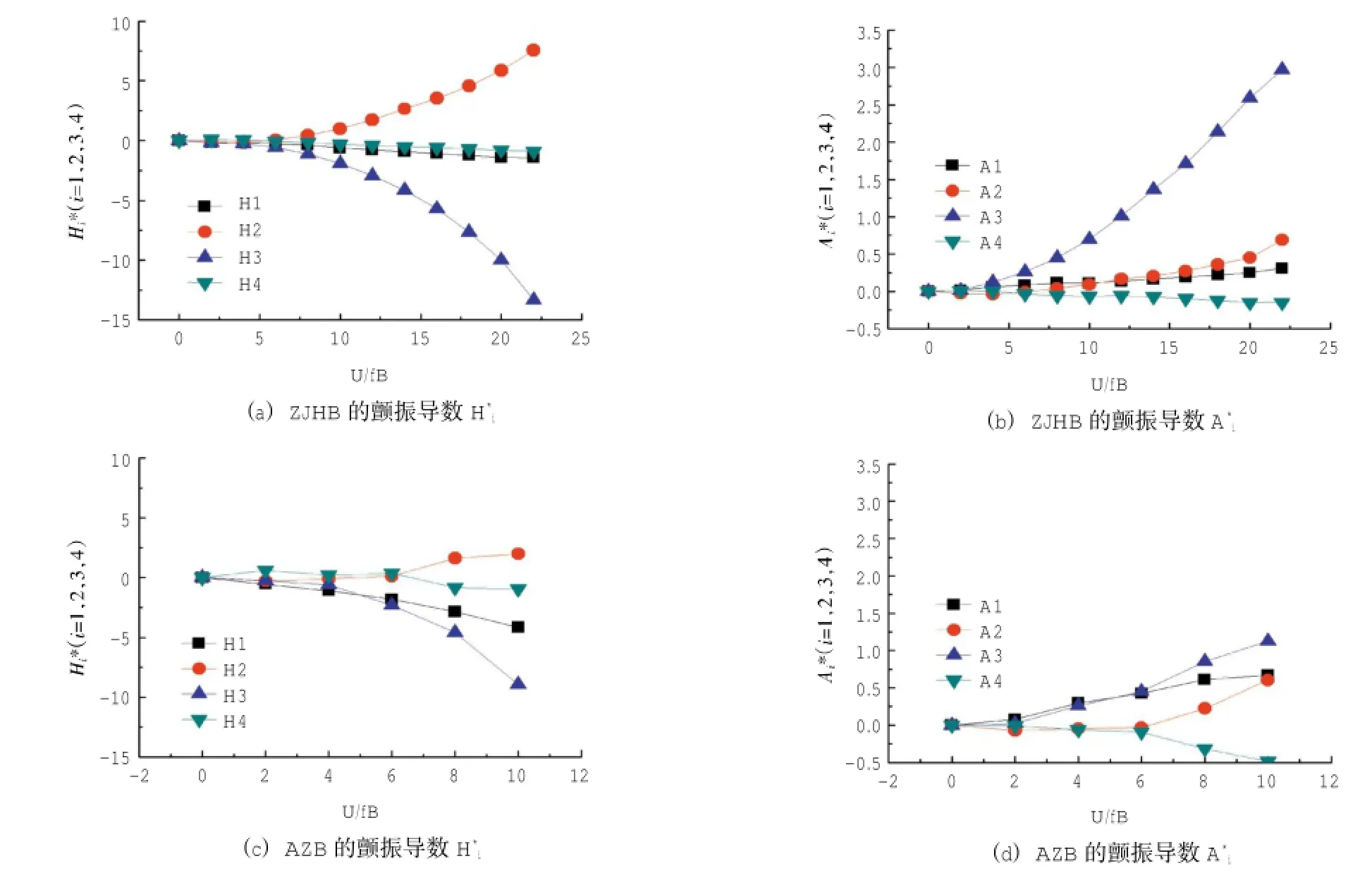
图8 颤振导数对比Fig.8 Comparison of flutter derivatives
5 结语
本文研究了忠建河大桥施工期间的气动参数,结果的合理性通过与文献中具有类似截面的桥梁进行对比验证,结果显示,两者的三分力系数和颤振导数的变化趋势均有相似性。研究表明,URANS方法对于桁梁气动导数的识别是可行的,可以推荐应用到工程计算中。
[1]项海帆.进入21世纪的桥梁风工程研究[J].同济大学学报,2002,30(5):529-532. Xiang Hai-fan.Study on bridgewind engineering into 21stCentury [J].Journalof TongjiUniversity,2002,30(5):529-532.
[2]SHIMADA K,ISHIHARA T,WAKAHARA T.Prediction of flutter characteristicsof rectangular cross-sections by k-εmodel[C]//The second international symposium on advances in wind and structures.Busan,Korea.2002:291-296.
[3]LARSEN A.Computation of aerodynamic derivatives by various CFD techniques[C]//The fourth international symposium on computationalwind engineering.Yokohama,Japan.2006:287-290.
[4]LARSEN A,WALTHER J.Discrete vortex simulation of flow around five generic bridge deck sections[J].W ind Eng.Ind. Aerodyn,1998(98):591-602.
[5]SUN D,OWEN J S,WRIGHT N G.Application of the k-ε turbulencemodel for a wind-induced vibration study of 2D bluff bodies[J].Wind Eng.Ind.Aerodyn,2009(97):77-87.
[6]陈艾荣,艾辉林.计算桥梁空气动力学—大涡模拟[M].北京:人民交通出版社,2010. CHEN Ai-rong,AIHui-lin.Calculation of bridge aerodynamics: large eddy simulation[M].Beijing:China Communications Press,2010.
Numerical identification of aerodynamic characteristics of long-span truss girder bridge under construction
ZHENG Jian-xin,LIXin
(CCCCSecond HarborEngineering Co.,Ltd.,Key Lab of Large-span Bridge Construction Technology, Ministry of Communication,Wuhan,Hubei430014,China)
Zhongjianhe Bridge is located in"V"shaped canyon area,its form is double tower cable-stayed steel trussgirder. Combined with the project,we studied the aerodynamic characteristics of themain girder bridge during construction through numerical simulation.The flow around a truss bridge is simulated by two-dimensional(2D)unsteady Reynolds-averaged Navier-stokes(URANS)approach.Aerodynamic coefficients of wind loads acting on the truss girder section and flutter derivatives are investigated.The results are compared with published data of another famous bridge with similar cross section. The results show that the URANSmethod is adequate to identify the truss girder aerodynamic characteristics,and proposed in engineering calculation.
truss girder;wind loads;CFD;aerodynamic coefficients;flutter
U441.3
A
2095-7874(2016)04-0047-04
10.7640/zggw js201604012
2015-10-22
2016-01-04
郑建新(1982—),男,湖北红安人,硕士,工程师,桥梁与隧道工程专业,从事桥梁结构分析与施工监控。E-mail:173240029@qq.com
