带乘性噪声附等式约束的非线性系统滤波算法*

王昌盛，张　玲，臧爱云，王　琨

(中国海洋大学工程学院，山东省高校海洋机电装备与仪器重点实验室 山东 青岛 266100)



带乘性噪声附等式约束的非线性系统滤波算法*

王昌盛，张玲，臧爱云，王琨

(中国海洋大学工程学院，山东省高校海洋机电装备与仪器重点实验室 山东 青岛 266100)

随着控制理论与计算机的飞速发展，非线性滤波已在各领域得到广泛应用。本文针对一类带乘性噪声附等式约束非线性系统，提出了一种状态滤波算法。该算法首先将状态方程和观测方程分别通过泰勒公式展开，得到新的带乘性噪声附等式约束的线性系统模型，然后通过最优观测的方法将观测方程扩维，再基于投影定理进行求解得到滤波算法，最后通过仿真验证了算法的有效性。

乘性噪声； 等式约束； 非线性滤波;投影定理； 最优观测

引用格式：王昌盛， 张玲， 臧爱云. 带乘性噪声附等式约束的非线性系统滤波算法[J].中国海洋大学学报(自然科学版), 2016, 46(8): 137-140.

WANG Chang-Sheng，ZHANG Ling，Zang Ai-Yun. Filtering algorithm for nonlinear systems with equation state constraints and multiplicative noise[J].Periodical of Ocean University of China, 2016, 46(8): 137-140.

随着控制理论与计算机技术的飞速发展，非线性滤波已在通信与信号处理、航空航天、导航定位等众多领域得到了越来越广泛的应用，观测手段的丰富使得对于物理特征及现象有了更深入的了解，从而得到更多的先验信息，建立约束，结合非线性滤波，可以提高滤波精度。

国内外的众多学者针对带有约束条件的非线性系统滤波做了大量的研究工作。Simon J等人系统地阐述了非线性等式约束的卡尔曼滤波算法[1]，KandePu等人和Brunoo等人研究了等式约束无迹卡尔曼滤波算法[2]，Simon D概述了状态约束的卡尔曼滤波的线性和非线性算法[3]，X Fu等人利用卡尔曼滤波对于线性和非线性混合约束下的系统进行滤波[4],Linfeng Xu等人在对于约束不是严格要求的条件下，提出了卡尔曼滤波的线性和非线性算法[5],刘杰将等式约束转化成凸二次规划，给出了约束滤波估计值的显式表达式[6]。

尽管对带等式约束的非线性系统滤波的研究进行了深入研究，但其算法大都建立在一般状态空间模型，而在实际系统中，往往还存在着乘性噪声，而带乘性噪声系统在非线性系统[7]、水声通信[8]、故障检测[9]、卫星姿态估计[10]等领域有了广泛的应用。

本文针对带乘性噪声附等式约束的非线性系统的滤波算法进行了研究。通过泰勒展开、状态扩维等方法以及投影定理得到了带乘性噪声附等式约束非线性系统的滤波算法。

1　模型描述

1.1 非线性模型

对于带乘性噪声非线性系统，其状态空间模型为：

xk=f(xk-1)+wk，

(1)

zk=mkh(xk)+vk。

(2)

其中：xk∈Rm为状态向量；zk∈Rn为量测向量；wk∈Rr为系统噪声；vk∈Rn为量测噪声；mk为一维乘性噪声，f()、h()分别是m、n维非线性向量函数。设系统满足以下条件：

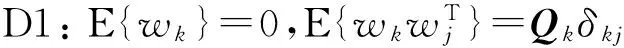
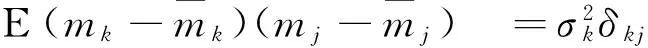
D5：随机序列{mk},{wk},{vk}及初始状态x0彼此相互统计独立。

假定系统(1)(2)有如下状态约束：

Dkxk=dk。

(3)

其中：Dk是s×m阶常量矩阵；dk是s×1阶常向量。s是状态约束量。并且s≤m。本文假设Dk是满秩矩阵，且秩为s阶。

1.2线性模型

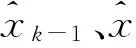
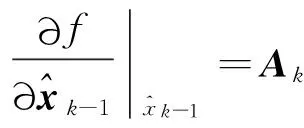
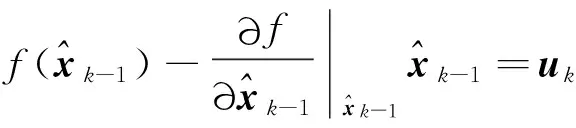
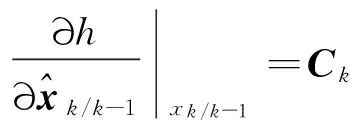
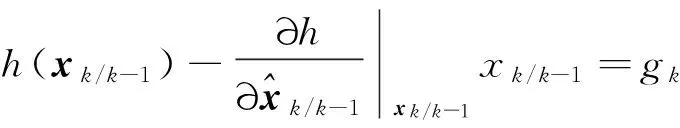
则原系统的近似状态空间表达：

xk=Akxk-1+uk+wk，

(4)

zk=mkCkxk+mkgk+vk。

(5)

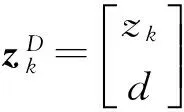
xk=Akxk-1+uk+wk，

(6)

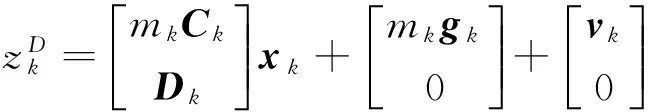
(7)

2　算法推导

针对(6)、(7)带乘性噪声附等式约束的系统，有如下定理：

定理对于式(6)、(7)的系统满足假设条件，则有如下的状态滤波递推算法：

状态滤波估计

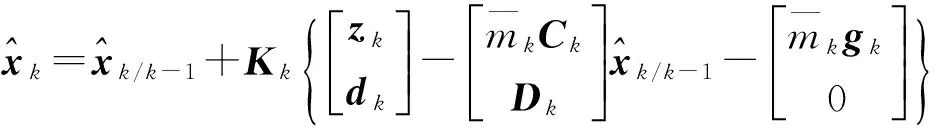
(8)

状态一步预测

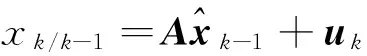
(9)

增益矩阵

(10)

输出残差方差阵

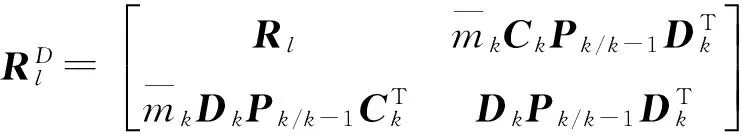
(11)

其中

(12)

状态相关矩阵

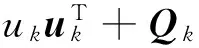
(13)

状态均值

jk=E[xk]=Ajk-1+uk-1。

(14)

一步预测误差方差阵

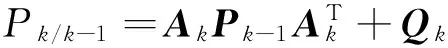
(15)

误差方差阵

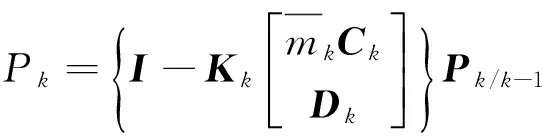
(16)

初值：

x0/0=E(x(0))。

(17)

P0=S(0)。

(18)

证明针对(4)、(5)，由投影定理得，

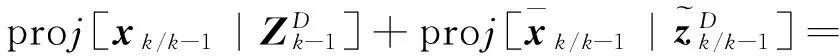
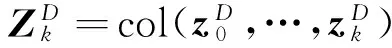
状态一步预测为

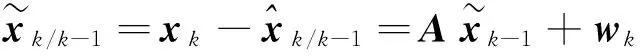
由假设条件及投影定理公式，有观测一步预测为

而输出残差为

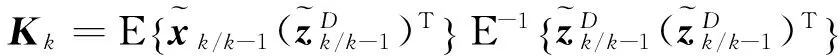
其中

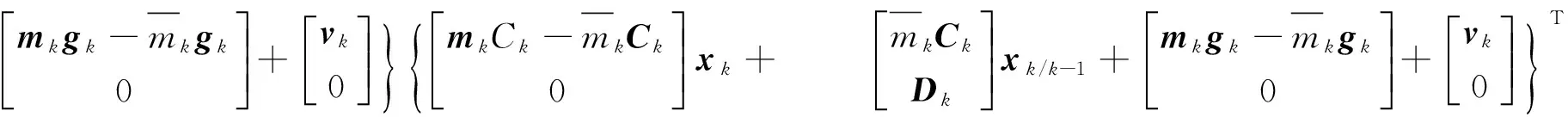
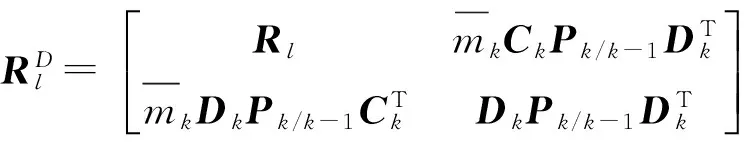
其中

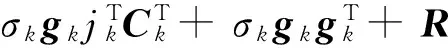
其中

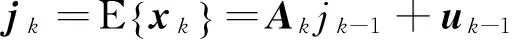
可得一步预测误差方差阵

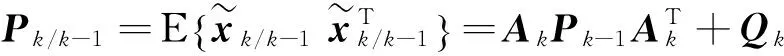
滤波误差

误差方差阵

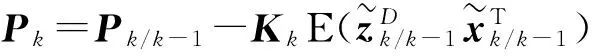
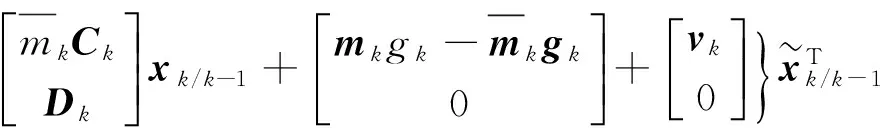
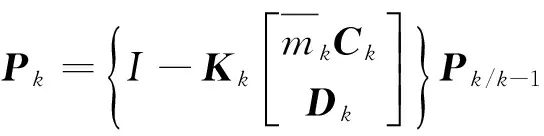
至此，算法推导完毕。

3　算法仿真

假设一辆行驶中的汽车，状态x的前两个状态分量是地面车辆的北坐标和东坐标，后两个状态分量由北方向速度和东方向速度表示。给出系统的运动模型：

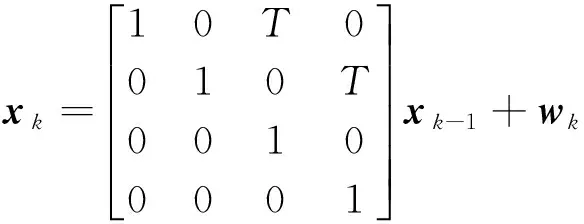
用一个参考点来确定其行驶路线，即(x0,y0)，取为(100,100)，其中每个参考点都是通过汽车的北方向与东方向位置来定的，在运动期间不可避免的存在抖动振动的影响，为了更客观的描述测量模型的随机干扰，还要考虑乘性噪声，则系统的观测模型为：

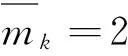
Dkxk=dk，其中

利用Matlab对本文的算法进行仿真，历元总数为100s，北方向跟踪效果如图所示。

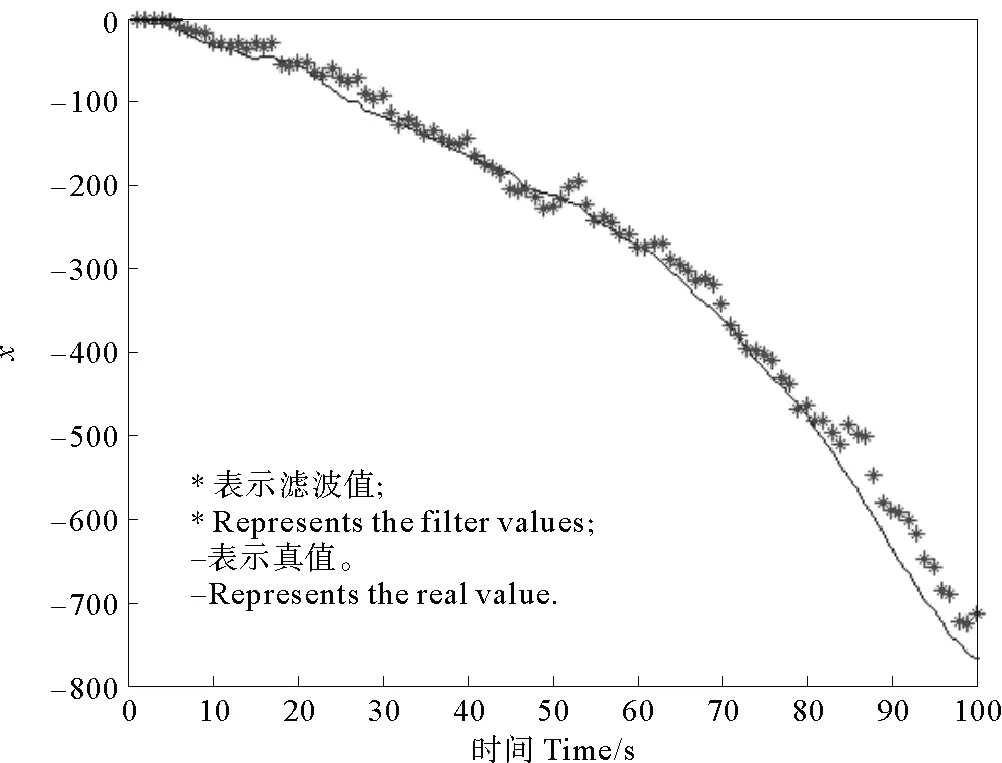
图1　北方向的真值和滤波值

图1给出了状态第一分量,既北方向的滤波结果。图中示出了状态第一分量的真值和滤波值，从整体趋势上来看，跟踪效果明显，验证了算法的有效性。

图2为状态第一分量真值和滤波值的相对误差值，滤波相对误差平稳，但一直存在，但这是由于将系统模型线性化时，去掉了泰勒展开的高阶项后，模型的不精确造成的，同时由于带乘性噪声系统结构的复杂性，这个问题涉及到线性模型转化的方面，是以后要继续研究的方向。

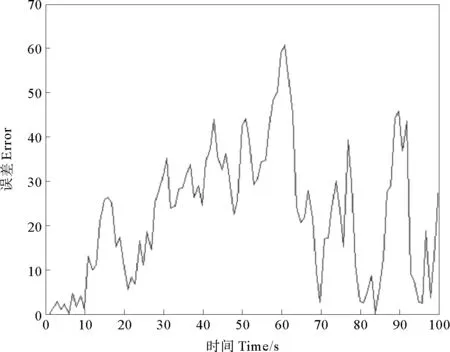
图2　北方向的真值和滤波值相对误差

4　结语

针对等乘性噪声附等式约束的非线性系统的状态滤波问题，该算法通过泰勒公式将系统的状态方程和观测方程展开，得到线性系统，利用观测最优的方法对观测方程进行扩维，最后利用投影定理对变形后的系统进行滤波求解。仿真结果验证了本文算法的有效性。

本文的算法也存在着不足，只考虑了扩展卡尔曼滤波的方法，还没有分析线性化对于误差的影响，同时关于非线性系统的滤波方法还有其他方法没有考虑。

[1]Julier S J， LaViola J J J L. On Kalman filtering with nonlinear equality constraints [J]. IEEE Transactions on Signal Processing, 2007,55(6): 2774-2784.

[2]Kandepu R, Imsland L, Foss B. Constrained state estimation using the unscented Kalman filter[C]. Ajaccio, France: 16th Mediterranean Conference on Control and Automation, 2008: 1453-1458

[3]Simon D. Kalman filtering with state constraints: A survey of linear and nonlinear algorithm[J]. IET Control Theory and Applications, 2010, 4(8): 1303-1318.

[4]Fu X, Jia Y, Du J, et al. Kalman Filtering with Multiple onlinear-linear Mixing State[C]. 49th IEEE Conference on Decision and Control ecember 15-17, 2010 Hilton Atlanta Atlanta, GA, Hotel, USA: 340-345.

[5]Xu Linfeng, Rong X, Li F, et al. Modeling and state estimation for dynamic systems with linear equality constraints[J]. IEEE Transactions on Signal Processing， 2013, 61(11): 2927-2939.

[6]刘杰. 附等式约束的卡尔曼滤波算法研究与应用[D]. 长沙： 中南大学， 2011.

Liu J. A study of Kalman Filtering Algorithm with Equality Constraints and Its Application [D]. Changsha: Central South University, 2011.

[7]褚东升, 张征. 一类带乘性噪声非线性系统的估计算法研究[D]. 青岛： 中国海洋大学， 2006.

Chu D S, Zhang Z. Study of Estimation Algorithm for a Class of Nonlinear Systems with Multiplicative Noise [D]. Qingdao: Ocean University of Qingdao, 2006.

[8]褚东升, 尹正飞, 张玲. 基于带乘性噪声模型的水声通信字符估计算法研究[J].中国海洋大学学报(自然科学版)， 2012， 42(1-2)： 149-152.

Chu D S, Yin Z F, Zhang L. Study of symbol estimation algorithm for underwater acoustic communications with multiplicative noise model [J]. Periodical of Ocean University of China, 2012, 42(1-2):149-152.

[9]褚东升, 董琦, 张玲. 带乘性噪声系统的传感器故障检测方法[J].中国海洋大学学报(自然科学版), 2013, 43(4): 112-116.

Chu D S, Dong Q, Zhang L. Study of sensor fault detection method based on systems with multiplicative noise [J]. Periodical of Ocean University of China, 2013, 43(4): 112-116.

[10]王炯琦, 矫媛媛, 周海银, 潘晓刚. 适合处理乘性噪声估计卫星姿态的非线性迭代滤波算法[J]. 电子学报, 2011, 39(6)： 1417-1422.

Wang J Q, Jiao Y Y, Zhou Y H, Pan X G. An iterative filter for nonlinear satellite attitude determination system with multiplicative stochastic matrix [J]. Acta Electronica Sinica, 2011, 39(6): 1417-1422.

责任编辑陈呈超

Filtering Algorithm for Nonlinear Systems with Equation State Constraints and Multiplicative Noise

WANG Chang-Sheng， ZHANG Ling， ZANG Ai-Yun, WANG Kun

(College of Engineering, Ocean University of China, The Key Laboratory of Marine Mechanical and Electrical Equipment & Instruments of Shandong Provincial Universities, Qingdao 266100, China)

With the development of controlling theory and computers, the filtering for nonlinear systems has been widely used in some areas. This paper figures out a flitering algorithm for a kind of nonlinear system with equality state constraints and multiplicative noise. By changing the state equation and observation equations based on taylor formula, a new model of linear system with equation constraints and multiplicative noise can be obtained correspondingly. The dimension of the measurement equation is augmented by perfect measurements, and the filering algorithm is derived based on the projection throrem. At last, the simulation results show the effectiveness of the proposed algorithms.

multiplicative noise; equation state constraints; nonlinear filtering; projection theorem; perfect measurements

国家自然科学基金项目(51279185,41506114)；留学回国人员科研启动基金项目([2015]1098)；青岛市博士后研究人员应用研究项目资助

2014-11-12；

2015-06-10

王昌盛(1989-)，男，硕士生。主要研究方向：智能控制与智能信息处理。E-mail：wcswang@qq.com

TN929.3

A

1672-5174(2016)08-137-04

10.16441/j.cnki.hdxb.20140339

Supported by the National Natural Science Foundation of China(51279158,41506114),the Scientific Research Foundation for Returned Overseas([2015]1098), the Applied Research Projectfor Postdoctorof Qingdao.