AZ31镁合金温热变形本构方程
2016-09-05王忠堂
秦 博,王忠堂
(沈阳理工大学 材料科学与工程学院,沈阳 110159)
AZ31镁合金温热变形本构方程
秦博,王忠堂
(沈阳理工大学 材料科学与工程学院,沈阳 110159)
对AZ31镁合金进行温热拉伸实验,实验温度分别为20℃、100℃、150℃、200℃、250℃和300℃,应变速率分别为 0.001s-1、0.01s-1和0.1s-1,分析流动应力与真实应变的关系。采用Arrhenius方程,根据实验数据,建立了AZ31镁合金温热变形本构方程,计算出镁合金温热条件下变形激活能,建立的本构方程的计算结果与实验结果最大相对误差为15.5%。
AZ31镁合金;本构关系;流动应力;温热变形
镁合金作为最轻的金属材料之一,具有较高的比强度和比刚度、传热性能好、减震能力强,具有良好的电磁屏蔽性以及良好的切削、铸造、焊接性能,易回收、资源丰富等优点[1]。而AZ31镁合金作为一种商用镁合金,广泛适用于汽车、航天和电子通讯等多种领域来替代铁、铝等相对较重的金属,被誉为21世纪最具开发潜力和应用前景的金属材料[2-3]。
目前AZ31镁合金的温热变形过程中的本构关系方面研究并不是很多,主要研究集中在300℃以上的热变形方面[4-7]。Fereshteh-Saniee等[4]采用布里奇曼数值校正因子对AZ31、AZ80和AZ81镁合金建立了拉伸和压缩状态下的本构方程。王忠堂等[5]对AZ31镁合金热变形建立本构方程,并改进Arrhenius方程。Ji Hoon Kim等[6]分析了孪生、非孪生和滑移材料力学性能的影响。K.Piao等[7]通过模拟和设计装置分析了大应变情况下镁合金拉伸压缩试验尾部加工硬化的产生与消失情况。由于镁合金为密排六方晶体结构,滑移系较少,所以在低温下变形能力差,在一定程度上限制了镁合金的发展[5]。但随着各国学者的不断研究,努力开发温热条件下镁合金的变形能力,所以研究AZ31镁合金温热变形本构方程在为研究镁合金温热变形条件下的加工有重要的意义[8]。本文描述了AZ31镁合金真实应力与应变、应变速率以及温度之间的关系,为确定热变形工艺参数奠定基础。
1 应力-应变曲线
拉伸实验温度分别为室温、100℃、150℃、200℃、250℃和300℃,应变速率分别为 0.001s-1、0.01s-1和0.1s-1。拉伸试样沿着板材轧制方向截取,板材厚度为0.7mm,长度为127mm,宽度为34mm。
AZ31镁合金板材在不同应变速率和不同温度下的真实应力-应变曲线如图1所示。在实验所采用的三种应变速率条件下,温度较低的时候(从室温到200℃),镁合金板材在拉伸过程中表现出明显的加工硬化现象,温度较高的时候(从250℃到300℃),加工硬化现象不明显,而且在应变量很小的时候,回复和动态再结晶导致的软化即抵消了由于变形产生的硬化,这一现象可能与镁合金为密排六方结构有关,由于滑移系较少,当拉伸过程中容易达到稳定状态,进而产生加工硬化的现象[7-9]。

图1 AZ31镁合金板材单向拉伸实验结果
2 本构关系模型的建立


(1)
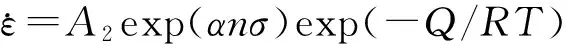
(2)
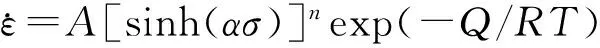
(3)

当温度不变时,Q、R、T和A均为常数,根据式(1)、(2)可以确定n、α值,分别为
(4)
(5)

图2 AZ31温热变形的关系曲线
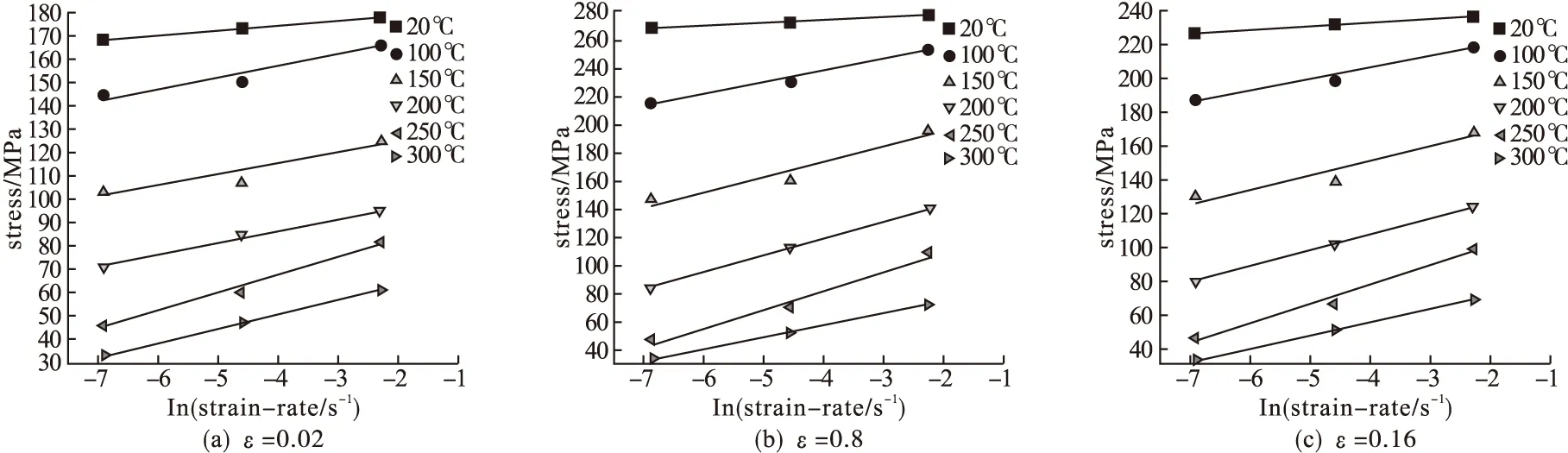
图3 AZ31合金的关系
当温度变化时,Q随着温度的变化而变化,此时R、α、n和A均为常数,由式(3)可以得到Q和lnA的计算式:
(6)
(7)
根据图1实验数据,绘制ln[sinh(ασ)]与1/T关系曲线,见图4。在不同的应变速率条件下,曲线趋势相同,曲线的斜率近似相等,即Q值基本不变,与应变速率无关。根据式(6),通过一元线性回归分析可求出各个应变下的Q值。将拟合出的n、α、Q值代入到式(7)中,即可求出lnA的值。

图4 AZ31镁合金的1/T-ln(sinh(ασ))的关系曲线
将拟合结果进行整理,温度为20~300℃,应变速率为0.001~0.1s-1的n、α、Q以及lnA值见表1。
对表1中的系数进行多项式线性回归拟合,得出材料特性参数与应变的关系式如下:
n=4858.0ε4-3746.4ε3+929.83ε2-73593ε+32.013
α=7.5421ε4-4.0592ε3+0.8653ε2-0.957ε+0.0099
Q=-4.3742×107ε4+1.2476×107ε3-2.2445×106ε2+9.6746×105ε+3.8245×105
A=exp(-33793.9ε4+13056.3ε3-2286.36ε2+447.537ε+104.685)

表1 本构关系模型参数的值
3 本构方程的验证
图5为AZ31镁合金温热变形本构方程的计算结果与实验数据的对比情况。误差分析结果表明,本构关系模型的计算值与实验值的最大相对误差为15.5%。本文所建立的AZ31镁合金温热变形本构关系模型能较好地描述AZ31温热变形在变形温度为20~300℃,应变速率为0.001~0.1s-1时的流动行为。
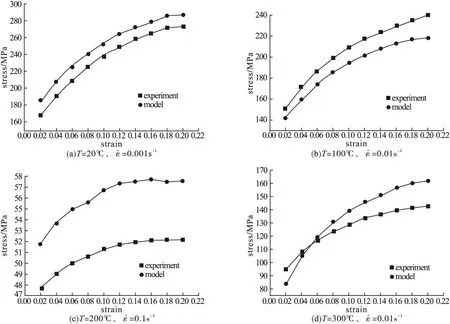
图5 AZ31镁合金本构关系模型的计算值与实验值的比较
4 结论
(1)本构关系模型的计算值与实验值的最大相对误差为15.5%,本构关系模型适用于变形温度为100~300℃,应变速率为0.001~0.1s-1时AZ31的流动行为。
(2)对本构方程的系数进行多项式线性回归拟合,得出材料特性参数与应变的关系式如下:
n=4858.0ε4-3746.4ε3+929.83ε2-73593ε+32.013
α=7.5421ε4-4.0592ε3+0.8653ε2-0.957ε+0.0099
Q=-4.3742×107ε4+1.2476×107ε3-2.2445×106ε2+9.6746×105ε+3.8245×105
A=exp(-33793.9ε4+13056.3ε3-2286.36ε2+447.537ε+104.685)
[1]左铁镛.21世纪的轻质结构材料——镁及镁合金发展[J].新材料产业,2007(12):22-26.
[2]刘庆.镁合金塑性变形机理研究进展[J].金属学报,2010,46(11):1458-1472.
[3]李宏战,李争显,杜继红,等.高强镁合金的研究现状[J].材料开发与应用,2011,26(6):89-92.
[4]F Fereshteh-Saniee,F Barati,H Badnava.An exponential material model for prediction of the flow curves of several AZ series magnesium alloys in tension and compression[J].Materials & design,2011(35):1-11.
[5]王忠堂,张士宏.AZ31镁合金热变形本构方程[J].中国有色金属学报,2008,18(11):179-183.
[6]Ji Hoon Kim,Daeyong Kim,Young-Seon Lee.A temperature-dependent elasto-plastic constitutive model for magnesium alloy AZ31 sheets[J].International Journal of Plasticity,2013,(50):66-93.
[7]K Piao,J K Lee,J H Kim.A sheet tension/compression test for elevated temperature[J].International Journal of Plasticity,2012(38):27-46.
[8]张士宏,王忠堂,周丽新,等.镁合金板材温热成形技术的几个新进展[J].材料导报,2006,20(8):114-118.
[9]郑文涛.镁合金AZ31板材温热冲压成形性能研究[D].沈阳:中科院金属研究所,2007:38-39.
[10]党淼.TAll本构关系及叶片微观组织模拟研究[D].沈阳:沈阳理工大学,2010:24-25.
[11]Sellars C M,Mctegar W J.On the mechanism of hot deformation[J].ACTA Metallurgica,1966(14):1136-1138.
(责任编辑:马金发)
Constitutive Equation of Warm Deformation of AZ31 Magnesium Alloy
QIN Bo,WANG Zhongtang
(Shenyang Ligong University,Shenyang 110159,China)
Warm tensile experiment of AZ31 Mg alloy had been finished at the temperature of 20℃,100℃,150℃,200℃,250℃ and 300℃ respectively,and strain rate 0.001s-1,0.01s-1and 0.1s-1.The relation of the true stress and true strain of magnesium alloy hadbeens analyzed.The constitutive equation was established based on the experimental data and Arrhenius equation.The deformation activation energy of magnesium alloy under the warm conditions was calculated.The maximum relative error between results of constitutive equation and that of experiment is 15.5%.
AZ31 magnesium alloy;constitutive relation;flow stress;warm deformation
2015-02-01
国家自然科学基金资助项目(51575366)
秦博(1989—),男,硕士研究生;通讯作者:王忠堂(1962—),男,教授,博士,研究方向:先进塑性加工技术。
TG146.22
A
