福田红树林自然保护区一体化动态监测模型
2016-09-05张伟科
张伟科
(沈阳理工大学 理学院,沈阳 110159)
福田红树林自然保护区一体化动态监测模型
张伟科
(沈阳理工大学 理学院,沈阳 110159)
深圳福田红树林自然保护区,由于其容积小,生态健康更加脆弱,迫切需要更加完善的监测系统、健康评估和预警系统。构建的一体化模型包含EWE模型、健康评价模型和动态预警模型三部分。其中EWE模型能快速反映生态系统特征,营养状况和关系;健康评价模型采用压力-状态-响应(PSR)模型,运用AHP层次分析法确定各层指标的权重系数,建立了湿地生态系统健康评价体系;预警模型采用多元线性回归分析法和灰色预测法对未来三年湿地生态系统的健康情况进行预测。根据数据计算出湿地生态系统评价值为0.519,属于亚健康状态。通过四种因素未来三年的预测值,可大致看出是什么因素导致生态系统的健康情况恶化,进而有针对性地对此项因素进行治理。
EWE模型;PSR模型;AHP层次分析法;灰色预测
深圳福田红树林自然保护区是我国最小的红树林保护区,面积仅有3.68平方公里,也是在城市的中心中国唯一的国家级自然保护区。
在深圳经济发展的30年时间里,城市扩张和环境污染使福田红树林湿地生态系统破坏较为严重,红树林湿地面积缩小,滩淤积导致海床上升,摩天大楼阻止候鸟的通道,水体污染导致鱼虾死亡,外来物种海桑已经对环境构成了侵犯,导致频繁爆发虫害使红树植物不能自然繁殖,生态问题日益突出,整个生态系统和空间结构生态过程,自我调节和更新能力,恢复能力等方面,都表现出不稳定和不可持续的迹象[1-2]。
1 动态监测模型整体构建思路
湿地生态系统动态监测模型是一个随着时间的推移动态采集数据,对采集后的数据处理分析,通过健康评估来给出生态系统的健康程度[3-5]。动态监测模型由三个子模型构成,模型之间的关系如图1所示。

图1 模型之间的关系
1.1生态系统EWE模型
生态系统(EWE)模型是基于动力学原理来直接建设生态系统的结构,其描述了能量转移的内部动态模式。最早是由Polovina提出,后来在Ulanowiez和奥德姆等人的研究成果基础上开发一个软件系统,EWE模型是分析物质流和系统组之间的生态系统功能的稳定性和成熟性,主要在不列颠哥伦比亚省渔业中心和国际水生生物资源管理中心等科研机构推广。EWE模型是在特定的时间内一种生态系统的快照(Snapshot),并能快速反映生态系统特征,营养状况和关系。
1.1.1模型原理
EWE生态系统模型由许多相互关联的官能团组成,官能团包括浮游生物,有机碎片,一些渔类,渔类的年龄组,植物或植物的年龄组等等,每个官能团能够覆盖能量转移的生态系统的全过程。在建模过程中生态系统功能组假设是相对稳定的,就是生态系统的总产出和总投入相等。公式如下:
Q=P+R+U
式中:Q代表消耗量;P代表生产量;R代表呼吸量;U代表未消化的食物量。根据热力学理论,EWE模型定义了各功能组的能量输出和输入保持不变。用数学公式来定义的生态系统如下:
Pi=Yi+M2i+Ei+BAi+Pi(1-EEi)
式中:Pi代表功能组i的总生产率;Yi代表功能组i的总捕捞率;M2i代表功能组i的总被捕食死亡率;Ei代表功能组i的净迁移率(包括迁出率,迁入率);BAi代表功能组i的生物量累积率;EEi代表功能组i的生态营养转化效率;MOi=Pi(1-EEi)代表功能组i的其它死亡率。
通过以上线性方程组来定量各种官能团的生态系统流和各官能团之间的相关能量生物参数。生物量进一步定量描述在食物网中流动,以及各种营养层次之间的相互作用的机理。
1.1.2功能组划分
根据有关生态学的理论对模型功能设置进行划分,生态特征(食物成分、摄食方式、个体尺寸、年龄构成等)类似进行合并以简化食物网[6]。
为了得到需要的数据,将福田红树林湿地生态系统划分为以下15个相关功能组,即:浮游动物、甲壳类动物、鸟类和碎片、软体动物、滩涂鱼类、多毛类、迁徙动物、浮游植物、桐花树、秋茄(6岁)、秋茄(20岁)、红树林、无瓣海桑、海桑。
1.1.3评价结果
福田红树林模型与其他类似的生态系统模型进行比较发现,福田红树林总生物量/总流量比巴西北部河口红树林系统低很多,比其他湿地生态系统低得多,这表明在福田红树林湿地生态系统,较少的其他生物资源,食物链联系松散,在相对简单的食物链结构失衡的情况下,该系统的自我修复能力差。
1.2健康评价模型
压力(Pressure)—状态(State)—反应(Response)模型(PSR)是国际通用的资源和环境评估模型,广泛应用于资源环境评估的各个领域,该模型有一个非常明确的因果关系,更科学地澄清人口、资源、环境三者之间关系,即人类对环境的活动施加了一定的压力;考虑到经济的高速发展造成的空气污染、光污染、水体污染等等问题,间接造成损害和破坏红树林生物多样性,其中最大的原因是人为因素,因此PSR模型的评价体系,非常适合深圳福田红树林湿地生态系统的早期预警系统[7]。
根据层次分析法的基本原理,综合红树林健康评价的实际情况和专家的意见,构建判断矩阵,计算出对应的特征根以及特征向量[8]。将各个指标特征根对应的特征向量值求出,作为该指标所对应的权重。通过计算出的最大特征根的值来判断矩阵的一致性。依此类推求出上一层各个元素的权重值,通过各个层次的权重乘积来求出单个指标对于总目标层的权重值。
根据层次分析法,按照红树林的实际情况和专家意见建立判断矩阵,计算出相应的特征根和特征向量。对应于所确定的特征根和特征向量,将特征根对应的特征向量求出。通过计算最大特征根的值来判断矩阵的一致性。依此类推求出上一层各个元素的权重值,通过各个层次的权重乘积来求出单个指标对于总目标层的权重值。
生态系统的健康评价值的计算公式:
(1)
式中:I是系统健康评价值;Wi是第i个指标的权重;Ii是第i个指标无量纲化后的值;n是指标项数。
将数据带入式(1),能够得出系统健康评价值,可以大致看出湿地生态系统的健康情况。
要更清楚地了解生态系统的健康情况,需要对照下面的湿地生态系统健康评价标准(见表1),此标准将健康情况分为“病态、不健康、亚健康、健康、很健康”五个级别。能合理地与系统健康评价值相协调,准确显示湿地生态系统的健康情况。

表1 湿地生态系统健康评价标准
1.3动态预警模型
动态预警模型主要是评估福田红树林生态系统的健康状况,采取积极有效的措施,防止环境退化,为生物多样性提供更好的生态服务。
可以通过对红树林生态系统长期连续的观测数据开展对森林生态系统服务功能的实物量与价值量评估[9]。
采用AHP层次分析法确定每个指标对生态系统健康估计值的权重系数,故将复杂的生态系统问题分解成四个相互联系、不同次序的层次,即目标层、准则层、因素层和指标层(见表2)。

表2 评价体系的层次结构
目标层:指标体系的最高层次,即生态系统的健康评价值。
准则层:分为压力子系统、状态子系统、响应子系统。是根据影响生态系统健康的方式划分。压力子系统是指影响湿地生态系统的作用力,分为人为和自然两种压力,直接造成湿地生态系统的兴盛或衰败。状态子系统是指表现湿地生态系统的当前状态的指标,湿地生态系统当前的状态可以由这些指标推测出来。响应子系统是指根据当前湿地生态系统的状态,人类所作出的响应,湿地生态系统未来的趋势由此系统限制。
因素层:即组成准则层的各个因素。
指标层:指标体系最基本的层次,根据因素层和指标选取原则进行筛选。
根据指标筛选的原则和对实际的考虑,构建了福田红树林湿地生态系统评价指标体系。
2 计算实例
要建立预警系统,就必须先知道未来湿地生态系统的健康情况或者发展趋势。在预警过程中,整体预测生态系统的健康评价值显然是没必要也是不可能的,故只选用生态系统的状态子系统的评价值来代表湿地生态系统的健康情况。而生态系统的状态可由保护区水质、保护区大气质量、植被覆盖率、大型底栖动物密度等四个因素来大致决定。
2.1健康评价的指标数据
2.1.1指标无量纲化
评价体系的指标多而杂,指标之间有着很大区别,比如具有不同的类型,不同的数量级。即存在着不可公度性,因此在使用数据之前需要做一定的预处理工作,以便可以带入评价公式。评级体系的指标大致可以分为以下两类:
1)极大型指标:指标数据越大,说明湿地生态系统越健康。其中有状态子系统的活力、组织、服务功能的全部指标和响应子系统的全部指标。
2)极小型指标:指标数据越小,说明湿地生态系统越健康。其中有压力子系统的全部指标和状态子系统的恢复力的全部指标。
在对指标数据处理之前,需找到一个参照标准值,因有的指标没有给出公认的参照值,所以以1989年深圳福田红树林生态环境受到较小干扰时的指标的数据作为参照指标数据。下面分别给出两种类型指标的无量纲化方法。
对于1)类指标的无量纲处理方法:
X无量纲化=X实际/X参照值
(2)
对于2)类指标的无量纲处理方法:
X无量纲化=X参照值/X实际
(3)
2.1.2权重的确定
本评价体系选用AHP层次分析法确定每个指标的权重系数。利用Matlab软件使用层次分析法程序计算出个各层权重。通过一致性检测后,输出结果即是该组的权重系数。如没通过一致性检测,则须重构建该组的判断矩阵。计算程序界面见图2。

图2 AHP计算程序界面
按照表2评价体系的层次结构模型,根据相关数据资料的分析,得出12组判断矩阵和权重系数如下:
(1)压力子系统、状态子系统、响应子系统的判断矩阵

(2)自然压力、人为压力的判断矩阵

(3)红树林病虫害次数、年极端温度、未来入侵物种数的判断矩阵

(4)周边生活,工业污水排放量、大气重度污染年天数率、噪音超过80dB的年天数率、人类土地利用强度、基围鱼塘面积的年均增长率的判断矩阵
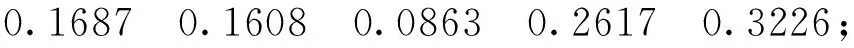
(5)活力、恢复力、组织、服务功能的判断矩阵

(6)植被覆盖率、叶绿素浓度的判断矩阵

(7)水体污染综合指数、土地污染综合指数的判断矩阵


(8)底栖动物均匀度、昆虫的多样性指数、浮游植物多样性指数、浮游动物多样性指数、红树林植物多样性指数、栖息鸟类多样性指数的判断矩阵

(9)濒危鸟类的多样性指数、候鸟多样性指数的判断矩阵

(10)系统功能响应、社会响应的判断矩阵


(11)湿地面积增多率的判断矩阵
[1]
1;
(12)污水治理率、环境污染治理投资额占总财政支出的比率的判断矩阵

最终计算结果见表3。
进一步通过对权重系数施行无量纲化后得到2014年福田红树林健康评价的指标数据如表4所示。

表3 评价体系各指标的权重系数
2.2多元线性回归模型
要预测未来生态系统的状态评价值,须找到状态评价值和保护区水质、保护区大气质量、植被覆盖率、大型底栖动物密度的关系。可以利用spss软件的多元线性回归分析功能完成。具体步骤如下:
(1)计算历年生态系统的状态评价值。
(2)将状态评价值与历年四种因素的数据输入到spss软件中。
(3)选择分析-回归-线性,将状态评价值选为因变量,其余五项选为自变量。
(4)在输出页,找到系数表格,系数一栏就是线性回归系数。
最终获得多元线性回归方程,即
I状态=∂1G1+∂2G2+∂3G3+∂4G4+β
(4)
式中:I状态是生态系统的状态评价值;Gi是保护区水质、保护区大气质量、植被覆盖率、大型底栖动物密度的无量纲化数据;∂i是保护区水质、保护区大气质量、植被覆盖率、大型底栖动物密度的线性回归系数;β是线性回归方程的常数项。

表4 2014年福田红树林健康评价的指标数据
2.2.1相关数据
从深圳福田历年年鉴中收集到所需要的数据。具体数据见表5和表6。

表5 福田红树林保护区历年健康状态评价值
2.2.2建立多元线性回归方程
根据相关数据,使用SPSS的多元线性回归分析功能,得出湿地生态系统状态健康值和保护区水质、大气质量、植被覆盖率、大型底栖动物密度的线性回归方程。即
I状态=0.212G1+0.058G2+5.248G3+0.012G4-0.813
(5)

表6 福田红树林保护区历年数据
2.2.3检验多元线性回归方程
再将数据带入方程检验线性回归系数是否合适,得到表7。
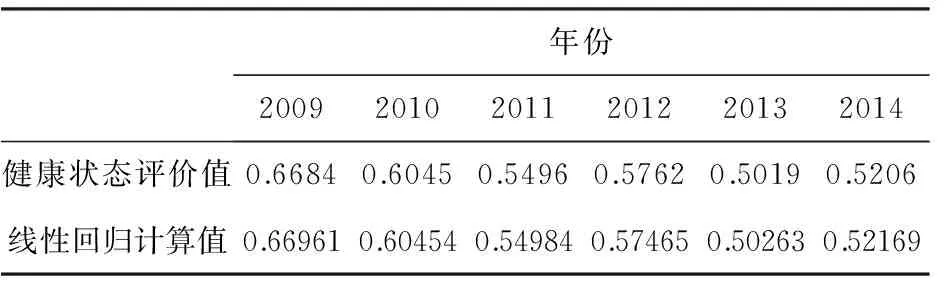
表7 健康状态评价值的真实值与预测值
通过表7的数据对比发现,预测值和真实值十分接近,说明线性回归方程对评价值和四种因素的关系拟合很好,线性回归系数可用。
2.3灰色预测
找到生态系统的状态评价值和保护区水质、保护区大气质量、植被覆盖率、大型底栖动物密度的关系后,需要通过预测这五个因素的值,来预测未来生态系统的状态评价值。
鉴于此刻能使用的数据较少,须预测的数据与时间有关,所以使用灰色预测方法对五个因素的数据进行预测。具体步骤如下:
1)做级比检验
以过去十年的某个因素的数据建立数据时间序列,即:
X(0)=(X(0)(1),X(0)(2),…,X(0)(10))
(6)
求级比λ(k):
(7)
根据级比公式(7)得出九个级比λ(k)。
若λ(k)∈(e-2/(n+1),e2/(n+1))即λ(k)∈(0.8338,1.1994),k=2,3,…,10;n=10。则数列可以作为模型GM(1,1)的数据进行灰色预测。
2)GM(1,1)建模
对原始数X(0)据作一次累加生成数列:
(8)
均值数列为
(9)
建立灰微分方程为
X(0)(k)+aZ(1)(k)=b
(10)
对灰微分方程白化:
(11)

(12)
由矩阵方程得
(13)
由最小二乘法得
u=(,
(14)
求解得
(15)
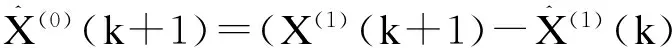
(16)
3)检验预测值
(1)残差检验
计算残差:
(17)
如果ε(k)<0.2,则可认为达到一般要求;如果ε(k)<0.1,则认为达到较高要求。
(2)级比偏差值检验
用发展系数求出相应的级比偏差:
(18)
如果θ(k)<0.2,则可认为达到一般要求;如果θ(k)<0.1,则认为达到较高要求。
2.3.1预测四种因素的值
利用灰色预测算法和收集到数据,使用Matlab软件预测未来三年保护区水质、大气质量、植被覆盖率、大型底栖动物密度四种因素的值见表8。计算程序界面如图3所示。

图3 灰度预测计算程序界面

表8 未来三年四种因素的预测值
四种因素的灰度预测模型的计算残差分别为:保护区水质=0.1691,大气质量=0.0172,植被覆盖率=0.0293,大型底栖动物密度=0.2963。
2.3.2状态评价值的预测
将预测到的数据带入到回归线性方程中得到未来三年的湿地生态系统的状态评价值。具体数据见表9。

表9 状态评价值的预测值
2.3.3状态评价值的分析
从保护区水质的预测值可以看出,保护区水体污染会越来越严重,如果不人工干预治理,保护区水质极有可能跌到Ⅲ类水的水平。状态评价值也是一直在下降,因为保护区水质、大气质量、植被覆盖率、大型底栖动物密度四项因素的值都在下降,即福田红树林湿地生态系统的健康情况在全面下降。对于现在这种情况,应该对湿地生态系统的健康情况发出预警,提示管理人员对治理方案做出调整或加强管理力度。
2.4生态健康评估和早期预警
预测出未来三年生态系统的四种因素的数据后,带入多元线性回归方程得到未来三年生态系统的状况评价值,通过同前十年的状况评价值比较和观察未来三年生态系统的状况评价值的趋势,若比前十年的状况评价值相差甚远,或者未来三年间状况评价值一直降低,则对生态系统的健康情况发出预警。通过四种因素未来三年的预测值,可大致看出是什么因素导致生态系统的健康情况恶化。进而有针对性的对此项因素进行治理。
针对不同因素,给出如下建议:
针对水质:
①加强污水治理强度,增加红树林生态水与深圳湾海水的交换;②对福田红树林内的水污染源分别进行截流,修建生态工艺的污水处理系统,采用污水集中处理;③处理后的水填充到基围鱼塘,调节鱼塘的水位和水质;④降低河道护岸标高,加强河口水体交换能力,利用潮汐能与上下游水位的落差,冲刷干流内淤积的泥沙。
针对植被,进行植被修复。可以通过以下几种方式来实现:植物萃取、植物挥发、根系过滤、植物钝化、植物降解。
针对大气,要提高湿地系统的氮沉降量,其值的降低对福田红树林的退化有很大的影响,与人类活动,降水强度及频次,风向都有关,要保持对其的动态监测,并控制对其影响较大的因素。
3 结束语
采用评价模型和预警模型联立的方法构建生态系统一体化模型。其中评价模型采用PSR模型,多方面、全方位考虑影响生态系统健康水平的因素,建立了全面、完整、科学的生态系统健康评价指标体系。
预警模型综合了多元线性回归分析算法和灰色预测算法,分析出生态系统状况评价值与四种因素的线性关系并建立其线性回归方程,然后预测四种因素在未来三年的趋势,准确预测出未来三年生态系统状况评价值。
[1]丛沛桐,于景华.东灵山辽东栋林植物生态场研究[J].植物研究,2001,21(1):147-151.
[2]王德利.植物生态场导论[M].长春:吉林科技出版社,1994.
[3]王根轩,赵松岭.半干早生态条件下植物个体的综合生态效应的空间距离分布规律[J].生态学报,1993,13(1):58-65.
[4]王德利,祝廷成.不同种群密度羊草生态场梯度及其变化特征[J].应用生态学报,1995,6(1):29-33.
[5]王根轩.生态场论[M].郑州:河南科学技术出版社,1993:78-79.
[6]罗忠奎,黄建辉,孙建新.红树林的生态学功能及其资源保护[J].亚热带资源与环境学报,2007(2):37-47.
[7]梁素娟,史秀华,张信文.福田红树林保护区土地类型的动态分析[J].林业资源管理,2009(4):74-78.
[8]何奋琳.深圳福田红树林生态系统生态恢复对策研究[J].环境科学与技术,2004(4):81-83.
[9]张丽珍,徐淑庆.广西北部湾红树林湿地生态功能的探讨[J].安徽农学通报(上半月刊),2010(23):134-136.
(责任编辑:马金发)
Integrated Dynamic Monitoring Model of Futian Mangrove Nature Reserve
ZHANG Weike
(Shenyang Ligong University,Shenyang 110159,China)
Due to small volume of Mangrove Nature Reserve and fragile ecological health,a dynamic monitoring wetland ecosystem health assessment and early warning systems is established urgently.Integrated model contains EWE Model,EWE Model can quickly reflect ecosystem characteristics,nutritional status and relationships.Health Evaluation Model uses pressure-state-response(PSR)model to establish a Wetland Ecosystem Health Assessment System and determine the weight of each layer index weight coefficient by using AHP Model.Dynamic Warning Model uses multiple linear regression analysis and gray prediction method to predict the next three years of the health of wetland ecosystems.According to the data the value of the wetland ecosystem evaluation is calculated,that is 0.519.It belongs to the sub-health state.By four factors and predicted value of the next three years,it can be seen roughly what factors led to the deterioration of the health of the ecosystem,targeting govern this factor.
EWE model;PSR model;AHP model;gray prediction method
2015-09-29
张伟科(1965—),男,讲师,研究方向:智能计算。
O157.5
A
