侧加热腔体内对流特性的研究

李开继，宁利中，宁碧波，田伟利

(1．西安理工大学 西北旱区生态水利工程国家重点实验室培育基地，陕西 西安 710048； 2．嘉兴学院 建筑工程学院，浙江 嘉兴 314001；3．上海大学 美术学院，上海 200444)



侧加热腔体内对流特性的研究

李开继1，宁利中1，宁碧波2，田伟利3

(1．西安理工大学 西北旱区生态水利工程国家重点实验室培育基地，陕西 西安 710048； 2．嘉兴学院 建筑工程学院，浙江 嘉兴 314001；3．上海大学 美术学院，上海 200444)

本文通过二维流体力学方程组数值模拟，研究了侧加热腔体内的自然对流。探讨了格拉晓夫数对流场、温度场以及热边界层厚度的影响，普朗特数对流速的影响。结果表明：压强梯度促使入侵流的分离。热边界层厚度在初始阶段只随时间变化，与格拉晓夫数无关，在对流稳定阶段，随格拉晓夫数增大而减小，随腔体高度线性增大。普朗特数为常数时，铅垂方向最大流速随格拉晓夫数增大而增大；普朗特数和格拉晓夫数都为常数时，铅垂方向最大流速随时间先增大后减小，最后达到稳定。

自然对流；流场；入侵流；热边界层厚度；铅垂流速

侧加热腔体内的自然对流是研究对流问题的经典流体力学模型之一，对这种对流现象的研究可以帮助人们理解工业内热交换器、太阳能热水器、核反应堆的原理以及自然界中存在的大洋热盐环流、地幔等由温差驱动的对流现象。

随着格拉晓夫数(Gr)增加，Yahata[1]给出侧加热腔体内运动表现出的不同行为：稳定→周期→有两个基本频率的准周期→混沌，混沌的过渡是由于相位锁定中断引起的。入侵流的分离是侧加热腔体内另一个重要物理过程，而分离是其最明显的初期瞬态特征[2]。Ivey[3]认为入侵流的分离是由腔体内部水跃导致的，Ravi[4]认为入侵流的分离是由热效应导致的，Xu[5]又认为边界层的卷入是水平入侵流分离的动力学机制。对此目前还没有一个明确的定论。徐丰利用实验和数值计算方法，研究了不同瑞利数下耦合热边界层向非定常周期性流动的演化[6]；描述了腔内非定常自然对流的突然侧加热的热边界层前缘效应 (LEE)以及水平入侵流的尾迹波[7]。薛宇轩和徐丰[8]利用二维数值模拟的方法研究了带中间隔壁的侧加热腔内自然对流与传热过程，结果发现瑞利数(Ra)和普朗特数(Pr)以及隔壁厚度是流动和传热的重要控制参数。

以上研究都是以小高宽比腔体为基础，本文以大高宽比(A=10)腔体为基础，对流场、温度场以及热边界层厚度δT进行了数值模拟研究，并探讨了不同工况下的对流情况：①Pr=6.949时，计算了13种不同Gr数下的对流情况。②计算了3种不同Pr工况下的对流情况。

1　数值模拟

1.1流体力学方程组

在Boussinesq假定下,描述这一问题的流体力学方程组可以表述为[9-14]：

质量密度的状态方程：

(1)

连续性方程：

(2)

动量方程：

(3)

热输运方程：

(4)

1.2边界条件

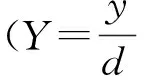
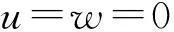
(5)

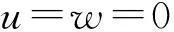
(6)

式中，Γ为计算区域高度；d为计算区域宽度，d=2 cm；A为腔体高宽比，A=10。

温度在上下壁面处热通量为0，在x=0,d处是等温的，所以，当Y=0,A时，有：

(7)

当X=0时，有：

(8)

当X=1时，有：

(9)

式中，ΔT为水平方向温度差。流速初始条件为u=w=0，初始温度取参考值293.15 K。

本文利用SIMPLE算法求解流体方程组，采用二阶迎风格式离散对流项和扩散项，而时间项采用一阶隐格式，时间步长为0.01 s。计算区域使用均匀交错网格系统，根据文献[11]研究结果，网格密度采用20×200。

2　数值模拟结果与分析

计算中，我们通过监测热侧壁面努塞尔数(Nu)随时间的变化来判定对流是否稳定。图1为热侧壁面Nu随时间的变化。从图中可以看出，t≤10 s时，Nu随时间急剧增大，10s≤t≤600 s时，Nu随时间减小，在t≥600 s后，Nu不再随时间变化，这说明对流已经稳定。这时的对流斑图可以作为给定Gr数情况下的稳定对流斑图。

图1　Gr=1.2×106时热侧壁面Nu随时间的变化Fig.1　Variation of Nu along the hot wall with time at Gr=1.2×106

2.1入侵流的演化过程

最初时段，由于热量通过导热传递给相邻流体时会造成侧壁面附近流体温度不均匀,进而引起密度不均匀,从而产生浮力。热侧壁面附近，浮升力大于流体自身重力和摩擦力，使流体沿右壁面向上运动；冷侧壁面附近，流体自身重力大于摩擦力，使流体沿左壁面向下运动，使得腔体角部区“空虚”(右下角和左上角)。沿侧壁爬行的流体抵达上下水平壁面时，受上下壁面阻碍，使铅垂方向流速迅速减小到0，这会引起腔体角部区压强显著增加。该压强梯度会驱动流体在水平方向上流动。图2为侧加热腔体内入侵流的发展过程。

图2　Gr=8.5×104时入侵流的演化过程Fig.2　Evolution process of intrusion flow at Gr=8.5×104

由图2可看出，t=1.5 s时，入侵流逐渐分离，热入侵流分离出现在腔体右上角(热边界层上角)，冷入侵流分离出现在腔体左下角(冷边界层下角)，入侵流沿水平方向流动。t=4.0 s时，热入侵流锋面抵达冷侧壁面，冷入侵流锋面抵达热侧壁面。此后，在侧壁面阻挡和侧壁面流动的吸卷作用下，冷侧壁面附近流体将热入侵流冷却并卷入带向腔体底部，热侧壁面附近流体将冷入侵流加热并卷入带向腔体顶部，如图2(d)所示。由于侧壁面附近流体不能将所有的入侵流卷入带走，一部分热流体会堆积在左上角，一部分冷流体会堆积在右下角，在左上角和右下角附近形成了一个“角形”密度场，如图2(e)所示。通过对入侵流演化过程与动力学机制分析，发现压强梯度促使入侵流的分离。

2.2Gr对流场和温度场的影响

对流稳定以后，图3给出了流函数ψ随Gr的变化，显示随着Gr增加，流函数由“椭圆形”分层逐渐变成“近似四边形”分层。图4给出了温度T随Gr的变化，显示随着Gr增加，温度场由线形分层逐渐变成“工”字形分层。图5给出了涡度ω随Gr的变化，显示随着Gr增加，涡度场腔体中线部逐渐出现一片“白化区”，并且随着Gr增加“白化区”宽度增大。

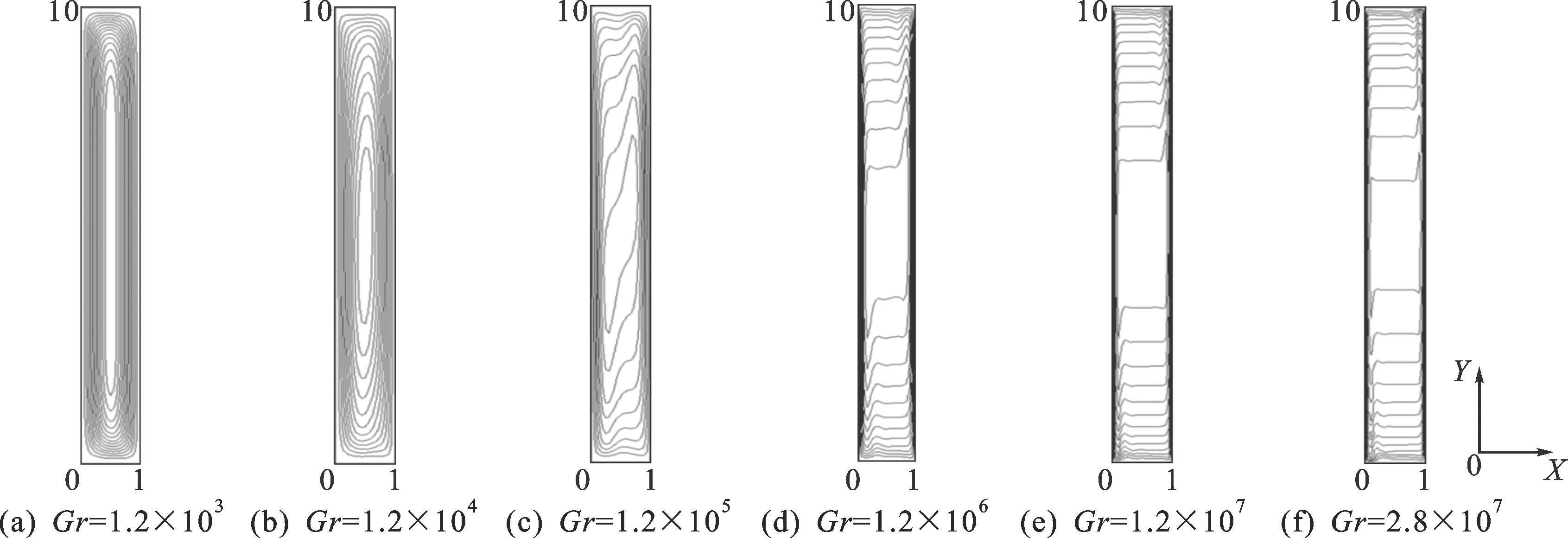
图3　ψ随Gr的变化Fig.3　Variation of ψ with Gr

图4　T随Gr的变化Fig.4　Variation of T with Gr

图5　ω随Gr的变化Fig.5　Variation of ω with Gr

为了确定温度在水平和铅垂方向上的分布情况，分别计算了Gr=1.2×104、Gr=1.2×105、Gr=1.2×106情况下，温度T在Y取1.6、3.2、4.8、6.4、8.0截面的水平方向分布(见图6)以及温度T在X取0.16、0.32、0.48、0.64、0.8截面的铅垂方向分布(见图7)。

图6　水平方向T的分布Fig.6　Distribution of T in horizontal direction

图7　竖直方向T的分布Fig.7　Distribution of T in vertical direction

由图6可看出，在Y=1.6水平截面上，温度先缓慢增加→相对稳定→迅速增加；在Y=8.0水平截面上，温度先迅速增加→相对稳定→缓慢增加。温度呈中心对称分布。另外，随着Gr增大，相对稳定区域的宽度逐渐增大，边界层厚度逐渐减小。Gr=1.2×104时，Y=4.8腔体高度处δT/d=0.332；Gr=1.2×105时，Y=4.8腔体高度处δT/d=0.235；Gr=1.2×106时，Y=4.8腔体高度处δT/d=0.146。所以，Gr越大，热边界层厚度越小。由图7可以看出，Gr越大，竖直截面之间的温度差越小，温度也是呈中心对称分布。

2.3Gr对热边界层的影响

对于突然加热的侧壁面，初始阶段，由于液体的黏性，侧壁面附近的热量主要是沿侧壁面法向方向传导[1,15-16]，因此在侧壁面附近会迅速形成热边界层，所谓热边界层就是侧壁面附近形成的温差相对较大的温度薄层。为了刻画热边界层厚度δT的影响因子，Patterson[16]通过量纲分析的方法将方程(4)中的时间项和热扩散项平衡，获得了δT量纲关系式，即δT～(κt)1/2。本文对δT进行无因次化处理，即δT/d。刻画了初始阶段δT/d随时间t的关系曲线，如图8所示。初始阶段，δT/d随时间迅速增加，0.15 s以后缓慢增加。当Gr=8.5×104时，发现初始阶段δT/d～t关系曲线与Gr=1.7×104和Gr=1.7×105时几乎一样，这说明Gr对初始阶段δT/d～t的关系曲线影响不大。

图8　初始阶段1/2腔体高度处δT/d随时间的变化Fig.8　Variation of δT/dwith time at the midheight in the initial stage

对流稳定以后，δT/d随腔体高度线性变化，如图9所示，发现δT/d随着腔体高度线性增加。拟合曲线关系式分别为:Gr=1.2×104时，δT/d=0.021 05Y+0.220 97,拟合度R2因子达0.978 46；Gr=1.2×105时，δT/d=0.013Y+0.171 39,拟合度R2因子达0.996 42；Gr=1.2×106时,δT/d=0.006 62Y+0.110 91,拟合度R2因子达0.961 4。

图9　δT/d随腔体高度的变化Fig.9　Variation of δT/d at the cavity height

2.4Pr对流场特性的影响

图10为Gr=1.7×105时流速场矢量分布图，可以清楚观察到流场的运动情况。

图10　流速场矢量图Fig.10　Vector diagram of velocity field

图11给出了不同腔体高度处铅垂方向流速w随X的变化。可以看出，w绝对值在冷边界层内先迅速增大，达到最大值后又迅速减小到0，在腔体中心区域流速在0附近波动。在热边界层内，w绝对值先迅速增大，达到最大值后又迅速减小到0，呈中心对称分布。

从图11明显可以看出，w绝对值的最大值发生在1/2腔体高度处边界层内。Gr=1.7×105时wmax=0.011 96 m/s。

图11　Gr=1.7×105时不同腔体高度处w随X的变化Fig.11　Variation of w with X at different heights when Gr=1.7×105

图12给出了铅垂方向最大流速wmax随Gr的变化。从图12(a)可以看出，随着Gr增大，wmax值先迅速增加，后缓慢增加。然后，又分别刻画了Pr=0.703 0和Pr=6.949 0情况下，Gr与wmax的关系曲线图。结果说明，wmax随Gr增大而增大。

图12　wmax随Gr的变化Fig.12　Variation of wmaxwith Gr

图13为初始阶段腔体内wmax随时间的变化。wmax随时间先增大后减小。时间t=14 s流速达到稳定，稳定流速为wmax=0.008 01 m/s。

图13　Gr=8.5×104时wmax随时间的变化Fig.13　Relation curve of wmaxwith time at Gr=8.5×104

3　结　论

本文通过二维流体力学方程数值模拟方法，研究了侧加热腔体内的自然对流。研究表明：压强梯度促使入侵流的分离；热边界层厚度增长是侧加热腔体内自然对流的重要物理过程之一，在初始阶段，热边界层厚度随时间变化，与Gr大小无关；对流稳定以后，热边界层厚度随Gr增大而减小,随腔体高度线性增大，Gr越大，线性斜率越小；Pr为常数时，Gr越大，热边界层厚度越小。

通过对流速场研究发现：腔体内铅垂方向流速绝对值的最大值发生在1/2腔体处的边界层内；Pr为常数时，铅垂方向的最大流速随Gr增大而增大；Pr和Gr都为常数时，腔体内铅垂方向的最大流速随时间先增大后减小，最后达到稳定。

[1]YAHATA H.Stability analysis of natural convection in vertical cavities with lateral heating[J].Journal of the Physical Society of Japan,1999,68(2):446-460.

[2]马丽娟，徐丰，胡非，等.侧加热腔体内重力波演化过程的数值模拟[J].力学与实践,2006,28(5):19-23.

MA Lijuan,XU Feng,HU Fei,et al.Numerical simulation of the formation and development of internal gravity wave in a differentially heated cavity[J].Mechanics and Engineering,2006,28(5):19-23.

[3]IVEY G N.Experiments on transient natural convection in a cavity[J]．Journal of Fluid Mechanics,1984,144:389-401.

[4]RAVI M R R,HENKES R A W M,HOOGENDOOM C J.On the high-Rayleigh-number structure of steady laminar natural-convection flow in a square enclosure[J].Journal of Fluid Mechanics,1994,262:325-351.

[5]XU F,PATTERSON J C,LEI C.Shadowgraph observations of the transition of the thermal boundary layer in a side-heated cavity[J].Experiments in Fluids,2005,38(6):770-779.

[6]徐丰.耦合热边界层的实验和数值研究[C]//中国空气动力学会.第九届全国实验流体力学学术会议论文：2013年卷.杭州:实验流体力学出版,2013:221-226.

XU Feng.Numerical and experimental studies of coupled thermal boundary layers[C]//China Aeromechanics Society.The Ninth China National Conference on Experimental Fluid Mechanics:2013 volume.Hangzhou:Journal of Experiments in Fluid Mechanics,2013:221-226.

[7]XU F,PATTERSON J C,LEI C.On the double-layer structure of the thermal boundary layer in a differentially heated cavity[J].International Journal of Heat and Mass Transfer,2008,51:3803-3815.

[8]薛宇轩,徐丰,杨庆山.侧加热分隔腔内的流动与传热[C]//北京力学会.北京力学会第20届学术年会论文集：2014年卷.北京:北京力学会出版,2014:113-114.

XUE Yuxuan,XU Feng,YANG Qingshan.The flow and heat transfer in a differentially heated cavity with bulkhead[C]//Beijing Society of Theoretical and Applied Mechanics.Twentieth Annual Conference of Beijing Mechanics Association:2014 volume.Beijing:Beijing Society of Theoretical and Applied Mechanics,2014:113-114.

[9]宁利中,周洋,王思怡,等.Poiseuille-Rayleigh-Benard流动中的局部行波对流[J].水动力学研究与进展，2010,25(3):299-306.

NING Lizhong,ZHOU Yang,WANG Siyi,et al.Localized traveling wave convection in Poiseuille-Rayleigh-Benard flows[J].Chinese Journal of Hydrodynamics,2010,25(3):299-306.

[10]宁利中,王娜,袁喆,等.分离比对混合流体Rayleigh-Benard对流解的影响[J].物理学报,2014,63(10):273-279.

NING Lizhong,WANG Na,YUAN Zhe,et al.Influence of separation ratio on Rayleigh-Benard convection solutions in a binary fluid mixture[J].Acta Physica Sinics,2014,63(10):273-279.

[11]宁利中,余荔,袁喆,等.沿混合流体对流分叉曲线上部分支行波斑图的演化[J].中国科学G辑，2009，39(5):746-751.

NING Lizhong,YU Li,YUAN Zhe,et al.The evolution of traveling wave pattern along the upper branch of convective bifurcation curves in a binary fluid mixture[J].Science in China G,2009,39(5):746-751.

[12]宁利中,齐昕,周洋,等.混合流体行波对流中的缺陷结构[J].物理学报,2009，58(4):2528-2534.

NING Lizhong,QI Xin,ZHOU Yang,et al.Defect structures of Rayleigh-Benard travelling wave convection in binary fluid mixtures[J].Acta Physica Sinics,2009,58(4):2528-2534.

[13]齐昕,宁利中，刘嘉夫，等.极小长高比腔体内混合流体Undulation行波对流[J].力学季刊,2014,35(2):253-261.

QI Xin,NING Lizhong,LIU Jiafu,et al.Undulation traveling wave convection in binary fluid mixtures in a small-aspect-ratio cell[J].Chinese Quarterly of Mechanics,2013,34(4):253-261.

[14]王卓运,宁利中，王娜，等.基于振幅方程组的行波对流的数值模拟[J].西安理工大学学报,2014,30(2):163-169.

WANG Zhuoyun,NING Lizhong,WANG Na,et al.Numerical simulation of traveling wave convection based on amplitude equations[J].Journal of Xi’an University of Technology,2014,30(2):163-169.

[15]徐丰,崔会敏.侧加热腔内的自然对流[J].力学进展,2014,44(3):1-40.

XU Feng,CUI Huimin.Natural convection in a differentially heated cavity[J].Advances in Mechanics,2014,44(3):1-40.

[16]PATTERSON J C.On the existence of an oscillatory approach to steady natural convection in cavities[J].International Communications in Heat and Mass Transfer,1984,106:104-108.

(责任编辑周蓓)

Study of the convection in a differentially heated cavity

LI Kaiji1，NING Lizhong1，NING Bibo2，TIAN Weili3

(1.State Key Laboratory Base of Eco-hydraulic Engineering in Arid Area，Xi’an University of Technology,Xi’an 710048,China；2.College of Civil Engineering and Architecture,Jiaxing University,Jiaxing 314001,China;3.College of Fine Arts,Shanghai University,Shanghai 200444,China)

Natural convection of heating from side wall is investigated by means of numerical simulation of 2-D equations of hydrodynamics.The paper studies the influence of Grashof number on flow field,temperature field and the thickness of thermal boundary layer and the influence of Prandtl number on velocity.Results show that the pressure gradient causes the separated intrusion flow.The thickness of thermal boundary layer changing only with time has nothing to do with Grashof number in the initial phase,but in the stable phase,the thickness of thermal boundary layer decreases obviously with increasing Grashof number,and it increases obviously with cavity height.The vertical-velocity increases with Grashof number when Prandtl number is constant.The vertical-velocity firstly increases and then decreases with time,and finally reaches its stability when Grashof number and Prandtl number are constant.

natural convection; flow field; intrusion flow；thermal boundary layer thickness; vertical velocity

10.19322/j.cnki.issn.1006-4710.2016.01.010

2015-09-01

国家自然科学基金资助项目(10872164)；陕西省重点学科建设专项资金资助项目(00X901)

李开继，男，硕士生，研究方向为水力学和对流动力学。E-mail:348285456@qq.com

宁利中，男，教授，博士。研究方向为对流动力学和高速水力学。E-mail:ninglz@xaut.edu.cn

O357

A

1006-4710(2016)01-0052-06