基于变换光学的光学重叠效应

臧小飞,计学斌,朱亦鸣（上海理工大学上海市现代光学系统重点实验室,上海 200093）

基于变换光学的光学重叠效应

臧小飞,计学斌,朱亦鸣
（上海理工大学上海市现代光学系统重点实验室,上海 200093）

基于变换光学理论,提出了一种新型的各向异性均匀的压缩变换介质。通过坐标变换,该压缩变换介质将一片选定的均匀各向同性的自由物理空间“压缩”至一个小的变换区域,并通过补偿介质（ε=μ=—1）来补偿除了压缩区域之外的那片自由空间,以保持空间场分布的连续性。当两个分离的点光源分别处于该压缩变换介质之中的时候,它们能够形成完美的光学重叠效应,即形成完美的光学相干效应。利用有效介质理论,可以进一步简化变换介质参数,获得各向同性均匀的压缩变换介质实现光学重叠效应。该研究在高能相干激光中具有潜在的应用。

变换光学；光学重叠；有效介质理论

引 言

近十几年来,超颖材料技术的发展,使得人们可以任意操控电磁波的振幅、偏振、相位以及传播路径等。该技术为人们探索新的物理机制,设计新的物理器件提供了一条崭新的途径。2006年Pendry等［1］和Leonhart［2］分别提出了一套精确调控电磁波的理论—变换光学理论。目前,变换光学为设计基于超颖材料的电磁波调控新器件提供了理论依据。利用变换光学方法并假设在虚拟弯曲空间中传播的电磁波是沿着弯曲路线传输,那么我们就可以构建实际物理空间和虚拟弯曲空间的一一对应关系。根据麦克斯韦方程的变换不变性,在实际物理空间中获得电磁波沿着弯曲路线传输所需要的变换介质,通过设置相应的变换介质实现电磁波的精确调控［3］。其中,隐身大衣作为变换光学的一个典型应用,在变换光学理论提出之初即引起了广泛的研究,包括圆形隐身大衣、方形隐身大衣、椭圆形隐身大衣和任意形状的隐身大衣［4-8］。此外,根据变换光学理论,人们还研究了波集中器、波旋转器、波连接器、波分束器以及人工电磁黑洞等［9-13］。

最近,赖耘等基于变换光学和负折射材料提出了空间折叠原理,并由此设计出基于补偿介质的外部隐身大衣［14］。与传统隐身大衣不同,该类型的隐身大衣可以实现被隐藏的物体看到外界的物体,而电磁波却探测不到被隐藏的物体。基于空间折叠原理,赖耘等又提出了幻觉变换介质,该介质可以实现将一个物体变换成另一个物体的光学幻觉效应（如将一个勺子变成一个杯子）［15］。同时,基于空间折叠原理,徐亚东等提出了基于补偿介质理论的光学重叠效应（即反镜像效应）,形成两个形状不同的物体的相互重叠幻觉效应［16］。此外,我们已在此基础上实现了两个形状相同的物体的相互重叠幻觉效应,并实验验证光学完美相干效应［17-18］。到目前为止,以上报道的所有光学重叠效应均基于各向异性均匀或者非均匀介质实现,导致材料参数和实验制备相当复杂。能否利用各向同性且均匀的变换介质获得光学重叠效应是目前的一大挑战。基于此,本文提出了另一类新型压缩变换介质并结合有效介质理论,实现了层状化的各向同性且均匀的变换介质并诱导产生光学重叠效应。

1　理论模型

图1（a）为实现光学重叠效应所需的变换介质的结构示意图及其仿真区域。区域Ⅰ-Ⅵ为压缩介质区,区域Ⅶ为补偿介质区:（1）区域AEEDC1B1被压缩至区域ABCDC1B1,其中区域AEBB1被压缩至区域Ⅱ中,区域EECC1B1B被压缩至区域Ⅰ中,区域EDC1C被压缩至区域Ⅵ中；（2）区域ABCDE1E1被压缩至区域AEEDE1E1,其中区域ABEE1被压缩至区域Ⅲ中,区域BCEE1E1E被压缩至区域Ⅳ中,区域CDE1E被压缩至区域V中；（3）由于区域ABCDEE被两次压缩进区域ABCDC1B1和区域AEEDE1E1中,所以区域Ⅶ必须设置补偿介质来抵消其中两次压缩产生的空间重复。在直角坐标系下各点坐标为: A（—a—d,0）,B（—a,d）,C（a,d）,D（a+d,0）,E（a,—d）,E（—a,—d）,B1（—a,2d）,C1（a,2d）, E1（a,—2d）,E1（—a,—2d）,其中a=0.3 mm,d=0.3 mm。根据以上对压缩区和补偿介质区的描述,相应的变换方程满足:

区域Ⅰ和Ⅳ:

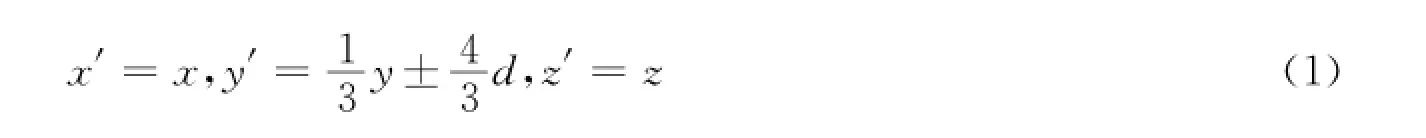
区域Ⅱ和Ⅴ:

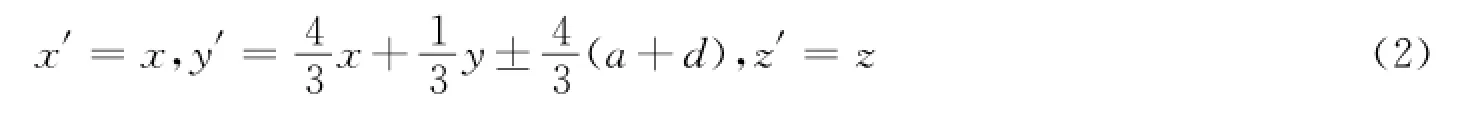
区域Ⅲ和Ⅵ:

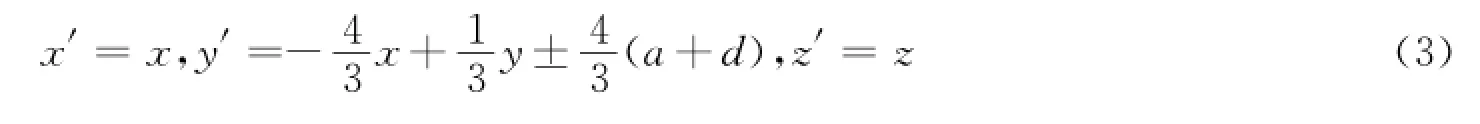
区域Ⅶ:

其中“+”对应区域Ⅰ,Ⅱ或Ⅵ；“—”对应区域Ⅲ,Ⅳ或V。（x,y,z）为物理空间坐标,而（x′,y′,z′）为虚拟（被压缩）空间坐标。根据变换光学原理,区域Ⅰ-Ⅶ对应的变换介质的电磁参数为:

区域Ⅰ和Ⅳ:

区域Ⅱ和Ⅴ:

区域Ⅲ和Ⅵ:

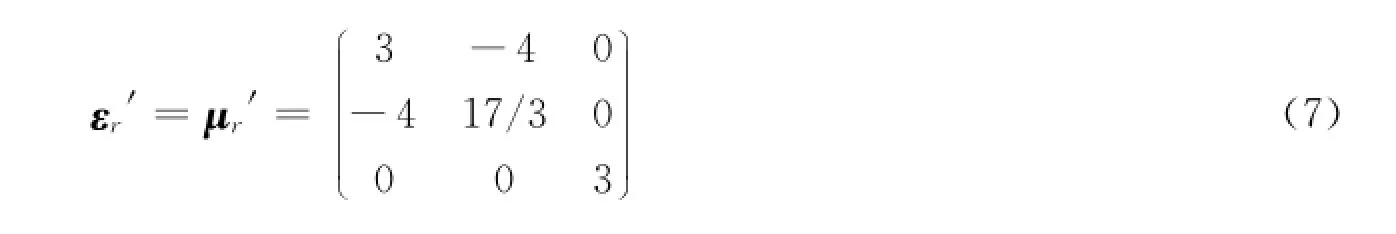
区域Ⅶ:

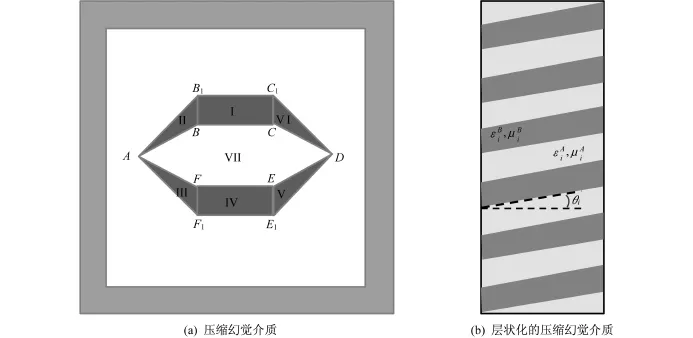
图1　各向同性非均匀和各向同性均匀的层状幻觉介质结构示意图Fig.1　Schematic of the isotropic，inhomogenous and homogenous illusion media structure

在本文的讨论中我们只考虑TM（横磁）波和二维结构,由此各区域的电磁参数可以简化为:区域Ⅰ和Ⅳ:

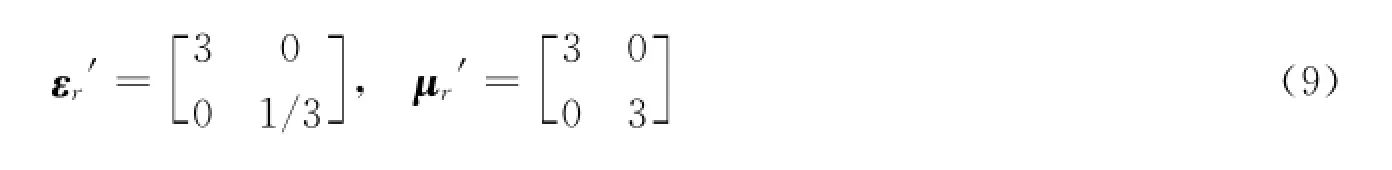
区域Ⅱ和Ⅴ:

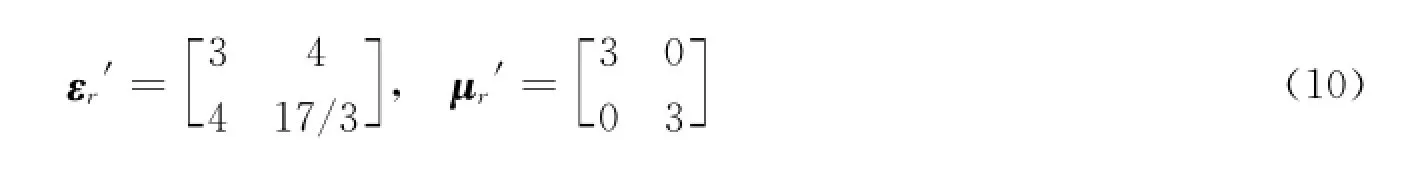
区域Ⅲ和Ⅵ:

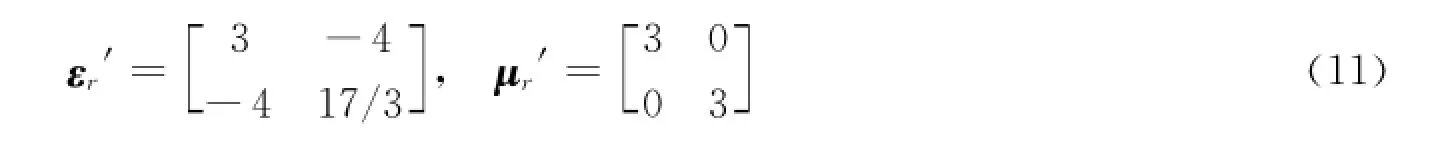
区域Ⅶ:

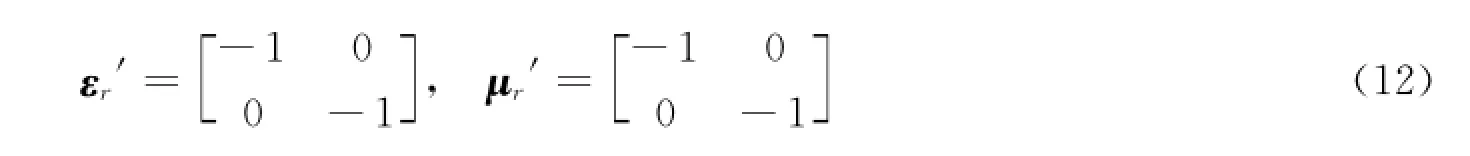
区域Ⅰ～Ⅵ中的电磁材料参数是针对均匀的各向异性材料,根据有效介质理论,各向异性均匀材料可以用对应的两种交替排列的各向同性材料来替代（如图1（b）所示）,若假设两种各向同性材料的厚度相等,则有相应的介质参数:

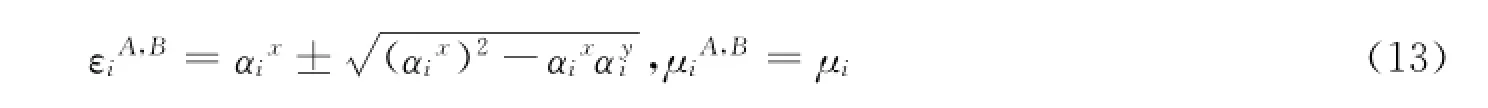
2　结果及分析

通过COMSOL软件计算,可以得到自由空间和存在压缩幻觉介质时的磁场分布。图2（a）给出了频率为1 THz的TM波在45°斜入射情况下,自由空间和各向异性均匀幻觉介质（介质参数满足式（9）～（12））中的磁场分布。图2（b）给出相同频率的TM波在45°斜入射情况下,在自由空间中传播的磁场分布。由变换式（1）～（4）可知,自由空间Ⅰ、Ⅱ、Ⅵ和Ⅶ被压缩进变换区域Ⅰ、Ⅱ、Ⅵ,所以变换区域Ⅰ、Ⅱ、Ⅵ包含了自由空间Ⅰ、Ⅱ、Ⅵ和Ⅶ中的场分布（即图2（a）中区域Ⅰ、Ⅱ、Ⅵ中的场等效于图2（b）中黑色实线区域中的场）。同样,变换区域Ⅲ、Ⅳ、V也包含了自由空间Ⅲ、Ⅳ、V和Ⅶ中的场分布（即图2（a）中区域Ⅲ、V、Ⅵ中的场等效于图2（b）中黑色虚线区域中的场）。由此可知,自由空间Ⅶ被同时压缩进上下两个变换介质区。为了保证空间的连续性,必须在区域Ⅶ中设置相应的补偿介质（介质参数如式（8））,这样,就能保证补偿介质区域Ⅶ中的磁场分布传播方向与外部自由空间上的磁场传播方向正交。

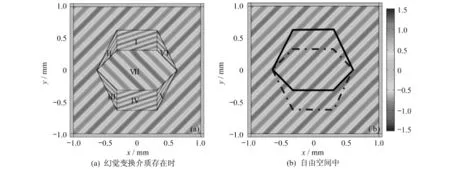
图2　有/无幻觉介质情况下的磁场分布Fig.2　Magnetic field distributions with/without the illusion media

比较图2（a）和（b）,可以发现电磁波在透过变换幻觉介质后,其场分布和自由空间上传播的电磁波完全一样。此外,由于自由空间Ⅶ被同时压缩进上下两个变换介质区,所以压缩区域Ⅰ、Ⅱ、Ⅵ和压缩区域Ⅲ、V、Ⅵ必将有部分区域是相互重叠的,其重叠部分表现在自由空间如图2（b）中实线黑色区域和虚线黑色区域的交叠部分。根据这一特性,我们设计的幻觉变换介质可以实现光学重叠效应。

图3（a）为自由空间中分别处于（0,0.5 mm）和（0,—0.5 mm）的两个完全相同的点源的磁场分布（相应的振幅均为1 V,波长为0.33 mm）。从图3（a）的磁场分布可以看出,分离的两个完全相同的点源在自由空间上产生了相干效应（包括相长干涉和相消干涉）。图3（b）为嵌入在移动介质Ⅰ区域（0,0.5 mm）处和Ⅳ区域（0,—0.5 mm）处的两个完全相同的点源的磁场分布（相应的振幅均为1 V,波长为0.33 mm）。而图3（c）为自由空间中处于（0,0）处振幅为2 V,波长为0.33 mm的单个点源的磁场分布。比较图3（b）和图3（c）可以发现,两者在变换区域外的场分布完全一致。这表明图3（b）两个振幅均为1 V,波长为0.33 mm的分离的点源,在移动介质的作用下,全部移动至（0,0）处,并完全重叠在一起,等效于一个振幅为2 V,波长为0.33 mm的点源,实现了压缩变换介质的完美光学重叠效应。

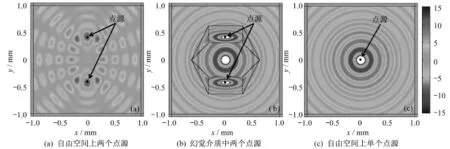
图3　不同介质中的点源磁场分布Fig.3　Magnetic field distributions with different conditions

由于很难找到各向异性均匀的介质实现以上所述的完美光学重叠效应,为此从实际应用角度出发进一步简化介质参数。根据第一部分的讨论,结合坐标变换和有效介质理论,将原先的各向异性均匀的介质变换成各向同性均匀的层状介质,以符合实际应用。图4（a）为各向同性均匀的层状变换压缩介质产生的光学重叠效应,嵌入在层状移动介质I区域（0,0.5 mm）处和Ⅳ区域（0,—0.5 mm）处的两个完全相同的点源（振幅为1 V,波长为0.33 mm）的磁场分布等效于图4（b）中自由空间中处于（0,0）处振幅为2 V,波长为0.33 mm的单个点源的磁场分布。这表明,我们所设计的层状各向同性均匀的变换压缩介质同样可以实现完美光学重叠效应。

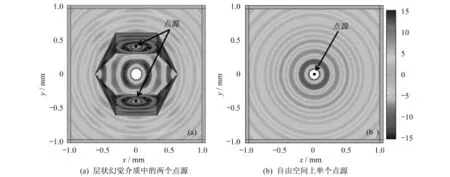
图4　层状幻觉介质和自由空间上的点源磁场分布Fig.4　Magnetic field distributions in the layered illusion media and the free space

3　结 论

通过变换光学理论及基于坐标变换,我们设计了一类压缩变换介质。利用该压缩变换介质,我们实现了两个点光源的空间完美相干效应（相长相干）。通过将坐标变换和有效介质结合,实现了各向同性均匀的层状压缩变换介质。经COMSOL数值仿真,对压缩变换介质形成的光学完美相干效应/光学重叠效应进行了验证。

［1］ PENDRY J B,SCHURIG D,SMITH D R.Controlling electromagnetic fields［J］.Science,2006,312（5781）:1780-1782.

［2］ LEONHART U.Optical conformal mapping［J］.Science,2006,312（5781）:1777-1780.

［3］ SCHURIG D,PENDRY J B,SMITH D R.Calculation of material properties and ray tracing in transformation media［J］.Optics Express,2006,14（8）:9794-9804.

［4］ IYSIC B,SIPUS Z,HRABAR S.Analysis of uniaxial multilayer cylinders used for invisible cloak realization［J］.IEEE Transactions on Antennas and Propagation,2009,57（5）:1521-1527.

［5］ JIANG W X,CUI T J,YU G X,et al.Arbitrarily elliptical-cylindrical invisible cloaking［J］.Journal of Physics D:Applied Physics, 2008,41（8）:085504.

［6］ LI C,YAO K,LI F.Two-dimensional electromagnetic cloaks with non-conformal inner and outer boundaries［J］.Optics Express, 2008,16（23）:19366-19374.

［7］ LI W,GUAN JG,SUN Z G,et al.A near perfect invisibility cloak constructed with homogeneous materials［J］.Optics Express,2009, 17（26）:23410-23416.

［8］ HAN T C,QIU C W,TANG X H.The general two-dimensional open-closed cloak with tunable inherent discontinuity and directional communication［J］.Applied Physics Letters,2010,97（12）:124104.

［9］ CHEN H Y,CHAN C T.Transformation media that rotate electromagnetic fields［J］.Applied Physics Letters,2007,90（24）:241105.

［10］ RAHM M,SCHURIG D,ROBERTSD A,et al.Design of electromagnetic cloaks and concentrators using form-invariant coordinate transformations of Maxwell's equations［J］.Photonics and Nanostructures-Fundamentals and Applications,2008,6（1）:87-95.

［11］ RAHM M,CUMMER S A,SCHURIG D,et al.Optical design of reflectionless complex media by finite embedded coordinate transformations［J］.Physical Review Letters,2008,100（6）:063903.

［12］ ZHANG K,WU Q,MENG F Y,et al.Arbitrary waveguide connector based on embedded optical transformation［J］.Optics Express, 2010,18（16）:17273-17279.

［13］ CHEN H Y,MIAO R X,LI M.Transformation optics that mimics thesystem outside a Schwarzschild black hole［J］.Optics Express, 2010,18（14）:15183-15188.

［14］ LAI Y,CHEN H Y,ZHANG Z Q,et al.Complementary media invisibility cloak that cloaks objects at a distance outside the cloaking shell［J］.Physical Review Letters,2009,102（9）:093901.

［15］ LAI Y,NG J,CHEN H Y,et al.Illusion optics:the optical transformation of an object into another object［J］.Physical Review Letters,2009,102（25）:253902.

［16］ XU Y D,DU S W,GAO L,et al.Overlapped illusion optics:a perfect lens brings a brighter feature［J］.New Journal Physics,2011,13（2）:023010.

［17］ ZANG X F,JIANG C.Overlapped optics,illusion optics,and an external cloak based on shifting media［J］.Journal of the Optical Society of America B,2011,28（8）:1994-2000.

［18］ LI JJ,ZANG X F,MAO J F,et al.Overlapped optics induced perfect coherent effects［J］.Scientific Reports,2013,3:3569.

（编辑:刘铁英）

Overlapped optics based on transformation optics

ZANG Xiaofei,JI Xuebin,ZHU Yiming
（Shanghai Key Laboratory of Modern Optical System,University of Shanghai for Science and Technology,Shanghai 200093,China）

In this paper,based on transformation optics,a new anisotropic and homogenous compressible transformation media is proposed.By using the coordinate transformation,such compressible transformation media can be able to compress the selected isotropic and homogenous free space into a small transformation regime.Meanwhile,the corresponding compensating medium（ε=μ=—1）is introduced into the selected free space（except for the transformation regime）in order to keep the continuity of the field distribution.When two separated point sources embedded in such a transformational media,all of them can overlap with each other,leading to the perfect optical interference effect.By using the effective medium theory,such transformational media can be further simplified,and an isotropic and homogenous compressible transformation media is obtained to realize the overlapped optics. Our investigation may have potential application in high power coherent laser beams.

transformation optics；overlapped optics；effective medium theory

TN 2

A

10.3969/j.issn.1005-5630.2016.02.007

1005-5630（2016）02-0128-06

2015-10-08

国家重大基础研究项目973计划（2014CB339806）；国家自然科学基金（61307126,61138001）；上海市教委科研创新项目（14YZ093）

臧小飞（1981—）,男,副教授,主要从事太赫兹器件方面的研究。E-mail:xfzang@usst.edu.cn

朱亦鸣（1979—）,男,教授,主要从事太赫兹技术方面的研究。E-mail:ymzhu@usst.edu.cn