基于动态散斑的颗粒流模式转变机理研究

马　生,杨　晖,李　然,盛旭波,郑　刚,王世豪,姚　鑫（.上海理工大学光电信息与计算机工程学院,上海 00093；.上海理工大学医疗器械与食品学院,上海 00093）

基于动态散斑的颗粒流模式转变机理研究

马生1,杨晖1,李然1,盛旭波1,郑刚2,王世豪1,姚鑫1
（1.上海理工大学光电信息与计算机工程学院,上海 200093；2.上海理工大学医疗器械与食品学院,上海 200093）

颗粒流模式转变的研究具有重要的理论和现实意义,以滚筒内的颗粒流作为研究对象,采用动态散斑测量法研究了颗粒流的间歇崩塌和连续流动2种模式之间的转变机理。目的是利用动态散斑方法对滚筒颗粒运动进行研究,并尝试从两种状态持续时间的概率分布上对其转变机理做出阐述。通过CCD相机得到散斑图像,对散斑图像做对比度分析得到滚筒内颗粒运动速度跟时间的图像,进而提取出崩塌时间、连续时间、崩塌持续时间、崩塌间隔时间,并对其进行分布统计、曲线拟合、结果显示,两种状态转变不是突变性,而是存在一个2种状态共存的过渡状态,并且是随着各自的存在概率变大或者变小而逐渐地稳定下来。

颗粒流；崩塌模式；连续流；过渡状态；动态散斑

引 言

颗粒态在自然界广泛存在,尺度在1～104μm范围的物质都可称为颗粒物质,砂砾、烟尘、泥土、粮食以及药品都是颗粒物质［1-2］。在外力和内部应力作用下,使得颗粒物质发生的类似流体的运动状态,我们称之为颗粒流动。在自然界中颗粒流动广泛存在,比如山体滑坡、河流运动、工业生产以及人的呼吸、血液流动等等［3］。2014年,李家春院士主编了《中国学科发展战略:流体动力学》,把“颗粒物质与颗粒流”确定为6个基础与前沿学科之一［4］。

在对颗粒态的研究过程中,对由一种流态进入另一种流态的过渡过程的研究是十分有意义的,自然界中滑坡、泥石流、雪崩的发生都包含这样的过渡过程,研究其过渡机理可以让我们提前预防、避免自然灾害的发生；其次,工农业生产中制药、陶瓷、水泥、冶金中了解其过渡过程,可以更好的指导我们工业生产。

在研究颗粒运动的几类实验装置中,滚筒结构简单,易于观察和控制（当几何结构确定,转速是控制流动的唯一参数）,并且在工业上应用相当广泛,因此,滚筒中颗粒物质的运动研究成为研究热点。当滚筒转速较低时,滚筒内颗粒运动呈现间歇的崩塌状态（DA）,当滚筒转速较大时,滚筒内颗粒运动呈现连续流动状态（CF）,在两个速度之间,随着滚筒转速的提高,颗粒运动状态也逐渐的发生改变。早先Rajchenbach［5］研究认为,滚筒颗粒在低速崩塌与高速连续变换过程是一种滞回状态,即随滚筒转速变化,筒内颗粒运动状态的变化是瞬间完成的,并且在滚筒转速由低到高变化和由高到低变化两种情况下,发生颗粒运动状态变化时的速度不同。而后面Fischer等［6］发现,滚筒内颗粒运动状态的过渡不是瞬间完成,而是存在一个滚筒速度范围,在这个范围内两种颗粒运动状态同时存在。

关于滚筒中颗粒运动状态发生改变的机理有不同的阐述。Rajchenbac认为崩塌状态和连续流状态中颗粒向下滚落过程持续时间的差异导致了颗粒运动状态的改变。Benza等［7］则认为在颗粒运动状态转变过程中起重要作用的是颗粒之间的摩擦力。而Fische等在最近的研究中得出,滚筒中颗粒在临界转速范围及一定观察时间内均可单独出现或两者共存,其中,崩塌过程中随滚筒转速提高,产生的随机干扰使体系在两种运动状态下相互转换。因此,对于滚筒中颗粒运动状态转变的机理引起了新一轮探讨。

动态散斑法（dynamic speckle,DS）是近年开发的一种研究软物质微观动力学过程的新方法［8］。DS技术的特点是时空分辨率高、穿透性好等,已被用于溶液中颗粒的扩散运动、沙堆的崩塌［9］、泡沫的粗化过程［10］等研究。

本论文选择直径为0.4～0.6 mm的玻璃珠,利用可调速滚筒装置,使用DS方法［11-12］,对这一现象进行研究并尝试从数学概率论角度对现象做出解释。

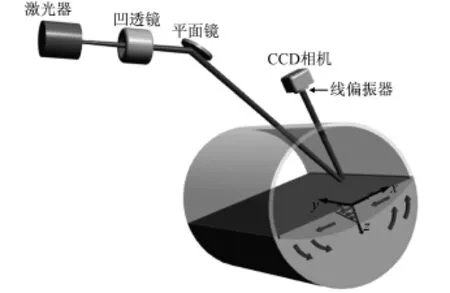
图1　滚筒装置示意图Fig.1　Schematic of the experimental setup

1　实 验

1.1实验装置

实验装置示意图如图1所示,滚筒内径为140 mm,前后端盖相距200 mm,滚筒为透明玻璃构成,滚筒平放在4个底座固定在滚轴的驱动轮上。滚筒由4个同步轮驱动,采用德国Dunker公司的直流电机和行星减速器,通过闭环控制使得滚筒转速Ω在0～25（°）/s范围内旋转。

实验选用RGB公司的NovaPro DPSS激光器（波长为532 nm,功率为300 mW）,入射激光通过凹透镜扩束,再由平面镜反射,入射到滚筒内颗粒物质表面。检测器选用DALSA公司的spyder系统线阵CCD相机（1024像素,每个像素尺寸为14μm,最大线速率68 k Hz）,并在相机表面固定中心波长532 nm的滤光片,滤除环境杂散光。

实验选用的颗粒为烘干过筛直径0.4～0.6 mm的球形玻璃珠。滚筒的颗粒填充率为30%。当颗粒类型、大小、干燥程度以及滚筒中颗粒填充程度确定以后,实验中的唯一控制变量变为滚筒转速Ω。

1.2DS方法原理

DS法的原理如图2（a）所示,激光经过凹透镜扩束后照射在颗粒物质表面,再经过颗粒间多次散射后在空间产生干涉,并形成如图2（b）所示的“散斑”。当被测颗粒物质运动时,散斑图像也会产生相应的波动,称为“动态散斑”（也称为“时变散斑”）。通过计算散斑图像的对比度就可以得到测量区内颗粒的位移变化,最后测得颗粒速度波动,即颗粒速度波动（δv）。对于作无序运动的颗粒,散斑的波动速率与颗粒的速度波动（δv）有关,因此通过计算线阵CCD相机表面的散斑图像波动（自相关函数）随时间变化,就可以计算出相应的颗粒速度波动随时间变化,如图2（c）所示。

图2　DS法测量系统及原理图Fig.2　DSmeasurement system

根据统计光学理论［13］,散斑的对比度V2（T）可以表示为散射光强I的“波动方差”与“均值平方”之比

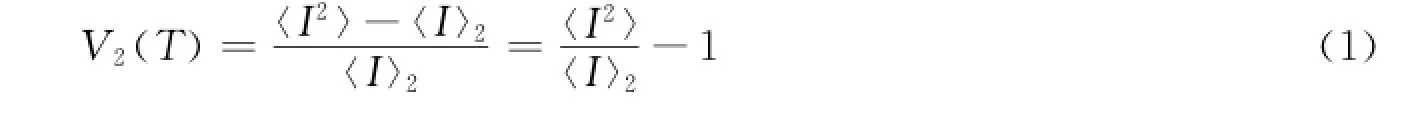
其中

式中:N为CCD相机的像素数；xi,T为CCD相机第i个像素在曝光时间T下输出的灰度值x。其中

根据Siegert公式

式中:β称为系统的相干因子；g1（t）为散射光场自相关函数。将式（4）代入式（2）得

再将式（5）代入式（1）得到散斑图像的对比度

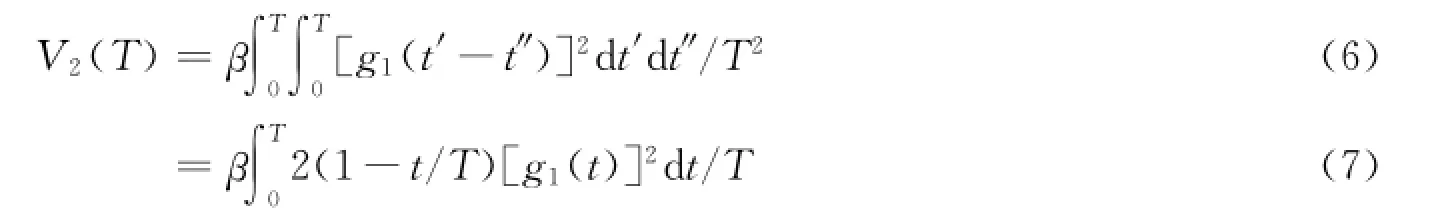
这样就建立了散斑图像对比度与散射光场自相关函数g1（t）的关系。

根据扩散波光谱理论,光子在颗粒间扩散传播,其散射场自相关函数为

式中:P（s）为光子传播路径s的概率分布；〈Δr2（t）〉为颗粒均方位移；〈Δr2（t）〉=〈δv·t〉2,δv为所求的颗粒运动速度波动；k0=2πn0/λ为散射波矢；n0为介质（空气）的折射率；λ为入射光波长；l*为光子传播的平均自由程。

对于颗粒样品厚度为L的后向散射结构,且样品厚度足够大（L≫l*）,根据文献［13］,公式可简化为

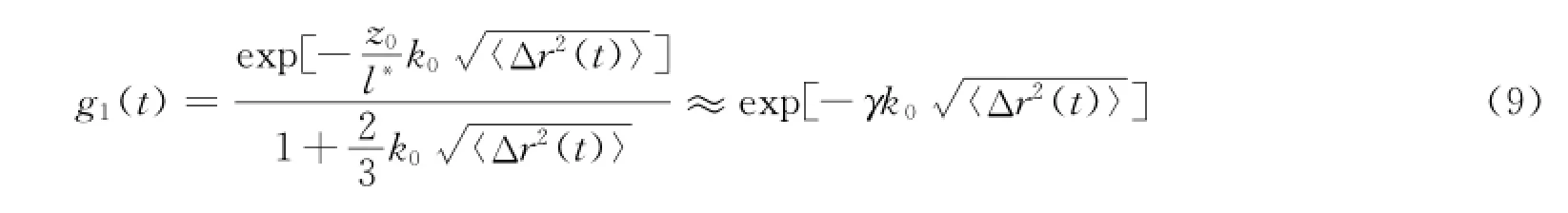
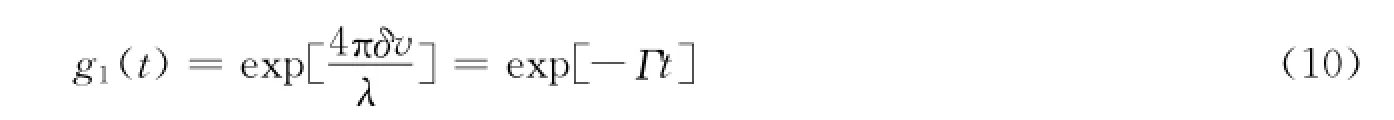
式中:Γ称为自相关函数g1（t）的衰减线宽。

将式（10）代入式（7）并积分,可以得到散斑对比度V2（T）与衰减线宽Γ的关系

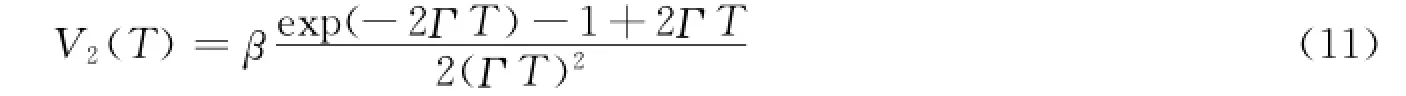
为了消除系统的相干因子β,可以将原数据中的每2组数据叠加,得到2倍曝光时间下散斑图像,再用相同的方法得到2倍曝光时间下的V2（2T）,最后将2组对比度相除就可以消去系统的相干因子β。

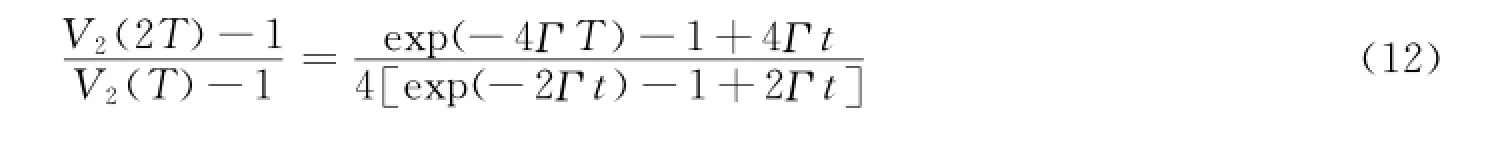
1.3实验方案

验证DS方法的可适用性。（1）滚筒转速由低到高逐渐变化,初始转速为1.067（°）/s,转速间隔0.213（°）/s,每个转速下,保持5 min的运行时间,保证滚筒在此转速运行平稳,结果稳定。观察并记录每个转速下,滚筒内颗粒运动状态,并找出出现过渡状态时的滚筒转动速度区间为1.067～2.453（°）/s。（2）分别取1.1～2.5（°）/s中间11个转速,利用DS方法测得动态散斑图像。（3）对得到的动态散斑图像用MATLAB进行处理,提取特征参数,并将分析结果跟已知的实验结果相比对,验证DS方法研究滚筒中颗粒运动的可适用性。

2　实验结果

实验中滚筒内颗粒在滚筒转速为1.493（°）/s时开始进入过渡状态,即滚筒颗粒运动开始出现连续流动状态（CF）；滚筒转速在1.920（°）/s时,颗粒间歇崩塌状态（DA）与连续流动状态（CF）各自持续时间近似相等,并且依次交替出现；滚筒转速在2.240（°）/s时,滚筒内颗粒运动状态全部为连续流动（CF）。

3　分析与讨论

3.1过渡过程DA与CF的共存

图3所示（a）是滚筒转速在1.920（°）/s下,测量时间600 s下滚筒内颗粒运动速度平方随时间的变化。图中为440～540 s时间内的颗粒速度平方随时间变化的曲线。并通过阈值法,区分出颗粒崩塌部分（实线）和连续部分（虚线）；（b）是（a）图中虚线部分放大图像。

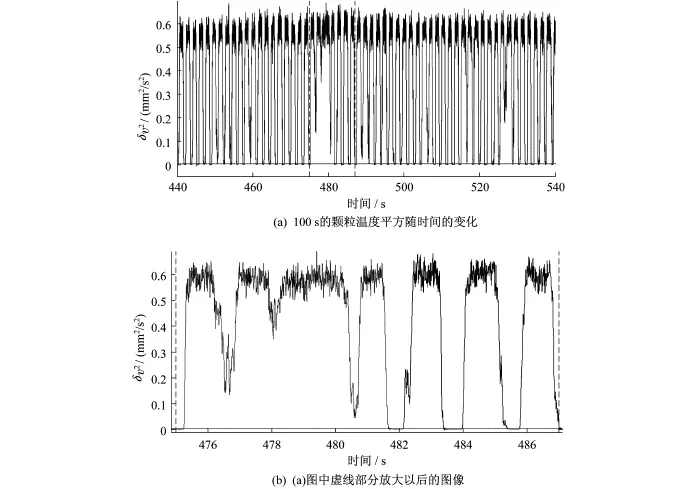
图3　过渡状态时滚筒颗粒速度平方随时间的变化Fig.3　Time evolution of square particle flection velocity

阈值法区分崩塌状态跟连续流状态:首先取一个阈值0.004画一条直线如图底部虚线所示,其中直线会跟原曲线有很多交点,当相邻交点距离大于一般崩塌持续时间1.5倍时（一般崩塌持续时间需根据实际曲线观察获得）,认为此时滚筒内颗粒运动进入连续流状态,并记录其开始与停止时间,其余部分则认为是崩塌状态。

图3显示了过渡状态中崩塌跟连续流相互交替出现的情况,符合实际观察到的颗粒运动状态。最底部虚线是阈值法区分崩塌跟连续流时所选的阈值,其中实线部分是颗粒运动处在崩塌状态,而虚线是表示颗粒运动处在连续流状态。情况与Fischer的论文结果是一致的。

3.2DA与CF各自出现时间的统计分布研究

图4（a）是滚筒转速在1.920（°）/s下,测量时间为3 500 s下滚筒内颗粒崩塌持续时间tda的统计直方图,图（b）是滚筒转速在1.920（°）/s下,测量时间为3 500 s下滚筒内颗粒连续流持续时间tcf的统计直方图。

从图中可以看出,无论崩塌还是连续流,出现次数最多的集中在左侧,即持续时间较短的多次出现,而持续时间较大的则很少出现。说明滚筒中颗粒运动处于过渡状态时,崩塌跟连续依次紧密重复出现。崩塌持续时间统计直方图左端有一个时间间隔是因为崩塌持续时间至少要等于一个崩塌周期,而前面间隔时间至少为一个崩塌周期时间；连续状态持续时间直方图左端有一个时间间隔是因为根据前面阈值法判定两种状态时,颗粒持续运动时间大于一个周期时才认为是处于连续状态,而前面间隔时间必大于一个崩塌周期时间。情况与Fischer的论文结果是一致的。

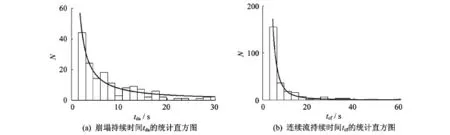
图4　崩塌与连续流各自持续时间的统计分布Fig.4　Distribution of time tdaand tcf

3.3CF出现时间在总测量时间所占比例随转速的变化

图5所示是滚筒颗粒在1.1～2.5（°）/s中,测量时间为600 s时,连续流持续时间总和占总的测量时间的百分比Φ的变化情况。由图知随着滚筒转速Ω的增大,滚筒中颗粒越来越长时间的保持连续状态,在1.493（°）/s转速时,Φ由0变为0.055 9,颗粒运动开始出现连续流；在1.92（°）/s时,Φ能够达到0.626 9；在2.240（°）/s转速时Φ达到最大值1。利用最小二乘法拟合得到Φ与滚筒转速Ω有反正切函数关系,特征系数为4.583、—8.46。

综上从三个角度得出的结论跟Fischer文献相一致,从而论证了DS方法测量的准确性。

3.4颗粒温度均值随转速的变化

由图6可以观察到颗粒温度均值、连续部分颗粒温度均值以及崩塌部分颗粒温度均值的变化趋势是相一致的；颗粒温度均值随着滚筒转速的增大先增大,之后当滚筒转速在1.8（°）/s到2（°）/s之间时,三个颗粒温度均值均降低；滚筒转速在2（°）/s以后崩塌部分的颗粒温度均值先增大,当滚筒颗粒运动全部进入到连续流以后崩塌消失；滚筒转速在2（°）/s以后连续流部分颗粒温度跟整体颗粒温度均值一起变大,并且两者差值减小,当全部进入连续流以后两者相同。

图5　连续状态持续时间占总测量时间的百分比Φ随转速Ω的变化Fig.5　The percentageΦchanges in the CF regime duration of the total measurement time with the speedΩ

图6　不同部分颗粒温度均值随滚筒转速的变化Fig.6　The temperature in different part with the change of the speed of the cylinder

3.5 过渡过程中DA峰值均值与CF峰值均值的比较

据图7可知在过渡状态时,崩塌将部分峰值均值与连续流部分峰值均值随滚筒转速的变化趋势相一致,一开始一致变大,并且都在1.6（°）/s处一起达到最大,然后颗粒温度逐渐减小,滚筒转速在1.9（°）/s时,两颗粒温度均保持平稳状态,不再有较大波动。根据各数值的误差棒可以看出只是在2.133（°）/s转速时连续流部分颗粒温度有一个较大的波动,而整体颗粒温度数值波动不大。

3.6概率统计角度阐述过渡过程

图8所示为滚筒转速在1.493（°）/s,测量时间600 s下,测量出在崩塌时的间隔时间tr,绘制统计直方图并对直方图做了高斯拟合。

图7　所有崩塌部分峰值的均值和连续部分峰值的均值随滚筒转速的变化以及各自误差棒Fig.7　Mean DA peaks and mean CF peaks with the change of the roller speed and the respective error bar

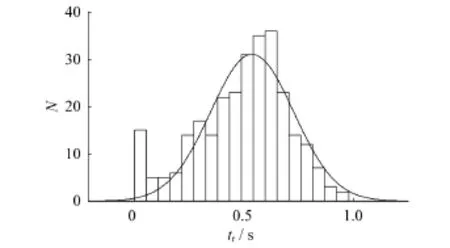
图8　间隔时间tr统计直方图及其高斯拟合Fig.8　Statistical histogram of interval time trand Gauss fitting

据图8可知,在1.493（°）/s滚筒转速下,崩塌间隔时间的统计分布呈现相对标准的高斯分布,利用最小二乘法拟合得到tr统计直方图为高斯函数,拟合特征系数为31.080 0、0.538 1、0.269 0。tr的均值为0.538 1,方差为0.190 3,均值减去三倍方差为—0.032 7,小于0。说明此转速下有连续流情况出现,结果与图6中显示1.387（°）/s转速下,滚筒颗粒运动开始有连续流出现相一致。

图9所示是滚筒颗粒在1.1～2.5（°）/s转速下,崩塌间隔时间tr均值的变化,误差棒长度为3倍标准差,拟合曲线如图所示。

可以看出,崩塌间隔时间均值随着滚筒转速变大而减小。崩塌间隔时间均值为0,表示颗粒运动进入连续流状态。根据高斯分布函数可知,约99.7%数值分布在距离平均值有3个标准差之内的范围。从图中可以看到当滚筒转速为1.493（°）/s时,误差棒已经接触到纵坐标0的位置,说明此时已经有连续流状态出现,与前面图4相一致。在崩塌间隔时间的拟合中是包含了0点,而0点则意味着连续流,所以其拟合曲线超过0点的含义就是,在此转速下有连续流出现,这个结论跟前面图5、图6也相一致。

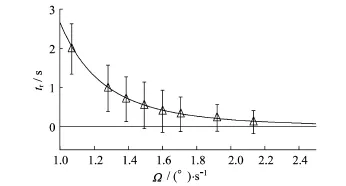
图9　间隔时间tr均值随滚筒转速的变化及其拟合曲线Fig.9　The change of trmean of the interval time. The change of the roller speedΩand the fitting curve

4　结 论

滚筒转速在1.4～2.3（°）/s之间时,滚筒内颗粒运动同时存在崩塌状态和连续状态,处在过渡状态。在此过程中,连续状态存在时间会逐渐变大,一直到全部为连续状态,并且滚筒内颗粒温度随着滚筒转速提高,先增大后减小,然后再增大,中间存在波动。另外,从概率统计角度来看,过渡过程的出现,是因为在特定转速范围内,崩塌间隔时间有过零部分,并随转速变大,过零的比例越大,而在零点则表示颗粒运动状态为连续运动状态。

［1］ HERRMANNH J.Grainsofunderstanding［J］.Physics World,1997,10（11）:31-34.

［2］ BRIDGEWATERJ.Particletechnology［J］.Chemical Engineer Science,1995,50（24）:4081-4089.

［3］ 鲍德松,张训生.颗粒物质与颗粒流［J］.浙江大学学报:理学版,2003,30（5）:514-517.

［4］ 叶坚,毛旭锋,夏建新.颗粒流研究最新进展与挑战［J］.中央民族大学学报:自然科学版,2009,18（4）:26-35.

［5］ RAJCHENBACH J.Flow in powders:From discrete avalanches to continuous regime［J］.Physical Review Letters,1990,65（18）: 2221-2224.

［6］ FISCHER R,GONDRET P,RABAUD M.Transition by intermittency in granular matter:From discontinuous avalanches to continuous flow［J］.Physical Review Letters,2009,103（12）:128002-1-4.

［7］ BENZA V G,NORI F,PLA O.Mean-field theory of sandpile avalanches:From the intermittent-to the continuous-flow regime［J］. Physical Review E,1993,48（5）:4095-4098.

［8］ BANDYOPADHYAY R,GITTINGS A S,SUH SS,et al.Speckle-visibility spectroscopy:A tool to study time-varying dynamics［J］. Reviewof Scientific Instruments,2005,76（9）:093110.

［9］ KATSURAGI H,ABATE A R,DURIAN D J.Jamming and growth of dynamical heterogeneities versus depth for granularheap flow［J］.Soft Matter,2010,6（13）:3023-3029.

［10］ MERRER M L,COHEN-ADDAD S,HÖHLER R.Bubble rearrangement duration in foams near the jamming point［J］.Physical Review Letters,2012,108（18）:188301.

［11］ 宋磊磊,孔平,于小强,等.一种用于研究激光散斑血流成像方法的测试系统［J］.光学仪器,2015,37（2）:107-115.

［12］ 孔平,杨晖,林伟民,等.动态散斑对比度颗粒测量法［J］.光学精密工程,2014,22（10）:2633-2638.

［13］ GOODMAN J W.Statistical optics［M］.New York:Wiley-Interscience Press,2000:320-390.

（编辑:张 磊）

Study on the mechanism of the pattern transition of granular flow based on the technique dynamic speckle

MA Sheng1,YANG Hui1,LI Ran1,SHENG Xubo1,ZHENG Gang2,WANG Shihao1,YAO Xin1
（1.School of Optical-Electronical and Computer Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China；2.School of Medical Instrument and Food Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China）

The research on the transformation of granular flow pattern has important theoretical and practical significance.This paper takes the granular flow in rotating drum as the research object,and uses the method of dynamic speckle（DS）measurement to study the transformation mechanism between the 2 modes of avalanches pattern and continuous flow pattern.The measurement of DS is used to study the transition phenomenon,and try to explain the mechanism of the transition from the two state duration probability distribution.The images of dynamic laser speckled by the CCD camera are obtained,and then the relationship between the moving velocity and time was figured out by the analysis of the contrast of dynamic laser speckle.The duration of discrete avalanches regime and continuous flow regime,duration of avalanche and avalanche interval were studied.By analyzing the statistical distribution of curve fitting,using the statistical results of the preceding,the characteristics are obtained.Results show that the two kinds of state transition is not mutation,but there is coexistence of the two states of the transition state,and follows their own existence probability becoming big or smalland gradually stabilized.

granular flow；avalanches pattern；continuous flow；transition regime；dynamic speckle

O 436

A

10.3969/j.issn.1005-5630.2016.02.013

1005-5630（2016）02-0159-08

2015-09-08

国家自然科学基金（11572201）

马 生（1989—）,男,硕士研究生,主要从事测试系统和颗粒技术研究。E-mail:masheng302@126.com

杨 晖（1981—）,男,副教授,主要从事颗粒技术研究。E-mail:yanghui313@126.com