对“基于改进广义cat映射的彩色卫星图像加密算法”的安全性分析

马俊明，叶瑞松（汕头大学数学系　广东　汕头　515063）

对“基于改进广义cat映射的彩色卫星图像加密算法”的安全性分析

马俊明，叶瑞松
（汕头大学数学系广东汕头515063）

对一种基于改进广义cat映射的彩色卫星图像加密算法进行安全性分析，并提出相应的选择明文/密文攻击和已知明文攻击方法.该算法改造了一般广义cat映射，通过增加一个非线性项使得一般广义cat映射具有更好的混沌特性；并利用改进广义cat映射进行图像置乱，然后用复合混沌映射对置乱后的图像进行扩散运算，实现图像加密.经过理论分析发现该算法存在两方面不足.一方面是扩散过程过于简单，采用简单的整幅图像的异或运算；另一方面是采用改进广义cat的置乱过程与明文无关.这两方面的不足，使得算法很容易受到破译.理论和仿真实验均表明该算法无法抵抗选择明文/密文攻击和已知明文攻击.关键词混沌映射；图像加密；选择明文攻击；选择密文攻击；已知明文攻击

0　引言

由于图像具有信息表达直观、信息量大、相邻像素的相关性强、冗余度大及其视觉属性等特点，使得传统的对文本信息而设计的加密算法，如DES，IDEA，RSA，已经不再适应图像信息加密的应用场合［1］.为了图像信息安全的应用需要，很多信息安全研究的学者提出了各种各样的加密新算法，其中基于混沌的图像加密算法独占鳌头，是目前图像加密研究中最热门的研究课题.混沌映射具有初值和系统参数的高度敏感性、混沌序列伪随机性、轨道遍历性以及不可预测性等复杂特性，因此混沌映射非常适合用于加密系统的置乱和扩散［3］.

一般来说，研究者在设计基于混沌图像加密算法时主要使用四种策略.第一种也是最容易实现的策略就是利用混沌映射产生的序列掩盖图像像素值［4］.第二种策略一般称为置乱，即利用混沌映射产生的混沌序列量化生成相应的置乱变换，从而改变图像像素位置而实现加密［5］.第三种策略依赖于混沌映射的迭代次数，这类策略中经常被提起的是Baptista型加密算法［6-7］.第四种策略是将混沌映射和明文图像联系起来，生成加密过程的密钥流，通常表现为前三种策略的交叉结合.显然第四种策略的安全性会比前三种高，但也不一定是安全不可破解的.文献［8］提出的图像加密算法充分体现了第四种策略，但发表不久后就被王兴元等人运用选择明文攻击成功实现了破译［9］.实际上，目前图像加密算法中有很多是基于混沌系统的图像加密算法，但是对基于混沌的图像加密的密码学理论并未完善.基于混沌系统的图像加密算法有待进一步做理论上的研究分析，特别对该类加密算法的密码学分析很有必要，也很有价值，有助于提高该类算法的安全性、实用性.一些学者陆续发现了基于混沌的图像加密方案所存在的缺陷，一些基于混沌系统以及置换-扩散结构的图像加密算法已经陆续遭到破译［10-15］.这些遭遇破解的加密算法中大部分有这样一个特征，就是置换过程和扩散过程是相互独立的，置换过程的密钥流与明文图像无关，而扩散过程的密钥流虽然与图像相关，但是扩散函数设计安全性有缺陷，从而使得选择明文攻击、已知明文攻击等密码分析得以实现.

最近，一种基于改进广义cat映射的图像加密算法由张新和柏逢明提出［16］.该算法对一般广义cat映射增加了非线性项，使得一般的广义cat映射具有更好的混沌特性；并利用改进广义cat映射进行明文图像的置乱，然后用复合混沌映射对置乱后的图像进行扩散运算，实现图像加密，达到较好的加密效果.本文将对文献［16］所构造的加密算法进行安全性分析.通过分析，发现文献［16］的加密算法的置乱过程与扩散过程相互独立，并且置乱过程和扩散过程均过于简单.扩散过程采用简单的整幅图像的异或运算；置乱过程虽然采用改进广义cat映射，但是与明文无关.这两方面的不足，使得算法很容易受到破译，无法抵抗选择明文/密文攻击以及已知明文攻击.在已知明文攻击分析中，还发现该算法提出的改进cat映射虽然增加非线性项，但是在安全性方面并没有提高.安全性理论分析结果表明该算法无法抵抗选择明文攻击、选择密文攻击及已知明文攻击，仿真模拟结果也证实了，在不知道密钥的情况下，可以对任意一幅密文图像进行完整的破译.

1　基于改进广义cat映射的彩色卫星图像加密算法

文献［16］的加密算法包括两部分.首先利用改进广义cat映射对彩色明文图像的三个色彩分量分别进行置乱.然后，利用复合混沌映射对置乱后的图像进行扩散得到密文图像.虽然加密算法是针对卫星图像，但是用其它一般的图像所做的破译分析，一样对卫星图像的破译有效.该算法的具体操作步骤如下.

1.1置乱过程

彩色明文图像可以用三维矩阵P表示，假设矩阵大小为N×N×3.在置乱过程中，改进广义cat映射被用来置乱图像：

其中（x，y），（x′，y′）分别为置乱前后像素坐标，f（x′）=x′2.

Step 1.给定复合混沌映射（简称CCM）：

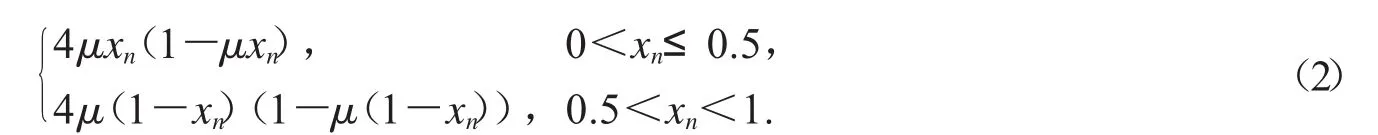
假设用于置乱彩色图像三个颜色分量的三个映射的参数分别为μ1，μ2，μ3，初始值分别为x1，x2，x3.

Step 2.分别迭代CCM共N×N+d次，得到对应序列I1，I2和I3，其中d为给定正整数，属于加密密钥的一部分，其作用是扔掉混沌序列的前d个过渡点，提高序列的混沌特性.

Step 3.利用下述公式生成改进广义cat映射的控制参数：

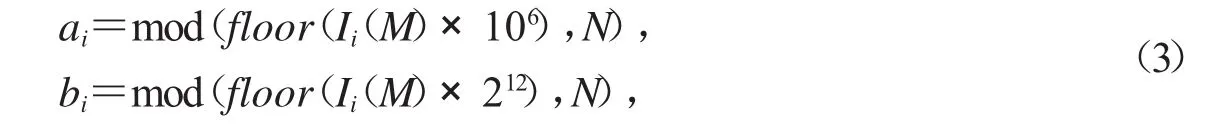
其中i=1，2，3，M可视为密钥之一.

Step 4.利用（1）和（3）对彩色图像P的三个色彩分量分别进行置乱，得到置乱图像CR，CG，CB.

1.2扩散过程

Step 1.分别取序列I1，I2和I3的后面N×N个序列值，构成序列Y1，Y2和Y3，如式（4）所示：

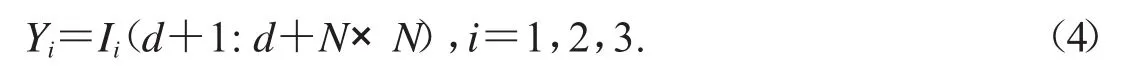
Step 2.由式（5）生成扩散过程的伪随机密钥流Ki：

Step 3.将密钥流Ki从上到下，从左到右依次进行排列，得到三个N×N矩阵Xi.置乱图像通过矩阵Xi进行扩散加密，得到密文图像的三个分量矩阵：

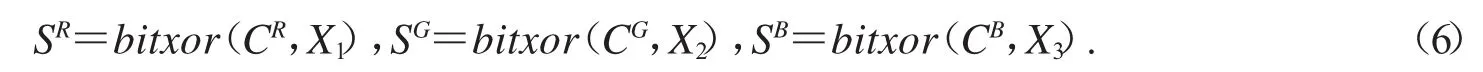
将矩阵SR，SG，SB进行色彩合成得到彩色加密图像S.这里也可以先将Xi进行色彩合成X，然后通过S=bitxor（C，X）生成加密图像，其中C为彩色置乱图像.后面的写法是为了行文方便，两者完全等价.

解密算法和加密算法类似.对于密文图像，首先使用与加密时相同的密钥流矩阵执行扩散过程的逆过程，然后对反扩散后的图像矩阵进行反置乱，即可得到原始明文图像.正如文献［16］所说，CCM的初始值、映射参数，M和d构成加密算法的全部密钥，更多具体细节可以参考该文献.

2　密码学分析

密码分析学的主要任务是研究密码破译的理论和技术.根据Kerchoff原则［1］，一般假设分析者在分析加密算法时能准确地知道这个加密系统的设计和运作，充分了解加密和解密算法，但不知道加密者使用的密钥.本文主要涉及选择明文攻击、选择密文攻击和已知明文攻击，具体介绍如下：

（A）选择明文攻击：分析者拥有有利于破解算法的选择明文及其对应密文；

（B）选择密文攻击：分析者拥有有利于破解算法的选择密文及其对应明文；

（C）已知明文攻击：分析者拥有足够多使用同一密钥加密的密文及其对应明文.

2.1选择明文攻击

首先选择像素值全为零的明文图像P1加密得到对应密文图像S1.由于置乱过程中只改变像素点坐标而不改变像素值，故P1置乱后仍为P1.根据式（6）可得：

S1=bitxor（P1，X）=bitxor（O，X）=X，

其中O为全零矩阵.然后选择第二幅明文图像P2进行加密得到S2.P2的三个色彩分量都是由序列1到N×N从上到下从左到右依次排列成N×N矩阵，具体如下：

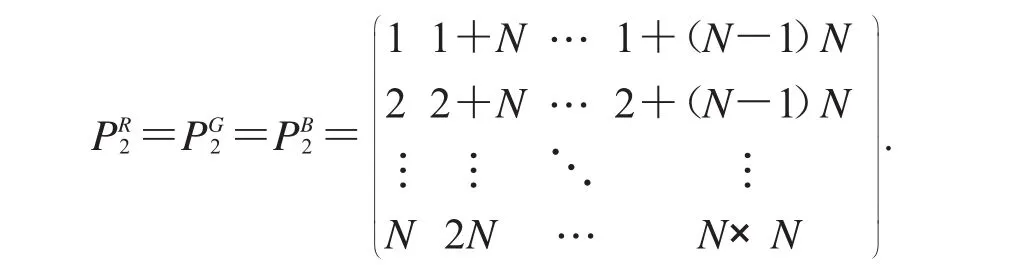
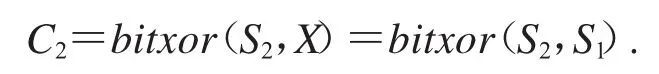
由式（6）可知P2置乱后的图像C2为 C2对于破解置乱过程起到关键性作用，因为C2中每一像素点的像素值都可以表示该像素点置乱前坐标，即C2（x′，y′）=x+（y-1）N=P2（x，y）.

假设待破译密文图像为S，利用上述得到的两幅图像S1和C2进行破译如下：

Step 1.利用式（6）以及S1得到S对应的置乱图像C：

Step 2.设明图像为P.将图像C，C2，P不同色彩分量从上到下从左到右依次转化成长度为N×N的序列CIR，C2IR，PIR，CIG，C2IG，PIG，CIB，C2IB，PIB，执行运算

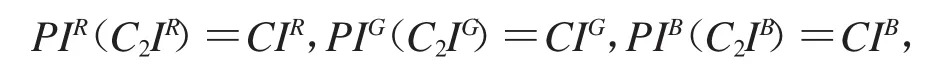
这里将图像分成三个分量来处理主要是方便使用Matlab编程实现，上式也可以用P（C2）=C代替.

Step 3.将序列PIR，PIG，PIB恢复成矩阵形式并合成明文图像P.

2.2选择密文攻击

选择密文攻击和选择明文攻击类似，但操作步骤有所不同，下面将具体描述选择密文攻击.取2.1中两幅明文图像作为选择密文攻击中的选择密文图像S3=P1，S4=P2.设其对应的明文图像以及置乱图像分别为P3，P4，C3，C4.令dS=bitxor（S3，S4），dC=bitxor（C3，C4），dP=bitxor（P3，P4），由式（6）及定义可知：

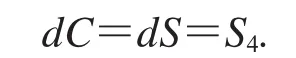
从dP到dC只经历置乱过程，dC每个色彩分量由序列1到N×N从上到下从左到右依次排列成N×N矩阵，易知dP像素值表示其置乱后坐标.注意dP与2.1节的C2有所不同，后者是正向置乱，前者是反向置乱.根据标准置乱图像以及P3可以求出C3，C3（dP）=P3.又由式（6）及S3定义可知C3=X.

假设待破译密文图像为S.求解对应置乱图像C，C=bitxor（S，C3），然后求解对应明文图像为P，P=C（dP）.至此完成选择密文攻击.

由于该加密算法的扩散过程过于简单，只使用了简单的异或运算，使得分析者容易利用特殊的明文或密文消除扩散效应得到只经过置乱过程的密文图像，这样的图像是非常容易受到暴力攻击的.论文在选择明文/密文攻击中只选取了两幅图像，在仿真试验中容易实现且运行时间短.综上所述，任意一个加密算法过于脆弱的扩散过程会使置乱过程失效并威胁到整个加密系统的安全性.

2.3已知明文攻击

虽然文献［16］在广义cat映射第二个变换表达式中添加了非线性项，但该非线性项只与第一个变换表达式有关，且第一个变换表达式的结果也会呈现在加密结果中，所以下面将运用同余函数性质来消除该非线性项.

假设点坐标（x，y）经过文献［16］中改进广义cat映射得到（x′，y′），满足式（1），而经过一般广义cat映射得到点（x″，y″），满足

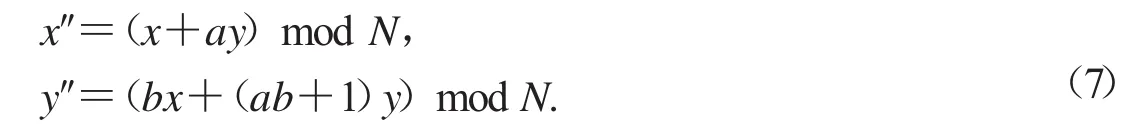
结合上式与（1）式可得

因此破译该算法的置乱过程只需要破解原始cat映射的控制参数a和b即可.

2.3.1求解含有控制参数a和b的矩阵M

由于文献［16］的加密算法对明文图像的不同色彩分量分别进行加密，所以此处不妨假设明文密文图像都是二维矩阵.假设已知明文-密文图像对（PA，SA），（PB，SB），对应置乱图像CA，CB.定义

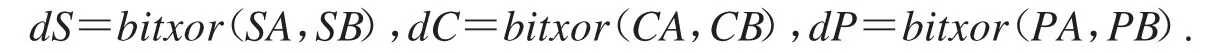
根据2.2节可知dC=dS且从dP到dC只经历置乱过程.将式（8）应用到dC可得由dP经过原始cat映射置乱后图像dC′.

不妨设dP（x1，y1）=v1，dP（x2，y2）=v2且v1≠v2.由式（7）可得

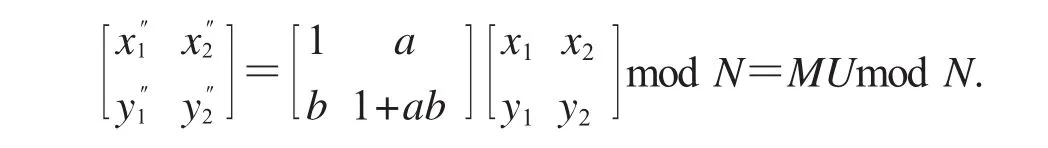
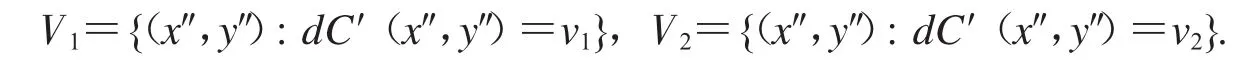
将dC′中像素值等于v1和v2的像素点构造成集合V1和V2：易知（x″1，y″1）∈V1，（x″2，y″2）∈V2.假设U可逆，定义集合V为

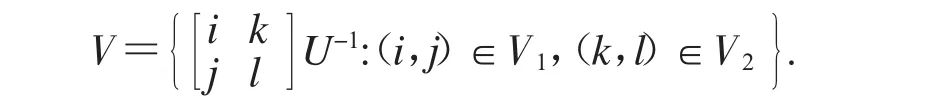
2.3.2破译密文图像

Step 1：利用矩阵M，式子（1），（7）和（8）可以得到PA的置乱图像CA；

Step 2：由式（6）可知SA=bitxor（CA，X）⇒X=bitxor（CA，SA）；

Step 3：利用待破译密文图像S求解对应置乱图像C=bitxor（S，X）；

Step 4：利用矩阵M，式（1），（7）和（8）求解对应明文图像为P.

3　仿真实验

仿真实验是指在一定的计算机条件下用仿真软件编程达到模拟现实的效果.大小为256×256的8比特经典测试彩色图像Lena将在软件Matlab R2014b下进行仿真.加密算法密钥取自文献［16］本身，即

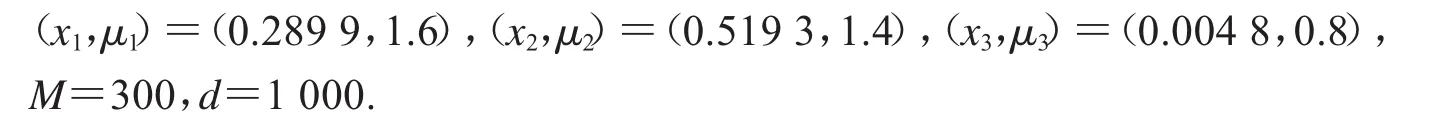
Lena明文图像以及相应的密文图像如图1所示.

图1　文献［16］的加密算法的加密结果

在对图像Lena进行破译之前，作为示例，先利用两幅8×8图像作为选择明文进行选择明文攻击，得到的数值过程如下.

Step1：由2.1可知两幅选择明文分别为

Step2：求解扩散过程中密钥矩阵X：

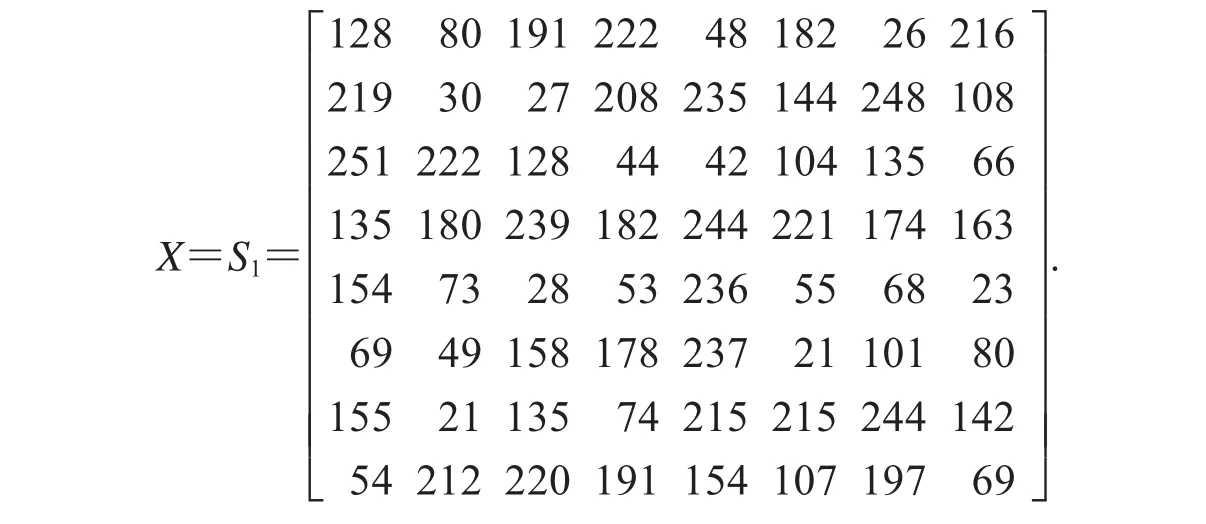
Step3：求解矩阵C2用于破解置乱过程：

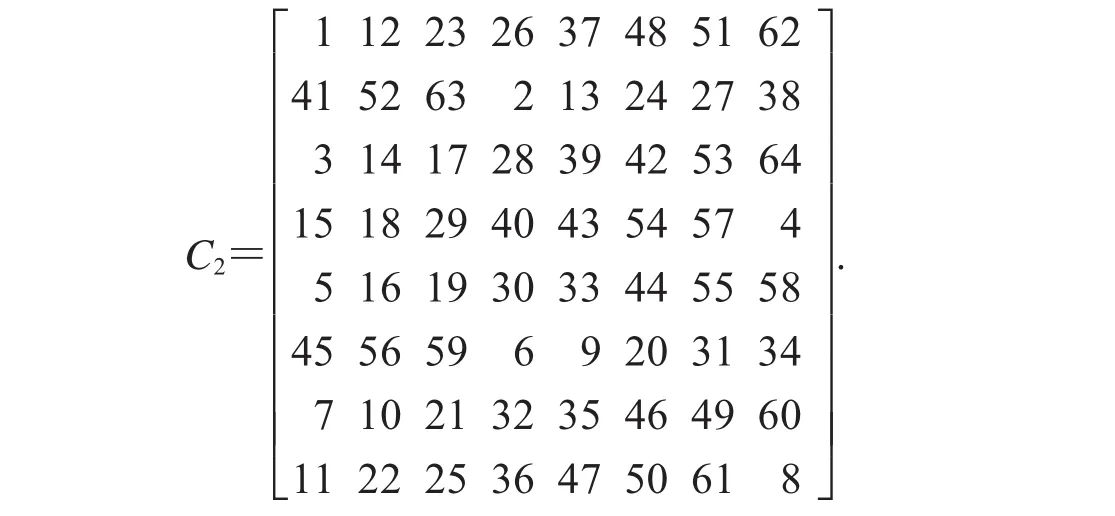
可以看出矩阵C2中并无重复的像素值，且每一个像素值都可以代表该像素点置乱前的位置.利用矩阵C2和X可以很好得还原任意一副8×8密文图像.对于图像Lena的仿真结果具体如图2和图3所示.

图2　（a）选择明文/密文Ⅰ，（b）选择明文/密文Ⅱ，（c）还原图像.

图3　（a）已知明文Ⅰ，（b）已知明文Ⅱ，（c）还原图像.

4　总结

论文对文献［16］的加密算法进行安全性分析并提出相应的选择明文/密文攻击和已知明文攻击分析.论文经过分析发现该加密算法主要存在两方面的缺陷.一方面是扩散过程过于简单，可以设计更安全的扩散函数改进扩散过程.另一方面是文献［16］提出的改进的广义cat映射混沌映射和一般广义cat映射可以相互转换，因而不能提高算法安全性，设计者可以考虑设计一个与明文图像相关的置乱过程，使得加密算法对不同的明文图像具有不同的密钥，从而更好的抵抗分析者的攻击，这也是后续的主要研究工作.

［1］STINSON D R.Cryptography：theory and practice［M］.Boca Raton：CRC Press，1995.

［2］MATTHEWSR.On the derivation ofa chaotic encryption algorithm［J］.Cryptologia，1989，13（1）：29-42.

［3］SHANNON C E.Communication theory ofsecrecy system［J］.Bell Syst Tech J，1949，28（4）：656-715.

［4］GAO H，ZHANG Y，LIANG S，et al.A newchaotic algorithm for image encryption［J］.Chaos，Solitons& Fractals，2006，29（2）：393-399.

［5］CHUNG K L，CHANG L C.Large encrypting binary images with higher security［J］.Pattern Recognition Letters，1998，19（5/6）：461-468.

［6］BAPTISTA MS.Cryptography with chaos［J］.Phys Lett A，1998，240（1/2）：50-54.

［7］葛辛.数字混沌加密技术研究［D］.河南：解放军信息工程大学，2007：1-9.

［8］ZHANG G，LIU Q.A novel image encryption method based on total shuffling scheme［J］.Optics Communications，2011，284（12）：2775-2780.

［9］WANG X，HE G.Cryptanalysis on a novel image encryption method based on total shuffling scheme［J］. Optics Communications，2011，284（24）：5804-5807.

［10］RHOUMA R，BELGHIT S.Cryptanalysis of a new image encryption algorithm based on hyper-chaos［J］. Physics Letters A，2008，372（38）：5973-5978.

［11］WANG Y，WONG K W，LIAO X F，et al.A chaos-based image encryption algorithm with variable control parameters［J］.Chaos，Solitons and Fractals，2009，41（4）：1773-1783.

［12］LI S J，LI C Q，CHEN G R，et al.A general quantitative cryptanalysis of permutation-only multimedia ciphers against plain-image attacks［J］.Signal Process：Image Commun，2009，23（3）：212-223.

［13］Li C Q，Li S J，Chen G R，Chen G，Hu L.Cryptanalysis of a newsignal security system for multimedia data transmission［J］.EURASIP J Appl Signal Process，2005，2005：1277-1288.

［14］叶瑞松，马俊明，曾少君.一种图像加密算法的密码分析及其改进［J］.汕头大学学报（自然科学版），2015，30（4）：57-70.

［15］马俊明，叶瑞松.一种图像加密算法的密码学分析［J］.网络新媒体，2015，4（6）：37-42.

［16］张新，柏逢明.基于改进广义cat映射的彩色卫星图像加密算法［J］.长春理工大学学报（自然科学版），2015，38（14）：93-96.

AbstractAcolor satellite image encryption algorithmbased on improved generalized cat mapping was proposed recently.The algorithmmodified the generalized cat mappingbyaddinga nonlinearterm to make the generalized cat mapping with more chaotic natures.Three color components of color images were scrambled by using the improved generalized cat mapping.The diffusion for scrambled image is carried out by using compound chaos mapping.In this paper，three kinds of cryptanalysis on this image encryption algorithm are devised，including chosen plaintext attack，chosen ciphertext attack and known plaintext attack.There are twoshortcomings in this encryption algorithm according to the theoretical security analysis.The diffusion processing only uses a simple XOR operation on the whole image.The scrambled image is independent on the plain image.Both theoretical and simulation experiments show that the encryption algorithm cannot resist chosen plaintext/ciphertext attacks and known-plaintext attacks.

Keywordschaotic mapping；image encryption；chosen plaintext attack；chosen ciphertext attack；known plaintext attacks

Security Analysis on a Color Satellite Image Encryption Algorithm Based on Improved Generalized Cat Mapping

MA Junming，YE Ruisong
（Department of Mathematics，Shantou University，Shantou 515063，Guangdong，China）

A

1001-4217（2016）02-0050-09

2015-12-08

叶瑞松（1968—），男（汉族），博士，教授.研究方向：分形混沌及应用.E-mail：rsye@stu.edu.cn

国家自然科学基金资助项目（11271238）