DV-Hop算法中未知节点获取校正值的改进方法

狄振强，马淑丽，赵建平，刘凤霞

(曲阜师范大学 物理工程学院,山东 曲阜 273165)



DV-Hop算法中未知节点获取校正值的改进方法

国家自然科学基金资助项目(No.11404185)；山东省高等学校科技计划项目资助(No.J12LN08)；曲阜师范大学技术开发项目(No.hxkj2015017)Foundation Item:National Natural Science Foundation of China(No.11404185); Supported by the Science and Technology Project of Higher Education of Shandong Province(No.J12LN08); Qufu Normal University Technology Development Project(No.hxkj2015017)

狄振强，马淑丽，赵建平，刘凤霞

(曲阜师范大学 物理工程学院,山东 曲阜 273165)

无线传感器网络中，大量传感器节点随机部署。在DV-Hop定位算法中，未知节点根据校正值和与锚节点间的最小跳数值估算自身与锚节点间的距离。校正值的选择和计算方法有多种。对比多种取校正值的方法，并提出两种新的计算校正值方法。MATLAB仿真表明，各种取校正值的方法在一定的通信半径下各占优势。新的计算校正值方法在相同条件下比其他方法明显占优势。改进的DV-Hop算法比一般的DV-Hop算法、加权的DV-Hop算法、最佳指数值下DV-Hop算法定位精度分别提高2.38%、1.96%、1.31%，同时不会增加网络硬件成本。

无线传感器网络;节点定位;加权DV-Hop算法;最小均方差

0　引　言

无线传感器网络(WSN, Wireless Sensor Network) 主要由大量传感器节点组成，可以应用于环境监测、精准农业、军事等领域。一般，在比较偏僻、无人值守的网络环境中，大量节点随机抛撒部署。由于成本等原因，少数节点已知自己的坐标，被称为信标节点或锚节点。剩余的大部分节点需要依靠网络中的锚节点估算自身坐标，这部分节点称为未知节点。在定位技术中，无需测距的定位算法由于简单、成本低受到广泛关注[1]。其中，国内外研究较多的是DV-Hop算法、APIT(Approximate Point-In-Triangulation Test)算法及衍生的算法等。由于无需测距定位算法定位精度不高[2]，许多学者通过改进算法来提高定位精度。关于改进DV-Hop算法的文献很多，大多是改进锚节点部署策略、改进最小二乘法、改进锚节点平均每一跳距离计算、改进定位条件等方面[3]。本文从校正值的计算和选择方面入手，改进DV-Hop算法。首先，列举并对比其他文献提出的一系列改进未知节点选择和计算校正值的方法。然后，提出两种新的未知节点获取校正值方法。最后，进行实验仿真对比。经实验证明改进的方法能提高DV-Hop算法定位精度。

本文的结构安排，第一部分，基本概述，包括DV-Hop算法及其定位误差分析。第二部分，列举了一些文献提出的未知节点选取和计算校正值的方法。第三部分，提出本文两种创新方法。第四部分，实验仿真，验证本文提出的新的方法的有效性。最后一部分，总结。

1　基本概念

1.1DV-Hop定位算法

Dragos Niculescu(美国罗格斯大学，Rutgers University)等人在2003年提出了6种分布式定位算法，其中包括DV-Hop定位算法[4]。

在无线传感器网络中，DV-Hop算法定位步骤如下：

(1)网络中的锚节点以泛洪的方式向周围广播包含自身坐标和初始跳数值0的数据包。接收节点保存数据包，将跳数值自加1后转发数据包出去。在不断的转发过程中，接收节点只保留跳数值较小的数据包，遇到比自己保留的跳数值大的数据包则抛弃。

(2)计算锚节点平均每一跳距离。锚节点将自己的平均每一跳距离值广播出去。

(3)未知节点选择性的接收广播信息并作为自己的平均每一跳距离(我们将未知节点选择的平均每一跳距离称为校正值)。用校正值乘以未知节点与每个锚节点间的最小跳数值，得到未知节点与每个锚节点间的估算距离。

最后，当未知节点获得与至少三个锚节点的距离时，可以用三边测量法[5]、极大似然估计法等估算坐标。

极大似然估计法：

(1)

AX=b

(2)

(3)

(4)

X=(ATA)-1ATb

(5)

(x,y)为未知节点坐标，di为未知节点与锚节点i间的估算距离。

1.2误差分析

基于无需测距的定位算法比基于测距的定位算法定位精度低，最主要的原因：基于测距的定位算法能够获得节点间较为精确的距离或角度信息，而无需测距的定位算法只能估算节点间的距离等信息。

如DV-Hop算法的第二至第三步，未知节点获取校正值，并将校正值乘以最小跳数值得到与锚节点间的距离。只是利用锚节点的坐标信息和信息传输过程中记录的跳数值来估算距离，误差较大[6]。如图1所示，网络中节点部署是随机的，节点间的距离有大有小，而在信息传输过程中跳数值记录为1对应的实际跳段距离也是有大有小。未知节点用跳数值乘以校正值获得与锚节点间的估算距离，误差很大。所以，需要选择合适的校正值来减小估算距离误差，从而提高定位精度。

图1　网络结构

2　计算或选择校正值方法

校正值会影响未知节点与锚节点间估算距离的误差。所以为了提升DV-Hop算法定位精度，许多文献从DV-Hop算法的第二和第三步入手，提高节点定位精度。本文研究了许多文献，并总结了7种校正值获取和计算的方法。如下：

(1)最常用的获取校正值方法。

许多文献如文献[7]，在第二步，利用无偏估计准则求锚节点的平均每一跳距离(dHopi)。首先，锚节点i计算出自己与其他锚节点(如锚节点j)间的距离dij。无偏估计准则需要满足：

(6)

然后，将锚节点i与其他所有锚节点间的距离累加，除以与其它锚节点(如锚节点j)间的最小跳数值hij的累加值，得到锚节点i的平均每一跳距离dHopi，如式(7)：

(7)

式中，xi，yi是锚节点i坐标值，xj，yj是锚节点j坐标值。

就近原则获取校正值，是大多数文献采用的方法。在第三步，未知节点只接收最近的锚节点的平均每一跳距离信息，即只接受第一个送达的平均每一跳距离信息，并将其作为自己的校正值。

(2)文献[1，5，8，9]求锚节点的平均每一跳距离公式如式(7)。未知节点对所有锚节点的平均每一跳距离取平均值后作为自己的校正值，即网络中所有未知节点的校正值相同。公式如下：

(8)

n为网络中锚节点个数。

(3)文献[2，10]。未知节点根据每个锚节点与自己距离的远近影响校正值的大小。首先，未知节点获取所有锚节点的平均每一跳距离，公式如式(7)。然后对每个锚节点的平均每一跳距离进行加权。

如式(9)，对锚节点j的加权系数Mji：

(9)

对锚节点j的平均每一跳距离进行加权处理：

MDji=Mji×dHopj

(10)

式(10)中dHopj由式(7)计算而来。将每个锚节点加权处理后的平均每一跳距离累加，得到未知节点的校正值。未知节点i的校正值为：

(11)

未知节点i与锚节点f(f取1～n)的估算距离为：

dif=MJi×hif

(12)

(4)文献[11]。利用最小均方差准则，锚节点平均每一跳距离满足：

(13)

对上式求关于dHopi的偏导，并将等式取零，得到最小均方误差下的求dHopi公式：

(14)

未知节点只接收离自己最近的锚节点发过来的平均每一跳距离信息。

(5)文献[12]。首先，用最小均方差准则求锚节点平均每一跳距离，如式(14)。然后，未知节点接收所有锚节点广播的平均每一跳距离。在计算未知节点与锚节点间估算距离时，求到哪个锚节点的距离用哪个锚节点的平均每一跳距离，即在DV-Hop算法的第三步未知节点i与锚节点j的估算距离为：

(15)

(6)文献[13]，也就是本文作者的另一篇论文提出的创新方法。改进式(14)，提出最佳指数值概念，在最佳值下求锚节点平均每一跳距离。研究发现指数在取非2时，取1.9～2.0间的数时能提高定位精度。公式如下：

(16)

未知节点只接收离自己最近的锚节点发过来的平均每一跳距离信息

(7)文献[14]，也是本文作者的另一篇论文提出的创新方法。将文献[9，12]的算法结合，提出最佳指数值下的加权DV-Hop算法。首先，用最佳指数值下的最小均方差准则求锚节点平均每一跳距离，如式(16)。然后，未知节点接收保留所有锚节点广播来的平均每一跳距离。并按照文献[2,10]的方法对每个锚节点的平均每一跳距离进行加权处理。最后，未知节点将每个锚节点加权处理后的平均每一跳距离累加，得到自身校正值。

3　改进的计算或获取校正值方法

本文提出两种新的未知节点选择和计算校正值的方法。

3.1改进方法一

第一种方法：我们对比第二节中未知节点计算和选择校正值的方法，发现锚节点利用最小均方差准则计算平均每一跳距离时误差较小，锚节点用改进的计算式(16)求平均每一跳距离时误差进一步减小。在未知节点选择校正值时，就近原则选取校正值的方法定位误差较大，而采用所有锚节点的平均每一跳距离参与到校正值计算时，定位误差较小。

所以，本文尝试并提出将所有锚节点在文献[12]最佳指数值下求锚节点平均每一跳距离的平均值作为未知节点的校正值。公式如下：

(17)

经过多次实验仿真，发现本文提出的未知节点选取校正值的方法可以明显的提高定位精度。

3.2改进方法二

第二种方法：我们将所有的锚节点平均每一跳距离都参与到校正值的计算。在DV-Hop算法中，未知节点需要计算与所有锚节点间的距离，然后，才能用最小二乘法或者三边测量法计位置。我们在未知节点计算与某个锚节点间的距离时，用该锚节点的平均每一跳距离乘以该锚节点与该未知节点间的最小跳数值。也就是说，用求到谁的距离用谁的平均每一跳距离。锚节点平均每一跳距离的计算公式仍然用在最佳指数值下的公式(16)。

求未知节点i求与锚节点j间的距离时，公式如下：

(18)

经过实验仿真，发现本文第二种方法也能减小节点定位误差，提高DV-Hop算法定位精度。

4　实验仿真

将无线传感器网络区域假设为100 m×100 m的正方形，其中随机部署100个传感器节点，锚节点的覆盖率为9%，传感器节点的无线通信半径取22～45 m范围。将文献[9-14]提出的未知节点选择和计算校正值的7种方法和本文提出的两种方法对比，为了便于区分，将本文第一、二种方法分别用DV-Hop(A)、DV-Hop(B)表示，如图2所示。

(a)文献[9]

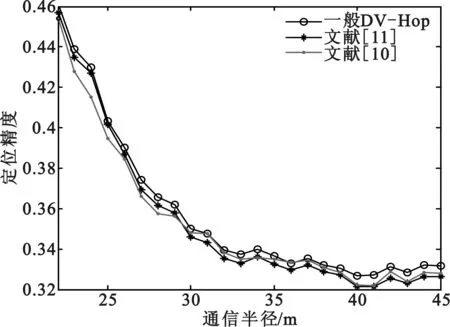
(b)文献[10-11]

(c)文献[11-12]

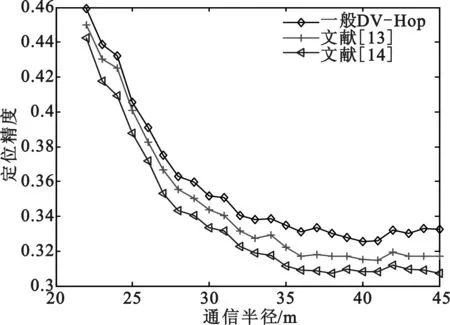
(d)文献[13-14]

(e)DV-Hop(A)

(f)DV-Hop(B)

经实验对比，如图2(a)、图2 (b)、图2 (c) 所示，文献[8-11]提出的未知节点选择和计算校正值的方法并不能明显的提高DV-Hop算法定位精度。如图2(d)所示，本文作者在文献[12-13]中提出的创新方法可以明显的提升定位精度。如图2(e)、图2(f)所示，本文作者在本文提出的两种新的未知节点选择和计算校正值的方法，可以在一定条件下比一般常用的方法大大的提高定位精度。本文第一种方法,用所有锚节点参与定位，即所有未知节点校正值相同，且每个锚节点的平均每一跳距离在最佳指数下计算时，定位精度比其他8种方法都占优势，如图2(e)所示。通信半径为35m时，本文两种方法分别比一般方法提高定位精度3%、2%左右。

5　结　语

无线传感器网络中无需测距定位算法的定位精度受限于未知节点的校正值和计算与锚节点间的估算距离。本文收集了一些未知节点校正值选择和计算的方法，并分别仿真对比。然后，提出两种新的未知节点校正值计算和选择方法。经过Matlab仿真证明，本文方法可以有效提高定位精度，总体上可以提升约3%的定位精度，换算到实际中可以将定位误差减小1 m左右。下一步，将研究基于多通信半径的定位算法，并将本文方法应用到其中。

[1]CHEN H, Sezaki K, DENG P, HC So. An Improved DV-Hop Localization Algorithm with Reduced Node Location Error for Wireless Sensor Networks. Ieice Transactions on Fundamentals of Electronics Communications & Computer Sciences. 2008, 91-a(8):2232-2236.

[2]YANG Xiao-ying, SONG Qi-xiang. An Improved DV-Hop Algorithm for Resisting Wormhole Attack. The Open Cybernetics & Systemics Journal,2015,9,1443-1448.

[3]DING J, ZHANG L,CHENG G, LING Z,ZHANG Z. Study on DV-Hop Algorithm based on Modifying Hop Count for Wireless Sensor Networks. International Journal of Computer Science Engineering & Technolo, Oct2012, Vol. 2 Issue 10, p1452.

[4]Niculescu D, Nath B. Ad-Hoc Positioning System(APS)[J].IEEE Global Telecommunications,2001,5:2926-2931.

[5]ZHANG Shu-peng. Wireless Sensor Network Positioning Technology Research [D] Guangzhou: South China University of Technology, 2010.

[6]YANG H, WANG Q, LIU Z. A Wireless Sensor Network DV-Hop Localization Algorithm. International Conference on Information Science & Computer Applications, 2013, 92:281-286.

[7]CHEN Xiao and ZHANG Ben-liang. Improved DV-Hop Node Localization Algorithm in Wireless Sensor Networks. International Journal of Distributed Sensor Networks, vol.2012, Article ID 213980, 7 pages, 2012.

[8]WU Hua-rui, GAO Rong-hua. An Improved Method of DV-Hop Localization Algorithm. Journal of Computational Information Systems 7:7(2011) 2293-2298.

[9]贾琦,周新志.基于无线传感器网DV-Hop定位算法的改进和研究[J]. 计算机测量与控制,2013，21(11): 3043-3046.

JIA Qi, ZHOU Xin-zhi. Improvement and Research on DV-Hop Localization Algorithm for Wireless Sensor Networks[J]. Chinese Journal of Computer Measurement & Control，2013.21(11):3043-3046.

[10]冯江,朱强,吴春春.改进的DV-Hop定位算法研究[J].计算机工程,2012,38(19):74-81.FENG Jiang, ZHU Qiang, WU Chun-chun. Research on Improved DV-Hop Localization Algorithm[J]. Chinese Journal of Computer Engineering,2012,38(19):74-81.

[11]魏全瑞,刘俊,韩九强.改进的无线传感器网络无偏距离估计与节点定位算法[J].西安交通大学学报,2014, 48(06):1-6.

WEI Quan-rui,LIU Jun,HAN Jiu-qiang. An Improved DV-Hop Node Localization Algorithm based on Unbiased Estimation for Wireless Sensor Networks[J]. Journal of Xi’an Jiaotong University,2014,48(06):1-6.

[12]嵇玮玮,刘中.DV-Hop定位算法在随机传感器网络中的应用研究[J].电子与信息学报,2008,30(04):970-974.

JI W W,LIU Z. Study on the Application of DV-Hop Localization Algorithms to Random Sensor Networks[J]. Chinese Journal of Electronics & Information Technology, 2008，30(04):970-974.

[13]马淑丽,赵建平.无线传感器网络中DV-Hop定位算法的改进[J]. 通信技术,2015,48(07):840-844.

MA S L,ZHAO J P,ZHANG B T. The Improvement of DV-Hop Algorithm in Wirless Sensor Networks[J]. Chinese Journal of Communications Technology, 2015,48(07):840-844.

[14]马淑丽,赵建平. WSN中基于最佳指数的加权DV-Hop算法[J].通信技术,2015,48 (10):1147-1151.

MA S L,ZHAO J P,ZHANG B T. Weighted DV-Hop Algorithm based on Optimal Index in WSN[J]. Chinese Journal of Communications Technology, 2015, 48(10):1147-115.

狄振强(1965—)，男，副教授，主要研究方向为无线通信技术、物联网技术；

马淑丽(1989—)，女，硕士研究生，主要研究方向为无线传感器网络、无线通信技术；

赵建平(1964—)，男，教授，主要研究方向为无线通信技术；

刘凤霞(1988—)，女，硕士研究生。主要研究方向为智能信息处理。

A Modified Method for Obtaining Correction Value of Unknown Nodes in DV-Hop Algorithm

DI Zhen-qiang，MA Shu-li，ZHAO Jian-ping，LIU Feng-xia

(College of Physics Engineering,Qufu Normal University,Qufu Shandong 273165,China)

In wireless sensor networks, a large number of nodes are randomly distributed. In DV-Hop localization algorithm, the unknown nodes estimate the distance between themselves and the anchor nodes in accordance with the corrected value and the minimum hop count between the anchor nodes. There are various method for selection and calculation of the correction value. After the comparison of multiple methods, two novel methods for calculating the correction value are proposed. MATLAB simulation indicates that various methods for obtaining correct values enjoy different advantages under a certain communication radius. The novel calculation method is clearly superior to other methods in same conditions. The positioning accuracy of modified DV-Hop algorithm is improved by 2.38%, 1.96%, 1.31% respectively as compared with that of DV-Hop algorithm, the weighted DV-Hop algorithm,and the DV-Hop algorithm of optimal index value,without any increase of network hardware cost.

wireless sensor network; node localization; weighted DV-Hop algorithm; minimum mean square error

10.3969/j.issn.1002-0802.2016.03.015

2015-10-11；

2016-01-26Received date:2015-10-11；Revised date：2016-01-26

TP393

A

1002-0802(2016)03-0329-06