基于多参数分数傅里叶变换和ARNOLD变换的图像加密方法

李　洋，王兆伟，徐山峰，张永利

(中国电子科学研究院，北京　100041)



工程与应用

基于多参数分数傅里叶变换和ARNOLD变换的图像加密方法

李洋，王兆伟，徐山峰，张永利

(中国电子科学研究院，北京100041)

利用多参数分数傅里叶变换(MPFRFT)对图像进行双随机相位加密，提供了更加丰富的密钥空间，使加密图像具有较高的安全特性。但是随机相位矩阵作为密钥占用了更多的密钥空间，给传输和解密都带来负担。本文提出将MPFRFT和ARNOLD变换相结合的加密方法，利用ARNOLD变换对给定相位矩阵进行置乱变换，再利用置乱矩阵对图像进行相位编码，然后利用MPFRFT变换进行图像加密。本文提出的加密方法不需要随机相位矩阵作为密钥随加密图像进行传输，节省了密钥空间。仿真实验表明该算法具有更小的密钥空间，同时仍然具有较高的安全特性和抗攻击能力。

多参数分数傅里叶变换(MPFRFT)； ARNOLD变换; 图像加密

TP309.7

A

1673-5692(2016)02-164-05

0　引　言

图像数据的获取、传输和处理已经成为人类接收和表达信息的重要手段。对于一些涉及到国家安全、商业机密或个人隐私的图像信息采取必要的安全保护措施是非常必要的，否则会带来严重的后果。图像加密技术是保护图像信息最直接、最有效的方法[1]，这种技术将图像数据处理成杂乱无章的、类似噪声的无意义图像，然后进行保密传输，加密的图像使未授权者无法浏览图像内容。

多参数分数阶傅里叶变换(MPFRFT)的提出源于分数阶傅里叶变换(FRFT)的多样性特征，是将加权类分数傅里叶变换推广到包含两个向量参数M,N∈M的一种广义定义形式[2-3]。利用MPFRFT对图像进行加密，加密密钥包括联合二维周期参数、联合二维分数阶数和联合二维向量参数等，扩大了加密图像的密钥空间，使得加密过程的安全性得到了较好的保证。但是利用MPFRFT对图像进行加密前，需要对图像进行随机相位编码，随机相位矩阵作为密钥与加密图像进行传输，占用了传输资源，给加密、传输带来安全性隐患和资源负担。ARNOLD变换是一种置乱变换[4]，其直接表现为将一副给定的数字图像变成一副杂乱无章的图像，图像要表达的真实信息无法直观地传送到未授权者。即使利用高效计算机对各种可能的像素组合情况进行复原计算，其花费的计算时间也是非常巨大的。

本文提出了基于MPFRFT和ARNOLD变换的图像加密方法。首先利用MPFRFT的向量参数进行ARNOLD变换产生随机相位矩阵，对图像进行随机相位编码。然后利用MPFRFT对相位编码图像进行加密。这样ARNOLD置乱映射密钥替代随机相位矩阵，节约了密钥空间，而安全性和抗攻击性没有降低。本文内容安排如下：第一节对MPFRFT进行简要的描述；第二节将给出广义ARNOLD变换和本文提出的加密算法；第三节对算法进行仿真验证，并进行仿真分析和结果讨论；第四节给出本文结论。

1　MPFRFT定义

MPFRFT概念源于分数傅里叶变换(FRFT)。MPFRFT是利用M周期加权的思想对FRFT的一种描述，而分数傅里叶变换是传统傅里叶变换(FT)的一种广义形式，因此MPFRFT既丰富了FRFT的来源多样性，也对传统FT进行了巧妙的内涵扩展，丰富了一维和二维信号处理的时频处理工具。下面给出一维和二维分数傅里叶变换和MPFRFT定义。

首先定义α阶分数傅里叶变换Fα如下[5]：

(1)

其中Kα(u,t)为分数傅里叶变换核：

(2)

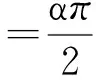
对图像进行加密本质上是对二维信号f(t,s)进行处理，所以αL,αR阶二维分数傅里叶变换FαL,αR定义如下[6]：

(3)

其中KαL,αR(u,v,t,s)为二阶分数傅里叶变换核：

(4)

二维信号f(t,s)的二维FRFT是线性的，满足阶数和角度的可加性、交换性、结合性等特征，二维FRFT的逆变换定义如下：

(u,v,t,s)dtds.

(5)

公式(5)表明对信号做二维FRFT后，要对信号进行复原只需进行相反阶数的第二次FRFT，就可以得到变换前的信号形式。

Shih在1995年利用态函数提出FRFT的一种新的定义形式，基本思想是利用经典的FT整数次幂运算的四周期特征，将FRFT定义为四个态函数作为加权系数的线性组合，加权系数是FRFT幂次的连续函数。经过研究人员的进一步研究，将Shih加权类FRFT推广到周期为任意整数(M≥2)的加权类FRFT[7]，其基本变换为：

(6)

(7)

其中

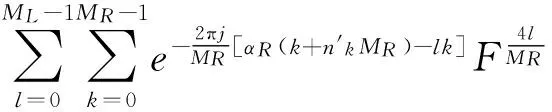
2　图像加密

ARNOLD变换实际是一种点的位置移动。设N阶数字图像矩阵上一点(x,y)，将点(x,y)变换到另一点(x′,y′)，定义如下[10]：

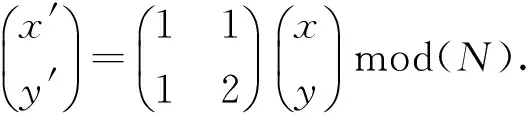
(8)

本文将MPFRFT和ARNOLD变换进行结合，提出基于一种基于MPFRFT和ARNOLD变换的图像加密算法。

设图像X=(xn,m)N×M，加密过程如下所示：

步骤一：利用MPFRFT变换向量参数NL=(n0,n1,…,nML-1)，按照一定规则得到矩阵β(n, m)。对矩阵β(n, m)进行ARNOLD变换得到矩阵β1(n, m), n∈[1,N], m∈[1,M]，对β1(n, m)进行再一次的ARNOLD变换得到矩阵β2(n, m), n∈[1,N], m∈[1,M]；

步骤二：利用矩阵β1(n, m)进行第一次相位编码得到X⊗ejβ1(n,m)；

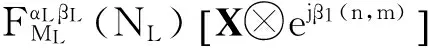
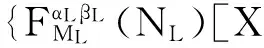
对于加密图像Q进行解密操作如下所示：

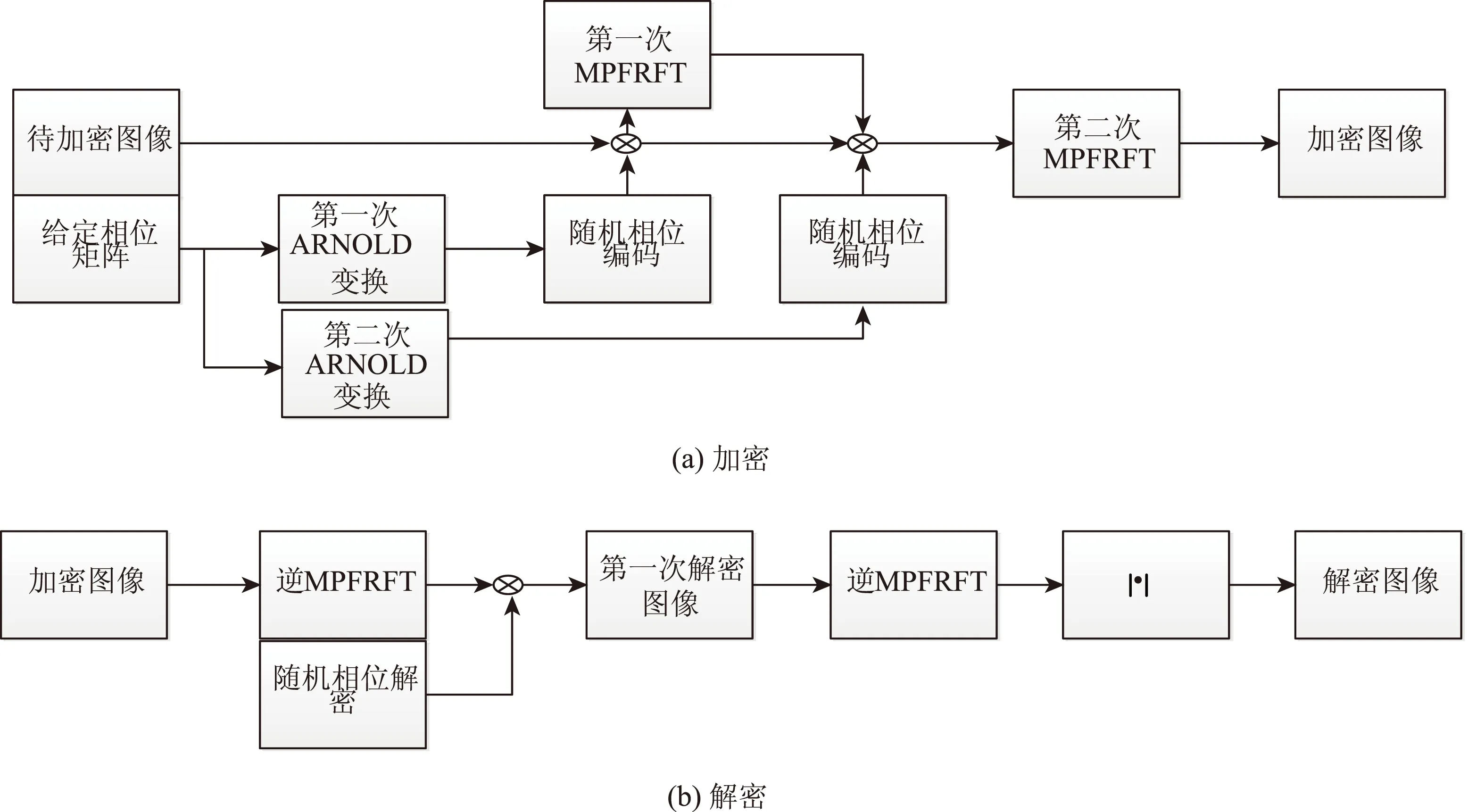
图1　加密解密流程图：(a)加密, (b)解密

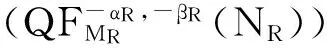
步骤四：取图像的幅度信息，得到解密图像。

步骤一关于矩阵β的选取此处我们采用如下方法：先随机选取向量参数NL=(n0,n1,…,nML-1)，其中ML-1等于加密图像的一个维度长度。然后将NL作为矩阵β的行向量依次排列，组成ML-1×MR-1矩阵β，其中MR-1为加密图像的另一个维度长度。

本文提出的基于MPFRFT和ARNOLD变换的图像加密、解密方法具体流程见图1所示。

3　仿真实验

为了验证本文算法的安全性和抗攻击性，对256×256像素的lena灰度图像进行加密和解密操作。两次MPFRFT的密钥分别为(0.6,1.2)和(0.3,1.5)。对图像进行加密，原图像、加密图像和解密图像在图2中分别给出。同时给出每种图像对应的直方图。从直方图中可以看出原图像和解密图像的灰度值主要集中在特定某些区域的灰度值，但是加密文件直方图的灰度失去了这种特性，主要集中在中部，失去原有的灰度规律。

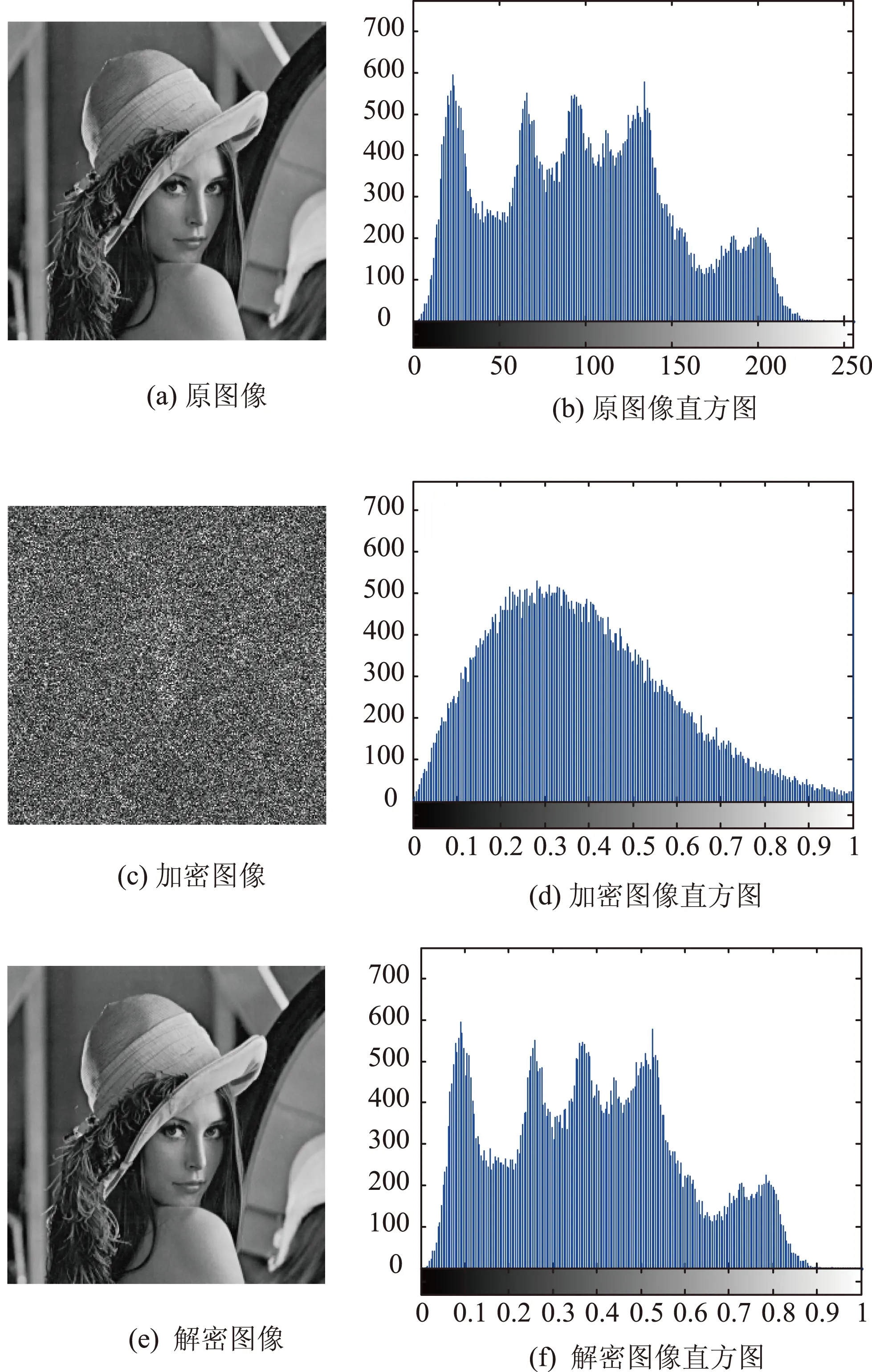
图2　加密解密图像和对应的直方图

本文方法将MPFRFT周期数、阶数和向量参数等组成的密钥进行结合，不需要传输随机相位矩阵，同时保持较高的安全特性。但是加密算法的抗攻击性是图像加密必须考虑的问题。加密算法的抗攻击性可以利用解密图像与原图像的平方根误差(MSE)进行描述，MSE的计算公式如下[11]：

(10)

其中E表示加密图像，X表示原图像，n, m表示像素位置。

图3给出了本文提出算法、MPFRFT双随机相位编码(double random phase, DRP)算法、FRFT双随机相位编码算法等对图像进行加密和解密方法得到的MSE。从图中可以看到本文提出的方法与MPFRFT双随机相位(加密方法的MSE非常接近，但是本文所提方法的密钥要比MPFRFT随机双相位加密方法的密钥少若干个数量级，其中具体量级与加密图像的维度有关。如果图像是M×N维度，则密钥空间将减少O(1/max(m,n))。而对于FRFT双随机相位编码加密方法在MSE上稍小于其他两种方法，而且其密钥数量与MPFRFT双随机相位加密方法具有相同数量级。所以本文所提加密方法相较于MPFRFT双随机相位编码和FRFT双随机相位编码方法具有很小的密钥空间，但是仍然保留较强的安全性和抗攻击能力。

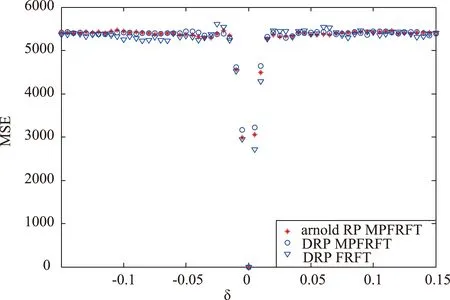
图3　不同加密方法对应的MSE

4　结　语

本文所提算法是在MPFRFT和ARNOLD算法基础上，利用ARNOLD变换对相位矩阵进行置乱，再利用MPFRFT进行图像加密。相对于传统的MPFRFT双随机相位加密方法不需要传输随机相位矩阵作为密钥，减小了密钥空间，同时又具有很强的抗攻击性。下一步将结合国际最新的图像加密算法[12-13]，进一步设计更为有效的加密结构和方法，并用于海洋遥感图像加密传输等[14]领域中。

[1]Jun L. A no-key-exchange secure image sharing scheme based on Shamir’s three-pass cryptography protocol and the multiple-parameter fractional Fourier transform[J]. Optcis Express. 2012, 20(3): 2386-2398.

[2]ZHU B, LIU S, and RAN Q. Optical image encryption based on multifractional Fourier transform [J]. Opt letter. 2000, 25(16): 1159-1161.

[3]Pei S C, Hsue w L. The multiple-parameter discrete fractional Fourier transform [J]. IEEE Signal Processing Lett. 2006, 13(6): 329-332.

[4]张楠, 夏玮, 赵子平. 基于混沌系统的彩色图像小波域加密算法[J]. 天津师范大学学报: 自然科学版, 2013, 33(2): 43-47.

ZHANG Nan, XIA Wei, ZHAO Zi-ping. A wavelet domain encryption algorithm for color image based on chaotic system [J]. Journal of Tianjin Normal University: Natural Science Edition. 2013, 33(2): 43-47.

[5]孙晓兵, 保铮. 分数阶Fourier变换及其应用[J]. 电子学报. 1996, 24(12): 60-65.

SUN X, BAO Zheng. Fractional Fourier Transform and Its Applications [J]. Acta Electronica Sinica. 1996, 24(12): 60-65.

[6]陶然, 邓兵, 王越. 分数傅里叶变换及其应用[M]. 北京: 清华大学出版社, 2009.

[7]Shih C C. Fractionalization of Fourier Transform [J]. Opt Comm. 1995, 48: 495-498.

[8]LANG Jun, TAO Ran, WANG Yue. The discrete multiple-parameter fractional Fourier transform [J]. Science China Information Sciences, 2010, 53(11): 2287-2299.

[9]李洋, 张靖, 石教华, 张晓丽. 目标航迹融合质量度量方法研究[J]. 电子科学研究院学报, 2015, 10(3): 94-100.

[10]QI Dongxu, ZOU Jiancheng, HA Xiaoyou. A new class of scrambling transformation and its application in the image information covering [J]. Science in China (Series E). 2000, 43(3): 304- 312.

[11]向涛, 余晨韵, 屈晋宇, 罗小松. 基于改进AES加密算法的DICOM医学图像安全性研究[J]. 电子学报. 2012, 40(2): 407-411.

[12]Jun L, Jing Z. Optical image cryptosystem using chaotic phase-amplitude masks encoding and least-data-driven decryption by compressive sensing [J]. Optics Communications. 2015, 338: 45-53.

[13]李雪梅, 陈亚云, 王若鑫. 基于FPGA的密码算法测试平台设计与实现[J]. 北京电子科技学院学报,2014, 22(2): 70-73.

[14]Yang Li, Kuisheng Liu, Ran Tao, and Xia Bai. Adaptive Viterbi-Based Range-Instantaneous Doppler Algorithm for ISAR Imaging of Ship Target at Sea. IEEE Journal of Oceanic engineering. 2015, 40(2): 417-425.

李洋(1983—)，男，辽宁省锦州市人，博士，工程师，主要研究方向为图像加密、多目标跟踪、信息融合等方面的研究工作；

E-mail：seenightrain@qq.com

王兆伟(1982—)，男，天津市人，博士，工程师，主要研究方向为通信网络设计；

徐山峰(1981—)，男，河北省人，硕士，高级工程师，主要研究方向为大型信息系统的总体设计；

张永利(1971—)，女，黑龙江省人，博士，高级工程师，主要研究方向为信号处理研究。

Image Encryption Algorithm Based on Multiple-parameter Fractional Fourier and Arnold Transforms

LI Yang, WANG Zhao-wei, XU Shan-feng, ZHANG Yong-li

(China Academy of Electronics and Information Technology, Beijing 100041, China)

The image encryption by multiple-parameter fractional Fourier transform (MPFRFT) and double random phase encoding can provide the wider key space, and the encrypted image has the better security. However, random phase matrix, as keys for decrypting the data will be transferred with the encrypted image, which is not safe and discommodious. In this paper, we propose a new approach for image encryption based on the MPFRFT and ARNOLD transform. In the proposed image encryption scheme, a phase matrix is scrambled as random phase matrix by ARNOLD transform, and then encrypting the phase encoded image with MPFRFT. The simulations shows that the approach still has the better security and resistance to various attacks.

Multiple-parameter fractional Fourier transform (MPFRFT); Arnold transform; image encryption.

10.3969/j.issn.1673-5692.2016.02.008

2016-02-01

2016-03-05