复杂机械结构中高频动响应能量有限元方法研究

撰文/赖运业

■518053 深圳华侨城文化旅游科技股份有限公司 广东 深圳



复杂机械结构中高频动响应能量有限元方法研究

撰文/赖运业

■518053 深圳华侨城文化旅游科技股份有限公司 广东 深圳

汽车、飞机和船舶等是当前三种重要的交通运输工具，为了将其运输性能提升到一个更高的档次，就需要从其结构系统入手，并且，随着技术的进步，这些结构系统变得越来越复杂。所以，必须要从实际情况出发进行相应的研究与分析。关键词：复杂机械结构；高频动响应；有限元方法

近些年，随着动力性能与结构轻量化的提升，更加突出的显示出了复杂系统的中高频动响应情况，如果长期发展下去，对于设备的正常运行必然会带来很大的伤害，所以，文章通过下文利用高频动响应有限元法对复杂机械结构的有关方面进行了探究，从而为有关单位及工作人员在实际工作中提供一定的方法论支撑。

该方法的研究进展分析

随着能量有限元研究方法的不断进步，相继的也带动了其有关应用的研究发展。

a Vlahopoulos N 等于1988年把渔船与护卫舰的结构制作成板的组合，在这个组合体中充分的应用了能量有限元分析方法，将组合体的相应特性分布有效的获取了出来，在真实的结构上应用能量有限元分析方法这还是较早的实例之一。张卫国与2005年，在能量有限元分析理论和周期结构理论基础上，对双向加筋圆柱壳受流体荷载是的内场声压分布与结构响应的现象进行了研究，其所带来的益处是：在PS理论的基础上，用能量有限元中能量传递系数的一部分等效了加强筋的影响，并且，从辐射阻抗与附加质量的角度出发分析考虑了外部重流介质对结构的影响，同时，在航天器结构与船舶结构中都有效的证实了这种研究方法的可行性。此外，点焊处节点的能量转移系数的相关理论也被，Vlaho-poulos N 等推导研究了出来。

b为了对复合材料结构与厚板高频响应情况进行充分的分析与考虑，

Mindlin板的能量流方程被Park Y H 等推导了出来，其中，对转动惯量与剪切变形是如何影响高频响应的相关内容进行了分析与考虑。

Yan X在这方面的研究也做出了很多的贡献，他的研究主要是假设在均匀扩散场的基础上，对向异性板波动群速度的不均匀分布没有进行考虑，然后将面内波的能量有限元方程与负荷结构内弯曲波的方程推导了出来。在以上研究的基础上，Lee S M又将结构损耗因子与角平均化的群速度应用了进去，从而对非均匀扩散场内波群速度的角度依赖性情况进行了分析。此外，对层合材料间的剪切效应在谱单元法的基础上进行了分析。

c在设计优化研究层面，Dong J 等通过能量有限元研究方法对高频结构的优化设计问题与灵敏度问题进行了研究，Vlahopoulos与；Borlase通过能量有限元分析法优化了组尼分布的相关研究，并且，通过SEA结论和船舶简单结构进行了相应的论证。

上述的这些研究，在船艇、航空和汽车等实体结构中已经得到了初步的证实，然而，还是有很多方面需要进行扩展和强化，不能单单的只局限于耦合板结构中。应该向着更加复杂的领域内深入，还应该进一步复杂化载荷形式，转向稳态流场和周期点载荷中。

具体的研究情况分析

为了在复杂结构系统与复杂载荷环境中充分的应用能量有限元法，文章通过下文进行了着重的探究：

针对在复杂荷载条件条件一些大型复杂结构系统预示要求，对该研究方法进行探究，对比分析了梁、板、杆结构的能量有限元方程，具体表现为：

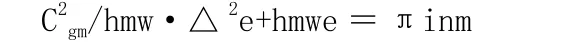
在此式子中，m构件一定波形的阻尼损耗因子用hm表示。m构件波形空间与时间输入功率用πinm表示，m构件一定波形群运行速度用Cgm表示。

对有限长圆柱壳体中振动能量分布情况在此基础上进行求解，如下图所示，横向周期载荷激励情况下，圆柱壳结构在轴向坐标0.5米处，随着轴向空间的不断变化，每个点的能量密度也会随之发生变化。并且比较分析了SEA法，二者有着各不相同的平均能量密度，分别为：3.19j/ m2和3.18j/m2，可见有有着非常小的相对误差，进而对圆柱壳弯曲振动的能量有限元分析方法的精确性。然而，能够得出，在轴线方向上，SEA的能量密度为一条直线。单纯的用一个平均值就可以表示出整个圆柱壳的能量密度，并且，随着不断远离了载荷点后，能量有限元也会不断降低，从而将能量密度在空间内的变化有效的进行了印证。从而得出能量有限元法精度较SEA法更高。

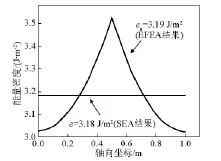
图1　

为了将某个截锥壳结构的高频动响应更加精确的预示出来，可以选择应用平板壳进行研究，取代了传统的曲面壳元法。这样能够大大的减少操作步骤。以某个单元为研究对象，假设面内位移与横向弯曲位不耦合，从而对各自的变形特征分别进行研究后再进行整合。在组装单元时，因为并非会在相邻的平面内存在相邻平板壳元，所以，对弯曲波应该同时进行考虑，例如剪切波与纵向波之间的耦合，所以，在节点的能量传递矩阵中将复杂多波形构建了起来。将能量有限元方程在此结果的基础上可以组建起来，此外，再同相关理论结合起来，将复杂结构的高频声振耦合相应方程也能够得出来，在此环节中，不但对声场和弯曲波的耦合进行了考虑，同时，对结构系统中多波间的功率传递也进行了考虑，这样同具体情况就会更加接近。在此前提下，对面源荷载、随机激励载荷、湍流场、脉动载荷与点源载荷的有关情况都进行了分析。

同时，因为瞬态解在具体结构的高频响应中也具有一定的研究价值，但是，当前的一些有限元研究方法只对稳态解问题进行了考虑，这样，在时间边界条件的基础上，将结构高频瞬态能领密度方程得了出来，这样为空间分布结构、瞬态时间和频率响应的研究奠定了基础。

在该研究的及基础上，将预示软件在能量有限元研究方法的基础上制定了出来，此软件在获取单元节点信息时，应用了当前商业软件中的一些有限元网格。之后通过能量有限元将结构耦合和刚度矩阵推导了出来。

结语

通过上文的分析能够得知，能量有限元法能够证明高频响应在复杂机械结构中不但将组尼、载荷、结构空间细节的分均匀分布特征有效的体现出来。并且，其计算精度较高，计算量小。同SEA与FEM的优点充分的结合到了一起，在相对较短的时间内，该理论开始向着更深的层次的发展。并且，其应用领域也越来越广泛，特别是在目前新兴行业大型游乐设施机械与3D电影结合起来的飞行影院领域，有着很好的辅助设计作用，可见这项研究成果，对于我国生产加工行业的发展必将带来很大的帮助，因此，我们必须要高度的予以重视。

参考：

［1］妙霞，陈花玲，吴九汇.能量有限元方法基本理论及其研究.新方向［J］.应用力学报，2007，24（01）：61-66.

［2］解妙霞.能量有限元方法在飞行器仪器舱高频声振耦合问题中的应用研究［D］.西安：西安交通大学，2011.

［3］解妙霞，陈花玲，吴九汇.圆柱壳高频弯曲振动的能量有限元分析［J］.西安交通大学学报：自然版，2008，42（9）：1113-1116.

［4］陈花玲，解妙霞.能量有限元方法计算截锥壳体高频声振耦合软件v 1.0［P］.0176506，2009.

［5］游进，孟光，李鸿光.声振系统中高频能量流分析法研究进展［J］.振动与冲击，2012 31（11）：62-69.