鲁棒主元分析和稀疏表示方法在模拟电路错误检测中的应用

吴益锋,朱恒亮,曾　璇

(复旦大学 专用集成电路与系统国家重点实验室,上海 201203)



鲁棒主元分析和稀疏表示方法在模拟电路错误检测中的应用

吴益锋,朱恒亮,曾璇

(复旦大学 专用集成电路与系统国家重点实验室,上海 201203)

模拟电路错误检测问题,即重点是检测出模拟电路芯片存在错误后确定错误元件或参数的问题,对于进一步明确错误产生原因,在设计或制造中加以改进,有重要的意义.经典做法是通过预先设置错误,并仿真得到其对应的响应数据,构造“错误字典”,然后将测试信号与错误字典进行比对,识别其属于哪一类错误类型.本文提出一种基于数据稀疏表示方法来进行错误类型识别的新方法,它计算属于不同错误类型的数据在所有类型的数据构成的空间中的展开向量,根据得到的稀疏向量来判断其所属错误类型.对于稀疏表示方法无法进行准确分类识别的情况,采用SVM作为二级分类器进行修正.存在某些错误类型,其响应数据构成的空间之间线性相关性较强,对于稀疏表示后属于其中之一类型的数据,采用传统的SVM方法来加以辅助分类.在两个实验例子中,与SVM,Ada Boost以及没有加SVM辅助分类的单纯稀疏表示方法相比较,本文方法有更高的错误类型识别正确率.

错误检测； 支持向量机； 鲁棒主元分析； 稀疏表示

模拟电路和混合信号电路中的错误检测以及错误定位问题,是电路设计验证和电路原型特征描述的重要课题[1-4].模拟电路错误检测,也即错误元器件位置的确定[5],一直是一个比较困难的问题.一部分原因是模拟电路错误检测缺乏良好的错误定义模型以及在不断开电路连接的情况下测量节点电流的困难性；另外,电路具有非线性特性等因素也造成了一定的困难性.

模拟电路的错误一般指任何电路元件对于其名义取值的偏离,从而可能破坏电路性能的情况.这些错误可能是“硬错误”,即电路发生短路或开路；也可能是“软错误”,即电路元件参数值偏离了设计的名义值,但还没有超出可接受的极限.这些软错误可能来源于制造过程的工艺偏差、器件的老化或者一些寄生效应.很多错误检测技术着眼于某一元件发生错误的情况的“单错误”问题,但从现在设计的复杂性以及电路检测技术的实用性考虑,“多错误”模型是我们的研究重点和方向.在本文后面的理论以及测试电路例子中,我们都会考虑电路中的多个参数同时发生错误的情况,一方面这相比“单错误”问题更加接近应用问题的实际情况[6],另一方面,“多错误”情况增加了问题的复杂度,从而可以更好地说明本文所提出的方法在处理复杂问题时的优势.

1　相关工作

过去对模拟电路错误检测的方法研究基本上可以分为两类: 测试前仿真(Simulation Before Test, SBT)方法和测试后仿真(Simulation After Test, SAT)方法.SAT方法是先得到待测试电路的响应,然后计算电路参数,从而完成错误检测.SBT方法的要点是将电路的响应与“错误字典”(fault dictionaries)中各个错误分类的对应电路响应进行比较,判断其是否属于某一特定错误分类.由于SBT方法是基于已经生成好的电路错误字典,所以比SAT方法时间开销更小,故本文所述也是基于SBT方法.

在过去的一段时间里,模拟电路错误检测方面的研究无论是在系统级、电路板级还是芯片级,都取得了很多进展[7-10].在SBT方法的整个错误检测流程中,最关键的地方是错误分类的学习过程,也即错误字典的构造过程.

文献[3-4]提出使用神经网络来作为分类学习器,直接将对电路测试得到的响应数据输入到学习网络中,在这种不加任何数据前处理的情况下,即便是小规模的电路也会需要比较复杂的学习网络[3],模型的学习时间过长.文献[11-12]提出用小波变换对一开始得到的电路响应数据进行前处理后,再作为神经网络的输入,不过虽然小波变换通常来说是不错的数据处理工具,在实际的电路检测实时应用场景下,小波变换的基、阶数以及变换后小波系数的选择都具有主观任意性,不能很好地把握.

文献[10,13-14]等提出用支持向量机(Support Vector Machine, SVM)来对错误进行分类学习,主要使用了经典的SVM方法以及一些改进算法,如LS-SVM等.SVM的基本思想是: 通过某种非线性映射,将输入数据向量映射到一个高维的空间Z,在这个高维的空间Z中,构造最优分离超平面,使得在原空间不可分的数据在变换后的空间中变得容易分类.通过修改不同的核函数(变换后空间的内积函数),可以得到不同的分离曲面.在数据量很大的时候,SVM的学习是比较耗时的,对此,文献[15]提出了一些近似算法.近似算法可以减少计算时间,但是会使属于各错误类型的样例个数变差.文献[16-18]进一步阐述了这个问题,提出了bagging, boosting以及Ada Boost等方法.但是,仍然存在boosting这一类方法自身难以很好地在分类精度和分类多样性之间进行平衡的问题[19].

本文中我们采用鲁棒主元分析(Robust Principal Component Analysis, RPCA)与稀疏表示方法(Sparse Representation, SR)相结合来作为分类器.属于不同错误分类的数据具有不同的主元特征,通过鲁棒主元分析并计算其稀疏表示后,得到的测试数据在包含各个分类的总的空间上的展开.若一个测试数据只属于某一分类,则得到的表示向量是稀疏的,与其所属分类相对应的位置上的元素占主要部分.稀疏表示方法的主要问题是对于线性相关度大的数据无法准确分类,因此采取SVM方法进一步分类以提高分类精度.实验结果表明,特别是在有若干错误类型线性相关度很大的情况下,这种稀疏表示再加上SVM的方法,相比SVM、Ada Boost等传统方法,具有更好的分类正确率.

2　基于RPCA和稀疏表示的错误检测方法

本文基于RPCA和数据稀疏表示方法来构造基本的分类器,假设训练数据为D,测试数据为T,首先运用RPCA提取训练数据的主元特征,若Ui是D中第i类错误类型数据的特征基矩阵,则有

(1)

(2)

那么如果将一个测试数据在包含所有分类的训练数据形成的主元空间上展开:

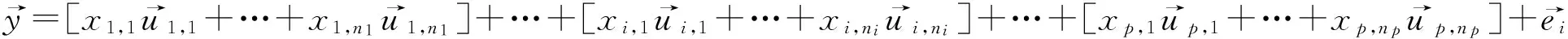
(3)

2.1鲁棒主元分析方法

RPCA方法可以有效地将原始数据的主元提取出来[20-21],假设有:

D=V+E,

(4)

D是数据矩阵,V是一个低秩的待恢复矩阵(即为RPCA后得到的矩阵),E是一个稀疏的噪声矩阵,传统的PCA方法根据E的2-范数最小的原则来计算V,但是这时即便E中只有一小部分的元被噪声污染或者是异常值,V就很有可能无法有效恢复.应用表明,RPCA采用0-norm具有更大优势,即:

min(rank(V)+‖E‖0),

(5)

‖•‖0代表求解一个向量的0-范数.但是这并不是一个容易求解的凸优化问题,文献[20]证明了在绝大多数情况下,将V的秩换为核范数(矩阵奇异值之和),将E的0-范数换为1-范数,在大概率下求出的解可以命中真实解,即最小化目标变为:

min(nuclearnorm(V)+‖E‖1).

(6)

这时我们就得到一个可以在多项式时间复杂度内求解的凸优化问题:

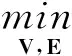
(7)

其中β是一个参数,‖•‖*表示核范数.对V进行奇异值分解(SingularValueDecomposition,SVD)后,可以分解为V=UΣV′,U和V′分别包含了V的行列主元,Σ是一个对角阵,对角线上是V的奇异值从大到小的排列.我们设定一个阈值,只选取那些能量占比比较大的奇异值.这样,就可以由训练数据D得到一个包含不同错误类型的特征基矩阵U.

2.2数据的稀疏表示分类

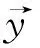
U=[U1,U2,…,Up],p为错误分类类型总数目,

(8)

(9)

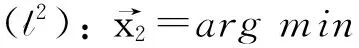
(10)

(11)[22]

(12)

该问题可以在多项式时间复杂度求解.

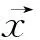
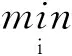
(13)

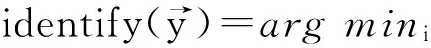
(14)

2.3SVM二级分类

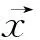
2.4步骤归纳

基于稀疏表示方法+SVM的模拟电路错误检测流程主要包括4个步骤: (1) 对电路进行仿真,提取响应数据D和T；(2) 用稀疏表示方法对D训练分类器M1,并得到“线性相关类型组”；(3) 用D中属于“线性相关类型组”的那些数据来训练SVM分类器M2；用M1对测试数据T分类,得其分类后所属类型；(4) 用稀疏表示方法对T分类,如果某测试数据的稀疏表示结果显示其属于某一“线性相关类型组”,则再用SVM方法进行分类.

3　实验和结果分析

本文用两个例子来对所提错误检测方法进行有效性的验证: 一个二级运放(two-stage opam)和一个电平转换电路(level shifter).两个电路所采用工艺分别为TSMC 180nm和SMIC 40nm, 电路仿真软件为HSPICE.

3.1电路例子以及错误类型设置

图1是二级运放,我们这里主要关注MOS管因制造工艺偏差造成的长宽误差.对现在的模拟电路单元来说[23],晶体管的宽比长大得多,所以电路的性能对于管长更加敏感.假设lmid,ldn,lup是3个参数,电路设计过程中,各个管子的沟道长满足L(M4)=L(M5)=lmid,L(M1)=L(M7)=ldn,L(M0)=L(M2)=L(M3)=lup.当这三个参数实际取值偏离设计值20%,就视为发生错误；同时考虑到工艺偏差,错误参数之外的其他参数在其各自设计值的5%以内随机偏离.所提取的二级运放的响应数据向量包含增益、单位增益带宽、相位裕度、跨导等,这些指标也是这个电路的性能优化目标.其错误类型设置如表1所示.

注: ↑和↓分别表示实际值比名义值偏大或偏小.

具体来说,例子中的运放设计规范(spec)是: Gain>80,Ugf > 1×107,Pm>-110,在设计的各个错误类型下,电路仿真得到的主要参数结果(每一错误类型的结果取的是50次仿真结果的平均值)如下表2所示,仿真结果中带有灰度的数据表示不符合spec的结果,视为存在错误.相应地,图2是电平转换电路的电路图,表3中是其错误类型设置情况,这里我们主要关注的是模拟电路中某处导线电阻异常增大甚至发生开路的错误情况.R1,R2和R3是虚拟设置的导线电阻,开路时的电阻值设定为100MΩ,当非出错时,其阻值在数欧到数十欧之间随机分布.错误分类提取的响应数据向量包含电路输入点、输出点的电压最值,以及电源点和接地点的电流最值等(都是在一个周期内).

表2　运放具体错误类型下电路主要参数

3.2结果分析

对于每一错误分类,仿真生成100个响应数据向量D和T各50个.4种不同方法在T上的属于各错误类型的样例个数如表4所示.

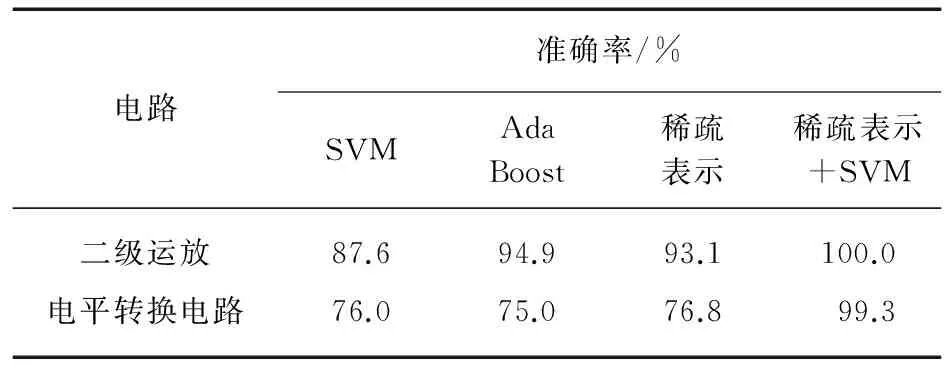
表4　4种方法属于各错误类型的样例个数比较

实验结果显示,我们提出的基于稀疏表示并使用SVM进行二次分类的方法在分类正确率上优于单使用稀疏表示、SVM或Ada Boost方法,在某些分类线性相关性强时,基于稀疏表示+SVM的方法具有更好的有效性和鲁棒性.

对于空间线性相关性较大的错误分类之间,采用SVM方法来二次分类.表5和表6分别是二级运放电路数据D在稀疏表示方法下、T在稀疏表示方法下、T在稀疏表示+SVM下的属于各错误类型的样例个数.格中数字表示原属于纵向分类类型的数据被最终分类为横向分类类型的数目,例如表5中第5列数据表示,属于第4类错误类型的50个测试数据,有35个分类正确,而15个被错误地分类为第6类错误.因为稀疏表示分类方法基于向量在空间中的线性展开,主要假设是: 相同错误类型的特征空间线性相关,而不同错误类型的特征空间线性相关性很小,从而属于某一分类的数据在总的空间上的线性展开系数向量是稀疏的；那么对于D在稀疏表示方法下分类具体结果中分类错误的情况,可以看作是分类类型之间线性相关性大所造成的.

表5中属于各错误类型的样例个数显示: 第4和第6类类型线性相关度大,第5和第7类类型线性相关度大(分别构成“线性相关类型组”),这也得到表5中各错误类型的样例个数的验证.表6中则为T在稀疏表示+SVM方法下各错误类型的样例个数,与表5结果相对比可以发现,对于属于线性相关度大的分类类型的数据,SVM二次分类可以进行很好地区分,大大提高了分类正确率.

类似地,表7,表8的数据显示了电平转换电路在稀疏表示+SVM方法下有效提高分类正确率的结果,表8是对表7得出的“线性相关类型组”的交叉验证,而表8的各错误类型的样例个数再次说明了对线性相关度大的分类进行SVM二次分类可以提高分类正确率.表5和表7,或表5和表8的数据对比也说明了表4中4种方法总体判别正确率在两个例子上的差异的原因: 电平转换电路的不同分类中数据空间线性相关程度更大,从而在电平转换电路中,稀疏表示+SVM方法的正确率比单纯的稀疏表示分类方法高出12.5%,运放例子中则为6.7%.

表5　运放电路训练数据D和运放电路测试数据T在稀疏表示方法下各错误类型的样例个数

表6　运放测试数据T在稀疏表示+SVM下各错误类型的样例个数

表7　电平转换电路训练数据D在稀疏表示方法下各错误类型的样例个数

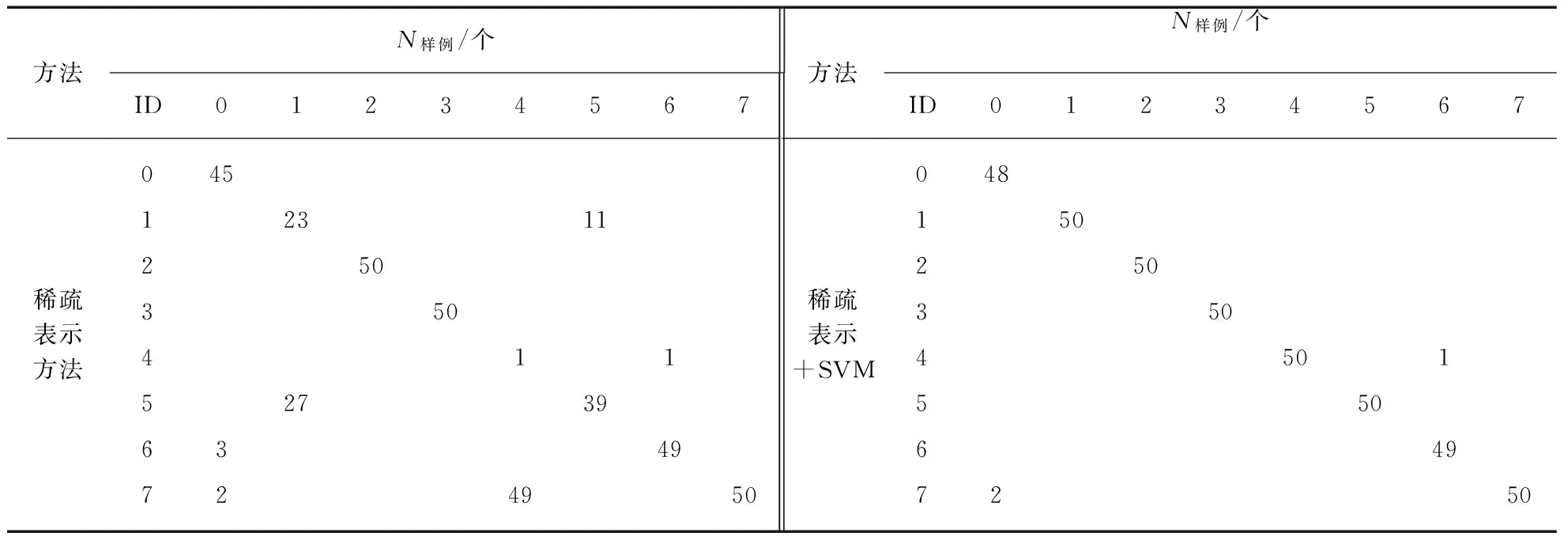
表8　电平转换电路测试数据T在稀疏表示方法、稀疏表示+SVM下各错误类型的样例个数

4　结　论

本文将鲁棒主元分析、数据稀疏表示方法应用于模拟电路错误检测问题,并与传统SVM方法相结合来提高分类判别的正确率.这种方法相比SVM、Ada Boost以及没有SVM辅助分类的RPCA方法,分类正确率更高,克服了其他几种方法面临的复杂性过大、分类效果不够好、性能表现不稳定等弊端.特别是当某些错误类型的数据空间线性相关性比较大时,本文方法可以更大地提高分类正确率,更好地显示出其鲁棒性.

[1]MAHDAVI S J S, MOHAMMADI K. Evolutionary derivation of optimal test sets for neural network based analog and mixed signal circuits fault diagnosis approach [J].MicroelectronicsReliability, 2009,49(2): 199-208.

[2]VOORAKARANAM R, AKBAY S S, BHATTACHARYA S,etal. Signature testing of analog and RF circuits: Algorithms and methodology [J].IEEETransactionsonCircuitsandSystemsI:RegularPapers, 2007,54(5): 1018-1031.

[3]AMINIAN M, AMINIAN F. A modular fault-diagnostic system for analog electronic circuits using neural networks with wavelet transform as a preprocessor [J].IEEETransactionsonInstrumentationandMeasurement, 2007,56(5): 1546-1554.

[4]YUAN L, HE Y, HUANG J,etal. A new neural-network-based fault diagnosis approach for analog circuits by using kurtosis and entropy as a preprocessor [J].IEEETransactionsonInstrumentationandMeasurement, 2010,59(3): 586-595.

[5]DEJKA W J. A review of measures of testability for analog systems[C]∥Imaginative Engineering thru Education and Experience: Proceedings of Southeastcon’77 Region 3 Conference. New York: Institute of Electrical and Electronics Engineers, 1977,1: 279-284.

[6]BANDLER J W, SALAMA A E. Fault diagnosis of analog circuits [J].ProceedingsoftheIEEE, 1985,73(8): 1279-1325.

[7]JANTOS P, GRZECHCA D, GOLONEK T,etal. Heuristic methods to test frequencies optimization for analogue circuit diagnosis [J].TechnicalSciences, 2008,56(1): 29-38.

[8]SUN Y C. Test and diagnosis of analogue, mixed-signal and RF integrated circuits: The system on chip approach [M]. London, UK: The Institution of Engineering and Technology, 2008.

[9]GISLASON P O, BENEDIKTSSON J A, SVEINSSON J R. Random forests for land cover classification [J].PatternRecognitionLetters, 2006,27(4): 294-300.

[10]CUI J, WANG Y. A novel approach of analog circuit fault diagnosis using support vector machines classifier [J].Measurement, 2011,44(1): 281-289.

[11]HE Y, TAN Y, SUN Y. Wavelet neural network approach for fault diagnosis of analogue circuits [J].IEEEProceedings-Circuits,DevicesandSystems, 2004,151(4): 379-384.

[12]AMINIAN F, AMINIAN M, COLLINS Jr H W. Analog fault diagnosis of actual circuits using neural networks [J].IEEETransactionsonInstrumentationandMeasurement, 2002,51(3): 544-550.

[13]TANG J Y, SHI Y B, ZHANG W. Analog circuit fault diagnosis based on support vector machine ensemble [J].ChineseJournalofScientificInstrument, 2008,6: 19.

[14]LONG B, TIAN S, MIAO Q,etal. Research on features for diagnostics of filtered analog circuits based on LS-SVM[C]∥AUTOTESTCON, 2011 IEEE.Baltimore, Maryland, USA: IEEE Press, 2011: 360-366.

[15]BURGES C J C. A tutorial on support vector machines for pattern recognition [J].DataMiningandKnowledgeDiscovery, 1998,2(2): 121-167.

[16]KIM H C, PANG S, JE H M,etal. Constructing support vector machine ensemble [J].PatternRecognition, 2003,36(12): 2757-2767.

[17]VALENTINI G, DIETTERICH T G. Bias-variance analysis of support vector machines for the development of SVM-based ensemble methods [J].TheJournalofMachineLearningResearch, 2004,5: 725-775.

[18]TANG J Y, SHI Y B, ZHOU L F,etal. Analog circuit fault diagnosis using Ada boost and SVM[C]∥International Conference on Communications, Circuits and Systems, 2008.Xiamen, China: IEEE Press, 2008: 1184-1187.

[19]WOLD S, ESBENSEN K, GELADI P. Principal component analysis [J].ChemometricsandIntelligentLaboratorySystems, 1987,2(1): 37-52.

[20]WRIGHT J, GANESH A, RAO S,etal. Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization[C]∥Advances in Neural Information Processing Systems.MA, USA: MIT Press, 2009: 2080-2088.

[21]WRIGHT J, YANG A Y, GANESH A,etal. Robust face recognition via sparse representation [J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2009,31(2): 210-227.

[22]DONOHO D L. For most large underdetermined systems of linear equations theminimal L1-norm solution is also the sparsest solution [J].CommunicationsonPureandAppliedMathematics, 2006,59(6): 797-829.

[23]BOOLCHANDANI D, GARG L, KHANDELWAL S,etal. Variability aware yield optimal sizing of analog circuits using SVM-genetic approach[C]∥SM2ACD, 2010. Gammarth, Tunisia: Springer, 2010: 1-6.

Analog Circuit Fault Diagnosis Based on Robust Principal Component Analysis and Sparse Signal Representation

WU Yifeng, ZHU Hengliang, ZENG Xuan

(State Key Laboratory of ASIC & Systems, Fudan University, Shanghai 201203, China)

Aiming at better solving the problem of fault diagnosis of analog circuits, a new method is proposed here, which is a combination of some different concepts and algorithms. It consists of robust principal component analysis, SVD, sparse representation and SVM. This method for fault analysis is especially useful and powerful when we cannot select out the most suitable features of circuit for diagnosis due to the lack of knowledge about the circuit itself, or just no enough training samples are got. In the test of the examples in our work, the new method has achieved better accuracy rate over SVM and Ada Boost framework based method.

fault diagnosis; support vector machine; robust principal component analysis; sparse signal representation

0427-7104(2016)01-0051-08

2015-02-12

国家自然科学基金(91330201)

吴益锋(1989—),男,硕士研究生；朱恒亮,男,讲师,通讯联系人,E-mail: hlzhu@fudan.edu.cn.

TN 47

A