线性规划在河道整治土方优化调度中的应用

缪海洋薛亚锋朱　林秦　伟（.江苏省太仓市水利局　太仓　5400　.淮河水利委员会　蚌埠　000 .江苏省太湖水利规划设计研究院有限公司　苏州　5000）

线性规划在河道整治土方优化调度中的应用

缪海洋1薛亚锋2朱林3秦伟1
（1.江苏省太仓市水利局太仓2154002.淮河水利委员会蚌埠233000 3.江苏省太湖水利规划设计研究院有限公司苏州215000）

农村河道一般淤积都较重，整治过程会产生大量土方，从节约投资角度考虑，土方的优化调度十分必要。本文以河段土方为变量，费用最小为目标函数，建立了线性规划模型，通过LINGO工具进行求解，结果表明该模型是可行的，对量广面大的农村河道疏浚整治具有重要意义。

线性规划河道整治土方优化Matlab解法LINGO工具

某地自2003年农村河道疏浚整治以来，平均每年疏浚河道土方有370多万m3之多。但用于囤浆的排泥场个数、位置、容量往往受客观条件限制，因此当工程量较大时，如何合理调度疏浚土方及优化排泥场布置，对工程投资会产生较大影响。本文建立的河道整治土方优化调度线性规划模型就是以各河段向对应排泥场输送的土方量为变量、以疏浚土方费用最小为目标函数，实现节省工程投资的目的，由于约束条件及目标函数均是线性的，方便利用各类线性规划工具进行求解。

1　模型建立

1.1排泥场

可能提供的排泥场位置有n个，每个排泥场最大可能囤浆量为Sj（j=1，…，n），假定排泥场填筑费用仅与疏浚总土方有关，排泥场设计总囤浆量即为疏浚总土方量。

1.2河段及疏浚土方单价

河段划分时根据实际需要，对较大河道可将一条河道划为几段，对较小河道可将邻近几条河道划为一段，原则上各河段土方差异不应过大。设共有m个河段，对任一河段i，其设计疏浚土方为Ai，其中运到第j个排泥场的土方量为xij，对应排距的土方单价为Cij，对于每一个河段在计算排距时可取其中心点。

1.3目标函数

以土方费用最小为目标，则建立目标函数为：

1.4约束条件

每个河段总土方平衡，即每个河段运到不同排泥场土方之和应等于该河段总土方：

每个排泥场最大容量限制，即不同河段运到某个排泥场的土方之和应不大于该排泥场最大容量：

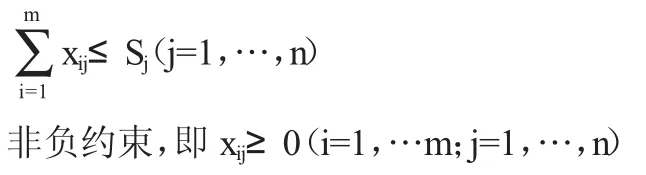
2　模型求解

该模型为典型的线性规划模型，在工程领域其求解比较常用的有Matlab及LINGO。Matlab解法又分为单纯形法、直接搜索法、遗传算法，但其在使用时一般工程人员难以掌握。LINGO主要用于求解线性规划、非线性规划等问题，功能十分强大，是目前最为流行的最优化软件之一。其特色在于内置建模语言，提供十几个内部函数，可以允许决策变量是整数，方便灵活，执行速度非常快，能方便与Excel、数据库等其他软件交换数据。在求解线性规划时，在LINGO窗口中输入的信息直观、便捷，初学者容易掌握。

3　应用实例

3.1项目概况

2014年实施的某中小河流治理重点县项目区共整治骨干河道39条，长约72.3km，土方57.6万m3。项目区为平原水网地区，可用于囤浆的废弃河塘及用于复垦的农田很少，因此如何处理大量泥浆是一大难题。目前的办法是围堰囤浆，待沉淀固结后集中外运。其中片区一共整治河道4条，总长13.7 km，总土方10.41万m3。片区一能提供的排泥场有3处，最大总容积约12万m3，河道及排泥场位置见图1。

3.2模型相关参数

以片区一为例，将该模型用于工程实践，相关参数如下：

3.2.1各排泥场最大可能囤浆量（m3）

3.2.2河段划分、设计土方量、排距及土方单价

1～3号河每条河道作为一个河段，4号河平均分为两个河段，5个河段设计土方（m3）：

各河段的排距取河段中心到对应排泥场中心的距离，统一选用Φ100mm泥浆泵进行水力冲挖，土方单价根据《江苏省水利工程预算定额》（2010年版）进行编制，则河段i的土方运到第j个排泥场的单价为Cij（元/m3）：

3.2.3目标函数

3.2.4约束条件

3.3模型求解

安装LINGO11.0，运行程序，即可得到如图2优化结果。

图1　片区一河道、排泥场平面位置图

图2　LINGO优化输出窗口图

3.4优化结果

土方费用：minf=1180804

各河段土方：x11=34900，x22=17700，x23=2500，x33=14200，x41=5100，x42=12300，x53=17400

排泥场容积：S1=40000，S2=30000，S3=34100

以上为以一个片区为例的优化结果，对整个项目区共安排16个集中囤浆点，每个排泥场的设计最大囤浆量为1万～5万m3。河道平均2km划分为一个河段，共划分成36个河段，原设计方案土方费用756.8万元，经过优化后土方费用约705.6万元，节省投资约6.8%。

4　结语

本文建立的模型与工程实践相结合，求解方法简单，容易掌握。尽管优化后单个项目区节省投资效率不算很高，但是如果项目区较大，细化河段划分，那么理论上节约投资效率还有进一步提升空间。

文中主要系数为土方单价，与排泥管线长度及选用机械形式有关，通过套用预算定额获得，工作量较大，不利于自动化计算，如何解决该问题有待进一步研究■

（专栏编辑：顾梅）