基于局部密度下降搜索的自适应聚类方法
2016-08-31徐正国姚佳奇
徐正国 郑 辉 贺 亮 姚佳奇
(盲信号处理国家科技重点实验室 成都 610041)
基于局部密度下降搜索的自适应聚类方法
徐正国郑辉贺亮姚佳奇
(盲信号处理国家科技重点实验室成都610041)
(xuzhg08@163.com)
聚类分析是数据挖掘中一个重要的研究领域,用于在无监督条件下,从混合类别的数据集中分离各样本的自然分组.根据不同的先验条件,现已提出了多种不同的聚类算法.但复杂数据集中存在的聚类个数未知、聚类形态混杂、样本分布不均匀以及类间样本数不均衡等问题,仍然是当前聚类分析研究中的重难点问题.针对这些问题,通过定义样本分布的局部密度,提出了一种利用类内密度有序性搜索聚类边界的新的聚类方法,能够实现在未知聚类个数条件下,对任意分布形态的数据样本集进行聚类.同时,通过自适应调节聚类参数来处理数据分布疏密度不一、类间样本数不均衡以及局部密度异常等特殊情况,避免样本类别被误划分和噪声数据干扰.实验结果表明,在6类典型测试集上,提出的新聚类算法均有较好的适用性,而在与典型聚类算法和最近发表的一种聚类算法的性能指标对比上,新算法也表现更优.
数据挖掘;聚类;局部密度;下降搜索;自适应
聚类分析是数据挖掘领域中一项经典的数据分析任务,也是无监督学习中日久弥新的一个研究课题.聚类分析的目标是要在无先验知识或有少量先验知识的条件下,将数据样本集划分成合理的组合,从而获得关于数据样本聚合形态的自然结构[1-2].
几十年来,国内外学者基于不同分析视角定义的自然分组,提出了不同类型的聚类算法[3-4].这些聚类算法被广泛应用于文本处理[5]、图像分析[6]、生物信息学[7]等诸多领域.随着聚类方法的研究越来越深入,已有的算法不断被改进,新的聚类思想陆续被提出,以适应更复杂的数据条件和更严苛的聚类需求,实现更理想的聚类划分.从KMeans、层次聚类、模糊聚类(fuzzingc-means,FCM)等经典算法[8-10],到后续提出的网格聚类[11]、DBSCAN(density-basedspatialclusteringofapplicationswithnoise)[12]、谱聚类(spectralclustering)[13]等算法,完成了从线性划分到非线性划分,从给定聚类个数到寻优搜索类别个数等不同数据条件和应用场景下的聚类分析任务.但时至今日,仍有2个问题没有得到很好地解决:
1) 感知不同的数据条件,实现自适应聚类,并能够同时处理任意分布形态的数据样本集,以及各类样本数不均衡和样本分布疏密度不一等情况.
2) 在聚类个数未知的情况下,使聚类结果接近最优的自然分组.
解决以上2个问题,能够使聚类分析的普适性和容噪性得到提升,实用范围得到扩展,因此也成为现今的研究热点.然而,近年国内外的许多研究工作大多针对上述的部分问题提出了改进方案,尚未有较为完整的解决方法[14-16].为此,本文提出了一种基于局部密度下降搜索的自适应聚类分析算法,能够实现在未知聚类个数的条件下,对任意分布形态的数据样本集进行聚类,同时能够根据数据分布疏密度自动调节聚类阈值,防止出现稀疏类别样本被当作噪声点的情形,还可根据预先设定的样本不均衡容忍度来实现不均衡类别的合理划分,避免小样本类别被误分的情况.
本文首先简要描述当前聚类分析研究的进展,指出其中存在的一些问题,为与本文的方法对比提供参考.然后阐述本文算法所涉及的聚类原理,并详细讨论算法中的一些关键步骤,给出实验结果,最后总结全文.
1 聚类分析研究进展
聚类算法根据对自然分组的不同定义,大体可被分为基于距离度量的方法、基于传播的方法和基于局部统计量的方法.
基于距离度量的聚类方法,其聚类目标是要使得类内的距离尽可能小,而类间的距离尽可能大.KMeans作为最早提出的聚类算法,只能对凸分布数据集做线性划分,并且类别样本数不均衡的情况会降低聚类准确性,这些问题为后续研究留下了许多改进的空间.以KernelKMeans[17]为代表的方法,通过引入核函数,将欧氏距离进行非线性映射,使之能够对非凸分布的数据聚类也具有较好的适应性.近年来,又提出了基于多核的聚类分析方法[18],使得对类别的划分性能比单核更优.同样利用距离来度量样本之间的相似性,层次聚类方法[19]通过自顶向下的分裂或自底向上的合并过程实现逐层聚合.谱聚类[20]利用样本之间的距离构造一个相似度矩阵,将样本聚类问题转换为子图划分问题,而聚类准则转换为使划分后的子图内部相似性尽量大,子图之间的相似性尽量小[13,21-22].谱聚类算法能够在任意分布的样本空间上聚类,且收敛于全局最优解.
尽管聚类算法在适用性上不断地被改进,但从先验条件上看,其中一些方法需要显式地指定聚类个数.目前,有文献[23-25]通过引入各种判据来识别最佳聚类数,通常的做法是遍历搜索可能的聚类数取值区间,观测以Gap统计量或特征值为依据设计的聚类指标的变化[14,16],发现指标突变点,从而判断其为最佳聚类数.但这种遍历搜索方法的弊端是搜索区间太大导致计算量过大,使得算法并不实用.
为了能够自适应地探测样本集中可能存在的最优聚类个数,基于传播和基于局部统计量的聚类方法从原理上改变了以距离度量定义“自然分组”的聚类准则.基于亲密度传播(affinitypropagation)的聚类方法[26-28],将样本之间的距离转换为吸引度.某个样本点对其他数据点的吸引力之和越大,越有可能成为聚类中心.而以DBSCAN为代表的基于密度的聚类方法,通过定义样本在局部邻域内的密度,将一个自然分组看作是由低密度点围绕高密度点形成的团簇.最近,Rodriguez等人[29]在《Science》期刊上提出的快速聚类算法,同样依据局部密度来确定聚类中心及其半径,但该算法在聚类过程中需要人工辅助决策.为了解决其中存在的问题,一年来又产生了相应的改进工作[30-31].与基于局部密度类似的还有基于网格的方法[32-33],把样本空间以网格切分,计算各网格中的局部统计参数(均值、方差、分布等),利用这些信息完成聚类.另外,Mean-Shift[34]综合了基于核和密度的方法,采用核密度估计算法搜索出密度最高的点作为聚类中心来实现聚类.虽然这类算法避免了要求指定聚类数,但在抗噪性能上,类间样本数不均衡、样本分布疏密度不一等情况并没有得到很好解决[31].
2 局部密度与聚类
在阐述本文算法之前,先给出局部密度的定义,并讨论其与聚类之间关系和性质,以便更好地说明本文算法的设计思路和实现原理.
定义1. 局部密度.对于任意数据样本i,其局部密度ρi由样本间距离di j和截断距离dc确定,即
其中,ψ(di j,dc)可以采用阶跃函数形式:
也可采用高斯核函数形式:
实验表明,2种局部密度的定义对计算结果影响不大,因此为了减少计算量,在后续的分析中都采用阶跃形式定义的局部密度.图1给出了4种不同数据集的样本局部密度分布情况.

Fig. 1 Local densities of sample data sets.图1 数据样本集局部密度图
事实上,不论采用何种算法,聚类结果应该符合人对自然分组的直观判断,即在几何形态上,特征空间中数据样本分布应该在某一观测尺度ε下具有显著的团簇聚合特性.同时,观察图1中各数据集的局部密度分布可以发现,一个团簇中的局部密度呈现了不同程度的高低有序分布.利用拓扑分析的方法,可以将这种直观特性作更为严谨的表述,也就是说,对于一个局部密度ρ均匀分布的理想聚类,在拓扑结构上应该具有ε-连通性和ρ-有序性.
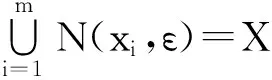
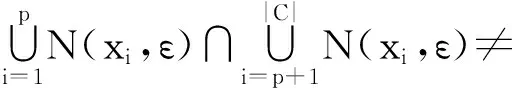
(4)
其中,|C|≤|X|,为样本集中集合的个数,则称集合X是ε-连通的.
由以上定义可知,ε-连通性是形成一个聚类的必要非充分条件,而为了说明聚类中的ρ-有序性,下面先给出聚类边界和理想聚类的定义,再对ρ-有序性进行证明.
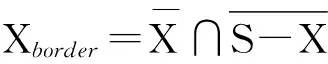
定义4. 理想聚类.样本集S中的理想聚类X为∀xi,xj∈X,N(xi,ε)∩Xborder=∅,N(xj,ε)∩Xborder=∅,满足|N(xi,ε)|=|N(xj,ε)|>1和ε-连通性的最大子集.
定理1. 对于由理想聚类混合而成的样本集,各理想聚类中样本点的局部密度从聚类内部向边缘呈现单调变化的趋势.
证明. 设样本集S中各聚类均为理想聚类,X⊂S,xb∈Xborder,令D=N(xb,ε)X,下面分2种情况讨论:
1) D=∅.
此时该边界区段不与其他聚类交界.对于从聚类内部到该边界区段的各样本点xi,其局部邻域所包含的样本点个数|N(xi,ε)|逐渐减少.
2) D≠∅.
此时理想聚类X与样本集S中另一理想聚类Y交界,则D⊂Y.设ρX,ρY分别表示X和Y内部的局部密度.
① 当ρX<ρY时,从聚类内部到该边界区段的各样本点xi,其局部邻域所包含的样本点个数|N(xi,ε)|单调递增;
② 当ρX>ρY时,从聚类内部到该边界区段的各样本点xi,其局部邻域所包含的样本点个数|N(xi,ε)|单调递减;
③ 当ρX=ρY时,从聚类内部到该边界区段的各样本点xi,其局部邻域所包含的样本点个数|N(xi,ε)|无变化,又由于D≠∅,即X′=X∪Y是ε-连通的.此时,X′是一个理想聚类,且|X′|>|X|,这与X是理想聚类的条件矛盾,因此,该情况不成立.
综上所述,根据局部密度定义有,理想聚类中样本点的局部密度从聚类内部向边缘总是呈现单调变化趋势.
证毕.
这里需要注意的一个特殊情形是呈线状分布的数据集,此时可认为聚类中的每个样本均处于聚类的边界,即ρborder=ρinner,如图1中pathbased数据集中环状区域所示.这将作为一种特殊情况在聚类算法中进行有针对性的处理.
而对于一般情形中的聚类Z,其样本的局部密度ρz可以由n个超球面的理想聚类的局部密度ρ(ri,ci),i∈[1,n]逼近,其中ri和ci分别为各超球面聚类半径和中心.同时考虑到噪声数据ξ的影响,于是ρz可表示为
(5)
因此,可认为是由密度散布均匀的理想聚类经噪声干扰、局部变形、类间混叠等因素变化而成.这也是在第3节设计基于局部密度下降搜索聚类算法时要重点解决的问题.
3 基于局部密度下降搜索的聚类算法
与以往基于局部密度的聚类算法不同的是,现有算法大多以寻找聚类中心和聚类半径为聚类目标,而本算法采用搜索聚类边界为聚类依据,一旦聚类边界圈定,聚类自然也就形成.
根据第2节中关于聚类连通性的定义和理想聚类中局部密度有序性的证明,本文提出了基于局部密度下降搜索的聚类算法(localdensitybasedclusteringbydescendingsearch,LDCDS).
首先给定一个较小的局部半径,按照式(1)计算各样本点的局部密度,然后以合适的搜索半径,从局部密度最高的样本沿着密度下降的方向进行搜索,并将沿途的样本点标注为与最高密度点相同的类别,当某方向再无邻域样本点,或邻域样本点的局部密度开始增大时,停止该方向的搜索,并确定聚类的边界.循环迭代以上步骤,完成对所有样本的类别标注,聚类结束.
当然,实际情况中数据样本的局部密度不会是理想的有序散布.为了处理聚类搜索过程中遇到的如类内样本点散布不均匀导致的局部密度峰谷、类间疏密度不一、类别混叠时的边界探测、线状分布与球状分布混合以及类别之间样本数不均衡等各种情况,搜索过程中还需有针对性的判决筛查.下面将就这些关键步骤一一说明.
1) 类内样本散布不均导致的局部密度极值.
由于样本点非均匀散布可能导致局部密度极值的出现,使得当密度下降搜索到此处时误将局部极小值点判为聚类边界.而实际中,若出现局部极值点,其邻域会成为类内的一个“孤岛”,在最后的聚类合并过程中,这些“孤岛”将划归周边的大类.合并“孤岛”的尺度由类别样本不均衡容忍系数α决定,即样本数少于某一比例的小类将并入其周边的大类.
2) 类间疏密度不一.
图1中jain数据集显示了2个类别疏密度不一的情况,DBSCAN这类基于密度的聚类算法,通过给定半径距离寻找聚类中心,对类内密度低于其他类别的样本子集,容易误判为噪声.而本算法采用搜索半径自适应的方式,从类内密度高的样本子集向类内密度低的样本子集不断扩大搜索半径,也就是不断在自适应不同类别的疏密度,降低分布稀疏的类别样本的误判概率.同时,为了防止搜索半径在迭代过程中被快速扩大,其被设计为
(6)
其中,r为初始搜索半径,n为迭代搜索的次数.
3) 类间样本混叠.
当2个聚类存在少量样本交叠时,采用密度下降的方式对类别边界进行搜索,密度下降的趋势可能会通过交叠连通的区域沿着另一个类别低密度的边缘传播出去,造成样本误分类的情况.一般来讲,当2类样本可分时,其类间交叠区域的分布形态要显著区别于各自类内的分布形态.这里采用对类别混叠区域进行分布形态判断的方法来识别当前搜索位置是否处于类间交叠区,由此来停止对该方向的搜索.
判断局部样本分布形态变化可以采用主成分分析的方法.主成分分析是一种用于提取数据分布特征的经典而有效的方法.通过矩阵特征值分解,得到数据散布的主成分方向及其正交投影空间.当搜索半径之内局部样本散布的主成分方向发生较大突变时,可认为此时聚类形态发生了改变,搜索可能处于类别边界或者类间混叠区.这里,我们采用主成分分析中最大特征值和次大特征值的比值,来衡量第i步搜索时样本点局部邻域分布形态的变化,令γ(i)=λ1λ2,当γ(i+1)>β γ(i)或γ(i+1)<γ(i)β时,判断为局部散布形态发生突变.
由于聚类是一个无监督的过程,对混叠区域的样本做类别划分,具有一定的主观因素,为了选取一个合理的判决阈值β,我们根据2个正态分布混叠变化过程的仿真实验,得到一个符合观测预期的经验值,在算法中该值一般取值为3.
综合以上3点,我们可以得到在局部密度下降搜索过程中,较为完整地解决任意分布形态聚类、类别样本数不均衡、类间疏密度不一致等情况的聚类算法.算法1给出了这些关键步骤的处理流程.
算法1. 局部邻域搜索与类别标注Labeling.
输入:中心点c、搜索半径R、前序搜索状态s(i-1);前序邻域分布形态γ(i-1);
输出:样本类别标签Labels.
① 判断前序搜索状态是否为初始状态0.若是,执行步骤②;若否,执行步骤⑥.
② 判断该中心点c是否被标记过.若是,则返回.
③ 依据搜索半径R,搜索给定中心点c的局部邻域样本点N(c,R).若N(c,R)=∅,执行步骤④;否则,执行步骤⑤.
④ 按式(6)扩大搜索半径R,并返回.
⑤ 找出N(c,R)中占比最多的类别.若多数样本未被标注,则为中心点c生成新的类别标签;否则,将c标注为与邻域主要类别相同的标签.继续执行步骤⑦.
⑥ 计算N(c,R)的分布形态γ(i).若γ(i)较前序形态γ(i-1)发生较大变化,则返回.
⑦ 搜索N(c,R)中密度小于ρ(c)的样本点集.若样本点集为空,则返回;若非空,则将集合中的所有样本标注为与c相同的类别,并将其中每个样本点赋为中心点c,重复步骤①.
值得指出的一点是,从定义1可以看出,样本局部密度的计算过程隐式地完成了将数据集从原始m维空间向1维空间的映射,在后续的聚类过程中,样本的类别标注只与其搜索半径内各样本点的局部密度有关,与原始数据的维数无关.因此本算法的适用范围不受限于数据集的维数,但为了更好地显示本算法的性能和结果,也便于读者理解,第4节均采用2维数据集进行实验验证和对比测试.
当然,高维和稀疏数据空间可能造成最近邻失效的情况[35],但该问题是采用距离来度量样本间相似性的聚类方法所面临的共同问题.因此,面对高维数据,需要先将其相似性度量进行有效处理[36],在此基础上使用本方法完成聚类.
4 实验结果
4.1LDCDS算法聚类测试结果
为了测试本文提出的LDCDS算法的聚类性能,我们选取了在聚类分析研究中广为采用的6类测试数据进行实验,测试数据集的基本信息如表1所示:
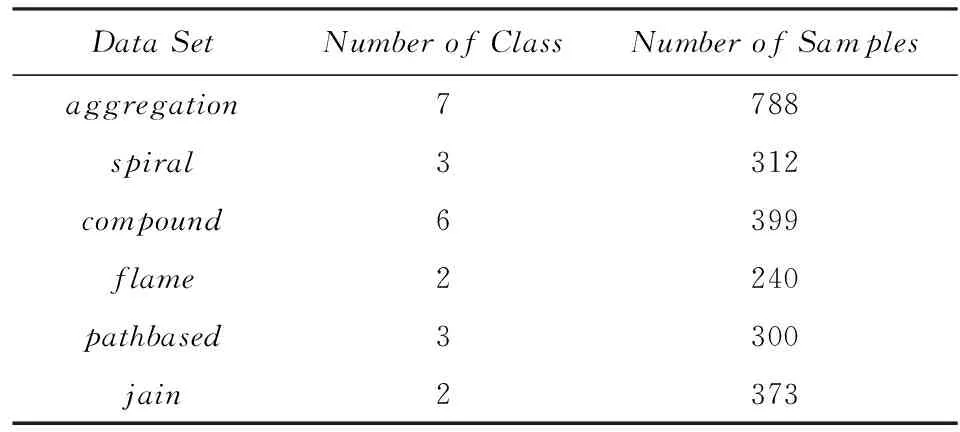
Table 1 Attributes of Experiment Data Sets表1 实验数据集基本属性
图2显示了采用LDCDS算法对表1中各数据集的聚类结果.作为对比,图3显示了一种新近提出的,同样基于局部密度的聚类算法[29]的测试结果.
从图2可以看出,LDCDS算法均能给出符合直观判断和真实聚类情况的结果,并能有效处理这6类测试数据集中包含的非凸分布、疏密度不一、类间混叠、类别样本数不均衡以及有噪声干扰等特殊情况.其中,有2个值得注意的地方是,在pathbased数据集中聚类结果将属于1个类的外环样本划分为2个类.原因是按照LDCDS算法对类别边界的搜索,在某一局部区域出现了大于搜索半径的间隙,使得该区域被误判为1个聚类的边界,同时由于该间隙处于环状分布的中部,使得被分为2个聚类的样本数相当,在最后的聚类合并阶段,也无法实现2个类别的融合.另外,对于compound数据集而言,测试样本集虽然被标注为6类,但在无类别标签的情况下,将图中右上区域稀疏分布的样本点视为密集分布的样本点的边界噪声,也符合直观判断,因此,从基于密度下降搜索的聚类准则和人对聚类的直观判断来讲,该聚类结果的准确性是可以接受的.而在文献[29]所提算法的测试结果中,则存在着一些明显的类别误判.
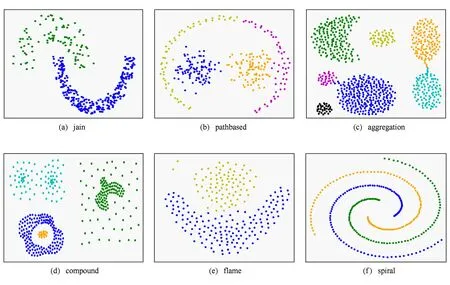
Fig. 2 Clustering results of LDCDS.图2 LDCDS聚类算法的测试结果
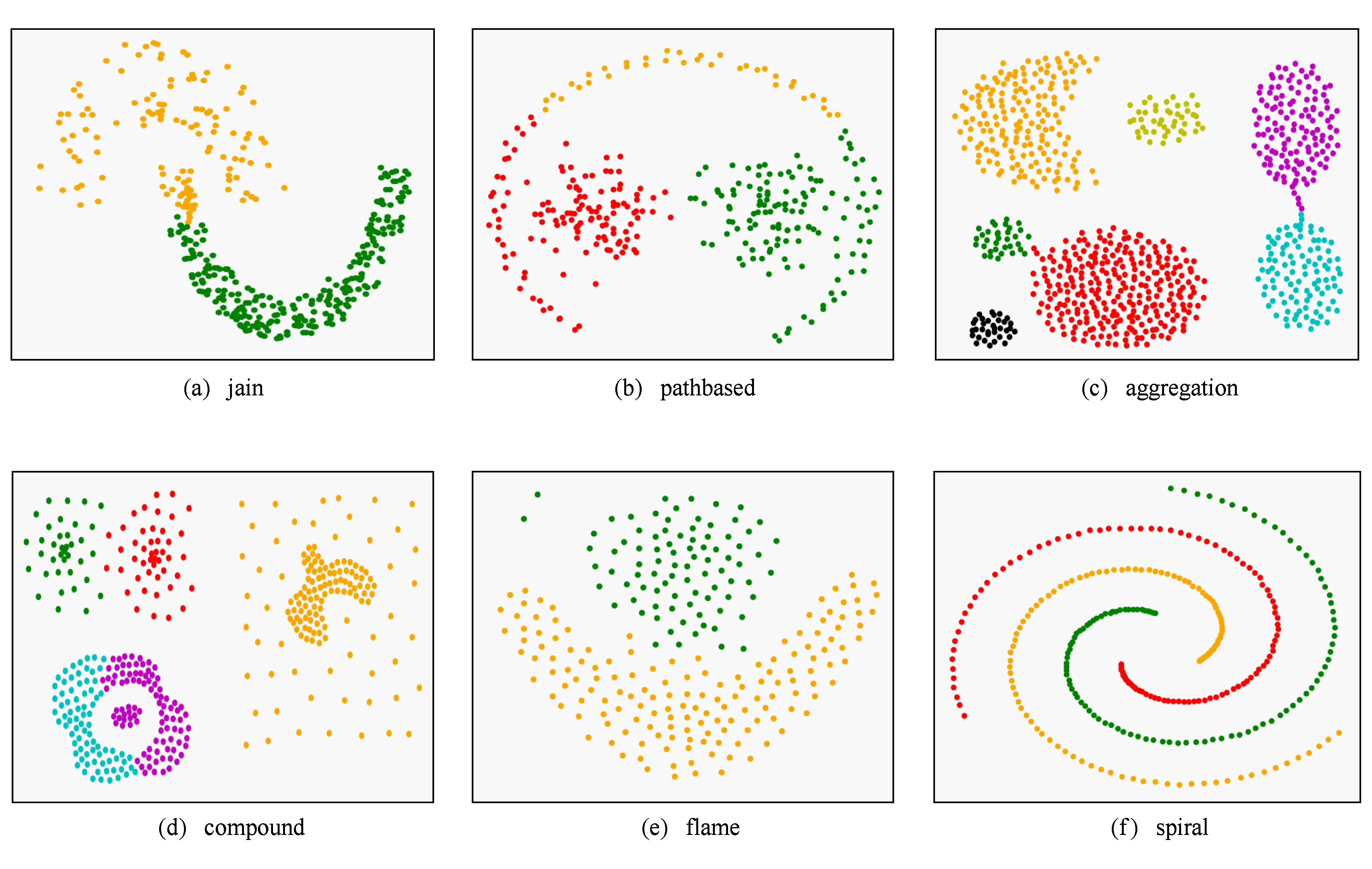
Fig. 3 Results of clustering by fast search and find of density peaks in ref
同时,我们还基于文献[29]中使用的实验数据集对算法性能进行了测试,结果如图4所示.由于该文献提出的快速聚类算法,有对噪声数据的判断,而本文算法在对局部分布密致的区域完成搜索后,同样达到了其论文中显示的聚类效果,如图4(a)所示.同时,如果数据集中含有大量被认为是噪声的未分类样本点的话,其聚类结果也不尽合理,因此,本文算法除了在设定局部密度阈值实现噪声数据发现之外,还能够对噪声数据实现合理地类别划分,如图4(b)所示.
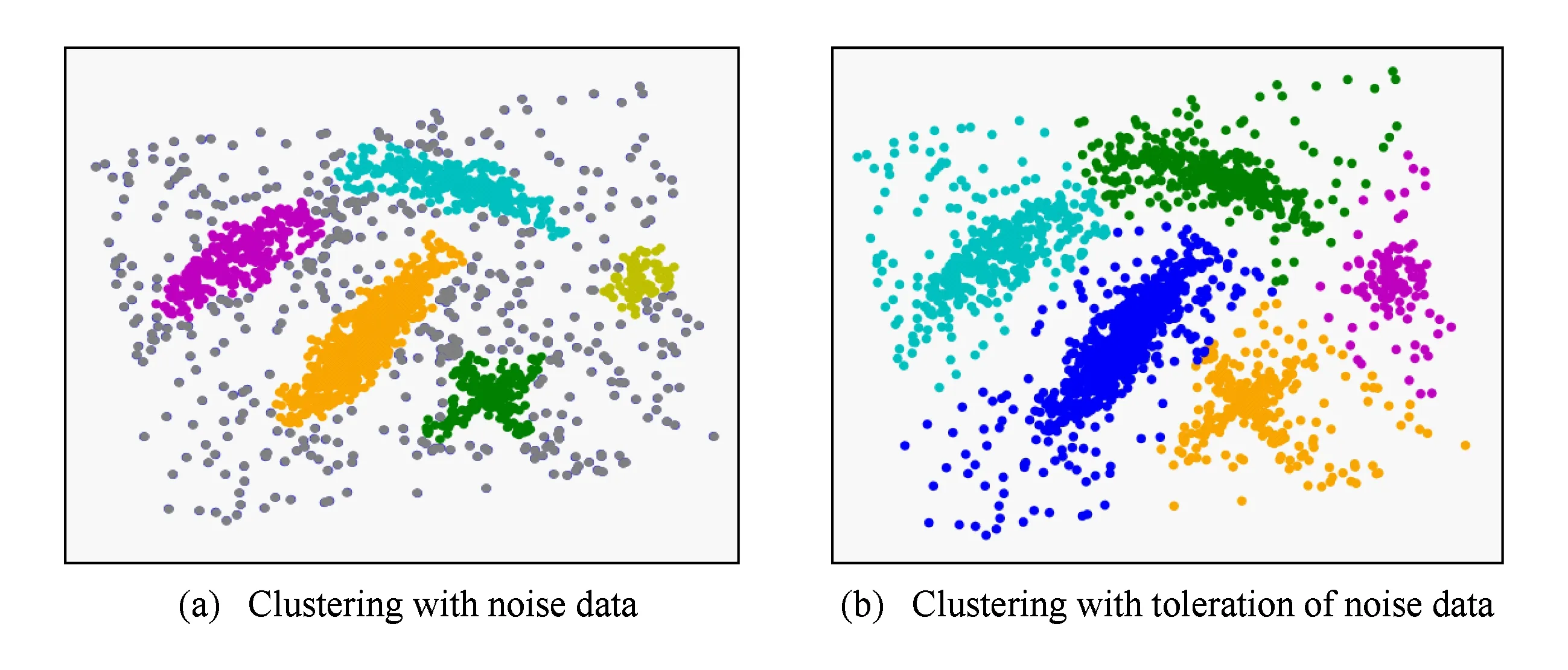
Fig. 4 Results of LDCDS with noise and toleration of noise.图4 LDCDS去噪和容噪聚类结果

Fig. 5 Performances of LDCDS comparing with typical and latest clustering methods.图5 LDCDS算法与典型的和最新的聚类算法的性能对比
4.2LDCDS算法与典型算法的性能对比
为了更加全面客观地比较本文提出的LDCDS算法与已有典型聚类算法的性能差异,我们选取了BatchKMeans,AffinityPropagation,MeanShift,SpetralClustering,AgglomerativeClustering,DBSCAN六类典型算法,其中BatchKMeans是KMeans算法的一个变种,通过批量式处理来减少聚类时间,而AgglomerativeClustering是层次聚类算法中采用合并方式进行聚类的一种.同时,我们也将文献[29]中提出的基于局部密度的聚类算法一同纳入比较范围.
这里采用2个不同的指标分别衡量各算法聚类结果的准确性.由于已知测试数据集中各样本的真实类别标签,我们选用校正Rand系数(adjustedrandindex,ARI)和校正互信息系数(adjustedmutualinformationscore,AMI)两个指标[37-38]来共同衡量聚类结果的性能.
ARI的取值范围是[-1,1],AMI的取值范围为[0,1],2个指标越接近1,表示聚类的结果与真实的类别分组越相近.各算法在图2所示的6类测试数据集上聚类的性能指标如图5所示.从图5中的2个指标的测试结果都可以看出,本文所提出的LDCDS算法的聚类性能多数情况都要优于其他算法,并且对于jain,aggregation,spiral三类数据集的聚类结果与真实情况基本吻合.综合2个聚类性能指标,本算法与文献[29]中所提出的算法性能相当,但对于不同类型的测试集,本算法的性能表现更为平稳.考虑到文献[29]的算法需要人工参与选定聚类中心,而本算法在参数设定的条件下,可完成自动聚类,无需人工干预,因此,本算法的适用性要更优于现有的一些聚类算法.
5 结 论
本文在总结现有聚类算法原理及其适用性的基础上,提出了一种新的基于局部密度下降搜索的聚类方法.相比于现有的各类典型聚类方法,本文所提出的算法,具有3个特点:
1) 不同于以往许多聚类算法寻找合适聚类中心的思想,本算法采用局部密度下降的方式来搜索聚类的边界,以此来完成对样本类别属性的标注过程.从数据样本空间的聚类拓扑结构来看,搜索聚类边界比确定聚类中心,具有更高准确性.
2) 能够在未知聚类个数的条件下完成自适应的聚类.并且,与之前采用搜索聚类数可能取值区间的方法不同,本算法在完成对所有样本的聚类标注之后,即可获得合理的聚类数,节省了在可能取值区间内反复搜索带来的计算开销和判别误差.
3) 能够同时处理含有类间数据分布疏密度不一、类间样本数不均衡和任意分布形态等情况的数据聚类问题.本算法采用了局部密度自适应因子,在搜索过程中通过调节搜索半径来感知数据分布密度的变化,并在类间样本不均衡容忍度参数的指导下,对少量局部密度异常区域进行重新类别归并,避免样本类别的误划分.
在算法性能的实验验证中,本文选取了6类常用的测试数据集,对本算法进行了测试,结果表明本文算法能够较好地对上述各种特殊的数据聚合情况进行处理.同时,本算法也与现有的典型聚类算法以及新近提出的一种聚类算法进行了聚类性能对比,综合2种聚类性能评价指标,本算法的聚类性能总体优于其他算法.但是,从算法的复杂性来讲,本算法由于存在迭代搜索的过程,其聚类过程的耗时要大于现有的一些算法,如何降低算法的复杂性是今后研究的重要工作.
[1]DudaRO,HartPE,StorkDG.PatternClassification[M]. 2nded.NewYork:JohnWiley&Sons, 2001
[2]JainAK.Dataclustering: 50yearsbeyondK-means[J].PatternRecognitionLetters, 2010, 31(8): 651-666
[3]GuanTao.Overviewofstatisticalclusteringmodels[J].ComputerScience, 2012, 39(7): 18-24 (inChinese)
(管涛. 统计聚类模型研究综述[J]. 计算机科学, 2012, 39(7): 18-24)
[4]JinJianguo.Reviewofclusteringmethod[J].ComputerScience, 2014, 41(11): 288-293 (inChinese)
(金建国. 聚类方法综述[J]. 计算机科学, 2014, 41(11): 288-293)
[5]BanerjeeS,RamanathanK,GuptaA.ClusteringshorttextsusingWikipedia[C] //Procofthe30thAnnualIntACMSIGIRConfonResearchandDevelopmentinInformationRetrieval.NewYork:ACM, 2007: 787-788
[6]HoreP,HallLO,GoldgofDB,etal.Ascalableframeworkforsegmentingmagneticresonanceimages[J].SignalProcessingSystems, 2009, 54(1//2//3): 183-203
[7]MadeiraSC,OliveiraAL.Biclusteringalgorithmsforbiologicaldataanalysis:Asurvey[J].IEEETransonComputatinalBiologyandBioinformatics, 2004, 1(1): 24-45
[8]BezdekJC,EhrlichR,FullW.FCM:Thefuzzyc-meansclusteringalgorithm[J].Computers&Geosciences, 1984, 10(2): 191-203
[9]FilipponeM,CamastraF,MasulliF,etal.Asurveyofkernelandspectralmethodsforclustering[J].PatternRecognition, 2008, 41(1): 176-190
[10]HuangChengquan,WangShitong,JiangYizhang.Anewfuzzyclusteringalgorithmwithentropyindexconstraint[J].JournalofComputerResearchandDevelopment, 2014, 51(9): 2117-2129 (inChinese)
(黄成泉,王士同, 蒋亦樟. 熵指数约束的模糊聚类新算法[J]. 计算机研究与发展, 2014, 51(9): 2117-2129)
[11]WangWei,YangJiong,MuntzR.STING:Astatisticalinformationgridapproachtospatialdatamining[C] //ProcofVLDB.SanFrancisco:MorganKaufmann, 1997: 186-195
[12]KhanK,RehmanSU,AzizK,etal.DBSCAN:past,presentandfuture[C] //Procofthe5thIntConfontheApplicationsofDigitalInformationandWebTechnologies.Piscataway,NJ:IEEE, 2014: 43-47
[13]ShiJ,MalikJ.Normalizedcutsandimagesegmentation[J].IEEETransonPatternAnalysisandMachineIntelligence, 2000, 22(8): 888-905
[14]WangJun,WangShitong,DengZhaohong.Surveyonchallengesinclusteringanalysisresearch[J].ControlandDecision, 2012, 27(3): 321-328 (inChinese)
(王骏, 王士同, 邓赵红. 聚类分析研究中的若干问题[J]. 控制与决策, 2012, 27(3): 321-328)
[15]CaiXiaoyan,DaiGuanzhong,YangLibin.Surveyonspectralclusteringalgorithms[J].ComputerScience, 2008, 35(7): 14-19 (inChinese)
(蔡晓妍, 戴冠中, 杨黎斌. 谱聚类算法综述[J]. 计算机科学, 2008, 35(7): 14-19)
[16]XiaoYu,YuJian.Gapstatisticandk-meansalgorithm[J].JournalofComputerResearchandDevelopment, 2007, 44(Suppl): 176-180 (inChinese)
(肖宇, 于剑.Gapstatistic与K-Means算法[J]. 计算机研究与发展, 2007, 44(增刊): 176-180)
[17]DhillonIS,GuanYuqiang,KulisB.Kernelk-means,spectralclusteringandnormalizedcuts[C] //Procofthe10thACMSIGKDDIntConfonKnowledgeDiscoveryandDataMining.NewYork:ACM, 2004: 551-556
[18]ZhaoB,KwokJT,ZhangCS.Multiplekernelclustering[C] //Procofthe9thSIAMIntConfonDataMining.Philadelphia:SIAM, 2009: 638-649
[19]GrabmeierJ,RudolphA.Techniquesofclusteringalgorithmsindatamining[J].DataMiningandKnowledgeDiscovery, 2002, 6(4): 303-360
[20]NgAY,JordanMI,WeissY.Onspectralclustering:Analysisandanalgorithm[J].AdvancedNeuralInformationProcessingSystems, 2001, 14: 849-856
[21]DingC,HeX,ZhaH.Spectalmin-maxcutforgraphpartitioninganddataclustering, 47848[R].Berkeley:NationalEnergyResearchScientificComputingDivision, 2001
[22]MeilaM,XuL.Multiwaycutsandspectralclustering, 442[R].Washington:UniversityofWashington, 2004
[23]TibshiraniR,WaltherG,HastieT.Estimatingthenumberofclustersinadatasetviathegapstatistic[J].RoyalStatisticalSociety, 2001, 63(2): 411-423
[24]MercerGM.Kernel-basedclusteringinfeaturespace[J].IEEETransonNeuralNetworks, 2002, 13(3): 780-784
[25]KongWanzeng,SunZhihai,YangCan.Automaticspectralclusteringbasedoneigengapandorthogonaleigenvector[J].ActaElectronicaSinica, 2010, 38(8): 1880-1886 (inChinese)
(孔万增, 孙志海, 杨灿. 基于本征间隙与正交特征向量的自动谱聚类[J]. 电子学报, 2010, 38(8): 1880-1886)
[26]FreyBJ,DueckD.Clusteringbypassingmessagesbetweendatapoints[J].Science, 2007, 315(5814): 972-976
[27]BruscoMJ,KohnHF.Commenton“clusteringbypassingmessagesbetweendatapoints”[J].Science, 2008, 319(5864): 726
[28]LuWeiming,DuChenyang,WeiBaogang,etal.Distributedaffinitypropagationclusteringbasedonmapreduce[J].JournalofComputerResearchandDevelopment, 2012, 49(8): 1762-1772 (inChinese)
(鲁伟明,杜晨阳,魏宝刚,等.基于MapReduce的分布式近邻传播聚类算法[J]. 计算机研究与发展, 2012, 49(8): 1762-1772)
[29]RodriguezA,LaioA,Clusteringbyfastsearchandfindofdensitypeaks[J].Science, 2014, 344(6191): 1492-1497
[30]ChenJinyin,HeHuihao.Researchondensity-basedclusteringalgorithmformixeddatawithdetermineclustercentersautomatically[J].ActaAutomaticaSinica, 2015, 41(10): 1798-1813 (inChinese)
(陈晋音, 何辉豪. 基于密度的聚类中心自动确定的混合属性数据聚类算法研究[J]. 自动化学报, 2015, 41(10): 1798-1813)
[31]ZhangWenkai,LiJing.Extendedfastsearchclusteringalgorithm:Widelydensityclusters,nodensitypeaks[EB//OL]. 2015[2015-05-21].http://arxiv.org//abs//1505.05610
[32]YangShanhong,LiangJinming,LiJingwen.Impactfactorofgriddensitybasedclusteringalgorithmformulti-density[J].ApplicationResearchofComputers, 2015, 32(3): 743-747 (inChinese)
(杨善红, 梁金明, 李静雯. 基于网格密度影响因子的多密度聚类算法[J]. 计算机应用研究, 2015, 32(3): 743-747)
[33]HuangHongwei,HuangTianmin.Extensionclusteringalgorithmbasedonrelativegriddensitydifference[J].ApplicationResearchofComputers, 2014, 31(6): 1702-1705 (inChinese)
(黄红伟, 黄天民. 基于网格相对密度差的扩展聚类算法[J]. 计算机应用研究, 2014, 31(6): 1702-1705)
[34]ComaniciuD,MeerP.Meanshift:Arobustapproachtowardfeaturespaceanalysis[J].IEEETransonPatternAnalysisandMachineIntelligence, 2002, 24(5): 603-619
[35]BeyerK,GoldsteinJ,RamakrishnanR,etal.WhenIs“NearestNeighbor”meaningful, 1377[R].Madison:UniversityofWisconsinMadison, 1998
[36]CaiTT,ShenXT.High-DimensionalDataAnalysis[M].Beijing:HigherEducationPress, 2010
[37]VinhNX,EppsJ,BaileyJ.Informationtheoreticmeasuresforclusteringscomparison:isacorrelationforchancenecessary[C] //Procofthe26thAnnualIntConfonMachineLearning.NewYork:ACM, 2009: 1073-1080
[38]VinhNX,EppsJ,BaileyJ.Informationtheoreticmeasuresforclusteringscomparison:variants,properties,normalizationandcorrectionforchance[J].JournalofMachineLearningResearch, 2010, 11: 2837-2854

XuZhengguo,bornin1985.PhDcandidateattheStateKeyLaboratoryofBlindSignalsProcessing,Chengdu.StudentmemberofChinaComputerFederation.Hismainresearchinterestsincludedatamining,machinelearning,networkanalysis,andbigdataprocessing.
ZhengHui,bornin1957.Seniorengineer.PhDsupervisor.Hismainresearchinterestsincludeblindsignalprocessingandintelligentinformationanalysis.

HeLiang,bornin1990.MastercandidateattheStateKeyLaboratoryofBlindSignalsProcessing,Chengdu.Hismainresearchinterestsincludeanomalydetectinandnetworkdetection.

YaoJiaqi,bornin1992.MastercandidateattheStateKeyLaboratoryofBlindSignalsProcessing,Chengdu.Hismainresearchinterestsincludedatabaseresearchandnetworkdataprocessing.
Self-AdaptiveClusteringBasedonLocalDensitybyDescendingSearch
XuZhengguo,ZhengHui,HeLiang,andYaoJiaqi
(National Key Laboratory of Science and Technology on Blind Signals Processing, Chengdu 610041)
Clusteranalysisisanimportantresearchdomainofdatamining.Ontheunsupervisedcondition,itisaimedatfiguringouttheclassattributesofsamplesinamixeddatasetautomatically.Fordecadesacertainamountofclusteringalgorithmshavebeenproposedassociatedwithdifferentkindsofprioriknowledge.However,therearestillsomeknottyproblemsunsolvedinclusteringcomplexdatasets,suchastheunknownnumberandmiscellaneouspatternsofclusters,theunbalancednumbersofsamplesbetweenclusters,andvarieddensitieswithinclusters.Theseproblemshavebecomethedifficultandemphaticpointsintheresearchnowadays.Facingthesechallenges,anovelclusteringmethodisintroduced.Basedonthedefinitionoflocaldensityandtheintuitionofordereddensityinclusters,thenewclusteringmethodcanfindoutnaturalpartitionsbyself-adaptedsearchingtheboundariesofclusters.Furthermore,intheclusteringprocess,itcanovercomethestraitenedcircumstancesmentionedabove,withavoidingnoisedisturbanceandfalseclassification.Theclusteringmethodistestifiedon6typicalandmarkedlydifferentdatasets,andtheresultsshowthatithasgoodfeasibilityandperformanceintheexperiments.Comparedwithotherclassicclusteringmethodsandanalgorithmpresentedrecently,inaddition,thenewclusteringmethodoutperformsthemon2differentevaluationindexes.
datamining;clustering;localdensity;descendingsearch;self-adaption
2016-03-10;
2016-06-01
TP391
