一种基于关联信息熵度量的特征选择方法
2016-08-31董红斌滕旭阳
董红斌 滕旭阳 杨 雪
(哈尔滨工程大学计算机科学与技术学院 哈尔滨 150001)
一种基于关联信息熵度量的特征选择方法
董红斌滕旭阳杨雪
(哈尔滨工程大学计算机科学与技术学院哈尔滨150001)
(donghongbin@hrbeu.edu.cn)
特征选择旨在从原始集合中选择一个规模较小的特征子集,该子集能够在数据挖掘和机器学习任务中提供与原集合近似或者更好的表现.在不改变特征物理意义的基础上,较少特征为数据提供了更强的可解读性.传统信息论方法往往将特征相关性和冗余性分割判断,无法判断整个特征子集的组合效应.将数据融合领域中的关联信息熵理论应用到特征选择中,基于该方法度量特征间的独立和冗余程度.利用特征与类别的互信息与特征对组合构建特征相关矩阵,在计算矩阵特征值时充分考虑了特征子集中不同特征间的多变量关系.提出了特征排序方法,并结合参数分析提出一种自适应的特征子集选择方法.实验结果表明所提方法在分类任务中的有效性和高效性.
特征选择;联合信息熵;组合效应;多变量关系;相关矩阵
近年来各行业数据量的指数级增长为数据挖掘与机器学习任务带来了新的挑战.在处理数据量庞大、数据维度高的任务时,首先对数据进行降维是一个行之有效的手段.降维的目的在于用较低维的数据保持原有数据的特性,在完成数据任务时能提供与原数据集近似或更优的表现.目前主流的降维手段有特征提取与特征选择2种[1].特征提取方法将原有特征集合数据转换到一个更低维的新特征空间,主成分分析(principalcomponentanalysis,PCA)和线性判别分析(lineardiscriminantanalysis,LDA)等是特征提取的代表性方法.特征选择则通过一个特定的评估函数来评价特征或特征组合,进而从原始特征集合中选择出一个维度更低的特征子集.两者最本质的区别在于特征选择没有改变原始特征的物理意义,在需要理解数据的潜在意义与原始特性时倾向于使用特征选择方法,在仅需要提供数据辨识能力时倾向于使用特征提取方法.
根据特征子集评估策略的不同,可将特征选择技术大致分为3类[2]:Filter模型、Wrapper模型和Embedded模型.Filter模型仅依赖数据的内在特性来选择特征,而不依赖任何具体的学习算法指导.Wrapper模型则需要一个预先设定的学习算法,将特征子集在其算法上的表现作为评估来确定最终的特征子集.Embedded模型则是在学习算法的目标分析过程中包含变量选择,将此作为训练过程的一部分以获得特征相关性,例如C4.5和LARS方法.Wrapper模型因其高复杂性往往只在具体学习任务中使用.而数据规模庞大时,Filter模型因其高效性和良好的泛化能力则更为理想.根据特征选择的输出结果,又可将特征选择分为特征权重和子集选择2类方法.特征权重方法根据评估函数得出的特征重要程度对其进行排序,具体选择多少特征需要人工控制.子集选择方法则根据对子集的整体评估,输出评估最优的特征子集.
特征选择作为一种数据预处理手段近年来被广泛应用到各行各业中,例如社会网络[3]、入侵检测[4]、生物信息[5]、图像分析[6]和自然语言处理[7]等.在大规模数据集中往往存在大量的无关和冗余特征,而特征选择的主要任务则是在选择相关特征的同时去除冗余特征.在选取特征时各种有效的度量手段作为评估函数应用到特征选择中,例如信息论度量、一致性度量、关联度量、依赖性度量和距离度量等.1994年由Battiti[8]提出的MutualInformation特征选择方法衡量特征与类别标签的相关程度,两者的互信息越多,该特征越重要;Yu等人[9]2004年提出的FCBF方法使用了信息论中的对称不确定性来衡量2个特征的相关性,结合Markovblanket技术删除冗余特征;mRMR作为一种经典的信息论特征选择方法在2005年由Peng等人[10]提出,该方法基于互信息计算兼顾特征与类别之间的相关性与特征之间冗余度.以上3种广为流行的特征选择方法在考虑特征冗余程度时,均是比较特征与特征之间成对的冗余性,而没有判断特征加入或删除后特征子集整体组合信息程度的变化.而特征选择过程中,特征的组合效应近年来得到了学者们的重视.Sun等人[11-12]将合作博弈理论中的班次哈弗权力指数以及夏普利值使用到特征选择方法中,用以评估特征在整个特征子集中的组合影响力,然而在创建候选联盟(生成部分可选子集)时耗费了大量的时间.Dong与杨昙等人[13-14]研究使用进化算法和群体智能度量特征子集的组合效应,但算法往往无法形成固定规模的特征子集.文献[15]中段洁与胡清华等人提出基于粗糙集依赖度量的特征子集选择方法.Liu等人[16]基于此考虑了特征加入后子集依赖性的整体变化,结合Markovblanket理论提出一种新的依赖盈余特征选择方法,该方法较合作博弈理论方法时间复杂度降低,但依然相对耗时.ReliefF[17]和CFS-FS[18]则分别是基于距离度量和基于关联度量的2种经典特征选择方法,ReliefF缺乏对特征子集组合效应的度量,CFS-FS则不能有效处理特征间的冗余关系.
关联信息熵的概念来源于多传感器数据融合领域,是一种度量系统冗余信息的方法.由Wang等人[19]提出并利用该技术度量多传感器系统中的重叠和独立信息,该方法将多变量间相关关系的信息度量计算为[0,1]的闭区间范围.事件之间的独立程度越大,冗余程度(重叠)越小,对应的关联信息熵越大.
本文将每一维特征作为一个传感器,为传感器信息度量和特征信息度量之间建模,进而使用关联信息熵度量特征子集的组合效应.有别于传统信息论方法,该方法充分考虑了特征子集中不同特征间的多变量关系,并在结果中同时体现了特征的关联关系和冗余关系.为了验证算法的有效性,实验分别在UCI中小规模数据集和大规模数据集中进行分析,在分类正确率和运行时间上验证了本文所提方法的高效性.
1 预备知识
1.1特征选择概述
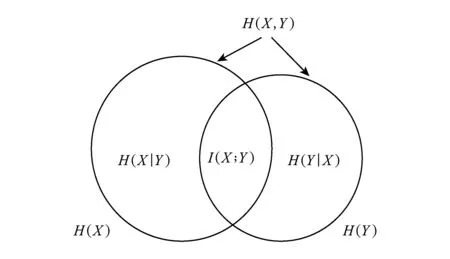
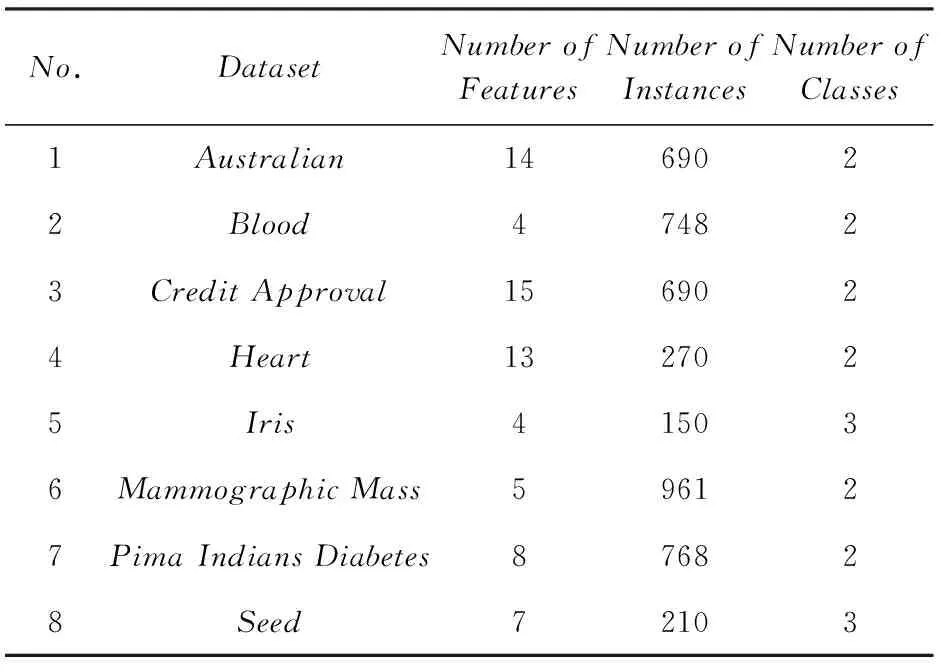
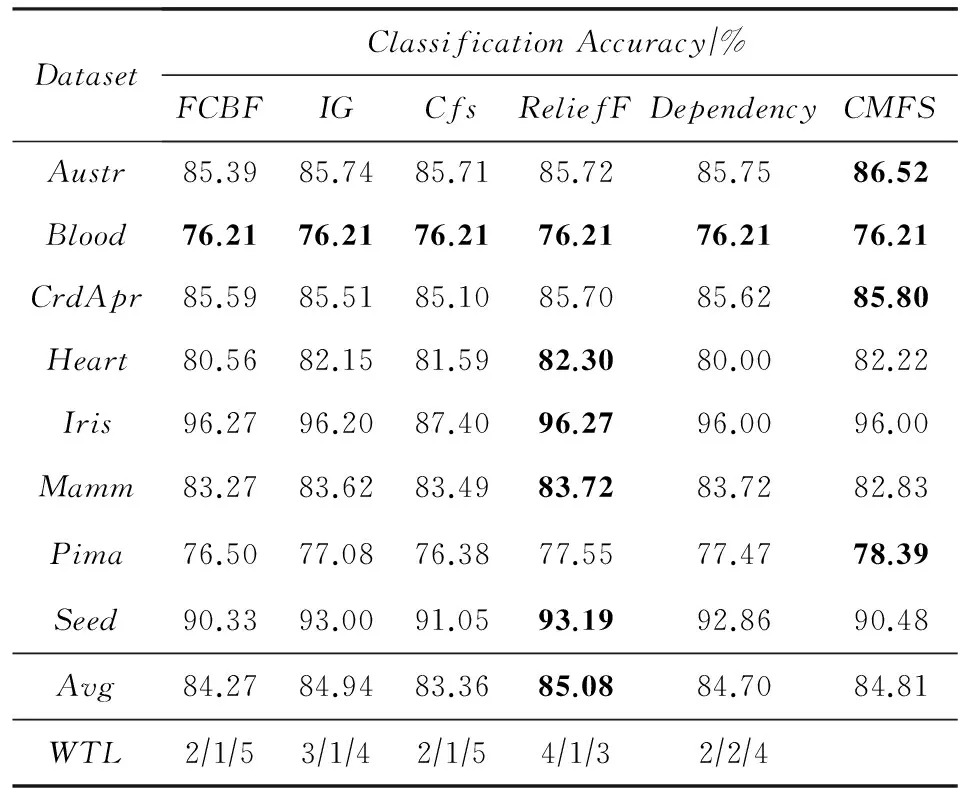
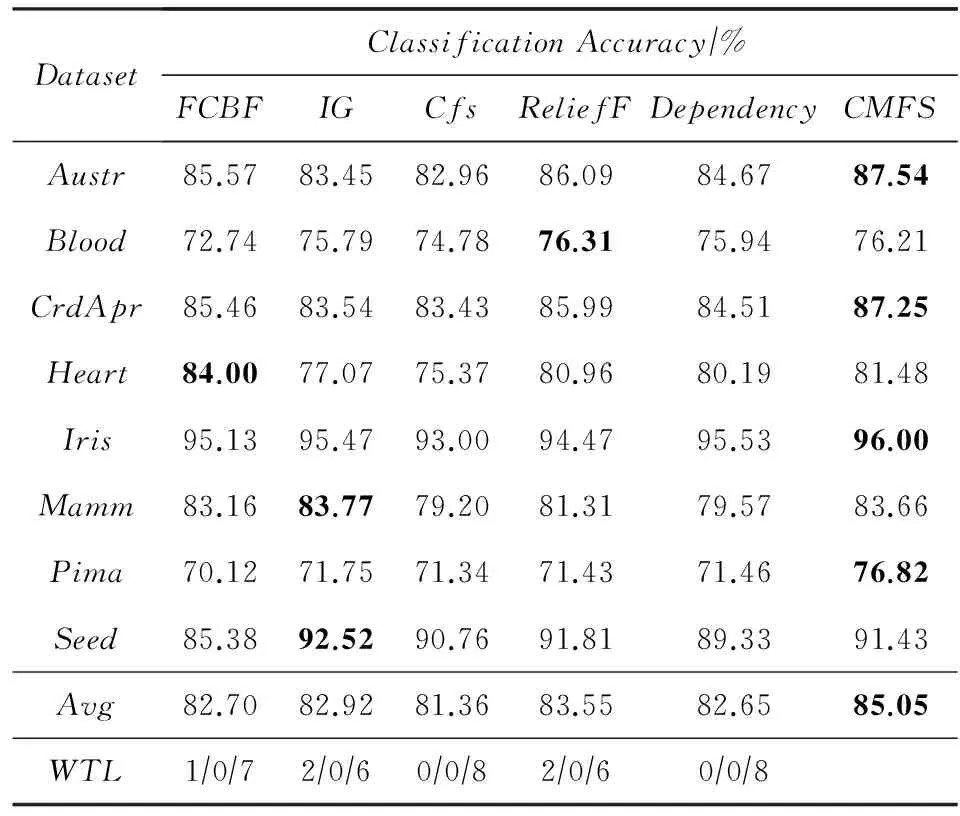
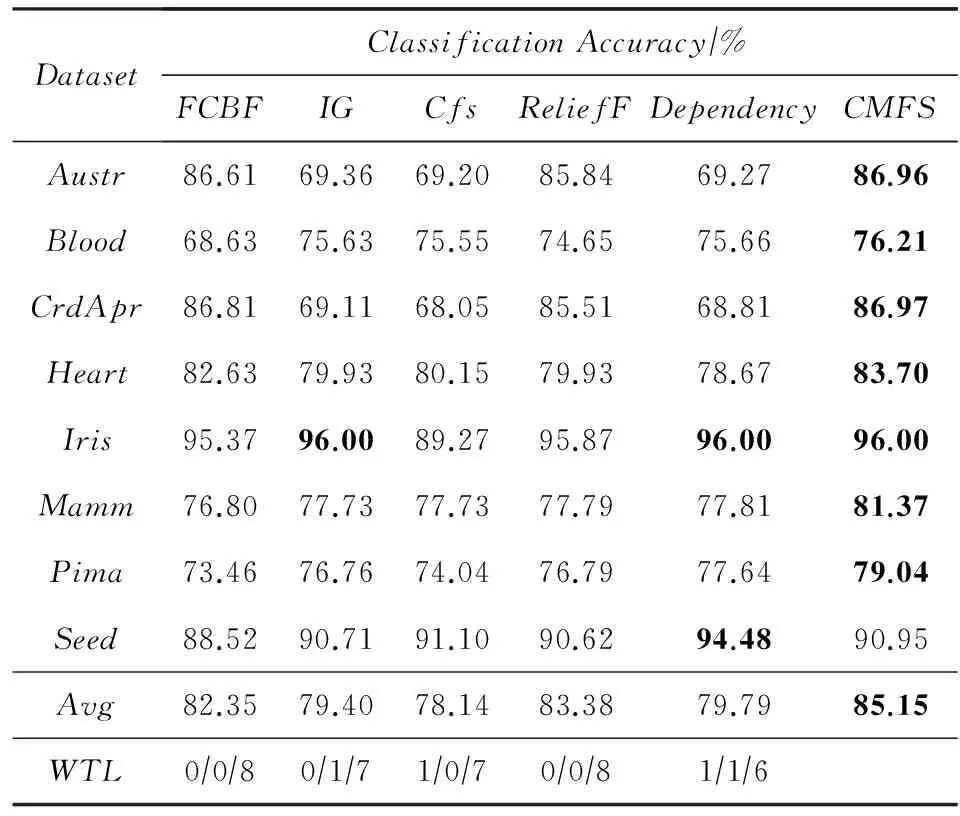
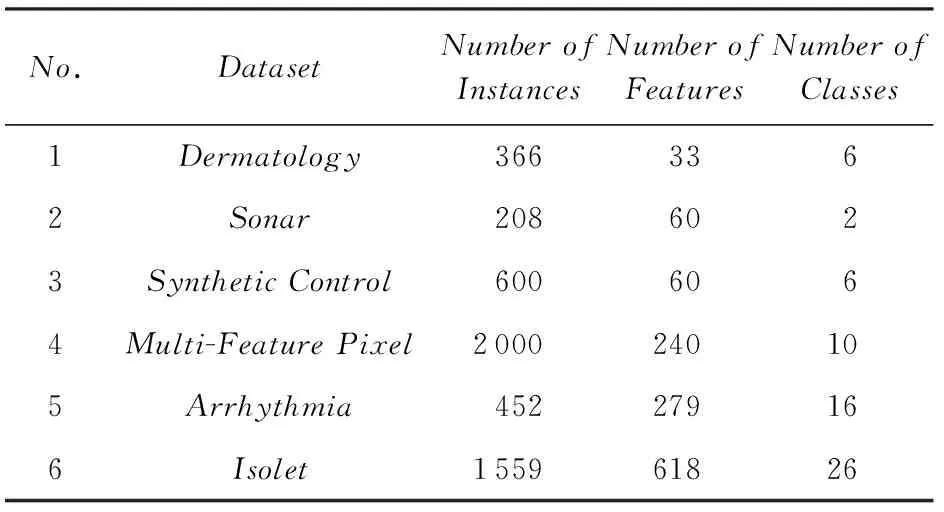
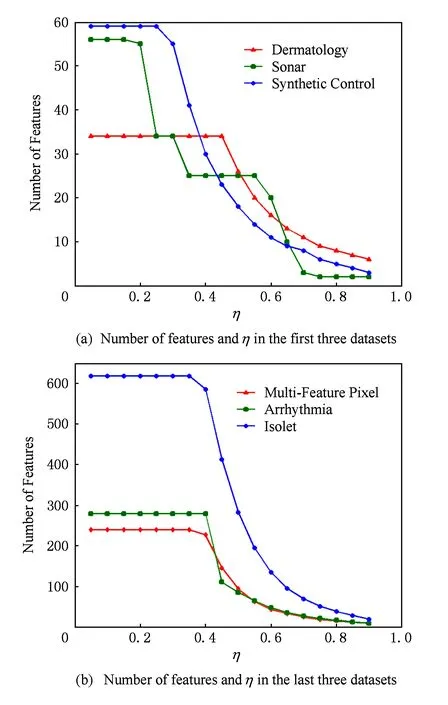
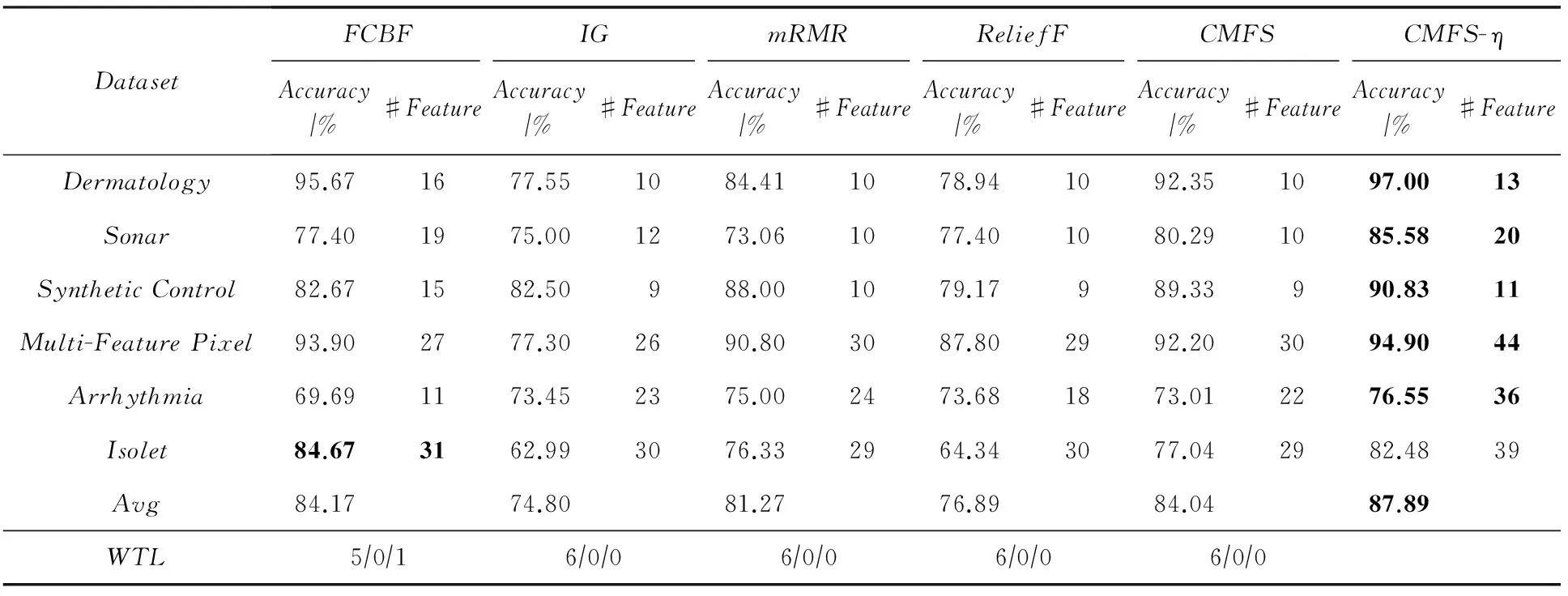
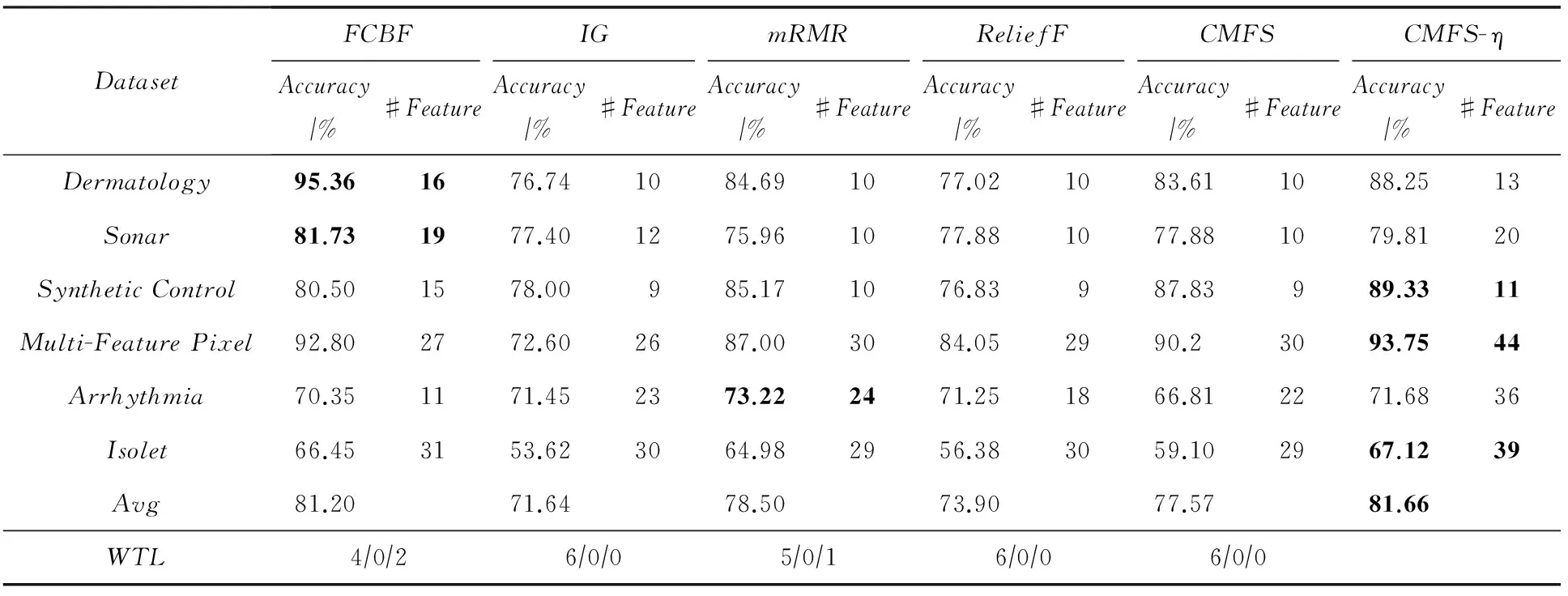
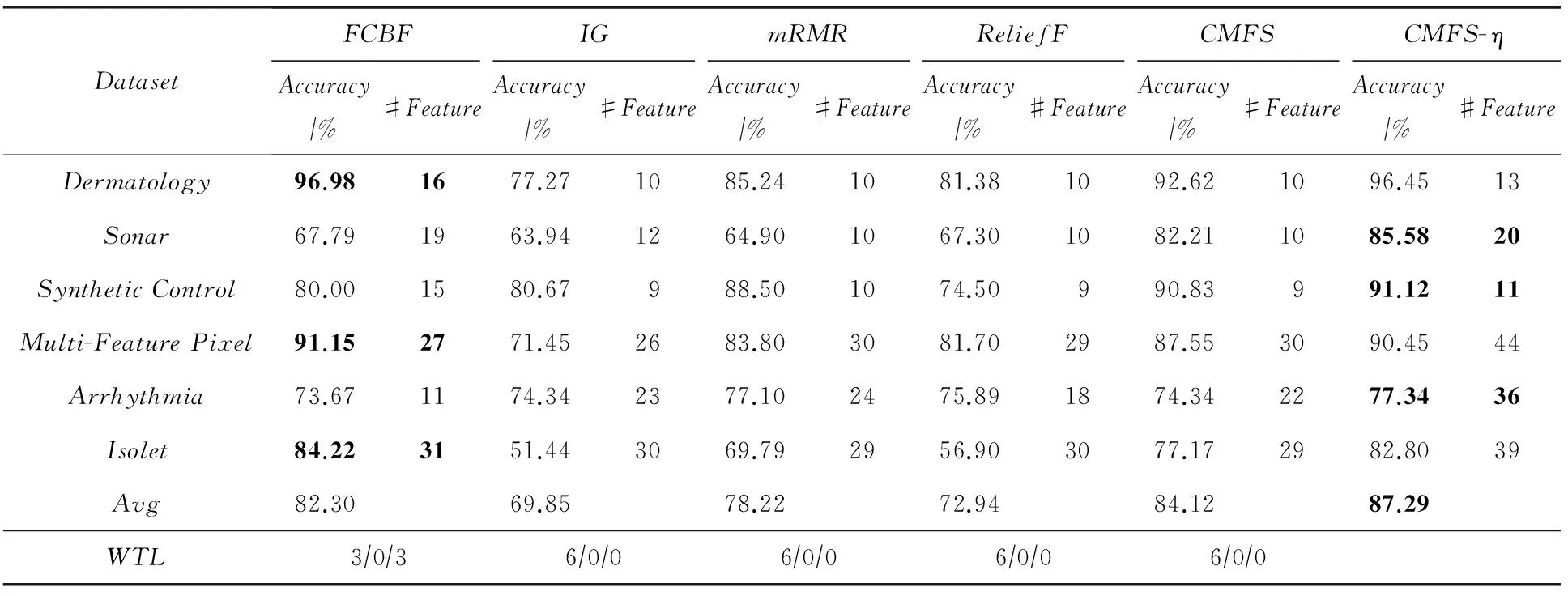
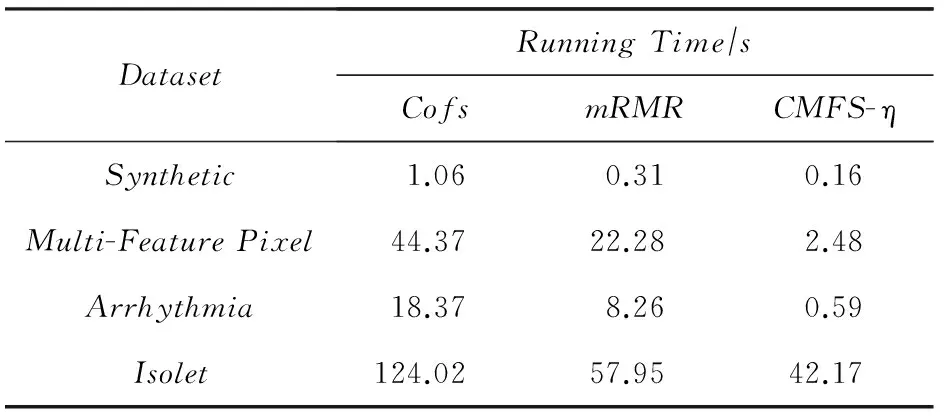
数据集D中含有k个样本D={d1,d2,…,dk},并且对于D中每个样本di都有特征集合X={x1,x2,…,xn},其中包含n维特征,di∈n.对于分类问题,可将D中样本划分为目标集合C中的m个不同的类别C={c1,c2,…,cm}.特征选择的目的是在原始特征集合X中寻找到一个最佳特征子集S,其中S含有p维特征(p 特征选择通常包括4个组件:特征子集生成、子集评估、终止条件和结果验证.基于一个确定的搜索策略,特征子集生成组件首先生成候选特征子集P′;进而使用确定的评估函数对每一个候选特征子集进行度量,并与之前最佳候选特征子集做比较,如果新的特征子集表现更加优越,那么替换原有最佳特征子集.生成和评估过程循环直到满足终止条件.最终所选的特征子集需要用一些给定的学习算法进行结果验证. 1.2互信息原理 在香农的信息熵理论中,熵用于度量随机变量信息的不确定性.H(X)通常用作描述离散随机变量X={x1,x2,…,xn}的熵值,xi是变量X的可能取值,p(xi)为概率密度函数. (1) 当已知2个离散变量X和Y的联合概率密度p(x,y)时,X与Y的联合熵计算为: (2) H(X,Y)=H(X)+H(Y|X)=H(Y)+H(X|Y). (3) 对于给定变量Y,变量X的条件熵将小于或等于其各自单独的熵.当熵值为零时,说明变量X完全依赖变量Y.反之当且仅当2个变量相互独立时,条件熵等于其熵,变量Y对X不提供任何有用信息. (4) 基于以上不确定性的熵值计算,互信息表示2个变量所分享的信息量: I(X;Y)=H(X)-H(Y|X)=H(Y)-H(X|Y)= H(X)+H(Y)-H(X,Y), (5) 当2个变量的互信息值越大,则意味着2个变量相关程度越紧密;当互信息为0时,则意味着2个变量完全不相关,如图1所示[20]: Fig. 1 Relationships between entropy and mutual information.图1 熵与互信息的关系图 1.3关联信息熵理论 假设一个多变量系统具有n个变量,该系统在时刻t(t=1,2,…,m)的多变量时间序列矩阵为P,则有: P=(yi(t))1≤t≤m,1≤i≤n,P∈m×n, (6) 其中,P为实数矩阵,yi(t)表示第i个变量在时刻t的取值.通过对矩阵P进行中心化和标准化处理后得到多变量时间序列矩阵Q: (7) 计算相关矩阵R: R=QTQ,R∈m×n. (8) 对于n个传感器的关联矩阵R可以推导为如下: (9) 1) (10) 2) (11) 每个传感器对系统整体信息的贡献可用其特征值表示.依据信息论计算原理,关联信息熵的计算如下: (12) 因单位阵I的特征值均为1,根据熵计算式(12)可计算HI=1.故: (13) 本文研究从特征选择的基本要求入手,兼顾特征与类别间的相关性以及特征与特征间的冗余性.文章的模型构建将原始特征空间作为多传感器系统,将每一维特征作为一个传感器,在该环境中使用关联信息熵度量来判断特征之间的组合效应,减少特征之间的冗余信息.基于这种度量,本节将提出一种特征排序算法(featuresortingbasedoncorrelationinformationentropymeasurement,CMFS),进而将重叠信息进行阈值η调控,设计一个自适应子集规模的特征选择方法(adaptivefeaturesubsetselectionalgorithmbasedoncorrelationinformationentropymeasurementandη,CMFS-η). 2.1模型描述 原始特征集合X={x1,x2,…,xn}作为含有n个变量的多变量系统,其中每个特征xi等价于一个传感器.这里不同于原传感器系统,本文不使用样本在n维特征下的具体数据作为输入,而是将样本的类别信息C={c1,c2,…,cm}作为系统的时间序列.基于特征与样本类别间的相关性,构造一个可度量的多元变量模型F,此处F等价于1.3节中的矩阵P的转置,具体形式为 矩阵中元素Ii j是每一个特征与相应类别的互信息: I(xi;cj)=H(xi)+H(cj)-H(xi,cj). (14) 由于关联信息度量侧重于考虑多变量之间的冗余(重叠)关系,因此如果将样本在每一维特征下的数据作为输入,无法兼顾特征与类别之间相关性的度量.在高维多样本的空间中,本模型的构建不仅将互信息作为信号输入度量了特征相关性,而且能大大缩减多变量模型的体积,符合特征选择任务的基本要求. (15) (16) 计算特征相关矩阵: (17) 相关矩阵Rel满足对称性,矩阵中的每一个元素代表2个特征在相同类别信息下的相似度. 该过程首先将k×n的原始数据空间压缩为m×n(m≪n,n≪k )的矩阵,虽然在计算特征相关矩阵时矩阵维度升至n×n,但仍大大缩减了数据空间. 2.2特征排序算法CMFS 从线性空间的角度看,在一个定义了内积的线性空间里,对一个n阶对称方阵进行特征分解,就是产生了该空间的n个标准正交基,然后把矩阵投影到这n个基上.n个特征向量就是n个标准正交基,而特征值的规模则代表矩阵在每个基上的投影长度.特征值越大说明矩阵在对应的特征向量上方差越大、功率越大.在数据挖掘的任务中,最大特征值对应的特征向量方向上包含最多的信息量.本文所使用的关联信息熵上从特征集合的角度判断其组合效应,由特征集合得到特征值计算出的关联信息熵判断了特征组合所包含的信息量,同时也度量了特征间的冗余. CMFS算法使用关联信息熵作为子集评估组件,搜索方式采用序列搜索.与传统的序列算法流程不同的是,所提方法首先使用反向删除的策略,选取第1个特征.基于第1个特征,再使用正向添加的策略,对特征集合进行扩充排序.在序列搜索特征选择的过程中,第1个特征的确定起着非常重要的作用,基于互信息的方法,例如:MIFS,mRMR,MIFS-U等都是将与类别互信息最大的特征作为第1个特征放入集合.该方式忽略了特征间的组合效应,而本文从整体获得该特征与整体失去该特征的关联信息熵变化出发,选取特征缺失后使整体冗余信息增量最大的作为第1个特征,特征的选取方式如下: Info(i)= Hall-Hmiss(xi), (18) Hall为全体特征下的关联信息熵,Hmiss(xi)为失去特征xi的关联信息熵. 引理1. 若xi=argmax(Info(i)),特征xi为整体提供最多信息. 整体集合在失去特征xi后冗余信息量上升最大,证明xi与其余特征整体相关,为整体提供了最多信息. 证毕. 假设已排序的特征集合为S,则未排序特征集合为X-S.对于xi∈X-S,添加特征xi到集合S中,扩充后的相关矩阵记为Reladd,计算扩充集合的关联信息熵: (19) 引理2. xi=argmax(Hadd(i)),特征xi为当前排序特征集合提供最多信息. 添加该特征后,当前排序特征集合获得了最少量的冗余信息,获得最大量的差异信息. 证毕. 反向删除是为了确保第1个特征与整体相关,而非冗余特征.而正向扩充的目的是为了确保在排序后的特征集合中选取任意p>1个特征构成的特征集合是低冗余高相关.具体过程如算法1所示: 算法1. 关联信息熵度量的特征排序算法. 输入:数据集D、特征集合X、类别信息C; 输出:排序后的特征集合S. ① S=∅; ②Foreachxi∈X,cj∈C ③ 根据式(14)计算Ii j,得到矩阵F; ④EndFor ⑤ 根据式(15)(16)进行中心化和标准化得到矩阵QF; ⑥ 根据式(17)得到特征相关矩阵Rel; ⑧Foreachxi∈X ⑨ 根据式(18)计算Info(i); ⑩EndFor 2.3自适应子集选择方法CMFS-η 该部分考虑引入阈值η 进行子集规模的控制,简称为CMFS-η.不同于传统的特征个数阈值,η的引入是从信息度量的角度进行控制: (20) 由式(20)看出,η是对冗余信息的控制,该参数仍然确保每次加入的特征带来了最低的冗余信息,但当带来的冗余信息超出1-η的限定时,算法终止迭代.至此,算法再添加剩余特征中的任何特征都将带来高于1-η的冗余信息.因此该过程可自适应地形成子集规模,无需特征个数的硬划分,并确保了冗余信息尽可能少.具体过程如算法2所示: 算法2. 关联信息熵度量的自适应特征选择算法. 输入:数据集D、特征集合X、类别信息C; 输出:排序后的特征集合S. 对于η 的具体取值,将在实验部分进行详细分析. 2.4计算复杂度分析 为了验证本文提出算法的高效性,本文选择了UCI数据集中14个数据集,采用4个部分进行验证:1)针对特征维度适中,样本与类别数目较少的数据集进行实验分析,验证本文所提排序算法在手动设置特征子集规模下的有效性;2)对η在高维数据集中的表现进行分析,判断其在控制特征规模与分类正确率2方面的表现,得到相应阈值;3)在高维样本数据集下验证所提CMFS与CMFS-η的有效性;4)给出时间效率的对比.本文实验特征排序与子集选择部分的运行环境为Matlab2013a,分类正确率运行环境为weka3.7.对数据的离散化处理采用经典的MDL方法[21].部分实验结果参见文献[14,22]. 3.1CMFS算法在中小规模数据中的结果分析 本部分选用8个UCI数据集进行验证,数据集各项指标如表1所示: Table 1 Descriptions of UCI Benchmark Datasets表1 UCI数据集描述 实验对比的特征选择方法有FCBF,IG,Cfs,ReliefF,Dependency.以上方法分别是信息熵特征选择、基于关联性特征选择、基于距离度量特征选择以及基于一致性度量特征选择的代表性算法.为了验证算法性能,选取SVM,CART,NaïveBayes三个分类器使用10折交叉验证对选择的特征进行分类测试,取最优结果.本文所提CMFS方法在本部分实验中对8个数据集的特征进行排序,最终手动选择5,1,5,7,2,2,5,5个特征,平均约减了53.5%的数据规模.具体的分类结果如表2~4所示.表中数值数据表示各特征选择方法选择的特征子集在相应数据集下使用分类器得到的分类正确率,其中加粗数据表示为该行分类效果最高正确率,Avg行的表示平均分类正确率.表格最后一行WTL表示该列方法与所提出CMFS方法相比在8个数据集上Win(胜于)Tie(平手)Lose(弱于)的次数.表格中对部分数据集进行简称:Austr,CrdApr,Mamm,Pima分别为对应表1中的1,3,6,7个数据集. Table 2 Classification Accuracy with SVM Classifiers表2 SVM分类器的分类正确率 Table 3 Classification Accuracy with CART Classifiers表3 CART分类器的分类正确率 Table 4 Classification Accuracy with Naïve Bayes Classifiers表4 Naïve Bayes分类器的分类正确率 从表2中可以看到,所提方法在SVM分类器下分别在Austr,CrdApr,Pima数据集中取得了最好的分类正确率.在Blood数据集与其他特征选择方法获得了相同的分类正确率.在Heart数据集中仅落后ReliefF方法0.08%.在该分类器下CMFS没有取得最高平均分类正确率,弱于最优0.27%,但是在WTL指标中除弱于ReliefF方法,均优于其他方法,平均获得了52.5%的胜率. 所提方法在CART分类器下的表现优于在SVM分类器下的表现,如表3所示.在各个特征选择方法选择与表2相同的特征子集空间中,CMFS在该分类器下取得了最好的平均分类正确率,并高于次优1.5%.从表3中可看到所提方法在Austr,CrdApr,Iris和Pima数据集中取得了最好的分类正确率.在Blood数据集中,所提方法比ReliefF落后0.1%的正确率,在Mamm数据集中落后最优0.11%.WTL指标中均优于其他方法,平均获得了87.5%的胜率. CMFS在NaïveBayes分类器下仍然保持优势,在前7个数据集中均取得了最高的分类正确率.并且平均正确率高于第2名1.77%.在WTL指标中均优于其他方法,平均获得了90%的胜率,如表4所示. 本部分实验结果验证了所提CMFS方法虽然在SVM分类器下性能非最佳,但仍然取得了较高的分类正确率和胜率.综合其在3个分类器下的表现,验证了CMFS算法在非高维中小规模数据集下的有效性. 3.2η参数的性能分析 本部分实验将通过对超高维数据集上的运行,分析η参数的合理取值范围.在中小规模数据集中,算法运行时间短,η的意义不显著.而在超高维数据中,η的调控将在迭代扩充特征的过程中缩减大量的运行时间.所选取的超高维UCI数据集如表5所示,数据维度从33维升至618维. Table 5 Descriptions of UCI Benchmark Datasets表5 UCI数据集描述 η调控的意义在于既保证特征维度的降低,又要保证较高的分类正确率.因此实验将对这2方面进行分析. 为确保参数的泛化效果,本文将采用SVM,1-NN,NaïveBayes三种分类器上的平均分类正确率作为参考,结果如图2,3所示: Fig. 2 The relationship between number of features and parameter η.图2 特征维度与参数η的关系图 1) 维度的比较.从图2(a)与图2(b)中可以看出参数η对特征子集的规模有一个较好的控制,η=0.1时,在算法2中意味着允许加入的特征带了0.9的冗余信息,对冗余信息的限定较低所以图中看出,特征子集规模等于特征原始集合规模,此时方法相当于特征排序算法.随着η数值的升高,冗余扩充特征带来的冗余信息少于1-η,特征子集规模将变得越来越小.6个数据集中,η>0.4时,特征子集规模均缩小.而0.6≤η≤0.7时,特征数目对比原特征集合已经有了巨幅缩减,并趋于平稳态势.η>0.7时,意味着仅允许特征带来0.3的冗余,特征子集规模变化较小. 2) 平均分类正确率的比较.在噪声较小的数据集中,随着特征子集规模的减小,平均分类正确率也会随之下降.在噪声较多的数据集中,例如:Sonar和Arrhythmia,平均分类正确率会随着删除无关与冗余特征先升高再下降,如图3所示.对比参数与维度的关系,当η<0.35时,除Sonar数据集(在图2(a)中,特征维度此处有较大变化),平均分类正确率等同于原有特征集合.当0.6≤η≤0.7时,平均分类正确率在噪声较小的数据集中,有小幅度下滑;在噪声较多的数据集中平均分类正确率有显著提升.当η>0.7时,各个数据集上的正确率则有显著的下滑趋势. Fig. 3 Relationship between average classification accuracy and parameter η .图3 平均分类正确率与参数η的关系图 综合上述分析,当0.6≤η≤0.65时可大大缩减特征子集规模同时保证较高的平均分类正确率.该参数为自适应特征子集规模提供了指导.其优势将继续在实验3.3节中说明. 3.3CMFS与CMFS-η在高维数据中的表现 本部分选取的实验数据集为3.2节中介绍的6个超高维数据集.为了验证算法的泛化能力,本部分将3.1节中的特征选择对比算法与分类器进行部分调整.选择了FCBF,IG,ReliefF,mRMR这4种方法,选取了SVM,1-NN,NaïveBayes三种分类器,分类时依然采用10折交叉验证.具体分类正确率的实验结果如表6~8所示.本部分实验增加了选择特征个数的对比,#Feature为特征选择后特征子集的规模.为了公平对比,CMFS算法选择与其他算法几乎同等规模的子集进行对比,而CMFS-η算法根据3.2节实验结果,取值0.6≤η≤0.65自适应选择子集规模.但由于Isolet为超高维数据集,虽然在自适应算法η=0.65时分别取得了88.17%,78.02%,90.96%的平均分类正确率并大大优于其他方法,但形成的特征子集规模较大,为了保证公平性此数据集中η=0.8,以获得相似规模的特征子集.在其余5个数据集的自适应算法中η=0.65.其中FCBF与CMFS-η为子集选择算法,而IG,ReliefF,mRMR,CMFS为特征排序算法.由于子集选择算法选择的子集规模比排序算法手动限制规模大,因此分类性能会优于排序算法.具体结果如表6~8所示. Table 6 Comparison of Classification Accuracy and Number of Features with SVM Classifiers表6 SVM分类器的分类正确率与特征数目对比 Table 7 Comparison of Classification Accuracy and Number of Features with 1-NN Classifiers表7 1-NN分类器的分类正确率与特征数目 Table 8 Comparison of Classification Accuracy and Number of Features with Naïve Bayes Classifiers表8 Naïve Bayes分类器的分类正确率与特征数目 表6是各个特征选择算法在SVM分类器上的表现,可以看出CMFS-η在5个数据集上均取得了最高的分类正确率,并且取得了最高的平均分类正确率.在Isolet数据集中算法获得了第二高的平均分类正确率,仅比FCBF算法少了2.19%.CMFS-η获得了96.67%的胜率.CMFS方法在SVM分类器上的表现也十分优异,平均正确率仅比FCBF算法少了0.13%,并且在3个数据集中获得了次优的正确率,而且算法本身选择限定的特征子集规模除Arrhythmia数据集外均小于FCBF所选择的子集规模.CMFS方法在5个数据集中的表现均优于IG,ReliefF,mRMR这3种特征排序方法,在Arrhythmia数据集中选择比IG算法少一个特征的情况下,分类正确率仅落后0.44%.在1-NN分类器中,CMFS-η依然保持着最佳的平均分类正确率,结果如表7所示.算法在Syntheticcontrol,Multi-featurepixel,Isolet这3个数据集上取得了最佳分类效果.在其他3个数据集中取得了第2名的分类效果,整体胜率为90%.CMFS在该分类器下表现整体优于IG,ReliefF算法,但稍弱于mRMR方法,整体平均正确率落后0.93%.尽管如此,CMFS在Sonar,Syntheticcontrol,Multi-featurepixel这3个数据集上也取得优于mRMR方法的分类正确率. 对比表8中NaïveBayes分类器的实验结果,可以看出CMFS-η的在分类任务中的优势,整体平均正确率比第2名的FCBF算法高出4.99%.在Sonar,Syntheticcontrol,Arrhythmia数据集上取得了最佳分类效果.在其余3个数据集中也取得了与FCBF近似的正确率,并获得90%的胜率.CMFS算法在此分类器表现优于IG,ReliefF,mRMR算法,并在5个数据集中上均保持优于3种算法的分类正确率. 通过上述实验分析在子集选择方法中,CMFS-η方法优于FCBF方法;在特征排序算法中,提出的CMFS方法优于IG,ReliefF,mRMR算法.整体效果本文提出的CMFS-η最优. 3.4算法时间对比 Cofs是文献[11]中提出的基于合作博弈的特征选择方法,该方法充分考虑了特征的组合效应,并取得了非常优秀的分类性能,然而该方法时间复杂度高,在每次生成候选特征子集时算法时间复杂度呈指数级,导致耗时较多.mRMR方法与本文所提算法时间复杂度接近,因此本部分选取这2种方法进行运行时间对比.为对比效果差异,在同样环境设置中选取4个维度递增的高维数据集运行3种算法.具体结果如表9所示: Table 9 Running Time on UCI Datasets表9 在UCI数据集上运行时间对比 通过1.4节分析,提出算法的时间复杂度对样本维度依赖较高,而对样本数目依赖较小.mRMR方法不仅对特征维度依赖较高,对样本数目依赖程度更高.从表9中数据得出,CMFS-η算法运行时间最快.在Synthetic数据集中,样本数为特征维度的10倍,CMFS-η算法的运行时间0.16s,约为mRMR算法的12,约为Cofs算法的17.在Multi-featurepixel数据集中,样本数约为特征维度的8倍,CMFS-η算法的运行时间约为mRMR算法的110,约为Cofs算法的120.由于Arrhythmia数据集中存在大量取值相同的特征,因此在计算之时已经减少了特征维度,所以在该数据集中,CMFS-η算法的运行时间更具优势,约为mRMR算法的7100,约为Cofs算法的3100.在Isolet数据集中CMFS-η算法的运行时间约为Cofs算法13,仅比mRMR算法少约16s.这是因为Isolet是超高维数据,而且样本数目约为2.5倍,因此CMFS-η算法运行时间相对较少,但不会出现成倍缩减,符合前文对时间复杂度的分析.综上,在样本数远远大于其样本维度时,本文算法优势将变得更加明显. 本文针对特征成组后缺少组合效应度量的问题,研究了多传感器领域中的关联信息熵的性质,并将其引入到特征选择任务中,完成其模型的映射与构建.基于关联互信息本文提出了特征排序算法CMFS与自适应子集选择算法CMFS-η,给出了算法复杂度分析,证明其优于典型的mRMR算法.通过在不同规模数据集上的实验,验证了所提算法的有效性和高效性.在中小规模数据集中通过手动限定特征个数,CMFS方法获得了6种算法中的最佳平均分类正确率.通过对参数η在特征维度与分类正确率2方面的讨论与设置,CMFS-η算法自适应选择子集并在大规模高维数据集中获得了整体平均92.22%的胜率.实验最后给出了运行时间,对比表明算法任务执行的效率. 本文提出的特征选择方法在分类精度和运行速度上具备良好的性能,对于处理大规模数据的实际问题具有应用价值.但本文选取的是单标签数据集进行分类任务的比较,未来将进行多标签数据集标签成组相关性和特征与多标签相关性的研究,比较单标签与多标签在度量冗余信息时的差异. [1]BennasarM,HicksY,SetchiR.Featureselectionusingjointmutualinformationmaximisation[J].ExpertSystemswithApplications, 2015, 42(22): 8520-8532 [2]ZhaoZheng,MorstatterF,SharmaS,etal.Advancingfeatureselectionresearch-ASUfeatureselectionrepository[R].Phoenix,AZ:SchoolofComputing,Informatics,andDecisionSystemsEngineering,ArizonaStateUniversity,Tempe, 2010 [3]TangJiliang,LiuHuan.Unsupervisedfeatureselectionforlinkedsocialmediadata[C] //Procofthe18thACMSIGKDDIntConfonKnowledgeDiscoveryandDataMining.NewYork:ACM, 2012: 904-912 [4]EesaAS,OrmanZ,BrifcaniAMA.Anovelfeature-selectionapproachbasedonthecuttlefishoptimizationalgorithmforintrusiondetectionsystems[J].ExpertSystemswithApplications, 2015, 42(5): 2670-2679 [5]SaeysY,InzaI,LarraagaP.Areviewoffeatureselectiontechniquesinbioinformatics[J].Bioinformatics, 2007, 23(19): 2507-2517 [6]SinghD,GnanaAA,BalamuruganS,etal.Anovelfeatureselectionmethodforimageclassification[J].OptoelectronicandAdvancedMaterials-RapidCommunications, 2015, 9(11//12): 1362-1368 [7]MengJiana,LinHongfei,YuYuhai.Atwo-stagefeatureselectionmethodfortextcategorization[J].Computers&MathematicswithApplications, 2011, 62(7): 2793-2800 [8]BattitiR.Usingmutualinformationforselectingfeaturesinsupervisedneuralnetlearning[J].IEEETransonNeuralNetworks, 1994, 5(4): 537-550 [9]YuLei,LiuHua.Efficientfeatureselectionviaanalysisofrelevanceandredundancy[J].TheJournalofMachineLearningResearch, 2004, 5: 1205-1224 [10]PengHanchuan,LongFuhui,DingC.Featureselectionbasedonmutualinformationcriteriaofmax-dependency,max-relevance,andmin-redundancy[J].IEEETransonPatternAnalysisandMachineIntelligence, 2005, 27(8): 1226-1238 [11]SunXin,LiuYanheng,LiJin,etal.Usingcooperativegametheorytooptimizethefeatureselectionproblem[J].Neurocomputing, 2012, 97: 86-93 [12]SunXin,LiuYanheng,LiJin,etal.Featureevaluationandselectionwithcooperativegametheory[J].PatternRecognition, 2012, 45(8): 2992-3002 [13]DongHongbin,TengXuyang,ZhouYang,etal.Featuresubsetselectionusingdynamicmixedstrategy[C] //Procof2015IEEECongressonEvolutionaryComputation.Piscataway,NJ:IEEE, 2015: 672-679 [14]YangTan,FengXiang,YuHuiqun.Featureselectionalgorithmbasedonthemulti-colonyfairnessmodel[J].JournalofComputerResearchandDevelopment, 2015, 52(8): 1742-1756 (inChinese) (杨昙, 冯翔, 虞慧群. 基于多群体公平模型的特征选择算法[J]. 计算机研究与发展, 2015, 52(8): 1742-1756) [15]DuanJie,HuQinghua,ZhangLingjun,etal.Featureselectionformulti-labelclassificationbasedonneighborhoodroughset[J].JournalofComputerResearchandDevelopment, 2015, 52(1): 56-65 (inChinese) (段洁, 胡清华, 张灵均, 等. 基于邻域粗糙集的多标记分类特征选择算法[J]. 计算机研究与发展, 2015, 52(1): 56-65) [16]LiuYong,TangFeng,ZengZzhiyong.Featureselectionbasedondependencymargin[J].IEEETransonCybernetics, 2015, 45(6): 1209-1221 [17]Robnik-ikonjaM,KononenkoI.TheoreticalandempiricalanalysisofReliefFandRReliefF[J].MachineLearning, 2003, 53(1//2): 23-69 [18]HallMA.Correlation-basedfeatureselectionfordiscreteandnumericclassmachinelearning[C] //Procofthe17thIntConfofMachineLearning(ICML).SanFrancisco:MorganKaufmann, 2000: 359-366 [19]WangQiang,ShenYi,ZhangYe,etal.Fastquantitativecorrelationanalysisandinformationdeviationanalysisforevaluatingtheperformancesofimagefusiontechniques[J].IEEETransonInstrumentationandMeasurement, 2004, 53(5): 1441-1447 [20]WangZhichun,LiMinqiang,LiJuanzi.Amulti-objectiveevolutionaryalgorithmforfeatureselectionbasedonmutualinformationwithanewredundancymeasure[J].InformationSciences, 2015, 307: 73-88 [21]FayyyadUM,IraniKB.Multi-intervaldiscretizationofcontinuous-valuedattributesforclassificationlearning[C] //Procofthe13thIntJointConfonArtificialIntelligence.SanFrancisco,CA:MorganKaufmann, 1993: 1022-1027 [22]SunXin,LiuYanheng,XuMantao,etal.Featureselectionusingdynamicweightsforclassification[J].Knowledge-BasedSystems, 2013, 37: 541-549 DongHongbin,bornin1963.ProfessorandPhDsupervisorinHarbinEngineeringUniversity.Hismainresearchinterestsincludemulti-agentsystemandmachinelearning. TengXuyang,bornin1987.PhDcandidateinHarbinEngineeringUniversity.Hismainresearchinterestsincludemachinelearningandintelligentinformationprocessing. YangXue,bornin1986.PhDcandidateinHarbinEngineeringUniversity.Hermainresearchinterestsincludeintelligentoptimizationalgorithmandauctiononlineadvertising. FeatureSelectionBasedontheMeasurementofCorrelationInformationEntropy DongHongbin,TengXuyang,andYangXue (College of Computer Science and Technology, Harbin Engineering University, Harbin 150001) Featureselectionaimstoselectasmallerfeaturesubsetfromtheoriginalfeatureset.Thesubsetcanprovidetheapproximateorbetterperformanceindataminingandmachinelearning.Withouttransformingphysicalcharacteristicsoffeatures,fewerfeaturesgiveamorepowerfulinterpretation.Traditionalinformation-theoreticmethodstendtomeasurefeaturesrelevanceandredundancyseparatelyandignorethecombinationeffectofthewholefeaturesubset.Inthispaper,thecorrelationinformationentropyisappliedtofeatureselection,whichisatechnologyindatafusion.Basedonthismethod,wemeasurethedegreeoftheindependenceandredundancyamongfeatures.Thenthecorrelationmatrixisconstructedbyutilizingthemutualinformationbetweenfeaturesandtheirclasslabelsandthecombinationoffeaturepairs.Besides,withtheconsiderationofthemultivariablecorrelationofdifferentfeaturesinsubset,theeigenvalueofthecorrelationmatrixiscalculated.Therefore,thesortingalgorithmoffeaturesandanadaptivefeaturesubsetselectionalgorithmcombiningwiththeparameterareproposed.Experimentresultsshowtheeffectivenessandefficiencyonclassificationtasksoftheproposedalgorithms. featureselection;correlationinformationentropy;groupeffect;multivariablecorrelation;correlationmatrix 2016-03-17; 2016-05-30 国家自然科学基金项目(61472095,61502116);黑龙江省教育厅智能教育与信息工程重点实验室开放基金项目 滕旭阳 (teng_xuyang@126.com) TP18 ThisworkwassupportedbytheNationalNaturalScienceFoundationofChina(61472095, 61502116)andtheOpenFoundationoftheHeilongjiangProvincialEducationDepartmentKeyLaboratoryofIntelligentEducationandInformationEngineering.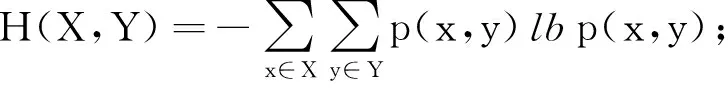
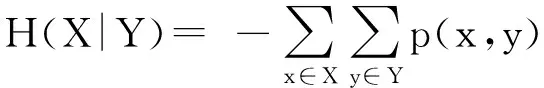
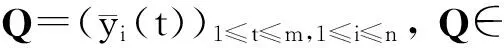
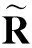
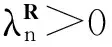
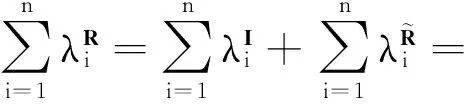
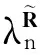
2 使用关联信息熵度量的特征选择方法
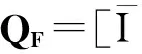
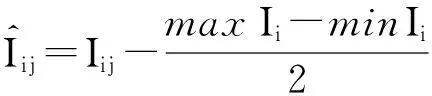
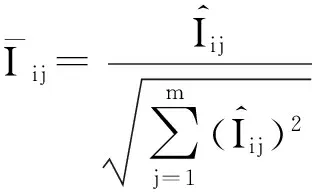
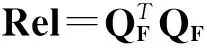
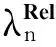
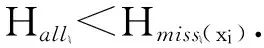
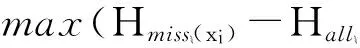
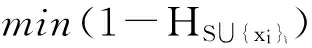
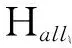
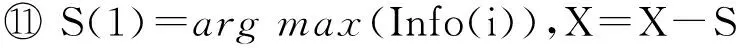

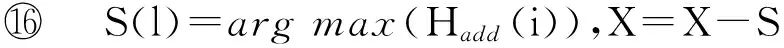

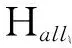
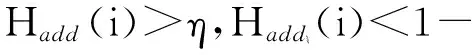
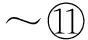


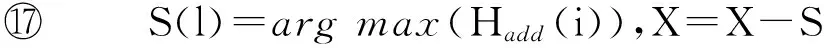


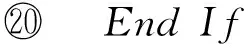

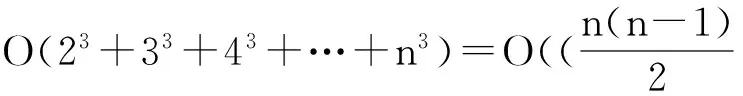
3 实验结果与分析

4 结束语



