基于层次分析法的指挥信息系统效能评估

苏耀峰

基于层次分析法的指挥信息系统效能评估

苏耀峰

为了对指挥信息系统效能进行评估验证，首先对层次分析法的基本思想和评估步骤进行了分析，然后从构建效能评估指标体系、建立递阶层次结构模型、构造判断矩阵和计算优先数、计算综合优先数和确定排序得出效能评估值等四个步骤验证其在指挥信息系统效能评估中的应用。该方法的应用大大提高了指挥信息系统效能评估的可操作性和科学性。

层次分析法（Analytic Hierarchy Process，AHP）是上世纪七十年代由美国匹兹堡大学运筹学教授Satty提出的一种系统分析方法。它认为一个复杂问题通常可以表示为有序的层次结构，通过建立两两比较矩阵得出各个指标层的相对权重，进而得出系统效能值。该方法以其定性与定量相结合处理各种决策因素的特点，广泛应用于武器装备、水利工程等复杂系统的效能评估。

指挥信息系统是信息化战争的物质基础，在信息化战争中的地位与作用日益突出。指挥信息系统的作战效能与作战背景、作战样式、使命任务、作战对手、系统自身效能等众多因素有关，而且各个因素之间相互影响、相互制约，因此就需要从不同角度运用多种标准进行评估。本文通过对层次分析法的深入分析，利用建立好的评估指标体系，对指挥信息系统效能进行评估验证。

基本思路

层次分析法主要思想是根据待评估系统的功能按照要求达到的目标分为若干组成因素，并依照各个因素之间的隶属关系将其分层，从而构成一个层次结构模型。然后分析每一层因素，计算得出处于低层因素对于目标层的重要性权值，并进行比较排序。在AHP方法中，准则和目标等因素被分为各不关联的层次，并形成自上而下的支配关系，即递阶层次关系。该关系是AHP方法的核心关系，通过分析建立递阶层次结构是否有效合理对于能否成功解决问题具有决定性意义。

使用层次分析法进行评估大致可以分为四个步骤：

（1）界定待评估系统的边界，分析系统各个影响因素的关系，将系统分为不同层次；

（2）比较每一层次中的因素相对于上一层因素的重要性，建立权重判断矩阵；

（3）根据判断矩阵计算得到各层次中的各指标权重，并检验其一致性；

（4）合成计算各层元素对最高层的权重并进行排序。

评估实例

指挥信息系统效能评估是对系统自身功能、质量的评估，即技术性能的评估；是对系统在作战环境中运用效能的评估，即作战效能的评估。指挥信息系统效能评估的步骤通常包括系统界定和状态描述、明确假设条件、建立指标体系、确定评估模型、收集与分析数据、检验评估结论等六个步骤。下面结合层次分析法按照构建效能评估指标体系、建立递阶层次结构模型、构造判断矩阵，计算优先数、计算综合优先数，确定排序等四个步骤验证其在指挥信息系统效能评估中的应用。

构建效能评估指标体系

构建指挥信息系统效能评估指标体系首先需要梳理系统主要功能和战技术指标，然后通过层次结构进行分层描述，进而构成系统整体指标体系。根据指挥信息系统的使命任务，通常认为系统应该具备最基本的八种保障能力，即人机交互能力、信息处理能力、辅助决策能力、系统互通能力、信息传输能力、系统生存能力、情报获取能力、系统安全保密能力。根据上述能力可得出指挥信息系统效能评估的通用指标体系，如图1所示。

建立递阶层次结构模型

层次分析法中递阶层次一般包括方案层、准则层与目标层三个基本层次，结合以上内容构建的指挥信息系统效能评估体系，可以将指挥信息系统效能作为层次结构模型中的目标层；将情报获取能力A1、信息传输能力A2以及其他能力作为层次结构模型中的准则层；共有三套系统参与效能评估，作为方案层。评价层次结构如图2所示。

图1 指挥信息系统效能评估指标体系

表1 准则层的判断矩阵和优先数

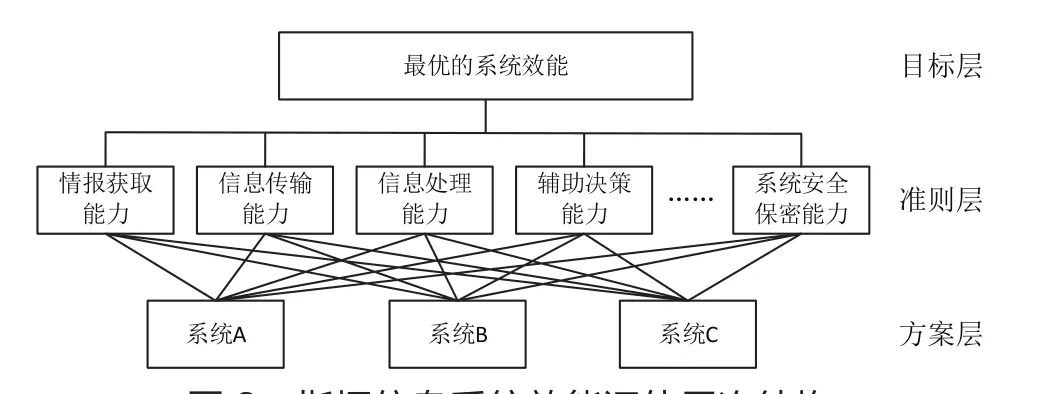
图2 指挥信息系统效能评估层次结构

构造判断矩阵，计算优先数

在某一准则下，对于任意两个元素，通过比较可以得出哪个元素更重要些及重要程度。即，若第个元素与第个元素比较得，则元素与元素比较为，并且有。目前，多使用1～9的比例标度作为赋予重要多少的数值，即两个元素同等重要，标度值为1；两个元素中，元素稍重要，标度值为3；两个元素中，元素更重要，标度值为5；两个元素中，元素有主导作用，标度值为7；两个元素中，元素有强主导作用，标度值为9；其他折中情况，标度值可为2、4、6、8及其他中间值。最终构造出评价指标判断矩阵。

优先数根据上述判断矩阵求出的最大特征根得到对应的单位特征向量，即在某一准则下的排序权重。其计算方法有幂法、和法、根法、最小二乘法、上三角元素法等。本文采用根法计算优先数，即，首先计算判断矩阵每一行元素的乘积，并计算该乘积的n次方根，对所得到的n个n次方根进行归一化处理，即可得到所求的优先数向量。

准则层的判断矩阵和优先数如表1所示。

方案层的判断矩阵和优先数如表2-表9所示。

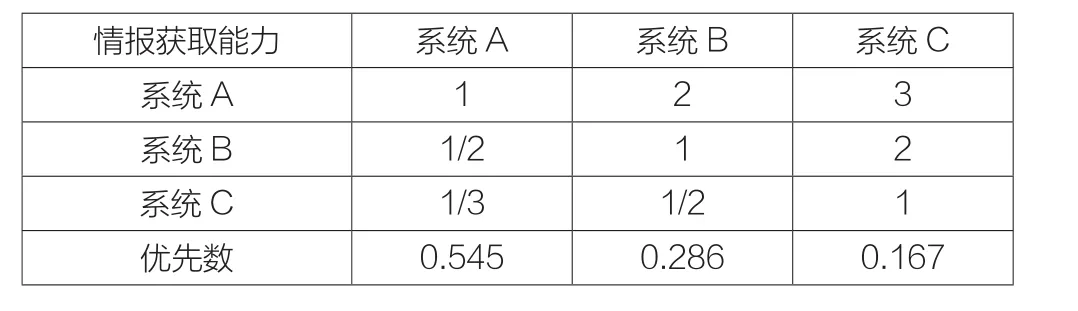
表2 方案层“情报获取能力”判断矩阵和优先数

表3 方案层“信息传输能力”判断矩阵和优先数

表4 方案层“信息处理能力”判断矩阵和优先数

表5 方案层“辅助决策能力”判断矩阵和优先数

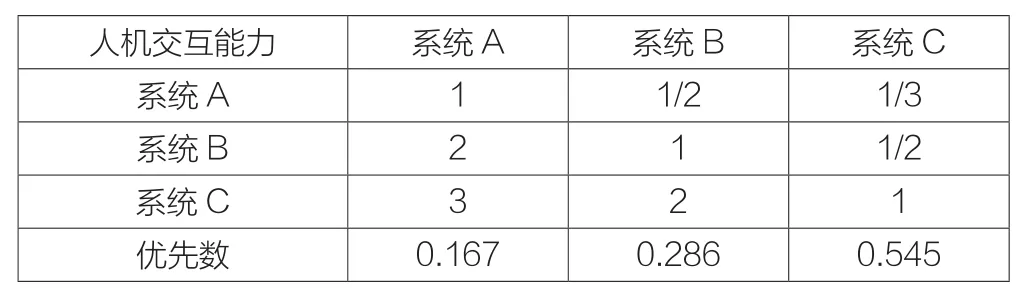
表6 方案层“人机交互能力”判断矩阵和优先数

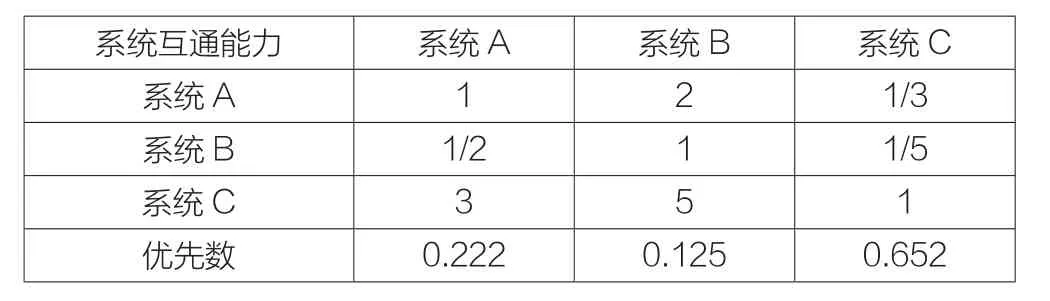
表7 方案层“系统互通能力”判断矩阵和优先数

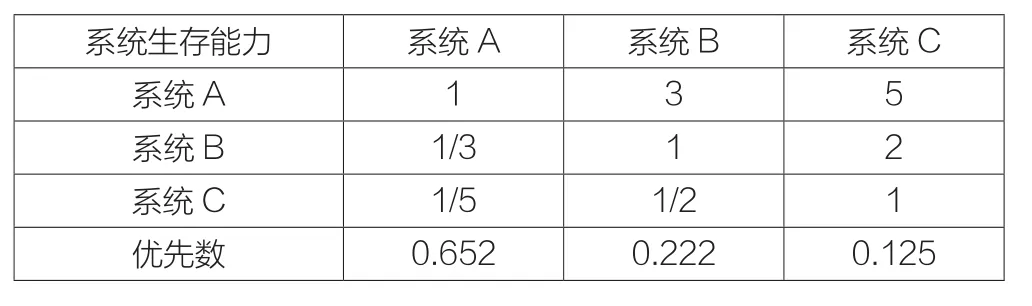
表8 方案层“系统生存能力”判断矩阵和优先数

表9 方案层“系统安全保密能力”判断矩阵和优先数

计算综合优先数，确定排序

为了得到递阶层级结构模型中所有元素相对于总目标的权重，需要适当组合上一步计算结果，以计算出总排序的相对权重。这一步通常是由上而下逐层进行，最终得出方案层的优先顺序。具体步骤是首先将准则层的优先数向量作为该层的组合优先数，然后使用方案层的单排序优先数乘以相应上层元素的优先数并求和，得出方案层的综合优先数，如表10所示。

表10 方案层综合优先数

效能评估结果分析

由上述层次分析法综合优先数的计算结果可知，系统A的作战效能最好，特别是它的情报获取能力、信息传输能力、信息处理能力以及辅助决策能力和系统生存能力都是三个系统中最好的。系统B和系统C作战效能基本相当，系统B在系统安全保密能力上最强，系统C在人机交互能力和系统互通能力上最强。

结语

层次分析法将复杂问题层次化，逐层分析各影响因素，具有定性和定量分析相结合、适用范围广、推广应用价值强等特点。通过实例分析，在指挥信息系统效能评估过程中，该方法具有较强的适用性，评估结果符合实际情况。但是，层次分析法还处于发展过程中，其理论不断丰富，在指挥信息系统效能评估领域还处于探索阶段，在层次结构的合理性、判断矩阵的一致性等方面还有待于进一步完善和提高。

DOI：10.3969/j.issn.1001-8972.2016.06.010