幂律流体中岩屑颗粒沉降速度实验

孙晓峰，纪国栋，冯松林，陈志学，李显义，曲从锋（.中国石油大学（北京）石油与天然气工程博士后科研流动站，北京 000；.中国石油集团钻井工程技术研究院，北京 006；.中国石油长庆油田分公司第六采油厂，陕西 榆林 79000）



幂律流体中岩屑颗粒沉降速度实验

孙晓峰1，纪国栋2，冯松林3，陈志学2，李显义2，曲从锋2
（1.中国石油大学（北京）石油与天然气工程博士后科研流动站，北京 102200；2.中国石油集团钻井工程技术研究院，北京 102206；3.中国石油长庆油田分公司第六采油厂，陕西 榆林 719000）

钻井过程中，任何井型都需要钻井液有效携带岩屑上返，以保持井眼清洁；但由于岩屑颗粒与钻井液存在密度差，遇到接单根、停钻等工况，岩屑颗粒就会在钻井液中沉降。对于大斜度井和水平井，岩屑沉降后会堆积在造斜和水平井段，形成岩屑床，造成恶性井下安全事故，因此，深入研究岩屑颗粒在钻井液中的沉降规律十分重要。文中首先综述了不同形状、不同粒径的固体颗粒在牛顿流体中的阻力系数和沉降速度计算模型，分析了牛顿流体中固体颗粒雷诺数和阻力系数之间的关系；应用与研究固体颗粒在牛顿流体中沉降的相同方法，并通过室内实验，得到了不同粒径岩屑颗粒在幂律流体中的沉降速度模型、颗粒雷诺数与阻力系数之间的关系模型。

岩屑颗粒；沉降；幂律流体；阻力系数；沉降速度

0　引言

油气钻井过程中产生的岩屑的运动轨迹与井型有关。进行水平井钻进时，岩屑分别沿水平段、造斜段和直井段上返运移至井口［1-2］；进行定向井钻进时，岩屑沿造斜段和直井段最终运移至井口；而打直井时岩屑仅沿直井段上返运移：即无论哪种井型岩屑最终均存在直井段岩屑上返运移。因此，深入研究岩屑在钻井液中的沉降规律十分必要。在接单根、设备检修等停钻工况下，岩屑颗粒在钻井液中会自由沉降，沉降速度大小关系到直井段的岩屑浓度变化，同时影响造斜段岩屑沉积厚度。如岩屑颗粒沉降速度快，会在造斜段迅速形成岩屑床，存在岩屑床崩塌埋井眼的潜在风险。深入研究岩屑颗粒在钻井液中的沉降规律，是准确计算岩屑床沉积厚度、预测岩屑床崩塌风险的理论基础。

在对液体中固体颗粒的沉降规律研究方面，1850 年G.G.Stokes［3］即推导出了球体岩屑颗粒在液体中自由沉降的阻力公式，钱宁［4］1981年通过水中的泥沙自由沉降实验得出了不同颗粒雷诺数范围的阻力系数公式，William［5］，Turton［6］，Ibad-zade［7］，Brown［8］等学者分别于1982年、1987年、1992年和2003年通过实验研究了石英砂、天然泥沙在水中的沉降规律。但以上学者多以泥沙、球体岩屑颗粒在水介质中沉降进行研究，而钻井过程中，循环介质是钻井液，通常为幂律流体，故本文研究中引入表征岩屑形状和粗糙度的相关参数，并通过室内实验来研究岩屑颗粒在幂律流体中的沉降阻力系数与沉降末速度问题。

1　牛顿流体中岩屑颗粒的沉降末速度

钻井过程中产生的岩屑颗粒因与钻井液存在密度差，会出现滑脱沉降现象。假设直径为d的球形岩屑颗粒在液体（牛顿流体）中作沉降运动，沉降过程中受到重力、浮力的作用，合力即浮重（FB）：

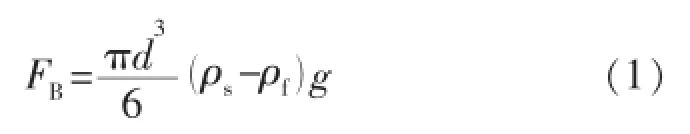
式中：d为球体岩屑颗粒直径，m；g为重力加速度，N/ kg；ρs，ρf分别为球体岩屑颗粒和流体的密度，kg/m3。

由于液体黏性和球体岩屑颗粒运动的惯性，球形岩屑颗粒表面受到液体黏性阻力和压差阻力的作用（见图1），将压差阻力与形状阻力合并，总阻力FD为

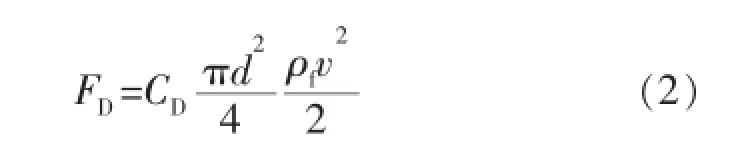
式中：v为球体岩屑颗粒的运动速度，m/s；CD为总阻力系数（简称阻力系数）。

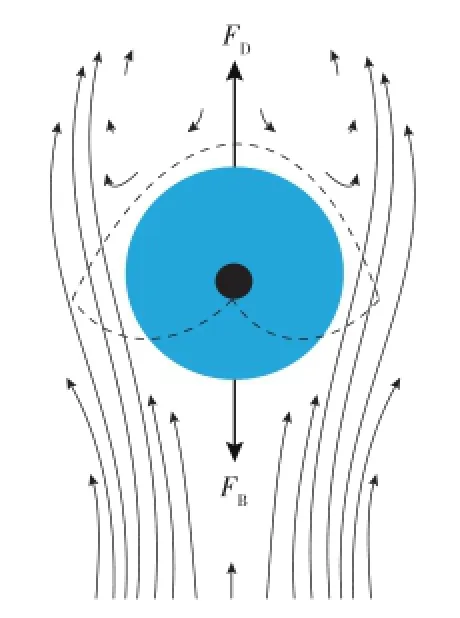
图1　球体岩屑颗粒受力示意

当球体岩屑颗粒浮重与总阻力达到平衡（即FB= FD）时，球体岩屑颗粒开始作匀速沉降运动，达到沉降末速度。此时，有受力平衡方程：

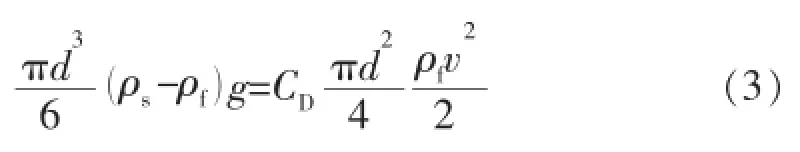
整理得沉降末速度表达式：

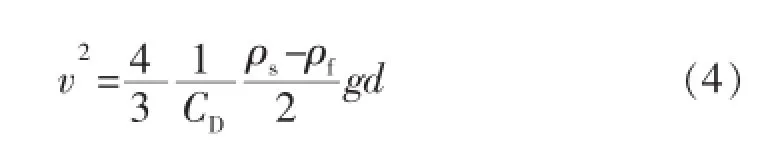
由式（4）可知，求解球体岩屑颗粒沉降末速度，核心问题是求解阻力系数CD，而CD是雷诺数的函数。当球体岩屑颗粒在液体中沉降时，颗粒沉降速度即为液体相对速度，球体岩屑颗粒直径即为液流运动的当量直径。颗粒雷诺数Rep为

式中：μ为液体动力黏度，Pa·s。

当液体为幂律流体时，采用Chhabra［9］的黏度表达公式：

式中：K为稠度系数，Pa·sn；n为流型指数。

Stokes推导的球体岩屑颗粒在液体中自由沉降的阻力公式，即斯托克斯定律为

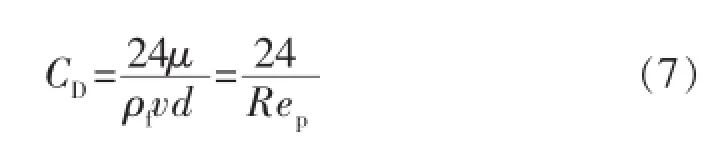
一般认为，斯托克斯定律适用范围为Rep＜1。

2　牛顿流体中岩屑颗粒的阻力系数

钻井过程中产生的岩屑与假设的球体岩屑颗粒岩屑的区别是表面尖锐且不规则。根据钻井液物性、岩屑的最大粒径等参数，可以确定钻井液中岩屑颗粒雷诺数的极限范围在0～500，即在层流和过渡流范围内。描述岩屑颗粒形状特征可用三轴径方法，测得岩屑颗粒的3个正交方向的直径，则岩屑当量粒径dp可表示为

式中：a为岩屑颗粒的长轴直径，m；b，c分别为2个与长轴正交的直径，m。

由于形状对岩屑在钻井液中的运动有很大影响，岩屑形状的不规则程度可由Corey［10］1949年定义的形状系数Sf表示，其表达式为

N.S.Cheng［11］1997年给出了适用于牛顿流体的通用阻力系数关系式：

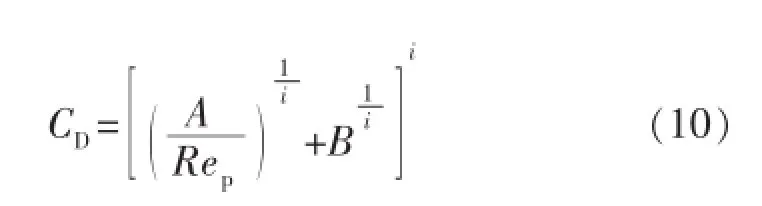
式中：A，B为常数；i为待定幂指数。

N.S.Cheng研究了 William，Turton，Ibad-zade，Brown等学者关于天然泥沙在水中沉降的实验数据，回归得到的所建立模型中幂指数i的平均值为1.50，A取值32.0，B取值1.0，得到的阻力系数公式为

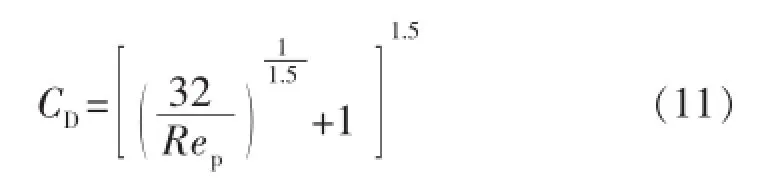
其他学者的实验数据回归出的A，B，i值见表1。

表1　其他学者实验数据回归的A，B，i值

G.Williams［15］1966年定义了固体颗粒表面粗糙度系数P。该系数取值介于0～6：对于尖锐、有棱角的颗粒，取P=0；完全光滑的颗粒，取P=6；压碎的岩石颗粒，取P=2。

B.Camenen［16］根据W.Dietrich［17］的实验数据回归得出了包括形状系数和粗糙度系数的阻力系数表达式：

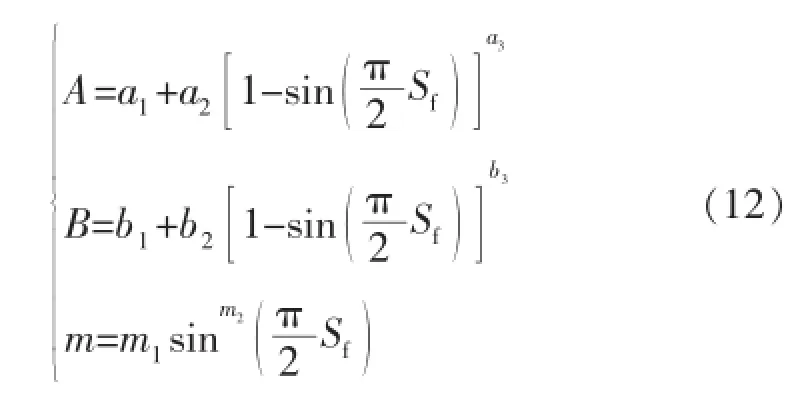
其中：a1=24，b1=0.39+0.226-P，m1=1.2+0.12P；a2= 100，b2=20，m2=0.47；a3=2.1+0.06P，b3=1.75+0.35P。

B.Camenen根据式（12）确定的系数值见表2。

表2　B.Camenen根据式（12）确定的系数值

根据表2中推荐的系数，B.Camenen得出的在牛顿流体中的岩屑沉降阻力系数为

3　幂律流体中岩屑颗粒沉降实验

B.Camenen的模型给出了包含天然泥沙、破碎岩屑的形状系数和粗糙度系数的阻力系数方程，但仅适用于牛顿流体。钻井液流变性一般符合幂律模型，为了解岩屑在钻井液中的沉降规律，以下在借鉴研究岩屑在牛顿流体中沉降规律方法的同时，通过室内实验，研究不同粒径岩屑在幂律流体中的沉降规律。

3.1岩屑颗粒的分选制备

选择了沉积岩岩屑和碳酸盐岩岩屑开展沉降实验，使用9组不同网径的筛网筛分岩屑颗粒（见表3）。

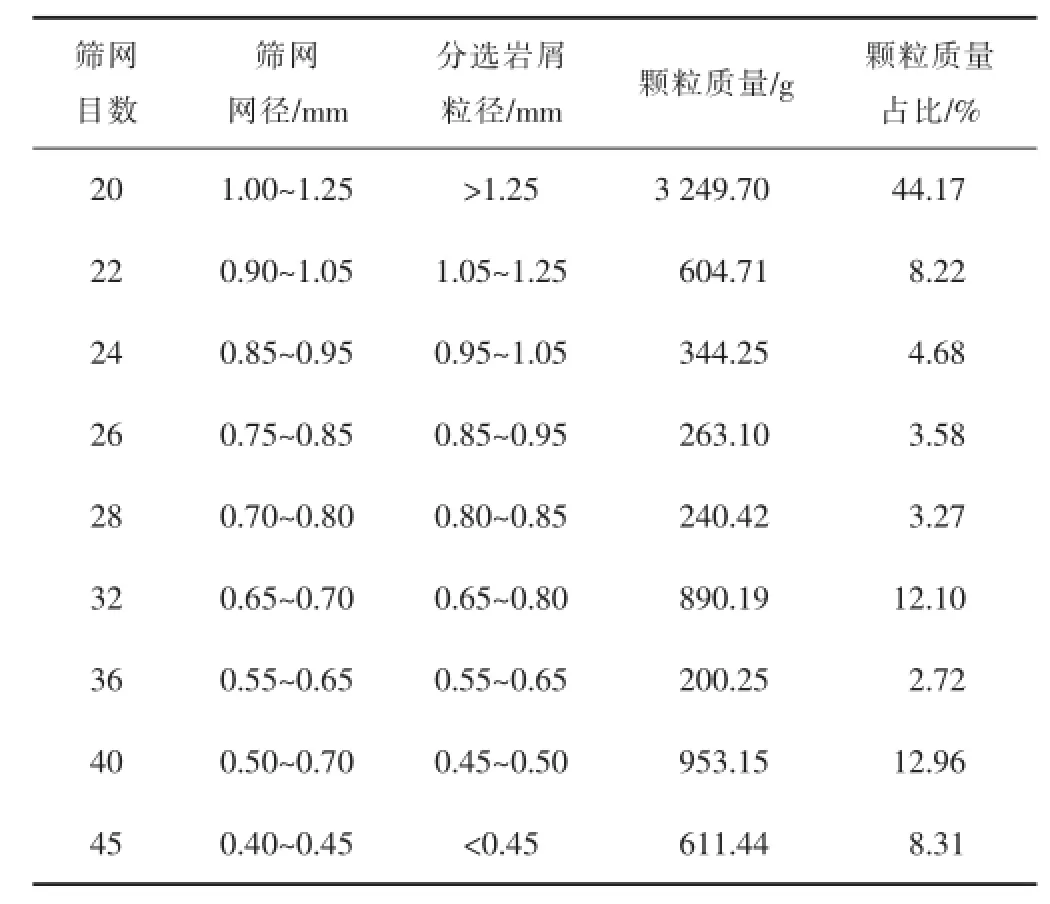
表3　岩屑颗粒分选情况

3.2实验流体制备和实验装置

选用符合幂律模型的PAM（聚丙烯酰胺聚合物）溶液代替现场钻井液。实验制备了4种质量浓度分别为320，550，700，800 mg/L的PAM溶液。沉降实验使用直径100 mm、长度1.7 m的有机玻璃管。

3.3PAM溶液的流变参数

为了确定所配PAM溶液的流变性质，应用流变仪测量了4种PAM溶液在25 C°下的流变参数。测得流变曲线表明，PAM溶液符合幂律模型。4种不同质量浓度的PAM溶液的流变参数见表4。

表4PAM溶液流变参数

3.4岩屑沉降实验结果与分析

对同一粒径范围内的岩屑沉降重复测量25～30次，沉降时间取算数平均值，计算出岩屑沉降末速度，对不同质量浓度的PAM溶液中的沉降实验重复上述步骤并记录数据。

3.4.1颗粒沉降阻力系数

根据颗粒沉降实验结果，绘制了不同粒径范围的CD-Rep曲线（见图2）。

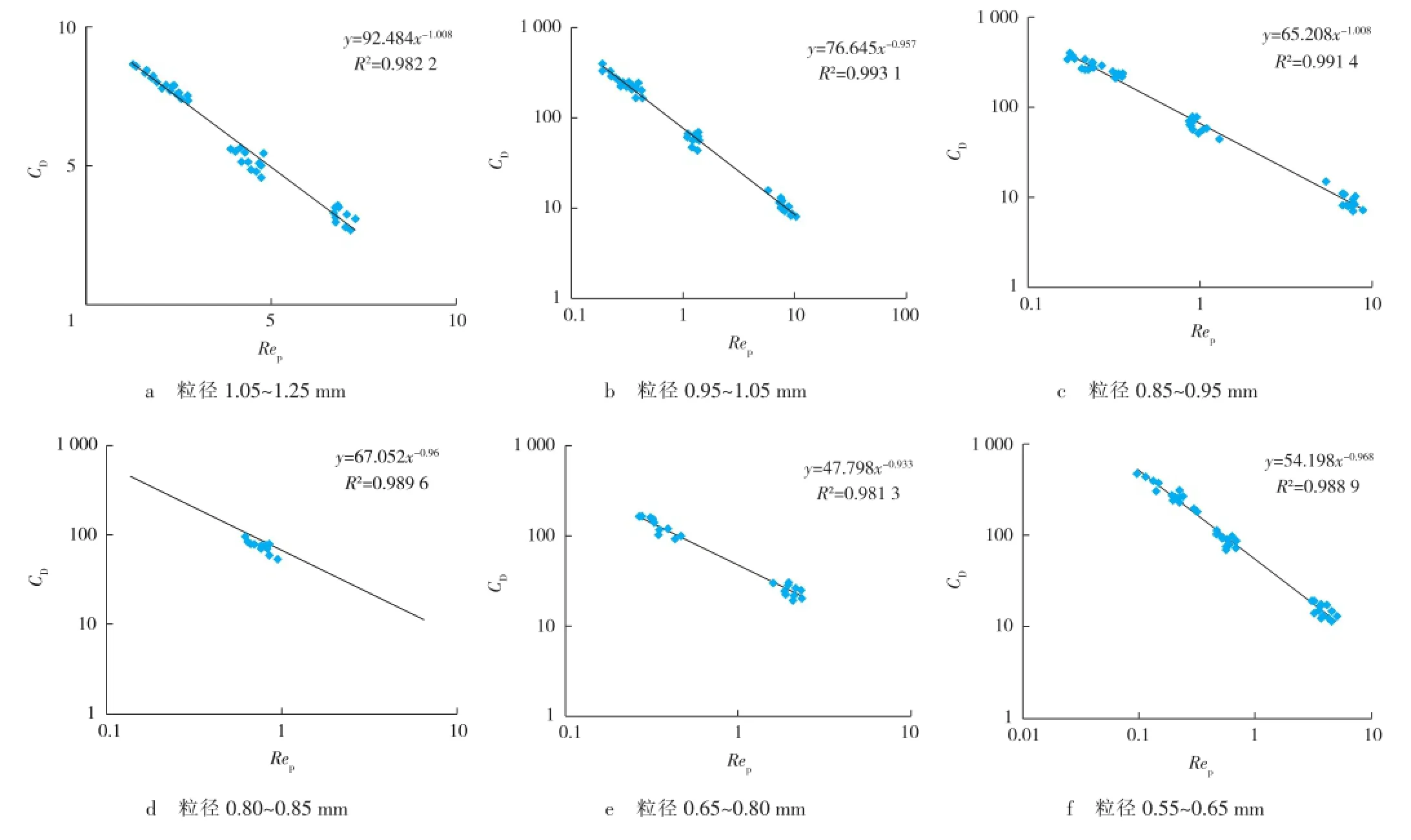
图2　岩石颗粒CD-Rep曲线

根据实验结果，建立了适用于幂律流体中岩屑沉降速度（vp）方程：

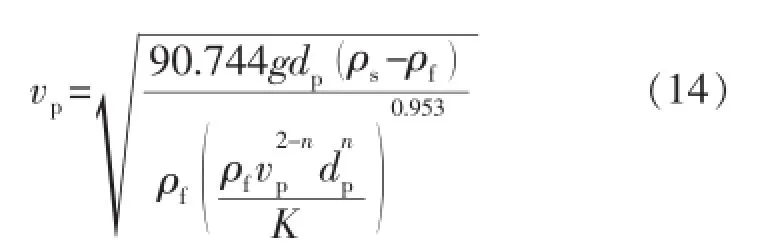
如图3所示，该沉降模型预测结果与实验结果的误差控制在±20%以内。

图3　预测和实验测量阻力系数对比

3.4.2岩屑颗粒直径对沉降速度的影响

如图4所示，岩屑颗粒粒径越大，作用在岩屑颗粒上的阻力越小，沉降速度越大，这与Ezekiel［18］的实验结果基本一致。但是，由于部分小粒径颗粒在黏性阻力和浮重的作用下产生聚集，使其沉降速度变大，同时，岩屑颗粒沉降距离越长，颗粒更容易受这些力的影响，影响沉降速度，导致阻力系数增加。

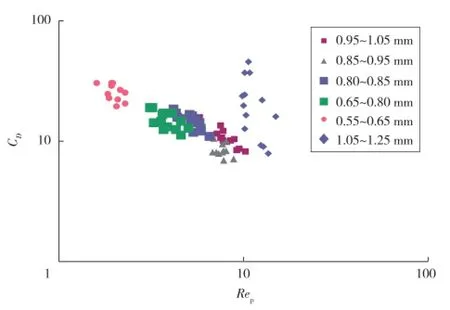
图4　不同粒径范围内的阻力系数变化规律

3.4.3流变性质对岩屑沉降速度的影响

如图5所示，随着PAM溶液质量浓度（稠度系数）的增加，颗粒阻力系数随之增大，其沉降速度随之减小。Zhou［19］的实验也指出，高密度流体会增加颗粒的阻力系数，减小颗粒的雷诺数，使颗粒沉降速度变小。

图5　不同PAM溶液质量浓度下的阻力系数变化规律

4　结束语

钻井过程中，无论任何井型，钻井液有效携带岩屑，保持井眼清洁，都十分重要。钻井液是典型的幂律流体，通过幂律流体中岩屑颗粒沉降室内实验，回归出了不同粒径范围内岩屑颗粒的阻力系数与颗粒雷诺数之间的关系模型，模型预测精度在±20%以内。该模型可为预测岩屑床形成速度及其下滑风险提供理论指导，满足油气钻井的工程需要。

［1］ 李皋，肖贵林，李小林，等.气体钻水平井岩屑运移数值模拟研究［J］.石油钻探技术，2015，43（4）：66-72.

［2］ 宋先知，李根生，王梦抒，等.连续油管钻水平井岩屑运移规律数值模拟［J］.石油钻探技术，2014，42（2）：28-32.

［3］Stokes G G.On the effect of the internal friction of fluids on the motion of pendulums［J］.Transactions of the Cambridge Philosophical Society，1850，9（2）：38.

［4］钱宁，万兆惠.泥沙运动学［M］.北京：科学出版社，2003：45-50.

［5］William E，Dietrich.Settling velocity of natural particles［J］.Water Resources Research，1982，18（6）：1615-1626.

［6］Turton R，Clark N N.An explicit relationship to predict spherical particleterminalvelocity［J］.PowerTechnology，1987，53（2）：127-129.

［7］Ibad-zade Y A.Movement of sediment in open channels［J］. Hydrotechnical Construction，1975，9（5）：498-499.

［8］Brown，P P，Lawler D F.Sphere drag and settling velocity revisited ［J］.Journal of Environmental Engineering，2003，129（3）：222-231.

［9］Chhabra R P.Motion of spheres in power law（viscoinelastic）fluids at intermediate Reynolds numbers：A unified approach［J］.Chemical Engineering&Processing，1990，28（90）：89-94.

［10］Corey A.Influence of the shape on the fall velocity of sand grains［D］. Fort Collins：Colorado A&M College，1949.

［11］Cheng，N S.Simplified settling velocity formula for sediment particle ［J］.Journal of Hydraulic Engineering，1997，123（2）：149-152.

［12］Dallavalle J.Micrometrics：The technology of fine particles［M］. London：Pitman Publishing Ltd，1948.

［13］Julien P.Erosion and sedimentation.Cambridge［M］.Cambridge：Cambridge University Press，1995.

［14］SoulsbyR.Dynamicsofmarinesands，amanualforpracticalapplications ［M］.London：Thomas Telford，1997.

［15］Williams G.Particle roundness and surface texture effects on fall velocity［J］.Journal of Sedimentary Petrology，1966，36（1）：255-259.

［16］Camenen B.Simple and general formula for the settling velocity of particles［J］.Journal of Hydraulic Engineering，2007，133（2）：229-233.

［17］Dietrich W.Settling velocities of natural particles［J］.Water Resource Research，1982，18（6）：1615-1626.

［18］Ezekiel E E.Experimental study of drilling mud rheology and its effect on cuttings transport［D］.Trondheim：Norwegian University of Science and Technology，2012.

［19］Zhou L.Hole cleaning during underbalanced drilling in horizontal and inclinedwellbore［J］.SpeDrilling&Completion，2008，23（3）：267-273.

（编辑李宗华）

Cuttings particle settling velocity within power law fluid

Sun Xiaofeng1，Ji Guodong2，Feng Songlin3，Chen Zhixue2，Li Xianyi2，Qu Congfeng2
（1.Post-Doctoral Research Center of Oil and Gas Engineering，China University of Petroleum，Beijing 102200，China；2.CNPC Drilling Research Institute，Beijing 102206，China；3.No.6 Oil Production Plant，Changqing Oilfield Company，PetroChina，Yulin 719000，China）

Cuttings transport efficiency ought to be ensured for purpose of hole cleaning during the drilling operation for every well type.However，due to the density difference between cuttings particle and drilling fluid，cuttings particles will settle down in drilling fluid in operational mode of pipe connection or overhaul.For large deviation wells and horizontal wells，settling cuttings particles，which accumulate on the surface of direction interval or horizontal interval，will form cuttings bed that causes incident.Thus，a further study on the mechanism of cuttings particle settlement in drilling fluid is very important.In this research，several sorts of calculation model of for drag coefficient and settling velocity within Neotonian fluid，for cuttings particles of different shape or size，are reviewed first.Then，correlation between drag coefficient and particle Reynolds number within Neotonian fluid is analyzed.Thus，using the same research method by which cuttings particle settlement in Newtonian fluid is researched；calculation model for settling velocity of particles of different size and relation model for drag coefficient and particle Reynolds number are obtained.

cuttings particles；settlement；power law fluid；drag coefficient；settling velocity

国家科技重大专项课题“复杂结构井优化设计与控制关键技术”（2011ZX05009-005）；中国石油天然气集团公司科学研究与技术开发项目“水平井减阻降扭与管外封隔器等新工具研制”（2014B-4314）

TE254+.1

A

10.6056/dkyqt201601027

2015-07-24；改回日期：2015-11-20。

孙晓峰，男，1981年生，讲师，博士，研究方向为油气井流体力学与应用。E-mail：suneye@126.com。

引用格式：孙晓峰，纪国栋，陈志峰，等.幂律流体中岩屑颗粒沉降速度实验［J］.断块油气田，2016，23（1）：120-124.

Sun Xiaofeng，Ji Guodong，Chen Zhifeng，et al.Cuttings particle settling velocity within power law fluid［J］.Fault-Block Oil&Gas Field，2016，23（1）：120-124.