井筒压降对底水油藏水平井生产动态的影响

王海静，薛世峰，仝兴华，闫文文（.中国石油大学（华东）储运与建筑工程学院，山东 青岛 66580；.山东大学（威海）机电与信息工程学院，山东 威海 6409；.中国石化胜利油田分公司石油工程技术研究院，山东 东营 57000）



井筒压降对底水油藏水平井生产动态的影响

王海静1，薛世峰1，仝兴华2，闫文文3
（1.中国石油大学（华东）储运与建筑工程学院，山东 青岛 266580；2.山东大学（威海）机电与信息工程学院，山东 威海 264209；3.中国石化胜利油田分公司石油工程技术研究院，山东 东营 257000）

底水油藏水平井生产动态预测是制定油藏开发方案的重要依据。文中将井筒、油藏视为耦合系统，建立了油水两相管流-渗流耦合数学模型和有限元数值模拟方法，在此基础上开展了底水油藏水平井生产动态研究，分析了井筒压降对水平井见水时间、无水采收率及储层动用均衡性的影响。结果表明：井筒压降导致水平井跟端见水时间提前，无水采收率降低，储层动用程度均衡性变差；采液速率越高，井段越长，忽视井筒压降所引起的底水油藏水平井生产动态预测结果的误差则越大。该研究成果对水平井控水方案设计具有一定的参考价值。

底水油藏；水平井；井筒压降；无水采收率；动用均衡性

0　引言

水平井是底水油藏开发的一项重要举措。底水不均匀脊进是制约水平井开发效果的主要因素，将导致油井过早见水和储层动用不均衡。近年来，国内外学者在底水油藏水平井生产动态预测方面做了大量的研究工作。Wibowo等［1］、王家禄等［2］、刘欣颖等［3］通过物理模拟实验分别对均质和非均质底水油藏水脊的形成与发展机理进行了研究；Recham等［4］、周代余等［5］、王敬等［6］通过数值模拟分析了水平井水淹动态特征及其影响因素；程林松等［7］、Al-Enezi等［8］、Permadi等［9］、Karami等［10］基于简化的物理模型分别提出了半解析的水平井临界产量预测模型、见水时间预测模型和见水后生产动态预测模型；曹立迎等［11］根据数值模拟结果拟合出了底水油藏水平井水淹规律的经验模型。生产过程中，井筒与油藏互为边界条件，相互影响，相互制约，构成了一个复杂的井筒-油藏耦合系统。然而上述研究均将井筒视为无限导流，未考虑井筒压降对底水脊进规律和水平井生产动态的影响。鉴于此，李立峰等［12］、郑强等［13］建立了半解析的井筒-油藏耦合模型，分别研究了井筒压降和渗透率非均质性对底水油藏水平井见水时间及含水率变化规律的影响。目前，关于井筒压降对底水油藏水平井生产动态的影响仍缺乏系统深入的研究。本文拟基于油水两相管流-渗流耦合模型，采用数值模拟方法，开展底水油藏水平井生产动态研究，分析井筒压降对底水油藏水平井见水时间、无水采收率及动用均衡性的影响，为底水油藏水平井开发方案的制定、调整，以及完井、堵水工艺措施的选择提供理论指导。

引用格式：王海静，薛世峰，仝兴华，等.井筒压降对底水油藏水平井生产动态的影响［J］.断块油气田，2016，23（1）：73-76.

Wang Haijing，Xue Shifeng，Tong Xinghua，et al.Impacts of wellbore pressure drop on production performance of horizontal wells in bottomwater reservoirs［J］.Fault-Block Oil&Gas Field，2016，23（1）：73-76.

1　数学模型的建立

水平井开采过程中，油藏物理现象复杂、影响因素众多。本文在建立数学模型时，从物理现象的本质出发，提取主要因素，忽略次要因素，作以下基本假设：1）油藏均质、各向同性；2）油、水不混溶，渗流遵循Darcy定律；3）地层岩石与流体均不可压缩；4）整个开采过程恒温；5）不考虑油藏岩石与流体的物理吸附及化学作用。

1.1油藏渗流模型

根据多孔介质渗流的连续性方程和Darcy定律，可建立油水两相渗流模型。

油相：

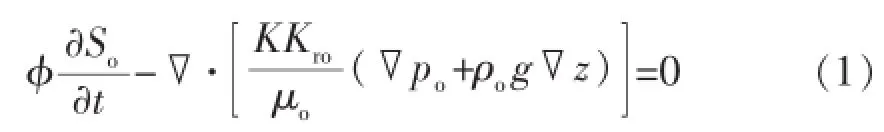
水相：

式中：φ为孔隙度；So，Sw分别为油相、水相饱和度；po，pw分别为油相、水相压力，Pa；K，Kro，Krw分别为绝对渗透率、油相相对渗透率、水相相对渗透率，m2；μo，μw分别为油相、水相黏度，Pa·s；g为重力加速度，N/kg；z为液柱高度，m；ρo，ρw分别为油相、水相密度，kg/m3。

1.2井筒管流模型

水平井开采过程中，井筒流动为变质量流，除管壁摩擦压力损失外，还存在加速压力损失。此外，流体径向流入引起的井筒内壁边界层扰动对沿程压力损失的影响也不可忽视。如将上述因素全部考虑在内，可建立井筒管流模型：

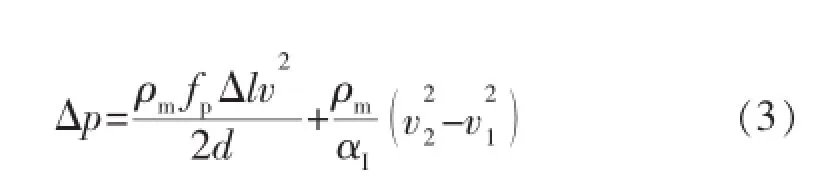
式中：Δp为井筒单元压降，Pa；ρm为混合液平均密度，kg/m3；Δl为井筒单元长度，m；fp为径向流入条件下的井壁摩擦因数［14］；v为井筒截面平均流速，m/s；d为井筒内径，m；αI为动量修正系数［15］；v1，v2分别为井筒单元上、下游的截面平均流速，m/s。

2　数值计算方法的建立

鉴于有限元方法在边界处理以及网格划分等方面的灵活性，本文采用有限元法进行管流-渗流耦合条件下油水两相渗流模型的数值求解。

2.1油水两相渗流

油水两相渗流模型数值求解的关键在于如何避免油水界面处由毛细管力（pc）对水相饱和度导数项的剧烈变化引起的饱和度锋面数值振荡现象。常规的数值解法以油相压力和水相饱和度为求解变量，采用迎风格式计算渗流相关参数，这无疑增加了代码计算量。为此，本文以毛细管力和油相压力作为求解变量，实现了油水界面处毛细管力的自然连续，避免了迎风技术处理数值振荡问题引起的额外计算量，有效地提高了计算效率。以pc和po为求解变量的渗流方程为

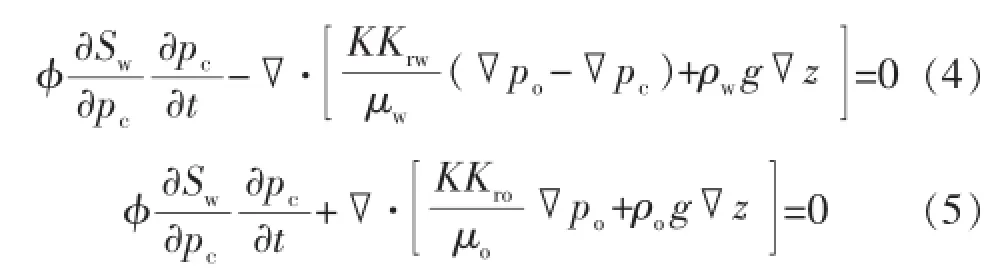
2.2管流-渗流耦合

为实现管流与渗流的耦合，需要在满足交界面流量和压力连续的条件下，同时求解油藏渗流模型和井筒管流模型。然而，由于井筒管流模型的强非线性以及交界面形状的特殊性，常规的联立求解或迭代求解方法在计算效率和收敛性方面并不理想。为此，本文采用等效渗流法实现井筒管流与油藏渗流的耦合，即将井筒管流视为具有一定渗透率的多孔介质渗流。由于管流与渗流在数学模型上实现了统一，交界面流量、压力自然连续，耦合求解的复杂性自然降低。将式 （3）与Darcy定律类比，即可得到井筒的等效渗透率（Ke）计算公式：

由式（6）可以看出，在管壁径向流入的条件下，管道等效渗透率与其截面平均速度有关。而在井筒-油藏耦合系统中，井筒截面速度本身又取决于油藏和井筒的水力传导特性。因此，井筒等效渗透率与截面平均流速之间互为因果，无法通过直接计算得到，必须采用迭代方法求解。Ke初值的选取对迭代法的收敛速率至关重要。本文借鉴层流条件下的井筒压降计算公式，将初始等效渗透率取为d2/37.5。

3　井筒压降对生产动态影响的模拟分析

考虑一底水油藏，地层有效厚度为30 m，面积为400 m×100 m；油藏孔隙度为0.3，渗透率为1 μm2，初始压力为9.1 MPa，含油饱和度为0.75，束缚水饱和度为0.25；油藏条件下油相黏度为5 mPa·s，油相密度为800 kg/m3，水相黏度为1mPa·s，水相密度为1000 kg/ m3；水平井位于油层中心，长度为400 m，井筒半径为0.1 m，采用内径为121 mm套管射孔完井，避水高度为27 m，采液速率为200 m3/d。相对渗透率和毛细管力分别采用式（7）、式（8）、式（9）计算［16］：

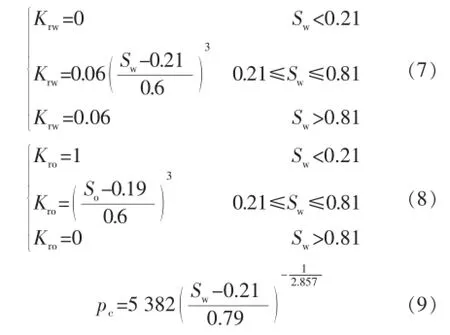
动态模拟结果见图1—图5。从图1可以看出，受井筒压力损失的影响，井筒跟端见水时间比趾端提前约120 d。

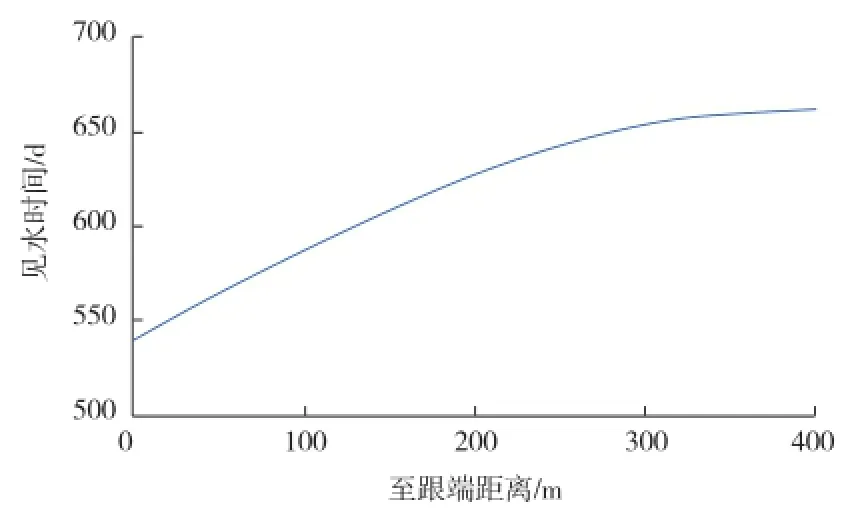
图1　水平井沿程见水时间分布

由图2可以看出：见水前油藏采收率随时间近似线性增大，当生产540 d时，油井见水，此时采收率约为40.5%；见水后，油井含水率迅速上升，油藏采收率的增幅明显减慢，在1 500 d时，含水率达到90%，此时采收率约为58.3%。

由图3可以看出：油井见水前，跟、趾端采收率差值随着时间的延长逐渐增大，当油井见水时达到最大值，约为8.0百分点；跟端见水后，跟、趾端采收率差值开始逐渐减小，但随着整个井段完全见水，跟、趾端采收率差值又进一步增大，当油井含水率为90%时，跟、趾端采收率差值达到6.6百分点。井筒压降对水平井动用均衡性的影响不容忽视。

图2　油藏采收率和油井含水率随时间的变化规律

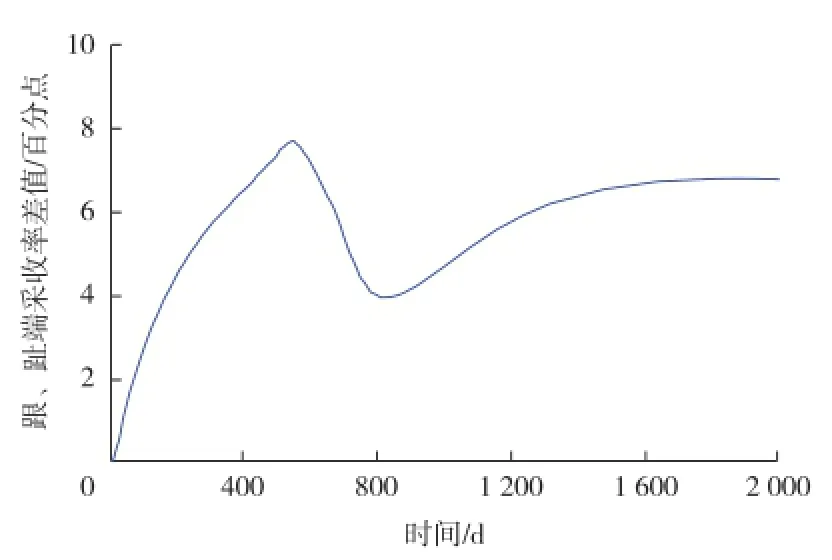
图3　跟、趾端采收率差值随时间的变化规律

由图4可以看出：井筒有限导流（考虑井筒压降）情况下，当采液速率从100 m3/d增大到1 000 m3/d时，见水时间从960 d降到130 d，但无水采收率从40.0%增大到44.0%，二者均与采液速率近似呈对数关系；与有限导流时相比，井筒无限导流（不考虑井筒压降）时见水时间偏长20～50 d，无水采收率偏高2.0～7.0百分点；采液速率越高，无限导流时的无水采收率计算偏差就越大。

由图5可以看出：井筒有限导流情况下，当井段长度从100 m增大到1 000 m时，见水时间从180 d增大到760 d，无水采收率从5.0%增大到23.7%，二者均与井段长度近似呈对数关系；与有限导流时相比，井筒无限导流时见水时间偏长，无水采收率偏高，井段越长，无限导流的计算偏差越大，当井段长度为1 000 m时，无限导流的见水时间偏长500 d，无水采收率偏高14.1百分点，远大于工程设计允许误差。

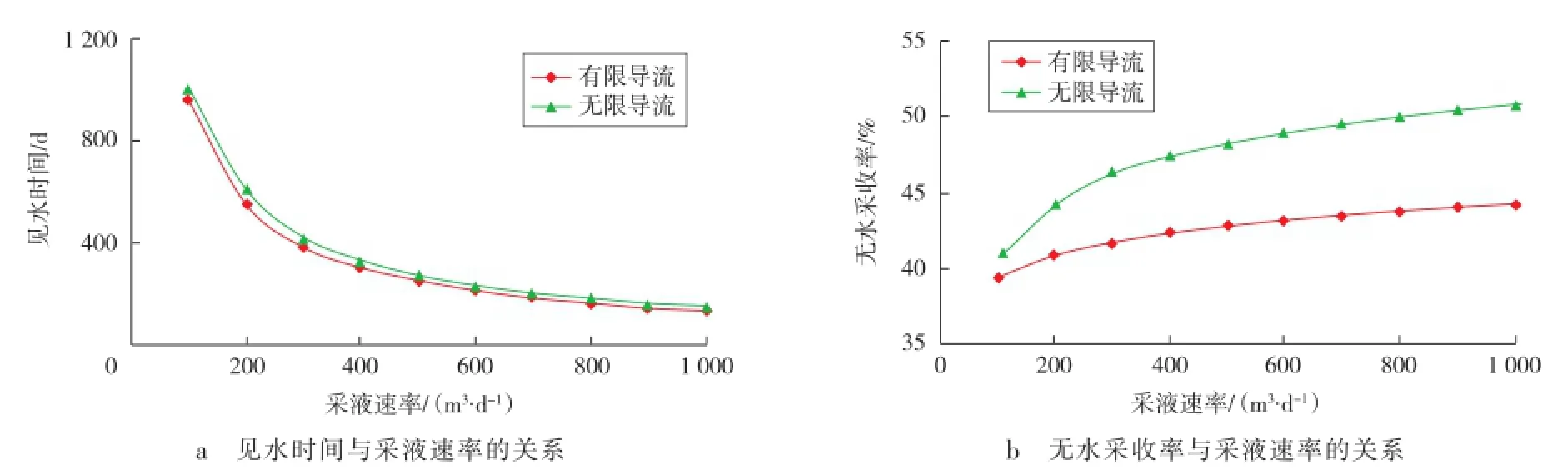
图4　不同采液速率下井筒压降对无水采收率和见水时间的影响

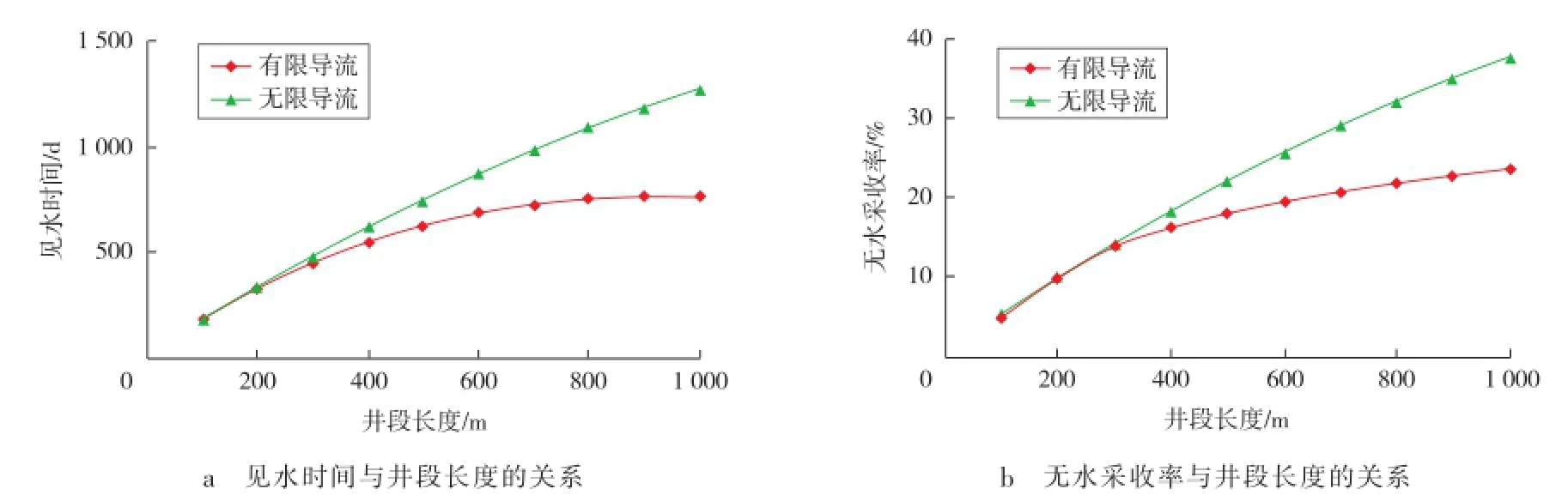
图5　不同井段长度下井筒压降对无水采收率和见水时间的影响

4　结束语

井筒压降导致水平井跟端见水时间提前，无水采收率降低，储层动用程度均衡性变差。忽视井筒压降将导致底水油藏水平井生产动态预测结果产生误差，且采液速率越高、井段越长，误差越大。井筒压降对底水油藏水平井开发效果的影响不可忽视，基于管流-渗流耦合方法，定量分析井筒压降对底水油藏水平井见水时间、无水采收率及动用均衡性的影响，可为底水油藏水平井开发方案的制定、调整和完井、堵水工艺措施的选择提供理论指导。

［1］Wibowo W，Permadi P，Mardisewojo P，et al.Behavior of water cresting and production performance of horizontal well in bottom water drive reservoir：A scaled model study［R］.SPE 87046，2004.

［2］ 王家禄，刘玉章，江如意，等.水平井开采底水油藏水脊脊进规律的物理模拟［J］.石油勘探与开发，2007，35（5）：590-593.

［3］ 刘欣颖，胡平.非均质底水油藏水平井三维物理模拟实验［J］.石油学报，2011，32（6）：1012-1016.

［4］ Recham R，Osisanya S O，Touami M.Effects of water coning on the performance of vertical and horizontal wells：A reservoir simulation study of Hassi R′mel Field，Algeria［R］.SPE 65506，2000.

［5］周代余，江同文，冯积累，等.底水油藏水平井水淹动态和水淹模式研究［J］.石油学报，2004，25（6）：73-77.

［6］王敬，刘慧卿，刘松原，等.非均质底水油藏水平井水淹规律研究［J］.石油学报，2010，31（6）：970-974.

［7］程林松，张健琦，李春兰.底水油藏水平井开发见水后生产动态预测［J］.西南石油学院学报，2002，24（2）：12-14.

［8］Al-Enezi K，Das O P，Aslam M，et al.Water coning model for horizontal wells in high mobility reservoir，West Kuwait［R］.SPE 130302，2010.

［9］Permadi P，Jayadi T.An improved water coning calculation for horizontal wells［R］.SPE 133162，2010.

［10］Karami M，Manshad A K，Ashoori S.The prediction of water breakthrough time and critical rate with a new equation for an Iranian Oilfield［J］.Petroleum Science and Technology，2014，32（2）：211-216.

［11］曹立迎，蔺高敏，宋传真，等.底水油藏水平井水淹规律经验模型［J］.断块油气田，2012，19（3）：323-326.

［12］李立峰，岳湘安，张立娟.考虑井筒压降的底水油藏水平井见水时间研究［J］.西安石油大学学报：自然科学版，2012，27（4）：46-49.

［13］郑强，田冀，李芳，等.非均质底水油藏水平井沿程水淹模型［J］.中国科学：技术科学，2014，44（8）：890-896.

［14］Ouyang L，Arbabi S，Aziz K.General wellbore flow model for horizontal，vertical，and slanted well completions［J］.SPEJ，1998，3 （2）：124-133.

［15］White F M.Fluid mechanics［M］.New York：McGraw-Hill Book Company，1986：339.

［16］薛世峰.非混溶饱和两相渗流与变形孔隙介质耦合作用的理论研究及其在石油开发中的应用［D］.北京：中国地震局地质研究所，2000.

（编辑史晓贞）

Impacts of wellbore pressure drop on production performance of horizontal wells in bottom-water reservoirs

Wang Haijing1，Xue Shifeng1，Tong Xinghua2，Yan Wenwen3
（1.College of Pipeline and Civil Engineering，China University of Petroleum，Qingdao 266580，China；2.School of Mechanical，Electrical&Information Engineering，Shandong University，Weihai 264209，China；3.Research Institute of Petroleum Engineering，Shengli Oilfield Company，SINOPEC，Dongying 257000，China）

Production performance is an important basis for field development project design.Regarding wellbore and reservoir as a coupling system，oil/water two-phase pipe flow-seepage coupling mathematical model and corresponding finite element numerical simulation were established.On this basis，the production performance of horizontal well in bottom-water reservoir was investigated，and the impacts of wellbore pressure drop on water breakthrough time，water-free oil recovery and uniformity of development were analyzed.The results show that wellbore pressure drop can lead to advancement of water breakthrough，low water-free oil recovery and non-uniformity of development.The higher the productivity and the longer the horizontal section is，the greater the prediction error of production performance caused by ignoring wellbore pressure drop is.The result provides a reference for water control design of horizontal well.

bottom-water reservoir；horizontal well；wellbore pressure drop；water-free oil recovery；uniformity of development

国家科技重大专项课题“优化射孔技术研究”（2011ZX05006-002）；中央高校基本科研业务费专项资金资助课题“基于井筒-油藏耦合的热采水平井蒸汽合理配注方法研究”（14CX02104A）；材料强度与结构冲击山西省重点实验室基金资助课题“变形变温条件下管流-渗流耦合数值模拟研究”（14-080100-03）

TE319

A

10.6056/dkyqt201601016

2015-07-28；改回日期：2015-11-14。

王海静，女，1983年生，讲师，主要从事油气田地下工程力学研究。E-mail：lnsywhj@163.com。