基于偏心井反演理论的压裂水平井产能计算方法

何军，范子菲，赵伦，宋珩，李孔绸，吴学林（中国石油勘探开发研究院，北京 100083）



基于偏心井反演理论的压裂水平井产能计算方法

何军，范子菲，赵伦，宋珩，李孔绸，吴学林
（中国石油勘探开发研究院，北京 100083）

基于垂直裂缝稳态渗流等效井径模型、圆形供给边界偏心井反演理论和压降叠加原理，建立了考虑油藏及裂缝渗流的耦合模型，推导了圆形供给边界压裂水平井产能计算新公式，分析了裂缝半长、裂缝条数、裂缝导流能力、裂缝布缝方式对压裂水平井产能的影响。结果表明：压裂水平井裂缝产量是非均匀的，具有边部裂缝产量高，中间裂缝产量低的特点；压裂水平井裂缝存在最优条数，当裂缝条数大于最优条数，水平井产量增加缓慢；裂缝半长增加，水平井产量增加，其中边部裂缝产量增加最显著，中间裂缝产量略有增加；裂缝无因次导流能力增加，水平井产量增加，且很快趋于平稳，在压裂设计中，应避免裂缝导流能力小于曲线的拐点值，引起压裂水平井产能快速下降。最后，通过分析4种布缝方式发现，压裂水平井宜采用交错布缝，同时延长边部裂缝的缝长，适当减小中间裂缝缝长，降低裂缝间的干扰，提高水平井产量。

压裂水平井；等效井径；偏心井反演；压降叠加原理；圆形供给边界

0　引言

压裂水平井技术是实现各种边际油藏有效开发的重要手段，然而压裂水平井的产能计算是渗流力学中的一大难题［1-3］。压裂水平井产能评价方法较多，主要采用保角变换理论、等值渗流阻力法、水电模拟实验、复势理论及数值模拟等方法［4］。郎兆新［5］应用位势理论和叠加原理，得到了压裂水平井产能公式，分析了产量与生产压差、裂缝长度及裂缝条数的关系；范子菲［6］在垂直裂缝稳态解的基础上，利用叠加原理及镜像反演推导出了裂缝性油藏水平井稳态解公式；李廷礼［7］应用复位势理论和叠加原理推导出了考虑地层、裂缝、井筒渗流的稳态产能解；牟宝珍［8］根据水电相似原理，利用等值渗流阻力法建立了考虑启动压力梯度和压敏效应的压裂水平井产能公式；张建军［9］利用保角变换推导出了纵向裂缝内变质量流动时压裂水平气井的产能公式；徐严波等［10-13］将裂缝分成若干微元段，把每个微元段看作点汇，利用叠加原理或积分变换，给出了多裂缝压裂水平井半解析产能模型；吴晓东等［14-15］根据水电相似原理，设计了压裂水平井的电模拟实验，研究了单井状态下和井网条件下裂缝参数对压裂水平井产能的影响；曲占庆等［16-17］分别建立了气藏、油藏压裂水平井渗流模型，对裂缝参数进行了优化设计；张学文等［18-19］利用数值模拟方法研究了压裂水平井的渗流规律，分析了地层及裂缝参数对压裂水平井产能的影响。

以往的压裂水平井模型大多基于无限大地层或矩形边界油藏，而本文应用垂直裂缝等效井径模型，偏心井反演理论和压降叠加原理，建立了考虑油藏及裂缝渗流的耦合模型，推导了圆形供给边界压裂水平井产能预测新公式，并分析了压裂水平井产能影响因素。

1　数学模型的建立

假设：圆形定压边界，地层各向同性，厚度、渗透率为常数；流体为单相不可压缩牛顿流体，黏度为常数，忽略重力、毛细管力的影响；渗流满足达西流动；水平井段只在裂缝与水平井筒相交处射孔，裂缝为有限导流，水平井筒为无限导流；流体由基质进入裂缝，再由裂缝进入水平井井筒；裂缝为矩形裂缝，贯穿整个油藏。

1.1油藏流动模型

压裂水平井裂缝从左至右依次为1，2，3，…，n，裂缝半长为xfi，裂缝宽度为wfi，根据垂直裂缝稳态渗流等效井径模型，裂缝可等效为一口直井（见图1）。

图1　压裂水平井裂缝和定压边界等效图

图1中以3条裂缝为例，根据等效井径模型，3条裂缝可等效为rwe1，rwe2，rwe3的直井，利用偏心井反演理论，得到1，2，3井的共轭井1′，2′，3′，消除边界的作用，此时压裂水平井问题演变为无限大地层多口直井的稳态渗流问题。

由文献［20］可知垂直裂缝等效井径表达式为

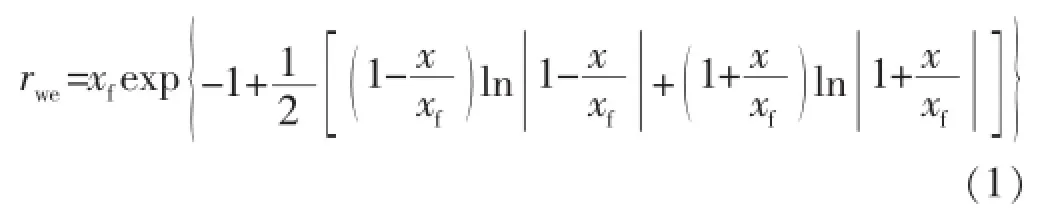
假设裂缝流量均匀，裂缝的等效井径为

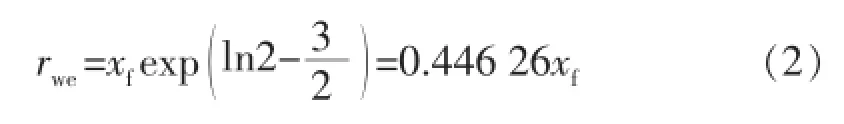
i（1，2，…，n）表示裂缝等效的实际井，i′表示相应的虚拟井，实际井和虚拟井在地层中任意点M产生的势为［21］

由叠加原理，多井同时生产时M点产生的势为

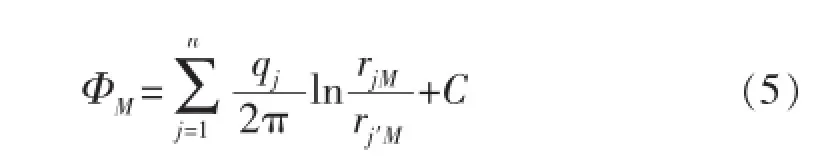
若M点取在供给边界M1（供给边界与x轴的左交点）处，则：

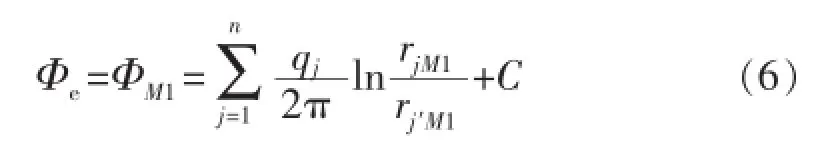
若M点取在等效直井i的井壁处，则：

式（6）减式（7），并将势函数表示成压力的形式得

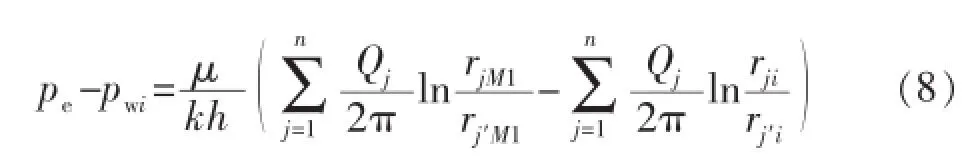
假设裂缝等效井的坐标为（xi，yi），由圆形定压边界偏心井反演理论可以求得虚拟井的坐标（xi′，yi′）。已知实际井、虚拟井、点M1的坐标之后，可求出公式中各点间的距离。

1.2裂缝流动模型

由于裂缝的横截面积远远大于水平井筒横截面积，裂缝内的流体从裂缝边缘向井筒聚集时，如果忽略重力的影响，可以近似看成地层厚度为wfi，流动半径为，边界压力为pfi的平面径向流，故有如下表达式成立：

1.3耦合流动模型

根据耦合关系，油藏流动在裂缝壁面处的压力与裂缝流动在裂缝壁面处的压力相等。由于水平井筒为无限导流，因此井筒中没有压力损失，裂缝流动在水平井筒处的压力与水平井井底流压相等，联立方程式（8）和式（9）得：

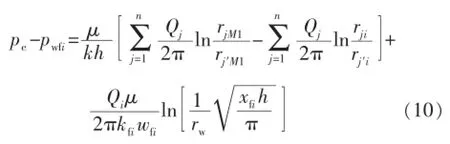
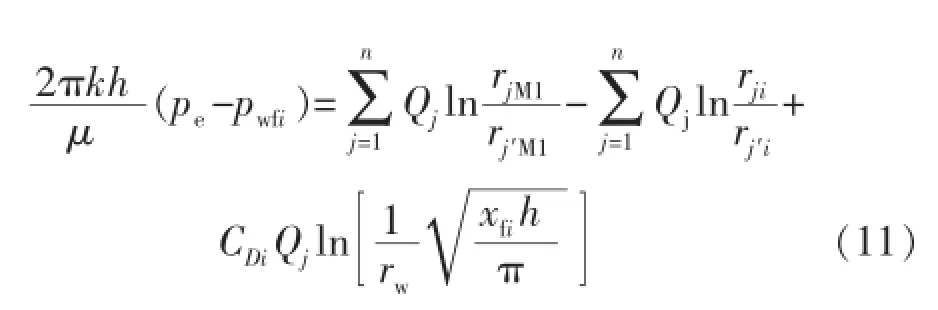
式（11）是第i条裂缝在地层和裂缝中的耦合渗流方程，这样的方程有n个，将其写成矩阵的形式：

式（12）即为压裂水平井所有裂缝渗流时的渗流方程组，公式中的每一项具有明确的物理意义：（A-B）表示流体在地层中的渗流阻力，D表示流体在裂缝中的渗流阻力，Q表示产量，p表示压力，这与等值渗流阻力法是一致的。方程（12）中各矩阵分别为

2　裂缝参数对压裂水平井产能的影响

某油田一口压裂水平井的主要参数：油藏外边界半径500 m，厚度10 m，地层渗透率0.01 μm2，水平井段长800 m，井筒半径0.1 m，原油黏度2 mPa·s，生产压差10 MPa，裂缝宽度5 mm，裂缝渗透率10 μm2。

2.1压裂水平井产量分布

图2为裂缝产量柱状图。

图2　裂缝产量分布

图中5条裂缝半长为100 m。由图可知，裂缝产量呈对称分布，具有两端产量高、中间产量低的特点，裂缝产量不一致是由于裂缝相互干扰所致。

2.2裂缝条数的影响

图3为裂缝条数与压裂水平井产能关系。

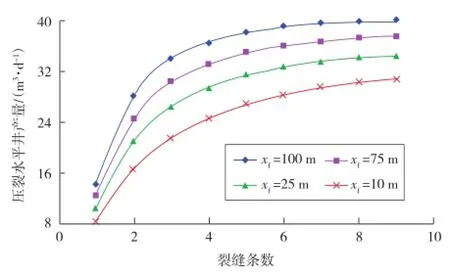
图3　裂缝条数对压裂水平井产能的影响

由图3可以看出，不同裂缝半长下，压裂水平井产量与裂缝条数呈近似对数曲线关系；随着裂缝条数的增加，压裂水平井产量增幅逐渐减小，这是由于裂缝条数增加，缝间干扰加剧。试算结果表明，裂缝半长为100 m时，9条裂缝生产与5条裂缝生产相比，产量增加仅为4.9%。因此，压裂水平井裂缝存在最优条数，当裂缝数量超过它之后，水平井产量增加缓慢。

2.3裂缝半长的影响

图4为裂缝产量与裂缝半长关系。

图4　不同裂缝半长对裂缝产量的影响

由图4可知：不同裂缝半长下，压裂水平井裂缝产量分布曲线。随着裂缝半长的增加，压裂水平井总的产量不断增加，其中，边部裂缝对压裂水平井产量贡献最为明显，中间裂缝产量略有增加。

2.4裂缝无因次导流能力的影响

图5为压裂水平井产量同裂缝无因次导流能力CD关系曲线。当CD≤20时，压裂水平井的产量随CD的增大而急剧增加；当CD＞20时，压裂水平井产量几乎不再增加。因此，在压裂时要注意选择支撑剂类型，避免裂缝闭合过程中，裂缝无因次导流能力小于图中拐点区域，导致水平井产能快速下降。

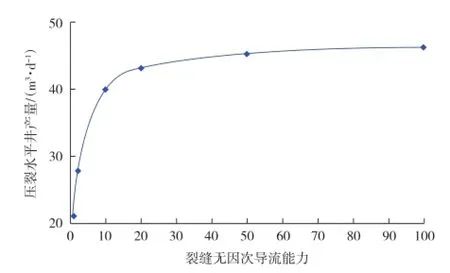
图5　裂缝无因次导流能力对压裂水平井产量的影响

2.5布缝方式的影响

为了研究布缝方式对压裂水平井产量的影响，在水平段长度一定的情况下，设计了4种布缝方式：均匀布缝、哑铃形布缝、交错布缝及边部裂缝加长型布缝，计算了4种布缝方式下压裂水平井产量（见表1）。

表1　不同布缝方式下压裂水平井产量分布

由表1可知：同均匀布缝相比，纺锤形布缝虽然减小了中间裂缝的长度，但水平井总产量几乎不变，产量下降仅为2.2%；交错布缝方式下每条裂缝产量明显提高，水平井总产量增幅最大；边部裂缝加长型布缝方式下，边部裂缝产量增加显著，中间裂缝产量略有降低，水平井总产量增幅较大。综上分析可知，压裂水平井布缝时宜采用交错布缝方式，同时延长边部裂缝的缝长，可适当减小中间裂缝的长度，这样可减小裂缝间的干扰，提高水平井产量。

3　结论

1）对于压裂水平井，裂缝产量不均匀，呈对称分布，且两端裂缝产量较高；随着裂缝条数和裂缝半长的增加，压裂水平井产量增加幅度逐渐变缓；裂缝条数达到一定数值之后，增加裂缝数量对压裂水平井产量提高意义不大。

2）压裂水平井产量随着裂缝无因次导流能力的增加而增加，最后趋于水平。在进行压裂设计时应避免裂缝闭合阶段裂缝导流能力大幅降低，小于曲线拐点，导致压裂水平井产量快速下降。

3）压裂水平井布缝时宜采用交错布缝方式，同时延长边部裂缝的缝长，可适当减小中间裂缝的长度，减小裂缝间的干扰，提高水平井产量。

4　符号注释

h为地层厚度，m；n为裂缝条数；xfi为i裂缝的裂缝半长，m；wfi为i裂缝的裂缝宽度，m；rwei为 i裂缝的等效井径，m；rwe为裂缝等效井径，m；xf为裂缝半长，m；i为i裂缝对应的等效井；i′为i裂缝对应的虚拟井；M为地层中任意一点；ΦiM为i裂缝等效井在M点产生的势，m2/s；qi为单位厚度地层i裂缝产量，m2/s；riM为i裂缝等效井距M点的距离，m；Ci，Ci′，C为常数；Φi′M为i裂缝虚拟井在M点产生的势，m2/s；ri′M为i裂缝虚拟井距M点的距离，m；ΦM为等效井和虚拟井在M点产生的势，m2/s；M1为圆形供给边界与x轴的左交点；ΦM1为等效井和虚拟井在M1点产生的势；m2/s；Φe为供给边界上的势，m2/s；Φwi为i裂缝等效井井壁上的势，m2/s；rji为等效井j距等效井i的距离，m；rj′i为虚拟井j距等效井i的距离，m；pe为外边界压力，Pa；pwi为油藏流动在i裂缝等效井井壁上的压力，Pa；μ为流体黏度，Pa·s；k为地层渗透率，m2；Qj为j裂缝产量，m3/s；xi为等效井i的横坐标；yi为等效井i的纵坐标；Re为油藏半径，m；xi′为虚拟井i的横坐标；yi′为虚拟井i的纵坐标；pfi为裂缝流动中裂缝i的外边界压力，Pa；pwfi为裂缝流动中裂缝i在井筒处的压力，Pa；kfi为i裂缝的渗透率，m2；rw为水平井筒半径，m；pwf为水平井井底流压，Pa；CDi为i裂缝的无因次导流能力；A，B，D，Q，p为压裂水平井渗流方程组系数矩阵。

［1］ 赵文智，胡永乐，罗凯.边际油田开发技术现状、挑战与对策［J］.石油勘探与开发，2006，33（4）：393-398.

［2］ Love T G，McCarty R A，Surjaatmadja J B，et al.Selectively placing many fractures in openhole horizontal wells improves production［J］. SPE 74331-PA，2001，16（4）：219-224.

［3］李宗田.水平井压裂技术现状与展望［J］.石油钻采工艺，2009，31 （6）：13-18.

［4］Penmatcha V R.Modeling of horizontal wells with pressure drop in the well［D］.Palo Alto：Stanford University，1997.

［5］郎兆新，张丽华，程林松.压裂水平井产能研究［J］.石油大学学报：自然科学版，1994，18（2）：43-46.

［6］范子菲，方宏长，牛新年.裂缝性油藏水平井稳态解产能公式研究［J］.石油勘探与开发，1996，23（3）：52-57.

［7］李廷礼，李春兰，吴英，等.低渗透油藏压裂水平井产能计算新方法［J］.中国石油大学学报：自然科学版，2006，30（2）：48-52.

［8］牟珍宝，袁向春，朱筱敏.低渗透油藏压裂水平井产能计算方法［J］.现代地质，2009，23（2）：337-340，346.

［9］张建军，吴晓东，孙天礼.低渗透气藏纵向缝压裂水平气井稳态产能计算方法［J］.天然气工业，2008，28（4）：96-98.

［10］徐严波，齐桃，杨凤波，等.压裂后水平井产能预测新模型［J］.石油学报，2006，27（1）：89-92.

［11］曾凡辉，郭建春，徐严波，等.压裂水平井产能影响因素［J］.石油勘探与开发，2007，34（4）：474-477，482.

［12］汪志明，齐振林，魏建光，等.裂缝参数对压裂水平井入流动态的影响［J］.中国石油大学学报：自然科学版，2010，34（1）：73-78.

［13］Raghavan R，Joshi S D.Productivity of multiple drainholes or fractured horizontal wells［J］.SPE Formation Evaluation，1993，8（1）：1-16.

［14］吴晓东，隋先富，安永生，等.压裂水平井电模拟实验研究［J］.石油学报，2009，30（5）：740-743，748.

［15］曲占庆，曲冠政，何利敏，等.压裂水平井裂缝分布对产能影响的电模拟实验［J］.天然气工业，2013，33（10）：52-58.

［16］曲占庆，黄德胜，李小龙，等.低渗气藏压裂水平井裂缝参数优化研究与应用［J］.断块油气田，2014，21（4）：486-491.

［17］杜现飞，殷桂琴，齐银，等.长庆油田华庆超低渗油藏压裂水平井压裂裂缝优化［J］.断块油气田，2014，21（5）：668-670.

［18］张学文，方宏长，裘怿南，等.低渗透率油藏压裂水平井产能影响因素［J］.石油学报，1999，20（4）：51-55.

［19］任龙，苏玉亮，王文东，等.分段多簇压裂水平井渗流特征及产能分布规律［J］.西安石油大学学报：自然科学版，2013，28（4）：55-59.

［20］于国栋.水平井产能分析理论与方法研究［D］.北京：中国地质大学能源学院，2006.

［21］孔祥言.高等渗流力学［M］.合肥：中国科学技术大学出版社，1999：73-74.

（编辑付丽丽）

Productivity calculation of fractured horizontal well based on equivalent eccentric well inverse theory

He Jun，Fan Zifei，Zhao Lun，Song Heng，Li Kongchou，Wu Xuelin
（Research Institute of Petroleum Exploration&Development，PetroChina，Beijing 100083，China）

Based on equivalent wellbore radius model of vertical fracture in steady state flow，eccentric well inverse theory of circular supply boundary and the principle of pressure-drop superposition，a coupling model of reservoir and fracture flow was developed and a new productivity formula of fractured horizontal well was derived.The influence of fracture half length，fracture numbers，fracture flow conductivity and fracture distributions on the productivity of fractured horizontal well was analyzed.The results show that the distribution of fracture productivity is not uniform with high production in outer fractures and low productivity in inner fractures；there is an optimal fracture numbers，the productivity of horizontal well increases slowly when the fracture numbers exceeds the optimal fracture numbers；with the increase of fracture half length，the productivity of horizontal well increases，the increase of outer fracture productivity is remarkable and the inner fracture productivity rises slightly；with the increase of fracture dimensionless flow conductivity，the productivity of horizontal well increases and tends to be steady quickly；the productivity of horizontal well decreases quickly if the fracture flow conductivity is less than the value of inflection point；finally，analyzing four types of fracture distribution，it is better to adopt interlaced fracture distribution pattern，prolong the length of outer fractures，and reduce the length of inner fractures appropriately to reduce fracture interference and improve the productivity of horizontal well.

fractured horizontal well；equivalent wellbore radius；eccentric well inverse theory；principle of pressure-drop superposition；circular supply boundary

中国石油天然气股份有限公司重大科技专项“哈萨克斯坦碳酸岩盐油气藏气顶和油环协同开发技术研究与应用”（2011E-2504）

TE357.1

A

10.6056/dkyqt201601013

2015-09-28；改回日期：2015-11-11。

何军，男，1987年生，博士研究生，主要从事海外油气田油藏工程研究工作。E-mail：hejun18@126.com。

引用格式：何军，范子菲，赵伦，等.基于偏心井反演理论的压裂水平井产能计算方法［J］.断块油气田，2016，23（1）：60-64.

He Jun，Fan Zifei，Zhao Lun，et al.Productivity calculation of fractured horizontal well based on equivalent eccentric well inverse theory［J］.Fault-Block Oil&Gas Field，2016，23（1）：60-64.