2014年于田MS7.3地震的疑似障碍体效应

刘双庆　陈向军　王熠熙　王俊菲

摘要：利用新疆和田台阵首波Pn段前4s的高频波动形态，分析了2014年于田M_S7.3主震破裂初期几个疑似破裂点的相对位置，给出两种可能的初始破裂点运动学扩展模型。并利用震中距约58km的于田台站数据进一步对该模型进行阐述。分析结果推测：此次于田大地震，其起始破裂点开始于一个水平各向异性较强的点位，在之后的3s内破裂过程向各向异性相对较弱的区域发展，且破裂矢量略向南扩展。

关键词：和田台阵；Pn段；破裂扩展；障碍体

中图分类号：P315.72 文献标识码：A 文章编号：1000-0666（2016）02-0295-08

O 引言

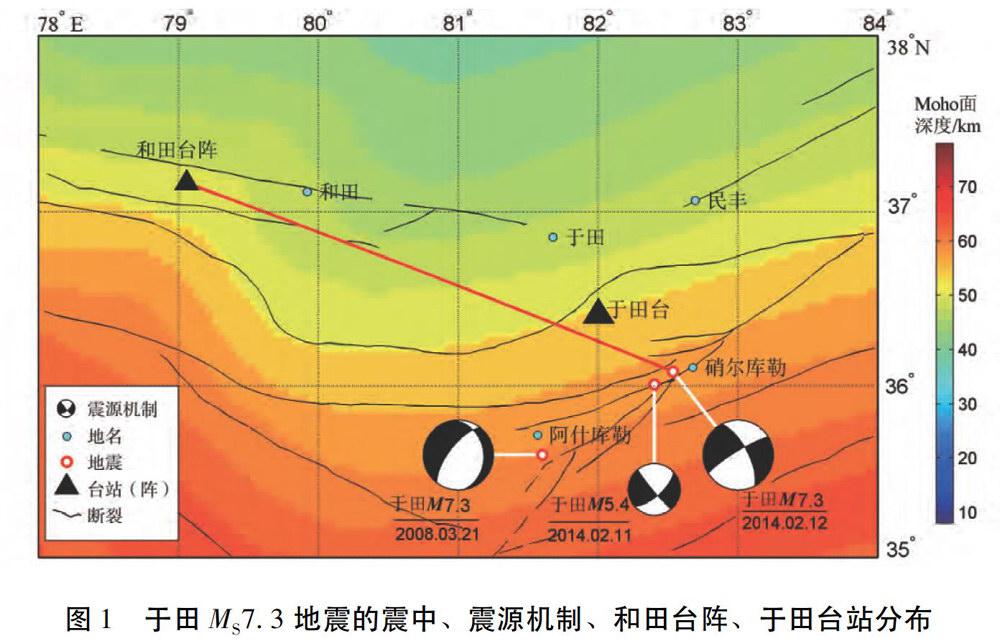
2014年2月12日17时19分48秒，在新疆于田（36.123°N，82.499°E）发生了M_S7.3大地震。这次地震震中位于距2008年3月21日于田M_S7.3地震的北东东向约90km处，在GoogleEarth地图上显示位于硝尔库勒高原湖泊西南角，是阿尔金大断裂的西南缘“爪”状分枝断裂交汇部位。该处北东东向的二级断裂比较发育，如阿龙断裂、库牙克断裂等（国家地震局《阿尔金活动断裂带》课题组，1992；杨万志等，2005）。距离震中北西向约328km处的和田台阵清晰地记录了本次地震的波形，距离震中约58km的于田台记录到清晰的P波段波形（S波段记录限幅）。于田M_S7.3地震发生后，中国地震局监测预报司地震震源深度推进研究小组参加了这次地震的室内资料应急处理工作，并得到一些相关的研究结果（陈向军等，2014；宋秀青等，2014；王俊等，2014），但这些研究都未对台阵记录的初至的一些高频成分展开分析。实际上利用台阵数据分析某些地震破裂过程时，由于其地震射线具有相近的传播路径，更利于反演震源处信息。因此，本文对和田台阵记录波形中的前几秒的高频成分作进一步分析，以期获得于田M_S7.3地震的一些震源运动过程特征。

1 和田台阵入射线方位角分析

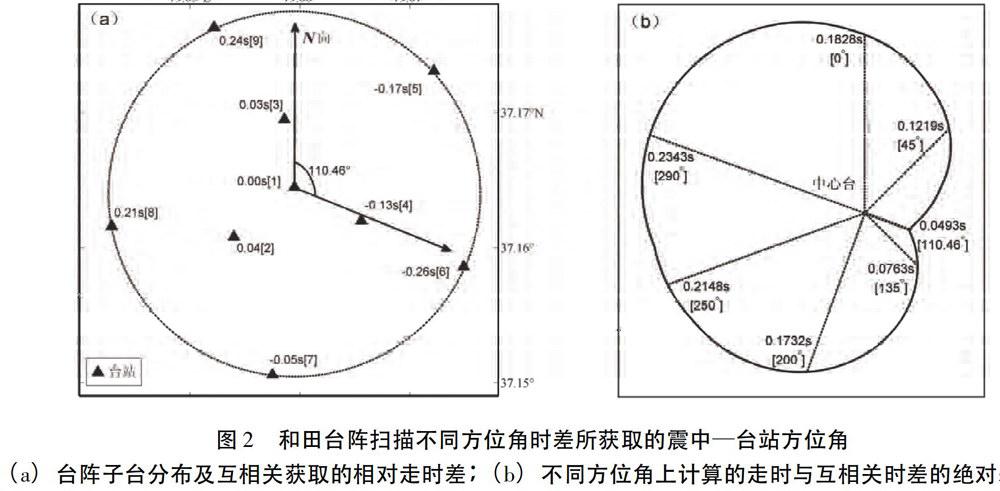
2008、2014年于田两次M_S7.3地震，相关断裂及和田台阵位置见图1。图中Moho面深度数据来自滕吉文和曾融生（2002）的结果，震源机制来自万永革等（2010）及中国地震局地球物理研究所（2014）地震应急处置的结果。其中和田台阵位于和田地区皮山县，其外形轮廓为圆环形，由一个中心台和内、外环构成。台阵各子台都布设在同心圆环上，孔径为3km，属小孔径台阵。内环有3个子台，环半径约为600m：外环有5个子台，环半径约为1500m（图2a）。除中心台同时安装有一台CTS-1E-120s宽频带地震计和CMG-40T-1型地震计外，其余8个子台均安装频带为0.5～50Hz的CMG-40T-1型地震计。根据新疆地震台网编目的震中位置以及台阵中心台的坐标，计算出震中相对中心台的球面方位角为109.64°。为了对比研究，笔者利用台阵波振面方法重新计算该方位角。计算过程分两步：

（1）利用中心台CMG-40T-1型地震计记录的Z分量中首波Pn初至及其后10s的数据，对其余8个子台记录的波形进行互相关，计算这8个子台相对中心台的超越或延迟时间。

（2）以中心台为参考坐标，按0.01°步长进行全方位扫描，计算各个子步方位角所对应的入射波射线到8个子台的相对走时，并转换成与中心台的时差，与所计算出的互相关时差进行对比，找出二者总时差最小的入射线方位角。

利用互相关方法计算8个子台与中心台的时差时，分别对不同波形扫描时间长度进行了尝试，显示扫描时间长度为9～11s计算出的互相关时差比较稳定，其中扫描时间为10s的结果如图2a所示。由图可见，在震中方位上的子台，其相对到时为负，反方位上为正。0～360°扫描得出方位角为110.46°时，波射线到达各台的相对时差与互相关波形的时差相差最小，约0.0493s（图2b）。图2a中方括号内的数字为子台站号，方括号前数字为时间差。图2b中方括号内的数字为方位角，方括号上方数字为时间差，不同方位角上的半径长度对应于不同波射线时差与互相关时间差的绝对差值。本文得出的方位角110.46°与109.64°相差0.82°。进一步利用Matlab软件提供的reckon函数，求出距离中心子台327.952km（该值为中心子台与新疆地震台网所给的震中之间的球面大圆距离），方位角110.46°所对应的震中位置为（36.084°N，82.479°E），比新疆地震台网编目的结果偏西南4.714km，但它满足地震编目所要求的震中误差小于5km的一类精度水平。因此利用波形互相关方法可以较好地获取地震震中方位角，当震中距给定时，可以得出震中位置。从图2a还可以看出，震中与中心子台的连线几乎穿过4、6号子台。7、8、2号子台偏南，3、9、5号子台偏北。

2 台阵Pn段的高频时间不同步性分析

2.1 破裂过程穿透的两种可能介质模型

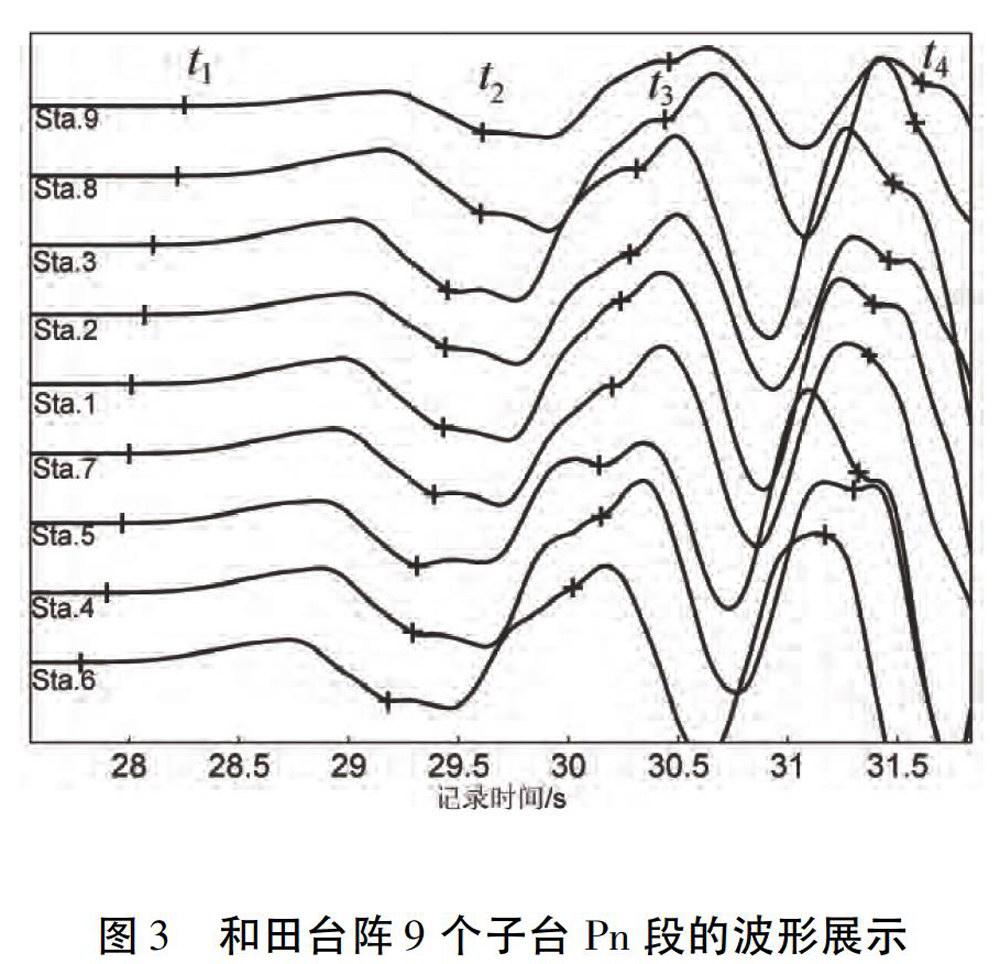
为了对比和田台阵各子台记录的Pn段的一些高频特征，前文已给出了不同子台的时差以及中心台入射线的方位角。将子台按到时的先后顺序显示Z分量（图3），图3中x轴时间跨度近4s。由于台阵距离震中约330km，地壳内显著的直达Pg波尚未到达，该时间段波形成分基本为首波。图3中除了t₁初至的起始点外，在1s左右大周期成分上存在约0.4s的小周期成分。由于数据采样率为100点/s，利用MSDP软件，将波形放大到可以识别0.01s的极限显示精度。根据t₁、t₂、t₃、t₄（t_i分别为几个压缩波形的起始时刻）附近的曲线拐点情况、曲线变化形态及9个台站间波形对比，逐点分析局部时间的幅值变化，从而精细提取各个子台每个小周期成分的起始时刻t_i，j（其中i为1～4不同时刻，j为1～9子台号），并用“+”标记在相应的波形上。图4中将子台号标注在横坐标轴上，且图4的台号顺序是以垂直入射线（图2）从西南往东北按距入射线远近依次排列，以利于从入射线切线方向分析到时差异。t₄之后约1s，Pg震相族抵达台阵，波形变得复杂化。由于Pg初至对应的破裂点早于t₄处Pn对应的破裂点，Pg、Pn地壳速度模型的可靠性对其分析结果有较大影响，因此未考虑后续的细节震相。

由图3可以发现，不同时刻点上的“+”有一定的时间交错性。为此，每个时刻点上9个子台都减去子台6的到时，将结果绘于图4a。由图4a可看出，不同震中距具有一定的走时差异，且后3个时刻的高频成分走时整体略低。图4b是在图4a的基础上再将t₁时刻的各个子台时差对应相减。经过两次减法，基本扣除了每个子台GPS授时误差及台阵各子台之间距离的影响。图4b显示3条曲线几乎都小于0，而且沿垂直于波射线排列的子台所获取的差值呈“n”型分布，表明后3组波动到6号子台的相对时间比第1组到达的相对时间减少了。引起这种现象可能有3种因素：①人工提取各个压缩波形初至到时引入了人为误差；②从震源传播到台阵的射线路径上存在着横切路径的强烈的横向速度扰动，引起一些非均匀相移；③震源破裂过程中，不同时刻破裂点所处的介质波速参数存在空间分布差异而引起相移。

对于第①种因素，笔者认为肯定存在拾取误差，但该误差应呈现非相关特征，不会出现“∩”型分布。对比图2a和图3，发现人工提取的初始时间和互相关方法给出的序列并不一致，特别是4、5号子台的顺序。这种差异可能是做互相关时使用了10s的时间，在这个时段中震源破裂点已出现位置变化，5号子台更早接收到后续破裂点的震动。2、3号子台也有类似的现象。而发生这个现象的台站主要分布于相对中心台与震中连线近似对称的位置。对于第②种因素，在2.2节进一步分析。

对于第③种因素，给出以下模型。因为和田台阵属小孔径台阵，直径约3km，震中距328km，台阵对震源的张角很小（约0.524。）。射线在震源体之外的传播过程中几乎穿透相同的介质，会引起后3组时差变小，最有可能源于震源破裂点附近的介质参数在空间分布上的变化。假定3种情况：（1）震源破裂点下部的各向异性差异减少；（2）震源破裂点上部的各向异性差异减少；（3）震源破裂点上下部的各向异性差异不变。

图5中，保持模型c参数不变，以作对比。破裂过程都由黑点向白点扩展；每方格的高度为1，方格上的数字对应速度比值；黑色箭头为Pn传播方向。模型b中，破裂点从下往上破裂，而首波都是朝下传播，因此这里的箭头使用虚线，以示区别。3种模型的Pn穿透不同参数的两个方格厚度后的时差分别为：模型a：1.3409；模型b：1.8333；模型c：2。

因此只要在破裂过程中，破裂点扩展的后期介质参数比前期的参数（这里指P波波速）更趋于相近时，则从不同时刻传出的首波震动到达台阵各子台的时间将趋近。如果破裂后期的介质参数差异大于前期，那将大于模型c的值，不满足图4b中所显示的现象。由于在各向同性线弹性模型中，介质波速与介质参数关系式为V_p=？其中，λ、μ为拉梅常数，分别反映压缩膨胀效应和剪切形变效应；ρ为介质密度，对于地壳介质，λ、μ的垂向变化一般较ρ明显。因此推测于田M_S7.3地震很可能符合（1）、（2）其中的一种情况，破裂点都有由破裂面上各向异性较强的点位向各向异性趋同的点位扩展的过程，在此过程中出现了疑似障碍体或凹凸体。障碍体指高临界强度区，也可以是断层面上的一些二级凹凸面（Aki，1979），凹凸体指应力集中区（宫武隆，1993；Dragoni，Piombo，1998）的特征。在笔者研究的这4s时间内，破裂点由各向异性较强（如水平差异导致的垂向组合分布）的点位向较弱点位过渡，每个破裂点的子震源在这个时间段内依次产生并传播首波，但后续破裂点的首波所经过的射线上的介质差异减弱，从而出现后续子破裂的首波走时更接近。实际上，在精细的破裂过程反演计算中，障碍体破裂过程的滑动幅度与其断层相应位置处的刚度有一定的模型关系（何玉梅，郑天愉，1998）。这种反演方法上对刚度的差异性设置，与图5的速度垂向异性简化模型都属于刻画震源体内部的各向异性特征。至于于田主震破裂方式是从上往下，还是从下往上，笔者没有搜集到更多的同精度的资料供分析。由于时差呈“∩”型分布，不是单斜曲线，不支持该短暂破裂过程只朝单侧进行的情况，因此笔者着重讨论由水平分异引起的垂向介质参数差异。而张广伟等（2014）反演的结果也显示此次大地震破裂面比较集中，水平两侧扩展的尺度不明显。

2.2 关于震源区以外速度界面影响的分析

进一步讨论2.1节中第②种因素的影响。不只传播路径上的速度间断面可以衍生震相，地震计的瞬态反应如果没有有效的阻尼作用，也将出现拖尾现象。对于地震仪器的因素，由于同台的瞬态响应不变，因此如果存在后续“拖尾”震相，这些震相应该是等间隔的，不会出现“∩”型分布。而对于速度界面的影响，引入震中距58km的于田（YUT）台站波形进行分析。同时为了进一步对比，还引入了一个震中距与之相近（56km）、位错为走滑兼正断性质的、且位于初动向上的小震波形。该波形为北京南山村（NSC）台的记录的2012年6月18日天津宝坻M_S4.0地震的波形（震源机制解：走向142°，倾角87°，滑动角-15°）。由于天津有近50个强震加速度计获取了相应的烈度分布，可以确定该地震为北西向破裂，所以与之共轭的北东向震源机制解舍弃。使用这个对比地震同时还考虑到4级地震破裂过程简单。

图6中将原始记录的EW、NS分量旋转成T、R分量，以确认于田台站记录的直达剪切波sg初至。对比图6b、f，NSC台记录的Sg-Pg比YUT的台记录的略小，但都接近8s，反映出二者震中距的大小。由于宝坻Ms4.0地震破裂尺度小，在图6e～g中可以明显看出，在Pg之后，Sg之前，波形幅度明显比Pg前2个周期的振幅小。而且在这个震中距，反射震相P^*、P₁₁尚不发育，因此Pg振幅占绝对优势。而于田M_S7.3地震破裂面尺度可达50×15km（陈运泰，顾浩鼎，2004），若以0.8倍的横波速度破裂，破裂10km尺度也需约3.125s（破裂速度假定为3.2km/s）。因此笔者在局部放大图6d中发现，波幅强度呈增长趋势，特别是图6c中的Px处出现了一个更显著的介质破裂。由此推测，即使在于田地震破裂的前3s内也存在多个级联子破裂，与永善大震破裂过程类似（曾融生，师洁珊，1978）。而位于震中距328km处的和田台阵记录的Pn波形中捕捉了这些级联破裂的某些初动曲线拐点。

由于一个大地震破裂的过程是不均匀的，每次子破裂点的位置在横向和纵向上都不一样。破裂过程中震源区介质的性质（弹性、均匀性、各向异性）都将发生变化，关于台阵子台时差现象的分析，除了上述3种情况外，是否还有另外的解释？这里引入两个概念：一是震源区静态的各向异性分布；二是地震发生过程伴随时间变化的局部性质瞬态改变。第一种情况为图5所示情形。对于随着破裂过程而产生的介质性质瞬态变化，如果破裂点外的介质均匀或水平层状均匀，则这个子破裂产生的波源传到台阵各子台的时间变化较少，难以观测，或呈单斜曲线。因为从其震源机制解可知，断层面倾角约82°，而本文研究的子破裂间隔约1s，如果是位错在入射面上的水平破裂分量引发的波速扰动所致（水平层状均匀，垂直分量不产生此效应），当破裂速度取3.2km/s，震源体附近地壳P波速度6.2km/s，速度扰动为10%时，两次破裂的各子台对应时差为0.0018s。这个量值在采样率为100点/s观察不到。

而对于水平成层介质，垂直入射面的位错破裂分量引发的介质P波速度变化，对各子台的相对时差无影响，即沿入射面法向的介质瞬态变化对各子台相对走时无影响（处于同一平面波阵面同等相移不影响各子台的相对到时）。对于水平单向破裂，则需进一步分析。根据图1断裂走向及震源机制解，取破裂面走向239°，且假定本文研究的短时间破裂过程中，破裂面走向不变，根据震中相对各子台的方位角，求出图7a中各子台的θ，进而可以利用破裂长度d₁、d'₁，计算出P₂、P₃到子台i的走时与原路径L₀走时差。先假定破裂由P₁向西南破裂10km到达P₂，破裂过程介质力学性质发生瞬时改变，可以产生10%的P波速度扰动，则以0.9倍的P波速度穿过L₀-L₁的时间差，如图7b的Linel曲线所示（减去了最小变化的7号子台走时差，括号里的数值是7号的相对走时差），以1.1倍P波速度穿过L₀-L₁的时间差，如图7b的Line2曲线所示。而由P₁向东北破裂10km到达P₃的两个速度计算的走时差曲线分别为Line3、Line4。计算表明，在10%速度扰动的情况下，要使该台阵子台的相对走时差达到0.01s的识别水平，破裂长度应不小于10km。因此对于本文研究的3～4s的波形长度，即使存在单侧破裂，从P波信息里也仅仅能略有反映，但不明显。不过对于单侧破裂，各子台的相对走时是单斜型曲线。从Line1、Line2等后括号内数字对比还可显示，向西南破裂引起的相对走时差略小于向东北破裂，这是因为台阵位于震中西北，而破裂走向为北东，向东南破裂时，新破裂点到各子台的距离都减小了（图7a）。因此，对比图4b与图7b的走时差量级，笔者认为震源区应存在“静态”的各向异性（图5a、b），才能出现较符合子台相对走时差减少的特征。如果弹性模量值较大区与较小区的P波速度差异为10%，则要产生本文可观测时差（如0.04s）的弹性异常体尺度约1.23km（与入射面平行的方向）。如果弹性模量值较大区与较小区的P波速度差异为2%，则产生本文可观测时差的弹性异常体尺度约6.19km（条件同上）。对于于田地震，当震源体附近存在各向异性时，产生同等速度扰动的各向异性体尺度要比单侧破裂的长度小若干倍。本文观测到的时差量级更倾向于震源体附近存在各向异性体的结论。

3 结论与讨论

本文利用和田台阵的地震资料对2014年于田M_S7.3地震前4s的破裂过程进行了细致分析。利用中心子台与震中的连线确定台阵中各个子台的相对位置。在此基础上对子台波形进行特定排序，并提取了不同时刻点上的成组高频压缩波初至。这些初至走时之间的相互差异反映了一些震源破裂点处的介质特性。为进一步讨论这些特性的可能分布，利用宝坻地震的NSC台资料与于田地震的于田台资料进行对比，结果反映和田台阵记录的Pn段内确实存在多级级联破裂现象。如果早期破裂点处的各向异性差异大于后续破裂点（只分析了3s）的差异，则可以更好解释本文提取到的“∩”型时间分布现象。这也说明了和田台阵记录到了这个大地震最初破裂区的一些级联破裂的凹凸体或障碍体特征。若利用图4b中的3、9、5子台时差比其他子台更小的细微差异，则可进一步推测后续破裂点将向南偏移，使得位于入射线北部的子台经过更长路径的各向异性较弱的区域，从而降低相对时差。这与中国地震局地球物理研究所应急处置给出的破裂过程反演分布中往南往深部扩展的特征相吻合，同时也与张广伟等（2014）复杂反演的往南破裂结果吻合。

由于和田台阵距离震中还是较远，一些近场高频成分未能有效记录。对高频成分的人工提取位置也不能认定其必然很可靠。因此本文的结论还需要收集更多的近场台阵资料或相关类似资料进行判定。但利用台阵获取大震破裂过程的细微特征，这项工作是非常值得去研究的。

非常感谢在2014年于田地震应急工作中，新疆维吾尔自治区地震局蔚晓利研究员及唐明帅博士给予的帮助。同时感谢审稿老师对初稿的修改建议。