基于水热耦合平衡理论的嫩江流域蒸散发估算

李鸿雁， 薛丽君， 王世界， 安丰亮

(吉林大学 环境与资源学院，吉林 长春 130021)



基于水热耦合平衡理论的嫩江流域蒸散发估算

李鸿雁， 薛丽君， 王世界， 安丰亮

(吉林大学 环境与资源学院，吉林 长春 130021)

由于区域蒸散发时空变异性较大，难以采用点位监测方法来测定，因此，流域蒸散发估算是目前水文学领域的难点和重点问题。从水热耦合平衡理论入手，采用傅抱璞公式估算嫩江流域及典型汇水区的实际蒸散发。结果表明，傅抱璞公式的逐年蒸散发估算结果具有较高精度，且干燥度较大的汇水区的估算结果精度较高。然后，对嫩江流域蒸散发进行时空演化分析。结果表明：在1956—2000年，年实际蒸散发和潜在蒸散发均无趋势性变化；在2000—2013年，多年平均实际蒸散发与潜在蒸散发在空间上呈相反分布，整体上从上游至下游递减(递增)。最后，分析了下垫面参数w的分布规律，其表现为由上游至下游随植被覆盖率的减小而减小的特征。研究表明，傅抱璞公式为流域的蒸散发估算提供了可靠的方法，对于流域水资源预测和生态需水推求等具有十分重要的意义。

水热耦合平衡；Budyko公式；傅抱璞公式；嫩江流域；蒸散发

流域的蒸散发是水文循环的重要环节，由于下垫面水热条件复杂多变，无法通过定点监测来推求。因此，如何获得准确的区域蒸散发成为水文学研究中的难点问题。自从1982年Dalton提出著名的道尔顿蒸发定律开始，近代的蒸发理论逐步形成[1]，此后，众多学者致力于探索区域蒸散发的估算方法。各种估算方法可分类为：①微气象学方法，包括波文比-能量平衡法[2]、涡度相关法[3]和空气动力学法[4]，这些方法以计算机科学和气象科学为基础，通过数据的自动采集与系统处理，对区域的蒸散发进行估算。②遥感技术，其优势是具有时空的连续性，能准确地描述地表特征，对于区域的小时空尺度的蒸散发研究具有重要意义。③气候学方法，以气象数据为主要输入参数的蒸散发估算公式和模型，典型方法包括Penman公式[5]和Bouchet互补相关模型[6]，并产生了Penman正比假设(实际蒸散发与蒸散发能力成正比关系)和Bouchet互补假设(实际蒸散发与蒸散发能力成互补关系)。④水文学方法，包括水量平衡法和水热平衡法。水量平衡法在多年尺度上有着相当高的精度，常作为其他估算方法的验证标准；水热平衡法综合考虑水量和热量，认为蒸散发同时受到降水量和潜在蒸散发的控制。水热平衡法中最具代表性的是Budyko水热耦合平衡理论，Budyko公式一经提出，就在多个区域应用，均得到了较好的结果[7-9]。1981年，傅抱璞公式[10]的建立将Budyko公式完善推广，并在我国广大地区得到了良好的应用[11-12]。

本文采用基于水热耦合平衡理论的傅抱璞公式估算嫩江流域及典型汇水区的实际蒸散发量，与水量平衡法的结果进行比较分析，以评价该方法在流域的适用性。该研究对嫩江流域水资源的预测和科学管理具有重要意义，同时为半湿润地区的蒸散发估算提供了借鉴。

1　水热耦合平衡理论

Budyko[13-14]认为在年时间尺度上，流域蒸散发同时受降水和潜在蒸散发两个因素控制。在年或多年尺度上，可用降水量代表水量供给条件，潜在蒸散发量代表能量供给条件，对陆面蒸散发限定了如下边界条件[15]。

①在干旱条件下：

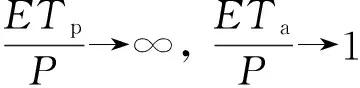
②在湿润条件下：

式中：ETa为实际蒸散发量，mm；ETp为潜在蒸散发量，mm；P为降水量，mm。

由此表明，在干旱条件下，潜在蒸散发量大于降水量，全部降水量转化为蒸发量；在湿润条件下，降水供给量大于潜在蒸散发量，可用于蒸散发的能量都将转化为潜热。

能够满足条件①和②的函数应具有如下形式：

或

(1)

式(1)即为Budyko公式，也是水热耦合平衡方程的一般形式。

1904年，德国水文学家Schreiber[16]对欧洲河流的降水径流数据进行分析研究时指出，随着流域降水量的增加，流域径流量也随之增加，并且在数值上无限趋近于降水量，却始终无法达到降水量。基于

以上研究，Schreiber提出了如下公式：

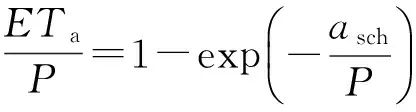
(2)

式中asch为一有量纲参数，mm/a。

1911年，俄国著名学者Ol′dekop[17]在Schreiber理论的基础之上，采用多年平均潜在蒸散发ETp修改公式(2)，得到公式(3)：

(3)

通过与水量平衡对比分析，Budyko发现Schreiber公式计算值偏小，Ol′dekop计算公式偏大，如图1所示。Budyko对Schreiber曲线和Ol′dekop曲线进行了几何平均，得到了Budyko曲线，其数学表达式如下：

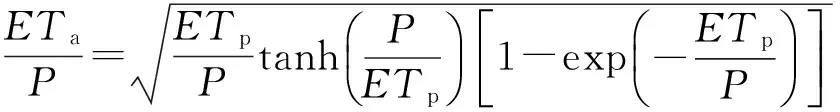
(4)

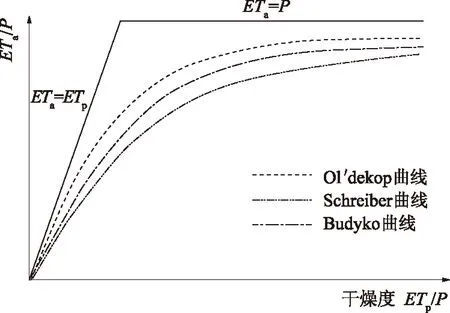
图1　水热耦合平衡曲线示意图

此后，Budyko公式陆续出现了许多不同形式的数学表达式[18-21]，见表1，其中以傅抱璞公式应用最为广泛，本文采用傅抱璞公式进行嫩江流域蒸散发的估算。

表1　Budyko及其改进公式

2　工程应用

2.1研究区概况及数据资料

嫩江流域是松花江北源，发源于北部的大兴安岭伊勒呼里山，在吉林松原三岔河汇入松花江，全长1 370 km，流域面积29.7万km2，地跨黑龙江、吉林、内蒙古三省区，地理坐标119°12′～127°54′E、44°02′～50°36′N，该流域北部、西部和南部三面地势较高，东部地势较低，形成著名的松嫩平原。嫩江流域属寒温带半湿润大陆性气候，冬季寒冷、夏季温热，春秋多风少雨，四季分明，冷热悬殊；多年平均降水量为400～500 mm，最大降水量为937.4 mm，最小降水量为152.5 mm，年降水量主要集中在6—9月份，约占全年降水量的82%，其中7、8月份2个月所占比重最大；年水面蒸发量为1 000～1 600 mm，受地形影响，上游山区蒸发量低于下游平原区。

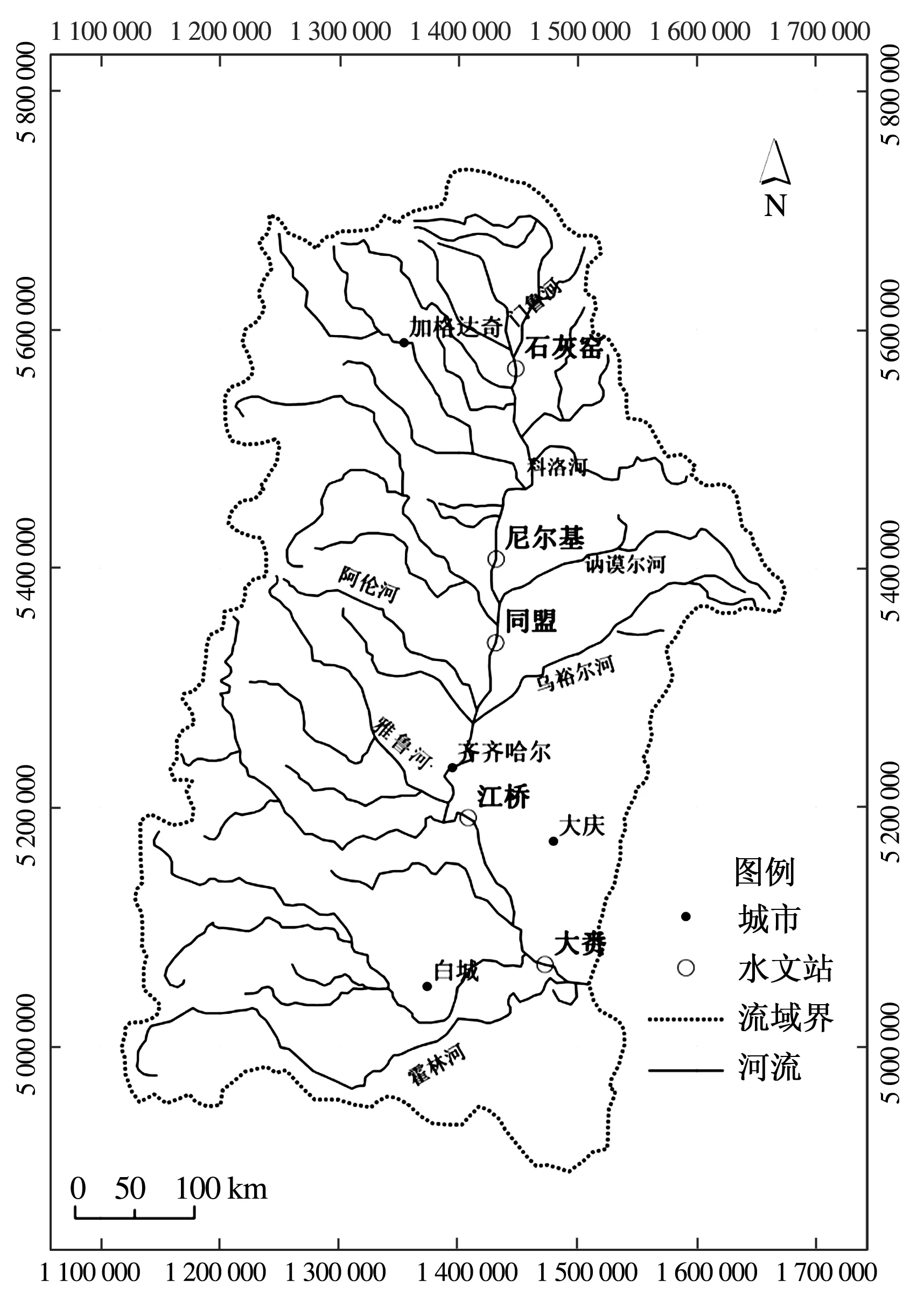
图2　嫩江流域水系图

本文采用的数据有嫩江流域降雨径流数据、DEM数据以及流域内气象站数据。主要数据来源有：①降雨径流资料(水利部松辽水利委员会水文局水文信息中心提供)为嫩江干流典型水文站(石灰窑、同盟、大赉水文站)1956—2000年近50年的数据资料；②土地利用资料(中科院数据共享网提供)为嫩江流域20世纪80年代、90年代和2000年3期1∶10万土地利用数据；③DEM数据(CGIAR提供)为90 m精度DEM数据；④气象数据(中国气象科学数据共享服务网提供)为嫩江流域气象站气温、风速等气象数据。

2.2研究方法

根据傅抱璞公式估算嫩江流域1956—2000年逐年蒸散发，在计算过程中，潜在蒸散发采用FAO Penman-Monteith修正公式计算，先计算每个气象站点的日潜在蒸散发；然后利用ArcGIS软件统计为整个流域的面平均值，再将日数据整理为年数据，得到面的逐年潜在蒸散发数据；最后采用水量平衡法计算流域蒸散发，作为检验傅抱璞公式计算结果的标准。

2.2.1基于傅抱璞公式的蒸散发计算方法

即使在多年平均条件下，流域水量平衡也会受到除气候外其他因素(如土壤、植被等)的影响。Budyko水热耦合平衡理论最初应用于流域蒸散发的研究，并未考虑到下垫面条件，影响了其估算精度。因此，如何引入考虑下垫面因素的Budyko水热耦合平衡方程，是长久以来众多学者研究的重点和难点问题。

1981年，我国著名气候学家傅抱璞先生以Budyko水热耦合平衡原理为基本理论，充分考虑下垫面条件，通过量纲分析和数学推导，根据流域水文气象的物理意义提出了如下公式：

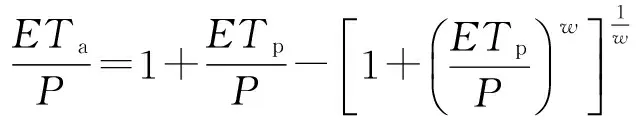
(5)

或

(6)

式中w为无量纲积分常数，反映了区域间的差异，且w∈(1,∞)。

公式(5)和公式(6)即为傅抱璞公式，其准确地反映了P(供水条件)、ETp(能量条件)和ETa(流域蒸散发)之间的关系，傅抱璞公式将Budyko理论定量化，是Budyko理论的解析表达式，具有扎实的物理基础，对于Budyko理论的推广应用意义重大。

2.2.2潜在蒸散发计算方法

根据《中华人民共和国气象行业标准》，FAO Penman-Monteith公式是联合国粮农组织推荐使用的具有相对较小误差的计算潜在蒸散发量的方法，FAO Penman-Monteith修正公式表达如下[22]：

(7)

式中：以日为计算时段，ETp为日潜在蒸散发量，mm·d-1；Rn为日地表净辐射量，MJ·m-2·d-1；G为日土壤热通量，MJ·m-2·d-1，当时间尺度为日或以上时，G=0；T为2 m高处日平均气温，℃；U2为2 m高处风速，ms-1；es为饱和水气压，kPa；ea为实际水气压，kPa；Δ为饱和水气压曲线斜率，kPa·℃-1；γ为干湿表常数，kPa·℃-1。

本文采用FAO Penman-Monteith修正公式计算流域内各气象站点的潜在蒸散发，公式中各分量的计算方法和计算步骤均参考《中华人民共和国气象行业标准》。

2.2.3基于水量平衡法的蒸散发计算方法

水量平衡法是计算流域蒸散发的最基本方法，遵循质量守恒定律。在闭合流域内，若不考虑相邻区域水量的调入与调出，其水量平衡方程可以写成：

ETa=P-R+ΔW。

(8)

式中：ΔW为蓄水变化量，mm；R为径流量，mm。

对于多年平均和年尺度，流域的蓄水量变化可以忽略，因此流域的年水量平衡方程可以写成：

ETa=P-R。

(9)

迄今为止，水量平衡法仍是估算长时间尺度流域蒸散发的最可靠方法[23]，本文采用水量平衡法评价傅抱璞公式的计算精度。

2.3结果与分析

2.3.1嫩江流域逐年蒸散发估算

点绘(ETa/P)-(ETp/P)和(ETa/ETp)-(P/ETp)于图3和图4中。由图可以看出，嫩江流域符合Budyko基本曲线。公式中的参数w采用嫩江流域多年平均水文数据由水量平衡法反推获得，经计算分析，w=2.16。对比傅抱璞公式和水量平衡法的计算结果，二者拟合情况较好，误差较小，结果如图5(a)所示。为更直观地反映傅抱璞公式与水量平衡法计算结果的关系，绘制图5(b)。由图5(b)可以看出，傅抱璞公式与水量平衡法的计算结果基本位于45°趋势线附近，证明傅抱璞公式估算结果精度较好。

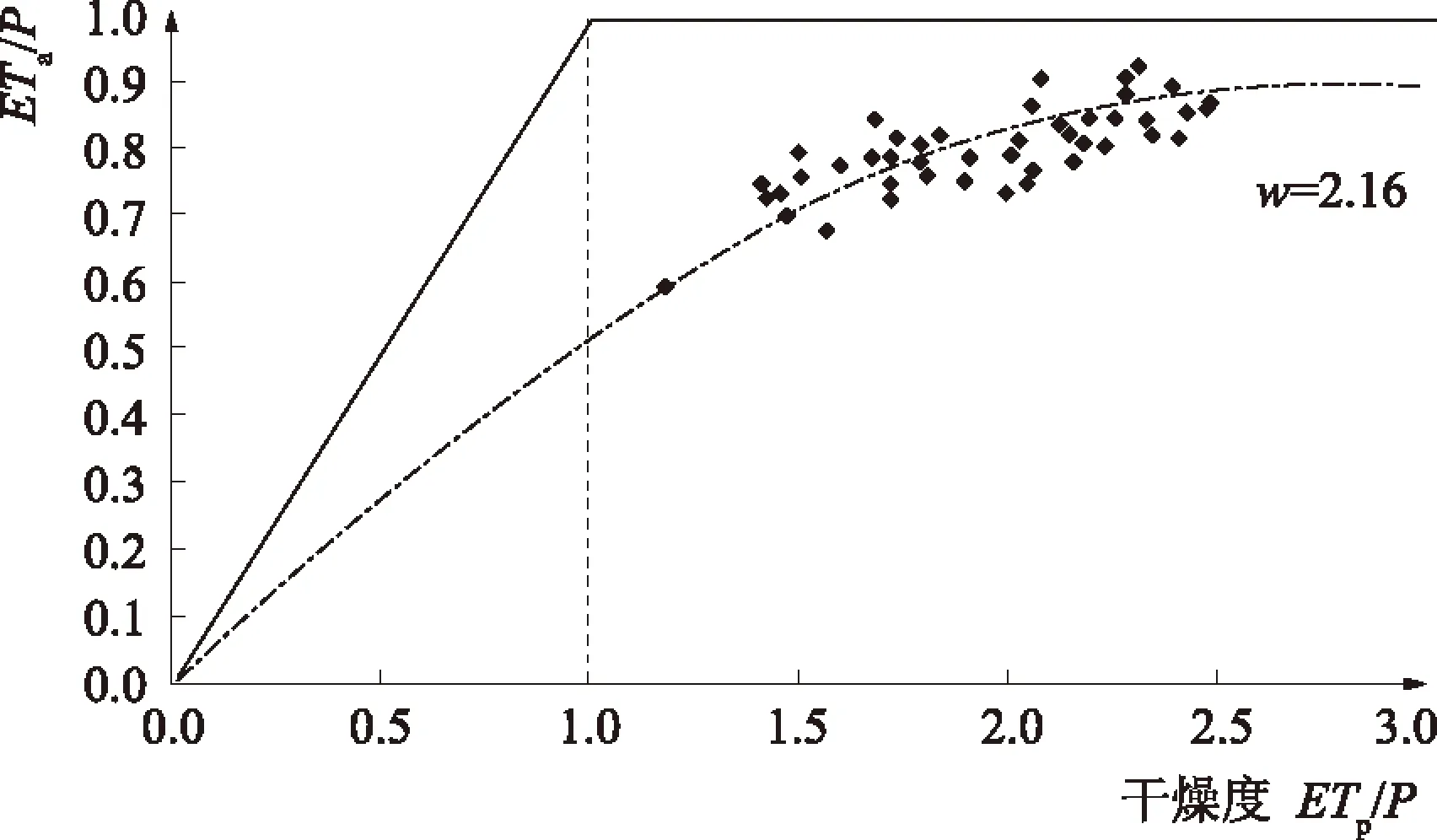
图3　嫩江流域干燥度曲线

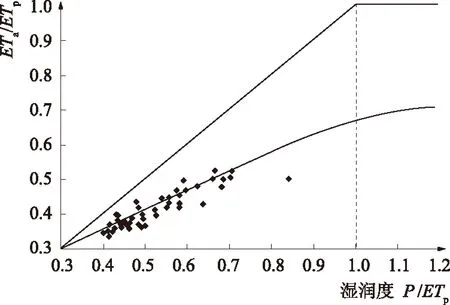
图4　嫩江流域湿润度曲线

(a) 水量平衡法与傅抱璞公式计算结果比较(b) 水量平衡法与傅抱璞公式计算结果的关系

图5嫩江流域蒸散发估算结果比较

2.3.2典型汇水区逐年蒸散发估算

与嫩江流域相同，绘制1963—1987年各典型汇水区(石灰窑、同盟、大赉)水量平衡法计算结果与傅抱璞公式估算结果的比较曲线，如图6—8所示。

由图6—8可以看出，各典型汇水区逐年蒸散发的水量平衡法计算结果与傅抱璞公式估算结果的拟合情况也较好，且存在着从上游至下游拟合度越来越高的规律。傅抱璞公式中的参数w均采用各典型汇水区多年平均水文数据由水量平衡法反推获得。

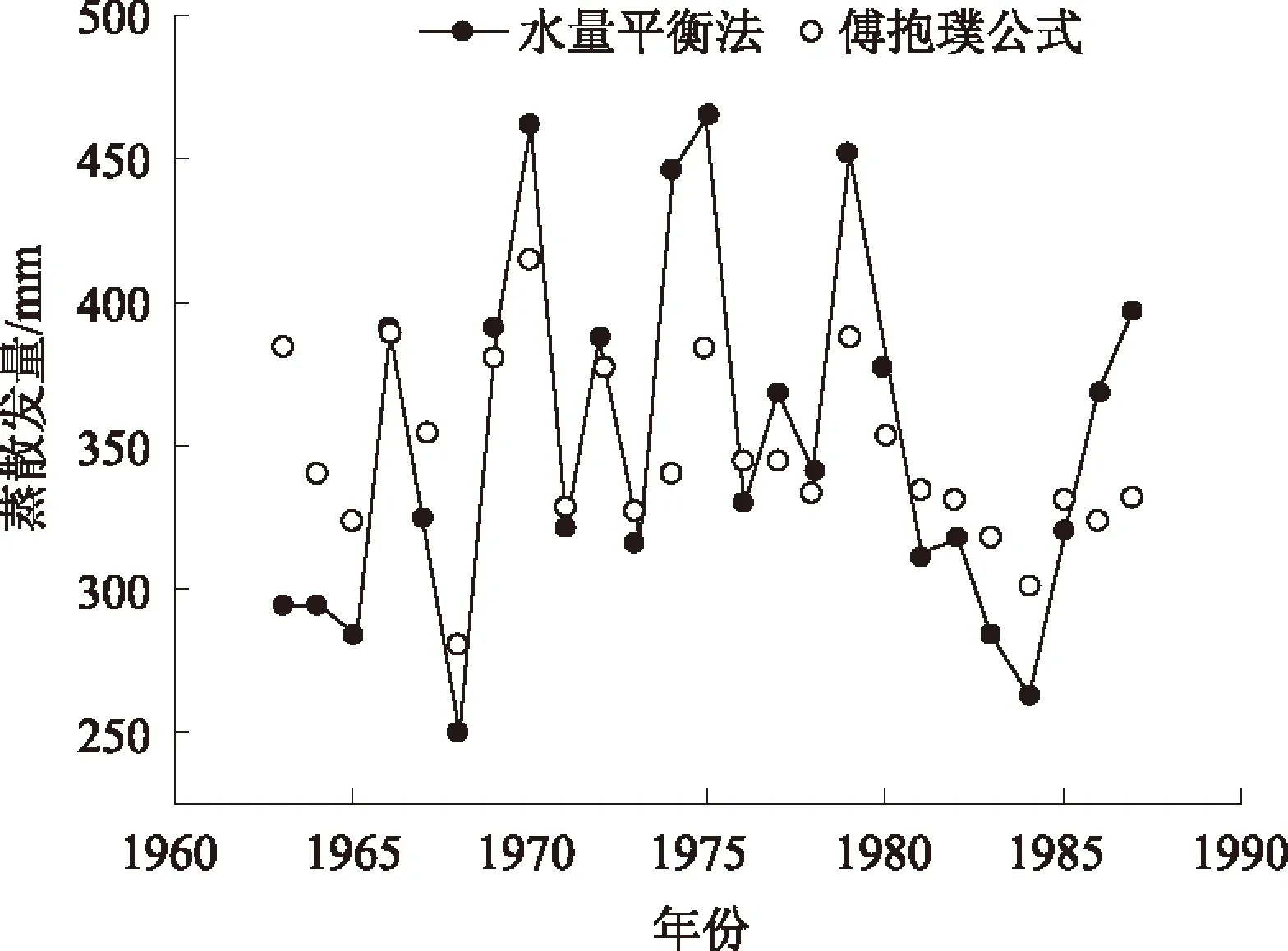
图6　石灰窑汇水区蒸散发估算结果比较

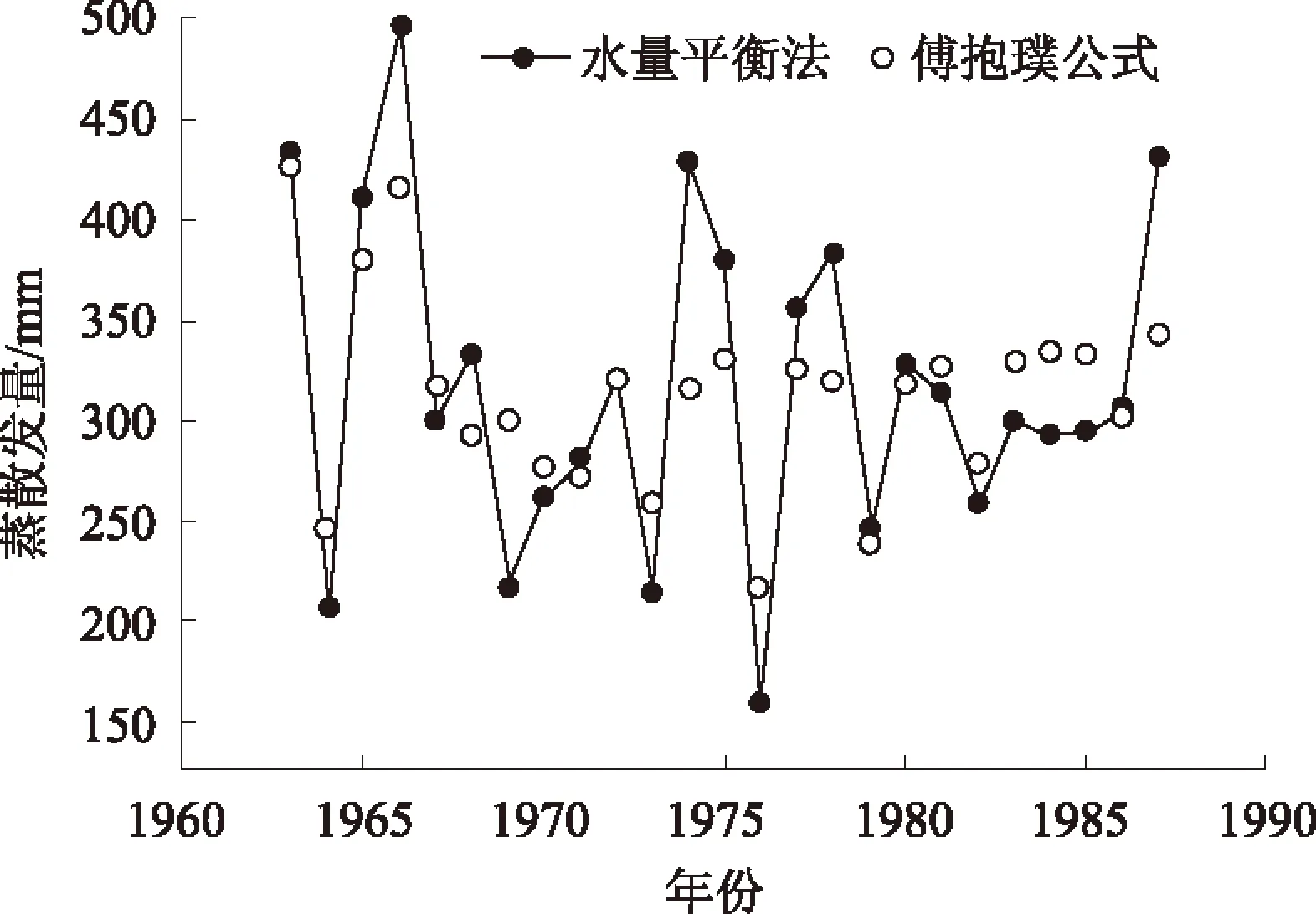
图7　同盟汇水区蒸散发估算结果比较

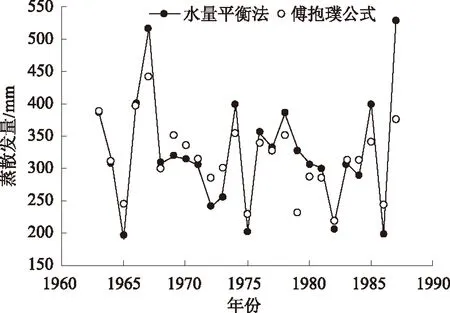
图8　大赉汇水区蒸散发估算结果比较

2.4误差分析

根据计算结果，采用相对误差RE进行误差分析，并采用纳西效率系数NSE和相关系数R进一步对两种方法的计算结果进行比较。

(10)

式中：E傅为傅抱璞公式估算的年蒸散发量，mm；E水为由水量平衡法计算的年蒸散发量，mm。

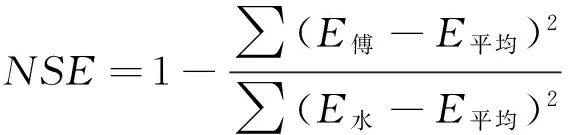
(11)

式中E平均为水量平衡法计算的多年平均蒸散发量，mm。

(12)

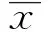
通过计算，对于嫩江流域逐年尺度，除个别年份(1960年、1989年、1998年)外，其余各年相对误差均控制在10%以内，纳西效率系数NSE为0.71，相关系数R2为0.86，达到α=0.001显著水平。可见，傅抱璞公式估算结果与水量平衡法计算结果拟合情况较好。

采用嫩江流域石灰窑、同盟和大赉水文站1963—1987年的水文气象数据进行逐年蒸散发估算，其误差结果见表2。

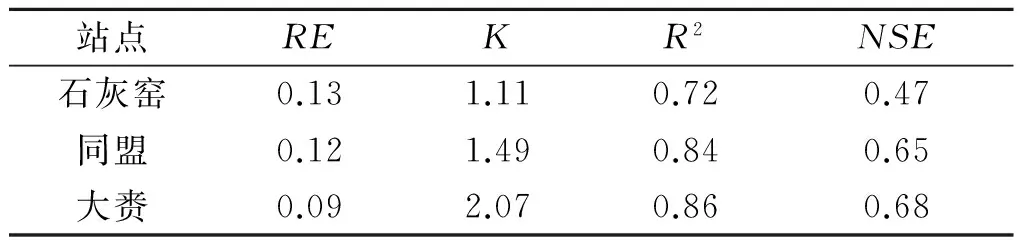
表2　嫩江流域各典型汇水区年蒸散发估算误差分析

注:K=ETp/P，是干燥度(Drought Index)，用以表征气候干燥程度。

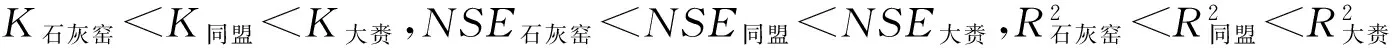
3　嫩江流域蒸散发时空演化分析

3.1蒸散发时程演化趋势

根据上文计算获得的蒸散发数据，绘制年蒸散发和潜在蒸散发的时间序列图，如图9所示。

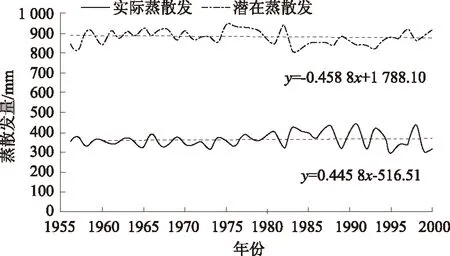
图9　实际蒸散发量和潜在蒸散发量的时间序列图

采用Mann-Kedall 非参数检验法进行趋势性检验。结果表明：在α=0.05的显著性水平下，均未通过95%的置信度检验，证明1956—2000年间，年蒸散发和潜在蒸散发均没有趋势性变化。

3.2蒸散发空间演化规律

为更加直观地描述嫩江流域2000—2013年多年平均蒸散发与潜在蒸散发在空间尺度上的分布，本文采用MODIS16遥感数据，利用ArcGIS软件解析遥感卫星影像得到嫩江流域蒸散发与潜在蒸散发的空间分布图，分别如图10和图11所示。由图10和图11可以看出：蒸散发从上游至下游逐渐下降，潜在蒸散发从上游至下游逐渐上升，整体呈现西北到东南的递减(递增)趋势。

图10　嫩江流域蒸散发量的空间分布(单位：mm)

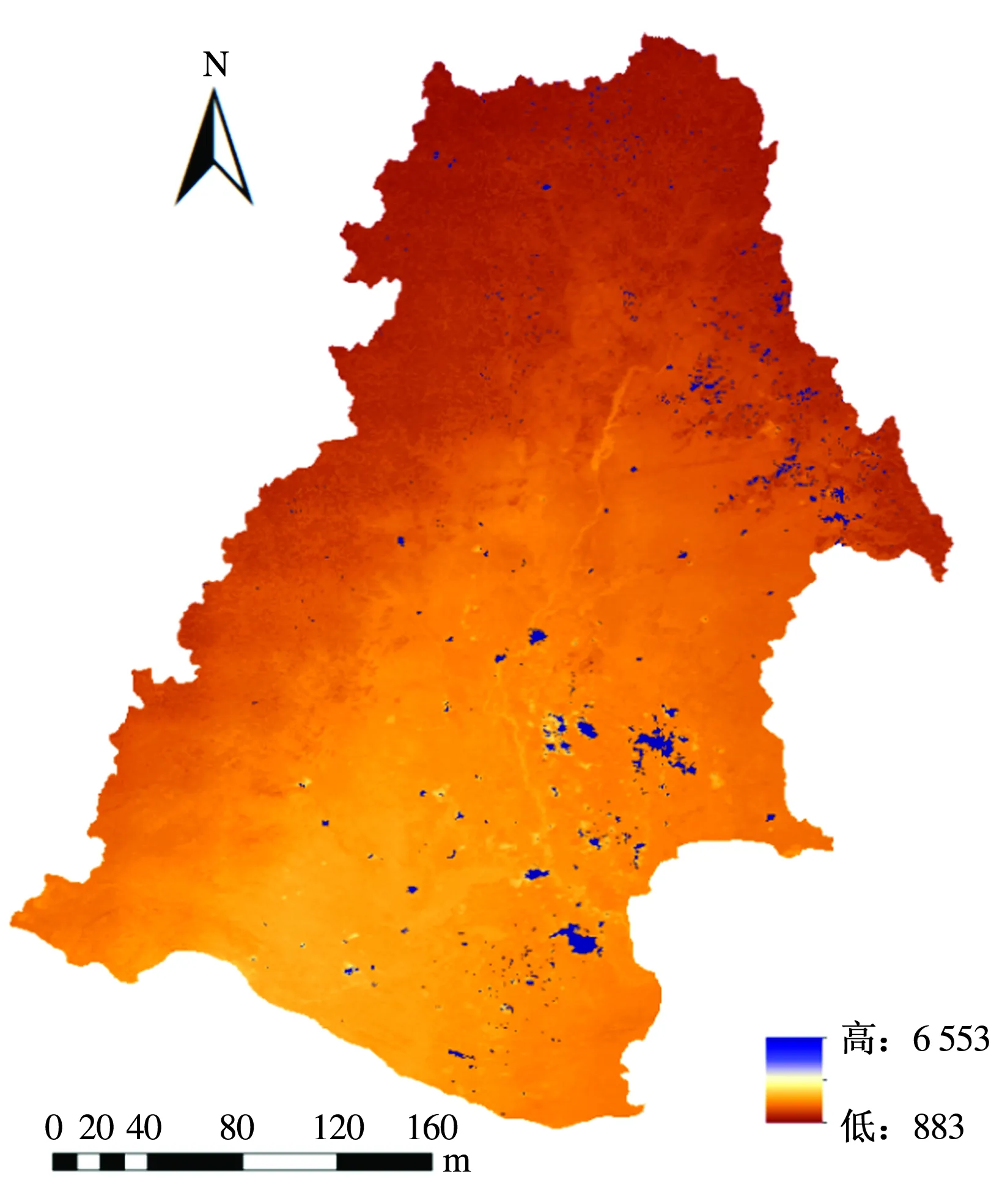
图11　嫩江流域潜在蒸散发量的空间分布(单位：mm)

3.3参数w的估算及空间分布特征

参数w反映了影响蒸散发的下垫面特征，可以采用多年平均水量平衡反推的方法进行计算。分析典型水文站石灰窑、同盟、大赉的参数w值，可得：w石灰窑>w同盟>w大赉，由上游至下游w值变小。同时，嫩江流域的植被覆盖率f石灰窑>f同盟>f大赉，由上游至下游f值变小，因此下垫面参数w随植被覆盖率f的增大而增大。由此证明，在嫩江流域，参数w反映了流域的下垫面特征(主要是植被特征)。

4　结语

1)嫩江流域逐年实际蒸散发量的估算。对比傅抱璞公式估算结果和水量平衡法计算结果，除个别年份(1960年、1989年和1998年)外，其余各年误差均控制在10%以内，相关系数R2为0.86，纳西效率系数NSE为0.71，结果精度较高。

2)石灰窑、同盟和大赉水文站逐年蒸散发量估算结果表明，嫩江流域从上游至下游，随着干燥度的不断增大，纳西效率系数增加，相关系数也增加，表明在干燥度较大的汇水区，傅抱璞公式估算精度较高。

3)嫩江流域蒸散发的时间演化和空间分布。在α=0.05的显著性水平下，1956—2000年间，实际蒸散发和潜在蒸散发均没有趋势性变化；2000—2013年间，多年平均实际蒸散发与潜在蒸散发在空间上呈相反分布，整体由上游至下游递减(递增)。

4)下垫面参数w分布特征。从上游到下游，w随植被覆盖率f的减小而减小。

[1]张薇.河套平原蒸发蒸腾量时空反演研究[D].北京：中国地质科学院，2008.

[2]BOWEN I S.The ratio of heat losses by conduction and by evaporation from any water surface[J].Physical Review,1926,27:779-789.

[3]SWINBANK W C.The measurement of vertical transfer of heat and water vapor by eddies in the lower atmosphere[J].J Meteor,1951,8:135-145.

[4]THORNTHWAITE C W,HOLZMAN A.Report of the commutation on transpiration and evaporation[J].Transactions of the American Geophysical Union,1944,25:683-693.

[5]PENMAN H L.Natural evaporation from open water,bare soil and grass[J].Proceedings of the Royal Society of London,1948,193(1032):120-145.

[6]BOUCHET R J.Evapotranspiration réelle et potentielle,signification climatique[J].IAHS Publ,1963,62:134-142.

[7]韩松俊,胡和平,田富强.基于水热耦合平衡的塔里木盆地绿洲的年蒸散发[J].清华大学学报:自然科学版, 2008,48(12):2070-2073.

[8]高国栋,陆渝蓉,李怀瑾.我国最大可能蒸发量的计算和分布[J].地理学报,1978,33(2):102-107.

[9]LI Changbin,ZHANG Xuelei,QI Jiaguo,et al.A case study of regional eco-hydrological characteristics in the Tao River Basin,northwestern China,based on evapotranspiration estimated by a coupled Budyko Equation-crop coefficient approach [J].Science China Earth Sciences,2015,58(11):2103-2112.

[10]傅抱璞.论陆面蒸发的计算[J].大气科学,1981(1):23-31.

[11]孙福宝,杨大文,刘志雨,等.海河及西北内陆河流域的水热平衡研究[J].水文,2007,27(2):7-10.

[12]尹铎皓,范雲鹤,周君华,等.基于傅抱璞模型的岷江上游流域实际蒸散研究[J].中国农村水利水电,2016(2):33-36.

[13]BUDYKO M I.Climate and Life[M].San Diego:Academic Press,1974.

[14]BUDYKO M I.Evaporation under Natural Conditions(English Translation by IPST,Jerusalem)[M].Leningrad:Gidrometeorizdat,1948.

[15]孙福宝.基于Budyko水热耦合平衡假设的流域蒸散发研究[D].北京：清华大学,2007:14-15.

[16]SCHREIBER P.Über die Beziehungen zwischen dem Niederschlag und der Wasserführung der Flüsse in Mitteleuropa[J].Z Meteorol,1904,21(10):441-452.

[17]OL′Dekop E M.On evaporation from the surface of river basins[J].Transactions on Meteorological Observations,1911,4:200.

[18]TURC L.The water balance of soils relation between precipitation,evaporation and flow[J].Annales Agronomiques，1954,5:491-569.

[19]PIKE J G.The estimation of annual run-off from meteorological data in a tropical climate[J].Journal of Hydrology,1964,2(2):116-123.

[20]CHOUDHURY B J.Evaluation of an empirical equation for annual evaporation using field observations and results from a biophysical model[J].Journal of Hydrology,1999,216(1-2):99-110.

[21]ZHANG L,DAWES W R,WALKER G R.Response of mean annual evapotranspiration to vegetation changes at catchment scale[J].Water Resources Research,2001,37(3):701-708.

[22]ALLEN R G,PEREIRA L S,RAES D,et al.Crop evapotranspiration-guidelines for computing crop water requirements-FAO lrrigation and drainage paper 56[J].FAO,Rome,1998,300(9):D05109.

[23]YANG Dawen,SUN Fubao,LIU Zhiyu,et al.Interpreting the complementary relationship in non-humid environments based on the Budyko and Penman hypotheses[J].Geophysical Research Letters,2006,33(18):122-140.

Evapotranspiration Estimation Study Based on Coupled Water-energy Balance Theory in Nenjiang River Basin

LI Hongyan， XUE Lijun， WANG Shijie， AN Fengliang

(College of Environment and Resources, Jilin University, Changchun 130021, China)

As the spatiotemporal variability is large in the regional evapotranspiration, it is difficult to determine through spot monitoring methods. Therefore, the evapotranspiration estimation of river basin is an important but difficult problem in the field of hydrology. The paper starts with Budyko coupled water-energy balance theory, then utilizes Fu′s equation to estimate the actual evapotranspiration yearly in Nenjiang River Basin and typical collection areas. The result shows that Fu′s equation has high precision for estimating evapotranspiration yearly in Nenjiang River Basin, and the estimation result has higher precision in the area with high dryness. Furthermore, the paper analyzes the laws of spatio-temporal evolution of evapotranspiration in Nenjiang River Basin. The results show that there are no trend changes in the actual evapotranspiration and the potential evapotranspiration from 1956 to 2000, and the average annual actual evapotranspiration and potential evapotranspiration from 2000 to 2013 are opposite on the spatial distribution, which the former is decreasing but the later is increasing from upstream to downstream on the whole. Finally, the paper analyzes the distribution rule of underlying surface parameter, which diminishes with the decrease of vegetation coverage from upstream to downstream. The study indicates that Fu′s equation provides a reliable method for evapotranspiration estimation in river basin, which has great significance for forecasting river basin water resources and inquiring into ecological water requirement.

coupled water-energy balance; Budyko formula; Fu Baopu formula; Nenjiang River Basin; evapotranspiration

2016-05-10

国家自然科学基金面上项目(51379088)。

李鸿雁(1968—)，女，内蒙古通辽人，教授，博导，博士，主要从事流域水文循环模拟及水文水资源预测预报方面的研究。 E-mail：lihongyan@jlu.edu.cn。

TV11

A

1002-5634(2016)04-0047-07

(责任编辑：乔翠平)

DOI:10.3969/j.issn.1002-5634.2016.04.008