风电场次同步谐振分析与抑制研究

刘　文，康积涛

(西南交通大学电气工程学院，四川 成都　610031)



风电场次同步谐振分析与抑制研究

刘文，康积涛

(西南交通大学电气工程学院，四川 成都610031)

大规模风电场并网运行，采用串联补偿能够提高输送容量，但是有潜在的引起次同步谐振(subsynchronous oscillation，SSO)的风险。首先构造双馈风电场的模型，采用特征值分析法研究串补度与系统稳定性的关系，并在PSCAD/EMTDC仿真软件上进行验证。为了抑制高串补度引起的感应发电机效应，采用GCSC附加阻尼控制器进行抑制。根据不同抑制效果选择最理想的附加阻尼输入信号。

风电场；次同步谐振；GCSC；附加阻尼控制器

0　前　言

随着能源危机和环境危机的产生，越来越多的清洁能源得到发展，风电场当前也受到相当的重视。由于风能大都集中在远离负荷中心的地方，因而采用远距离输电是不可避免的。当前高压交流输电还是主流的输电方式，为了提高输电能力，常常会采用串联补偿方式，然而含串补的线路有引发次同步谐振的风险[1-2]。

次同步谐振有两种主要的类型：感应发电机效应(induction generator effect,IGE)和轴系扭振(TI)[2]。感应发电机效应是由于输电网络与发电机之间的交互作用，只涉及到系统的电气部分，轴系扭振不仅涉及电气部分还与机械部分有关。由于风轮机轴系的刚度较低，轴系扭振模型频率一般在1～3 Hz，要引起TI需要很高的串补度，因而很少发生。所以在含串补的风电场输电网络中，感应发电机效应是主要的次同步谐振引发因素，主要针对含串补输电网络风电场由感应发电机效应引起的次同步谐振问题。

关于SSO的抑制方法已有大量的研究，包括FACTS装置、励磁、PSS等附加控制[3]，但是大量的研究是针对传统的火力发电系统，对于风电系统的研究则较少。针对风电场感应发电机效应引发的次同步谐振问题，采用FACTS装置进行抑制是经济、有效的方式。由于感应发电机效应主要由系统等值电阻为负造成的，在不影响系统有功输出的情况下，FACTS装置能够很好地调节外部特性，达到抑制SSO的目的。门极可控串联电容器(gate-controlled series capacitor, GCSC)是新型典型串联柔性交流输电装置之一，与其他装置相比，GCSC工作容量较大、控制原理简单、操作错误率低、故障判定准确、反应速度较快，对传统次同步谐振已有较好的抑制能力[4]。

在分析含双馈风电场的次同步谐振的理论基础上，运用仿真软件PSCAD/EMTDC仿真实现感应发电机效应。同时运用GCSC对其进行抑制，由于开

图1　系统模型

环控制达不到理想的效果，将采用附加阻尼控制器增强抑制效果。根据不同附加阻尼输入信号抑制效果不同选择最佳输入信号。

1　系统模型

所采用的模型是基于IEEE第一标准模型演变而来，当风电场中所有风机运行状态相同时，可以用单一风机模型代表整个风电场[5]，则系统模型可用图1表示。该风电场由50台单机容量为2 MW的风电机组组成,发电机的主要参数见参考文献[6]。发电机额定定子电压为0.69 kV，通过出口变压器0.69 kV/35 kV和35 kV/220 kV、220 kV/500 kV升压之后输送到无穷大系统。在500 kV电压等级上加装有串联补偿装置用于提高系统的输送容量。T1、T2、T3表示升压变压器，RL1、RL2表示线路电阻，XL1、XL2表示线路电抗，XC表示串联补偿容抗值。

2　系统状态方程模型

2.1感应发电机模型

感应发电机为d、q坐标系下的四阶模型，状态方程为[7]

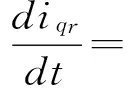
(1)

状态变量与输入变量为

XIG=[ids,iqs,idr,iqr]T

(2)

UIG=[uds,uqs,udr,uqr]T

(3)

式中：is=ids+jiqs、ir=idr+jiqr分别为发电机定子、转子电流;us=uds+juqs、ur=udr+juqr分别为定子、转子电压；Rs、Rr为定子、转子电阻;ωs为角频率标幺值；ωr为转速标幺值；D=ωb/(Lm2-LsLr),ωb为角频率基准值(314 rad/s)。

2.2轴系模型

风电机组低速轴刚性较差，高速轴刚性较高。在轴系模型分析中，将桨叶与低速轴作为一个质量块，而将齿轮箱与高速轴作为完全刚性轴，因而为另一个质量块。轴系系统的状态方程为[8]

(4)

Te=Lm(idsir-iqsidr)

(5)

状态变量与输入变量为

Xshaft=[ωt,ωg,θtg]T

(6)

(7)

式中:ωt、ωg、Ht、Hg、Dt、Dg分别为风轮机和发电机的转速、惯性常数、阻尼系数;Tm、Te分别为风轮机输入机械转矩和发电机的电磁转矩;θtg为两轴系扭转角度;Dtg为轴系阻尼系数;Ktg为轴系刚度系数。

2.3线路和串补模型

将线路电流和串联电容电压作为状态变量，则线路在d、q坐标下的模型为

(8)

状态变量与输入变量为

XTline=[vcq,vcd,iq,id]T

(9)

(10)

式中:vcd、vcq为通过电容电压d、q分量;id、iq为线路电流d、q分量；Ed、Eq为无穷大系统电压d、q分量;XL、XC、RL分别为线路电抗、容抗和电阻。

2.4直流电容模型

背靠背变换器之间的直流电容器用一阶模型表示。

(11)

(12)

(13)

式中:VDC为电容电压，是状态变量;Pr、Pg分别为转子侧和网侧变换器的有功功率。

2.5变流器控制模型

双馈风机控制器分为转子侧控制器(RSC)，如图2所示，与网侧控制器(GSC)，如图3所示[9]。转子侧变换器控制模型通过最大功率跟踪(MPPT)确定发电机的电磁转矩，采用d、q旋转坐标分解，实现双馈发电机输出有功功率和无功功率的解耦控制。网侧控制目标为实现直流电容电压的稳定和发电机端电压的恒定。文献[10]将网侧d轴控制的参考电流设置为0，即网侧只进行了有功的控制。由于这两个控制器含4个PI控制器，故有8个状态变量引入，则总的系统状态矩阵含有20个状态变量。

图2　转子侧(RSC)控制模型

2.6全系统状态方程

整个系统的动态模型已经全部给出，但要构建完整的系统模型还需要几个等量关系。由图1可得电流、电压平衡方程为

Ig=Is+I

(14)

Vg-Vs=jXtgIg

(15)

由式(14)有

图3　网侧(GSC)控制模型

(16)

idg=ids+id

(17)

由式(15)有

vqs=vqg-Xtgidg

(18)

vds=vdg+Xtgiqg

(19)

综合可得到整个20阶系统的状态方程为

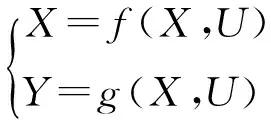
(20)

(21)

3　特征值分析与仿真验证

3.1特征值分析

将式(20)在运行点线性化后为

(22)

由式(22)可得状态方程能用图4表示。

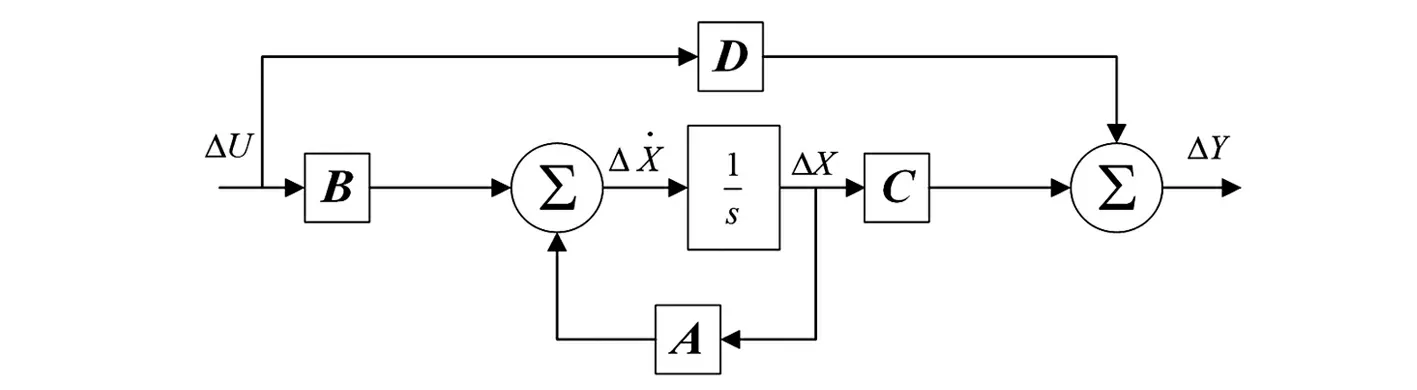
图4　线性化模型框图

根据上述控制流程在Matlab/Simulink中构造系统的模型图，如图5所示。在Matlab/Simulink使用“linmod”函数能够线性化状态方程，并可以方便地计算出状态空间矩阵A、B、C、D，在这里不再赘述。

当风速为9 m/s，串补度为40%时对系统进行小干扰分析，特征值结果如表1。

当风速为9 m/s,串补度依次为90%、80%、70%时的小干扰分析结果如表2。

从表2可以看出，随着串补度的提高，系统也逐渐失稳。且在70%稳定、80%接近临界稳定状态，90%失去稳定。

图5　双馈风电场Matlab状态方程模型

模式特征值模式特征值λ1,2-0.0467±j517.9912λ14-2194.7551λ3,4-0.0668±j312.9624λ15-16.6081λ5,6-0.5041±j102.7480λ16-17.3253λ7,8-0.4115±j1.7858λ17-0.0667λ9,10-0.2115±j0.8992λ18-0.0017λ11,12-4.1394±j43.7326λ190.000λ13-2503.2854λ200.000

表2　不同串补度时特征值

3.2仿真分析

为了进一步验证所分析模型的正确性，下面将在PSCAD/EMTDC仿真软件中对上述模型进行仿真分析。系统开始运行时的风速为9 m/s，串补度为40%，在5 s时将串补度分别提升为90%、80%、70%，观察不同串补度时发电机电磁转矩Te、转速Wpu、发电机端电压Vs的变化情况。波形图如图6～图8所示。

从仿真结果看以看出，串补度为70%时候系统为稳定的，80%时系统相对处于临界稳定状态，90%时候系统发散，说明所分析的模型正确。失稳的原因主要是由于串补度较高时，系统产生了感应发电机效应(IGE)。

图6　串补度为90%时的Te、Wpu、Vs

图7　串补度为80%时的Te、Wpu、Vs

4　GCSC模型与控制结构

GCSC结构如图9所示，由一对反向并联的IGBT和电容器(C)组成。GCSC与TCSC相似，但是在控制支路中没有电抗器。

GCSC控制策略如图10所示，根据期望基波电抗值Xref计算得到初始关断角γ0，由线路电流得到电压相位，计算得到角度α输入门极触发电路，控制IGBT开通与关断。

图8　串补度为70%时的Te、Wpu、Vs

图9　GCSC模型图

图10　GCSC控制图

GCSC的基波等效容抗值为

(23)

式中:XC为电容的容抗值;γ为关断角；δ=(90°-γ)为超前角度。

γ的控制范围为0°～90°，关断角的变化将引起串联电容值的变化，从而导致GCSC基波电抗的变化。当γ为20°时，在PSCAD/EMTDC中进行仿真分析，得到通过GCSC的电流与电压的图形，如图11所示。

5　GCSC抑制次同步谐振研究

GCSC对于同步发电机引发的次同步谐振有抑制效果[4]，为了进一步分析对于风电场的抑制情况，现就GCSC开环控制系统，分析研究系统谐振情况。同样针对图1所示系统，风速为7 m/s，开始串补度为40%，5 s时将串补度提升为70%，期望基波电抗值Xref=0.9XC。

图11　GCSC电压与电流波形图

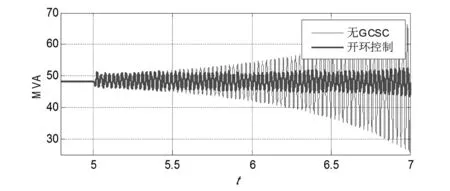
图12　发电机有功变化情况

图13　发电机端电流变化情况

从仿真结果可以看出，开环控制的GCSC并不能完全抑制谐振现象的产生。为了进一步加强GCSC的抑制能力，现在对图 9所示控制策略进行改进，增加附加阻尼控制器，控制框图如14所示。其中ICS(input control signal)为附加阻尼输入控制信号，此信号输入可以选择为发电机转速(Wr)或者线路电流(Iline)。

图14　附加阻尼控制策略

为了比较研究上述两种附加阻尼控制输入信号对谐振抑制情况，现在针对开环模型并增加附加阻尼控制器，仿真分析系统的稳定情况。图15～图17中分别列出发电机有功Pg、定子电流标幺值Is、机端电压标幺值Vs_rms的波形。从仿真结果可以看出，附加阻尼控制器能够很好地抑制谐振的产生和发散，同时可以发现，采用线路电流作为ICS比转速作为输入信号能够更快地抑制次同步谐振。

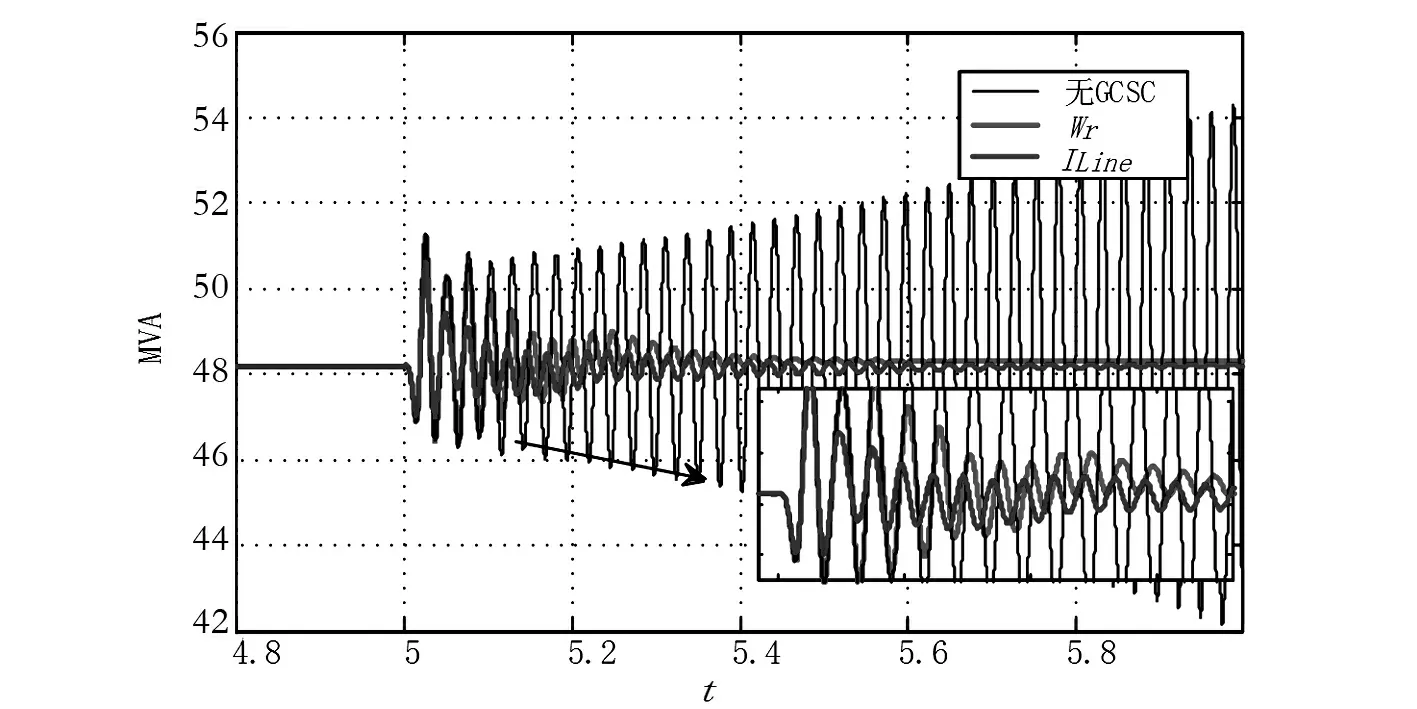
图15　增加附加阻尼控制后Pg变化情况

图16　增加附加阻尼控制后Is变化情况

图17　增加附加阻尼控制后Vs_rms变化情况

6　结　论

根据双馈风电场模型，在Matlab/Simulink中搭建了小干扰模型进行分析，详细分析了串补度与系统稳定性的关系。分析表明，随着串补度的提升，系统越容易失去稳定性。为了验证所分析结论的正确性，在PSCAD/EMTDC上进行了仿真验证。详细介绍了GCSC模型，并在第4、5部分将所构造的模型加入图1系统分析其抑制效果。根据仿真结果可以看出，开环控制不能完全抑制谐振的产生，采用附加阻尼控制器的GCSC系统要更加稳定。对比不同的附加阻尼控制器输入信号发现，采用线路电路作为输入抑制效果更佳。

[1]毕天姝, 孔永乐, 肖仕武, 等. 大规模风电外送中的次同步振荡问题[J]. 电力科学与技术学报, 2012, 27(1): 10-15.

[2]栗然，卢云，刘会兰，等. 双馈风电场经串联并网引起次同步振荡机理分析[J]. 电网技术，2013，37(11)：3073-3079.

[3]汤凡, 刘天琪, 李兴源. 电力系统稳定器及附加励磁阻尼控制器对次同步谐振的影响[J]. 电网技术, 2010, 34(8): 36-40.

[4]任先文，孔详实，王勋，等. 基于GCSC抑制串联输电线路中次同步振荡的研究[J]. 电测与仪表，2012，49(4)：55-58.

[5]董晓亮，谢小荣，杨煜，等. 双馈风机串补输电系统次同步谐振影响因素及稳定区域分析[J]. 电网技术，2015，39(1)：189-193.

[6]王波.含双馈机组风电场次同步振荡分析与抑制[D]. 重庆：重庆大学，2013：29-30.

[7]Lihui Yang, Zhao Xu, Jacob Stergard, et al. Oscillatory Stability and Eigenvalue Sensitivity Analysis of a DFIG Wind Turbine System[J]. IEEE Transactions on Energy Conversion, 2011, 26(1): 328-339.

[8]顾威，徐梅梅，邵梦桥，等. 大规模风电场次同步振荡分析[J]. 2015, 36(4):95-103.

[9]Lingling F, Kavasseri R, Zhixin L M. Modeling of DFIG-based Wind Farms for SSR Analysis[J]. IEEE Trans. on Power Delivery, 2010, 25(4): 2073-2083.

[10]Feng Wu, Xiao-Ping Zhang, Keith Godfred, et al.

Modeling and Control of Wind Turbine with Doubly Fed Induction Generator[C]. Power Systems Conference and Exposition, 2006:1404-1409.

刘文(1990)，硕士研究生，研究方向为新能源发电与并网;

康积涛(1962)，硕士生导师，研究方向为电力系统无功与电压稳定性、电力系统次同步振荡。

When large-scale wind farms in parallel operation with power system, the transmission capacity can be improved by using series compensation, but it may lead to risks which causes subsynchronous oscillation (SSO). Firstly, the model of wind farms with doubly-fed induction generators is constructed, the modal analysis is performed to study the relationship between system stability and series compensated degree, and the conclusion is verified by PSCAD/EMTDC simulation software. In order to prevent induction generator effect caused by the high series compensated degree, gate-controlled series capacitor (GCSC) with additional damping controller is adopted. According to the different inhibition effect, the most ideal additional damping input signal is selected.

wind farm; subsynchronous oscillation (SSO); gate-controlled series capacitor (GCSC); SSR damping controller (SSRDC)

TM614

A

1003-6954(2016)03-0026-06

2016-01-15)