不同风电机组接入电网的暂态电压稳定性研究

李自明，常喜强，王海云，姚秀萍

(1.新疆大学，新疆 乌鲁木齐　830008；2.新疆电力调度控制中心,新疆 乌鲁木齐　830001)



不同风电机组接入电网的暂态电压稳定性研究

李自明1，常喜强2，王海云1，姚秀萍2

(1.新疆大学，新疆 乌鲁木齐830008；2.新疆电力调度控制中心,新疆 乌鲁木齐830001)

在中国，因为特殊的地理环境，风电装机容量在整个电网中的占有率得到激增，风电场一般建设在电力系统输电网的末端，且地区经济不发达，网架结构较弱。但风电的快速发展，使得在短时间内大规模风电场集中接入电网，给电网的有功和无功平衡带来大幅度波动，这种大的扰动严重威胁到电网的暂态电压稳定。因此建立了基于普通异步风力发电机组(AWT)、双馈异步风力发电机组(DFIG)的暂态数学模型，并以新疆北部某一地区作为算例仿真分析了这两种风力发电机组以不同比例接入系统后的暂态电压稳定性。根据仿真得出的临界故障清除时间(CCT)表明，双馈风力发电机组接入系统时的暂态电压比普通异步风力发电机组接入系统更稳定。

风电并网；普通异步风力发电机组；双馈异步风力发电机组；暂态电压稳定；极限切除时间

截止2014年年末，新疆电网电源规模整体继续呈现快速增长态势，新能源中的风电增长仍占主导地位，且增速加快。新疆电网新增电源明细情况表如表1所示。

表1　新疆电网新增电源明细

从表1可看出，2014年新疆电网新增风电场42座，新增风电装机容量为5 155 MW，占新疆电网各类电源新增装机总容量的26.3%，同比增长78.9%，增速远超火电(35.8%)、光伏(41.3%)。风电机组装机容量增加，风电并网规模也随之增长，风能现已逐步替代常规能源并成为中国电网中的重要电源之一。由于风能具有间歇性、不可调度性的特点，这使得大规模风功率注入系统后，会改变电网无功潮流以及系统电压，特别是那些风电场穿透功率较大的电网，一旦发生故障，将会造成大量风机脱网，威胁电力系统的安全运行[1]。现阶段中国风电场中普通异步风电机组还占有相当大的比重，这种风电机组在运行过程中需要向系统吸收无功功率，将会对电力系统的电压稳定性产生巨大影响[2]。因此，针对风电场中不同风电机组以不同比例接入系统后的暂态电压稳定性问题进行深入的研究。

系统的暂态电压稳定性是指发生扰动的电力系统不会出现电压持续降低或者解列的能力[3]。若电压严重降低会导致电动机停转，发电机负荷降为0，系统振荡直至崩溃，同时电压过低也会导致STATCOM等无功电源的出力降低，进而降低了系统的电压稳定性。文献[4-6]通过在Matlab中搭建风电场并网系统模型，分析了在网侧发生三相短路时的暂态电压稳定性。文献[7-9]通过仿真分析了双馈风电机组接入地区电网的电压稳定，得出双馈风电机组在故障后能够减少系统所需的无功储备，从而有利于地区电网的电压稳定。

针对上述多数文献仅对单种风机并网进行研究，但是很少有对不同风机组成的风电场并网暂态电压稳定性进行研究问题，下面建立了基于普通异步风电机组和双馈风电机组的暂态模型。以新疆北部某一地区为案例仿真分析了不同风电机组，按不同比例组成的风电场接入某一地区电网后系统的暂态电压稳定性。根据仿真结果，可以得出双馈风力发电机组接入系统的暂态电压比普通异步风力发电机组接入系统更稳定。

1　数学模型

1.1普通异步风电机组暂态模型

随着新型风力发电机组性价比的提升以及新电网导则的引入，普通异步风力发电机最终退出风电领域已是大势所趋；但就目前电网而言，这类风电机组在电网还占有相当比重，仍然要对其模型进行深入研究。普通异步风力发电机组一般是由叶片、轮毂、齿轮箱、轴系以及异步发电机几部分组成。它的能量流动如图1所示。

图1　普通异步风电机组的能量流动

图1中的普通异步风电机组首先由叶片扑获风能，然后将风能转换为作用在轮毂上的机械能，由此带动齿轮箱和轴系的转动，再将此机械能转换为发电机上的电能，电能向电网传输过程通常需要并联电容器，来补偿电力系统感性负荷的无功功率，改善电能质量，最终将优质电能输送至电网的受端。其中风能与机械能的转换是形成电能的关键部分。风能与风机的机械转矩之间的关系可用式(1)表示[10]。

(1)

式中：Mw为风力机叶片转矩；ρ为空气密度；R为叶片半径；Vw为作用于叶片的风速;λ=ΩR/Vw为叶尖速比，Ω=2πR/60，为叶片机械角速度；ΩN为风力机额定机械角速度；PN为风力机额定功率；CP为风能利用系数，其大小与叶尖速比λ和叶片桨距角β有关。

研究风电系统的暂态特性需要考虑异步发电机的机电暂态过程，普通异步风力发电机等效电路如图2所示。

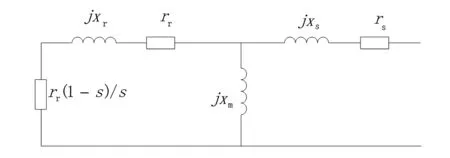
图2　异步电机等效电路

异步发电机的定子电压方程为

Vs=-(rs-jX′)Is+E′

(2)

式中:E′、Vs、Is、rs分别为发电机暂态电势、定子电压、输出电流和定子电阻；X′=Xs+XrXm/(Xr+Xm)为发电机等效暂态电抗，Xs、Xr和Xm分别为发电机定子电抗、转子电抗和激磁电抗。

异步发电机转子电磁暂态方程[18]为

(3)

式中：s为滑差；xs和xm分别为发电机定子电抗和激磁电抗。x′=xs+xrxm/(xr+xm)，为发电机等效暂态电抗；f0为系统频率,Hz。

1.2DFIG风电机组暂态模型

基于DFIG的双馈风力发电机是目前风电场采用的主流机型之一，它是一种采用脉宽调制技术的新型风力发电机组，该类型的风力发电机的定子绕组与电网有电气联接，其转子绕组也通过变频器(一般由转子侧整流器、控制器、直流电容及网侧逆变器组成)与电网相联，如图3所示。

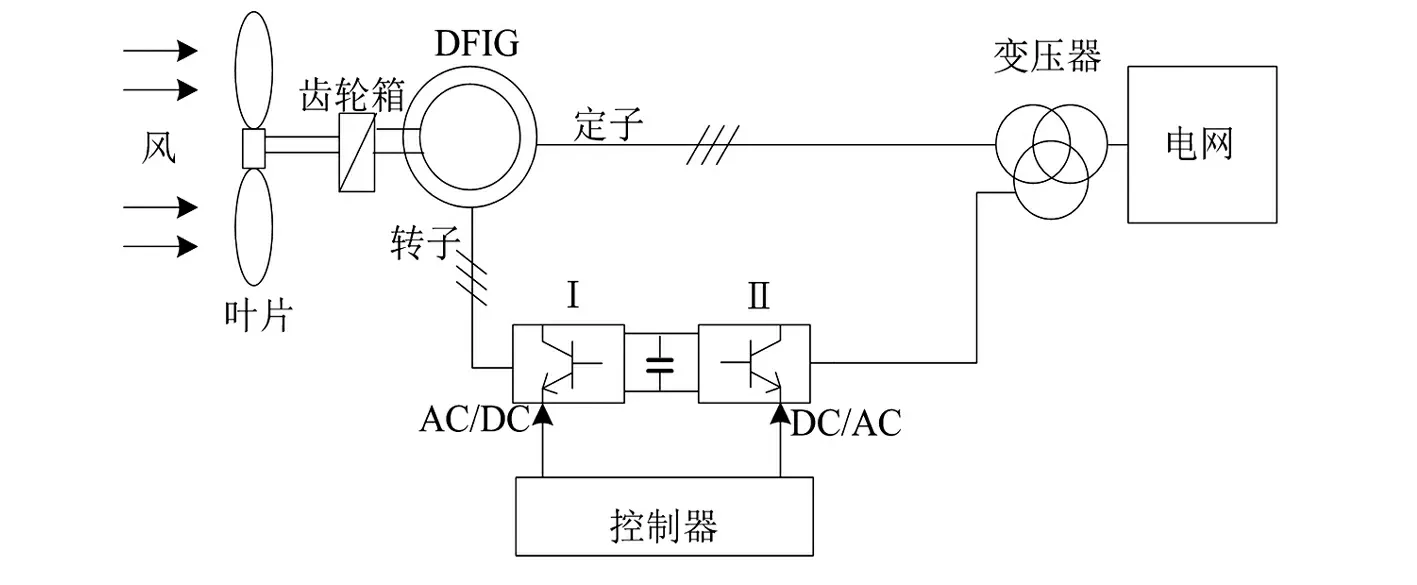
图3　双馈风电机组简图

图3所示的双馈风电机组的转子绕组由变频器和控制器提供幅值、相位可调的励磁电源，供给三相低频励磁电流，以实现恒频输出。若叶片扑获的风速较低，则风力发电机必须运行在低于同步转速的状态才能有较高的发电效率。为达到发电机机械转矩与电磁转矩两者平衡，转子绕组从电网吸收一定数量的功率再通过定子绕组送回电网，以保持电网的功率平衡。若叶片扑获的风速较高，风力发电机则需要运行在高于同步转速的状态才能发出更多有功；在这种情况下一部分功率将直接通过转子绕组送入电网；当风力发电机运行在同步速时，如果忽略损耗，转子绕组通过的功率都由定子绕组完成。

图3中的双馈风力发电机的转子回路可以通过发电机滑环外接电压源，即转子电压urd与urq不等于0，并且通过控制转子外接电压的值可以控制双馈感应发电机发出的有功与无功功率。由贝兹理论可知，风机的输出机械转矩为

Tm=Pm/ωt=0.5ρπR2CpVm3/ωt

(4)

式中：Pm为风机的输出电磁功率；CP为风机的风能利用系数；ρ为空气密度；R为风轮机叶片半径；Vm为风速。

风能利用系数CP可按式(5)计算得

Cp=0.44(125/λi-6.94)e-16.5/λi

(5)

式中：λi=1/(1/λ+0.002)；λ为叶尖速比，其定义为λ=ωtR/Vm。

图3中的变频器采用的是可以双向流动的交-直-交变频装置，这是为了适应双馈风力发电机转子超同步时向系统馈送功率或是次同步时从系统吸收功率的需要。如图4(a)、(b)所示，给出了d、q轴下的DFIG的等效电路。

图4　DFIG的d、q轴等效电路图

电磁转矩为

(6)

式中：ids和iqs分别为图4中定子电流的d、q轴分量；idr和iqr分别为图4中转子电流的d、q轴分量；Lm为定转子间互感；ω0、ω、ωs分别为电机同步角速度、转子角速度和转差角速度；Te为风力发电机电磁转矩；J为发电机转动惯量；Np为极对数；S为转差率。

2　案例仿真分析

风电场内输电线路(架空线或者地埋电缆线)发生短路故障，会造成故障点附近电网的电压水平降低，电容器、SVC等无功电源的出力降低，使得某些线路或变压器过载，导致线路上的无功损失大幅增加；如果故障致使发电机组退出运行，除了造成电网有功缺失外，也会造成电网无功电源的损失。上述现象都会引起系统的暂态电压问题[11-12]。

而新疆地区的风电资源主要集中在东疆和北疆片区。由于北疆电网220 kV布点多、网架密；且该地区感性无功补偿容量不足，冬季小负荷期间该地区部分末端厂站电压偏高运行较难控制。尤其是在大量风电集中投产后，由于短路水平较低，风电场SVC难以协调控制，导致该地区的风电场升压站特别是布尔津、龙湾、额尔齐斯汇集站电压受风电出力影响波动较大，易出现低频振荡问题。故以新疆北部某一地区电网为例，将不同风电机组以各种比例组合来分析系统暂态电压稳定性。该地区主要网架结构如图5所示。该地区西部风资源丰富，规划建设的6大风电场，总装机容量为346.5 MW。已经建设0.75×66 MW的布尔津天润风电场，机组采用750 kW普通异步风电机组和1.5 MW双馈风电机组，风电机组出口电压为0.69 kV，通过箱式变电站升压至10 kV，送至风电场升压站升至110 kV，再通过110 kV线路接入金风风电T变电站。

由图5可以看出，该地区电网通过220 kV的克额线(克拉玛依—额尔齐斯)、丰龙线(和丰—龙湾)与新疆主网联系，该地区主网架结构采用110 kV电压等级。刚建成的龙湾变电站是几个风电场和冲乎尔水电站汇流的地方，且通过220 kV线路直接与额尔齐斯变电站相连，地理位置极其重要；布尔津变电站靠近几个常规电厂，与新疆主网连接的额尔齐斯以及龙湾变电站连接了大量负荷，基于以上考虑，主要分析这几个重要变电站的暂态电压稳定性。布尔津天润风电场所接入的风电机组参数如表2所示。

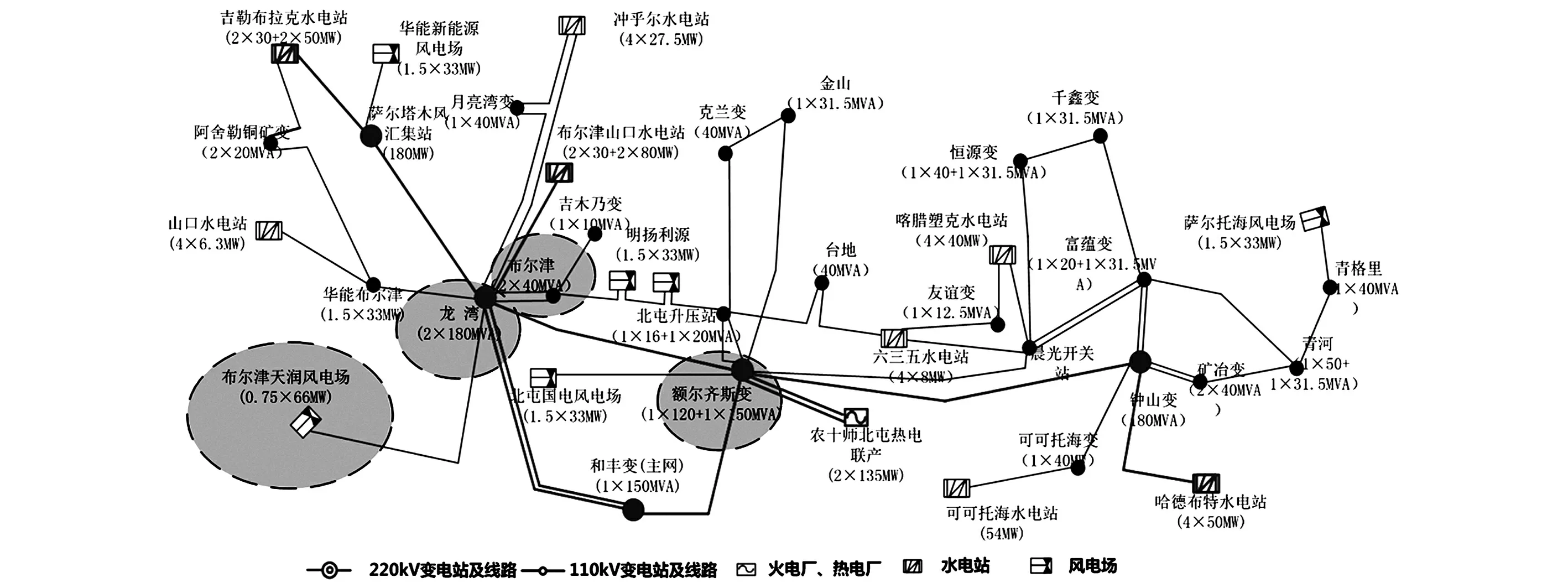
图5　新疆北部某地区网架结构示意图

普通异步风电机组发电机参数风力机参数双馈风电机组发电机参数风力机参数额定功率/MW0.75切入风速Vi/(m·s-1)3额定功率/MW1.5切入风速Vi/(m·s-1)3额定电压/V690基本风速Vr/(m·s-1)15额定电压/V690基本风速Vr/(m·s-1)11.8额定频率/Hz50切除风速V0/(m·s-1)25额定频率/Hz50切除风速V0/(m·s-1)25定子电阻R1/(p.u.)0.0038风轮半径/m30定子电阻R1/(p.u.)0.0064风轮半径/m35.2定子电抗L1/(p.u.)0.1248塔高/m70定子电抗L1/(p.u.)0.1421塔高/m80转子电阻R2/(p.u.)0.0083推力系数CT0.2转子电阻R2/(p.u.)0.0091推力系数CT0.2转子电抗L2/(p.u.)0.1791传动轴系数(双质块)时间系数/s5.24转子电抗L2/(p.u.)0.1920传动轴系数(双质块)时间系数/s7.64激磁电抗Lm/(p.u.)6.77激磁电抗Lm./(p.u.)7.02转子惯性时间常数Tj3.04转子惯性时间常数Tj1.54定子开路转子时间常数T'd01.44定子开路转子时间常数T'd01.14

该地区电网在最大负荷方式下运行，风电场接入点PCC处在t=2 s发生三相短路故障，故障在t=2.57 s清除。通过仿真风电机组各种比例组合，发现以下几种不同风电机组组合方式具有代表性，所以就以下几种情况来分析系统暂态电压稳定：

算例1：100%普通异步风电机组的天润风电场接入系统；

算例2：70%普通异步+30%双馈风电机组的天润风电场接入系统；

算例3：50%普通异步+50%双馈风电机组的天润风电场接入系统；

算例4：30%普通异步+70%双馈风电机组的天润风电场接入系统；

算例5：100%双馈风电机组的天润风电场接入系统。仿真结果如图6所示。

表3　极限切除时间表

从图6(a)～图6(d)可以看出，在t=2 s天润风电场接入点PCC处发生三相短路故障，故障在t=2.57 s清除的情况下，由100%普通异步感应发电机组成的天润风电场接入系统后暂态电压失去稳定；而随着双馈风电机组的增加，系统暂态电压稳定性变好，当全部由双馈风力发电机组构成时，系统暂态电压稳定性是最好的，故障清除后系统能够保持

图6　系统电压曲线

稳定。这是由于普通异步感应发电机没有像DFIG所具有的换流器控制环节，当系统发生短路故障时，机端电压跌落，转子加速；同时普通异步感应发电机从电网吸收大量的无功功率来保持高转速，这将导致电压进一步跌落，如不及时采取相应的补偿措施，当接入的系统较弱时，最终会失去稳定。而双馈风力发电机组具有换流器控制环节，在系统短路故障时，可以提供一定的无功支持，使系统电压得以恢复或者过渡到一个新的稳定点。从图6(b)～图6(d)可以看出连接常规能源(水电站)的龙湾变电站和布尔津变电站比连接大量负荷的额尔齐斯变电站的暂态电压稳定性好。

同时，不同风电机组对系统故障CCT也不同。从表3可以看出，算例5的CCT最大，算例1的极限切除时间最小，即双馈风力发电机组风电场接入系统暂态电压较普通异步风力发电机组风电场更稳定，与从图6电压仿真曲线得出的结果一致。

3　结　论

基于不同风电机组组合方式接入天润风电场对暂态电压进行时域仿真，由仿真结果给出了不同风力发电机组的风电场对系统暂态电压不同程度的影响。

1)电网发生三相短路故障将引起周围节点电压降低,当故障出现在风电场周围地区时，风电场吸收的无功增加，若该区域无功不充裕，则风电机组的机端电压会持续降低,甚至崩溃，进而会引起风电场并网节点及其周围节点的电压出现较严重的暂态电压失稳的现象，影响电网的安全运行。

2)当不同风力发电技术的风电场接入系统，离常规电源近的地区，其暂态电压越稳定；反之，负荷比较集中的地区，无功需求大，暂态电压稳定性差。

3)装有双馈风电机组的风电场比普通异步风电机组的风电场需要的无功功率小，甚至不需要，所以其暂态电压也更稳定，对电压的调节也更好，有利于地区电网的电压稳定性。

[1]刘彦呈, 王川, 魏一. 电力系统大扰动下暂态电压稳定的动态特征分析[J]. 电力系统保护与控制, 2011, 39(10): 11-17.

[2]付小伟. 风电场的接入对电力系统电压稳定性的影响研究[D]. 长沙: 长沙理工大学, 2013.

[3]张建华, 王健, 陈星莺, 等. 双馈风机低电压穿越控制策略的分析与研究[J]. 电力系统保护与控制, 2011,39(21): 28-33.

[4]谢维. 直驱型永磁风电机组并网控制系统的研究[J]. 电源技术, 2014, 38(10): 1907-1909.

[5]肖园园, 李欣然, 张元胜, 等. 直驱永磁同步风力发电机的等效建模[J]. 电力系统及其自动化学报, 2013，25(1): 12-17.

[6]张会参, 秦艳辉. 基于SVC的异步风力发电机并网系统的暂态稳定性研究[J]. 电工电气, 2011(2): 4-7.

[7]宋伟伟, 李强, 袁越. 双馈风电机组接入地区电网后的电压稳定性分析[J]. 电网与清洁能源, 2009, 25(5): 36-40.

[8]田新首, 王伟胜, 迟永宁, 等. 双馈风电机组故障行为及对电力系统暂态稳定性的影响[J]. 电力系统自动化, 2015, 39(10): 16-21.

[9]李东东, 王凯凯, 叶辰升. 采用双馈机组的风电场无功功率控制研究[J]. 电力系统保护与控制, 2013, 41(13): 37-42.

[10]王纯琦, 吐尔逊·依布拉音, 晁勤. 基于 Matlab的含风电电网建模与仿真[J]. 可再生能源, 2006(5): 61-64.

[11]卢锦玲, 石少通, 徐超, 等. 含大型风电场系统暂态电压稳定性分析[J]. 华北电力大学学报, 2014, 41(1): 45-52.

[12]马敏. 风电接入对电网暂态稳定性及调峰能力的影响研究[D]. 北京: 华北电力大学, 2010: 19-22.

李自明(1989)，硕士研究生，主要研究方向为电力系统及其自动化；

常喜强(1976)，高级工程师，主要研究方向为电力系统分析与控制；

王海云(1973)，教授、硕士研究生导师，主要研究方向为可再生能源发电与并网技术；

姚秀萍(1961)，客座教授、硕士生导师、高级工程师，主要研究方向为电网调度运行、继电保护。

In China, the installed capacity of wind power in the whole power grid is increasing due to the special geographical environment. The construction of wind farms is generally located in the transmission end of power system, the regional economy is not developed and the grid structure is weak. But with the rapid development of wind power, the large-scale wind farms in a short period of time are concentrated in power grid, which makes a drastic fluctuation for the balance of active power and reactive power in power grid and makes a serious threat to the transient voltage stability of power grid. The transient mathematical models based on common asynchronous wind turbine (AWT) and doubly-fed inductiongenerator (DFIG) are established, and taking the simulation of a certain area in the north of Xinjiang for example, the transient voltage stability of these two kinds of wind power generator units are analyzed. The critical clearing time (CCT) obtained from the simulation shows that the transient voltage of DFIG is more stable than that of AWT when they are integrated with power grid.

wind power integration; asynchronous wind turbine (AWT); doubly-fed induction generator (DFIG); transient voltage stability; critical clearing time (CCT)

TM712

A

1003-6954(2016)03-0021-05

2016-01-19)