认知中继选择系统发射功率受限时的性能研究*
2016-08-25姬士龙王利红
姬士龙, 郭 辉, 王利红
(河南理工大学 计算机科学与技术学院,河南 焦作 454000)
认知中继选择系统发射功率受限时的性能研究*
姬士龙, 郭辉, 王利红
(河南理工大学 计算机科学与技术学院,河南 焦作 454000)
基于译码转发协议,对一个双跳认知中继选择系统的中断性能进行了研究。该系统采用半双工的通信模式,所有节点均配置单个天线,次级系统同时受到来自于主接收用户最大干扰功率和最大传输功率的双重限制。在独立非同一分布的瑞利信道环境下,推导出了中断概率的准确闭合表达式和高传输功率时的渐进闭合表达式,并利用蒙特卡罗仿真实验对理论分析结果的正确性进行了验证。实验结果表明:中继个数的增加降低了中断概率,提升了系统的性能,但是提升空间有限。另外,最大干扰门限和最大传输功率的变化关系给系统性能的提升带来瓶颈。
认知协作通信; 译码转发; 瑞利衰落; 最大传输功率; 干扰限制
0 引 言
协作通信技术作为一种新的空间分集技术的出现,使未来无线系统的高数据覆盖传输成为可能。它能够很好地应对多径衰落对信号传输产生的有害影响和降低系统的中断概率,并且可以扩大信息传输的覆盖范围。最近,认知无线电网络引起了业界和学术界的广泛关注[1~3],它能够显著地提高频谱的利用效率。在认知无线电网络中定义了两个群体:主用户和次级用户。其中,主用户被授予了一定的频带,次级用户可以感知到主用户空闲的频带(即所谓的频谱漏洞),并在不对主用接收用户造成任何有害干扰的情况下共享主用户空闲的频带进行通信,这样极大地提高了频谱的利用率[4]。
近年来,协作分集被运用到认知无线电网络中,形成了协作频谱共享无线电网络,许多的研究者对其进行了广泛的研究。考虑主用户的最大干扰限制,文献[5]对认知无线电网络中相关的中继选择算法进行了研究。文献[6]研究了基于完全信道信息和部分信道信息的最佳中继选择策略认知中继网络的中断概率,推导了这两种策略中断概率的封闭表达式。针对认知无线电网络传输速率不足及对主用户造成干扰等问题,文献[7]提出一种能够满足认知用户对主用户干扰限制要求的中继选择算法,提高了系统吞吐量。考虑所有的中继节点都参与通信的情况下,文献[8]提出了一种最优的功率分配算法。文献[9]采用放大转发(amplify-and-forward,AF)协议,在瑞利衰落环境下研究了偏中继选择系统的中断性能。基于多路发送协作,文献[10]研究了DF系统的中断性能。最近,文献[11]基于一种最佳中继选择策略,在瑞利衰落环境下采用AF协议对中继选择系统的性能进行了研究,推导出了中断概率的近似闭合表达式。同时,针对DF协议,文献[12]在韦伯衰落信道中对最佳中继选择系统进行了研究。然而,文献[11,12]都忽略了次级系统最大发射功率对整个系统的影响。
基于上文的分析,本文在频谱共享环境下,考虑一个同时受主用户干扰门限和最大发射功率双重限制的中继选择系统,对该系统的性能进行了研究。并在独立非同一分布的瑞利衰落信道中推导出了中断概率的准确闭合表达式,同时,为了对系统性能作进一步的研究,推导出了中断概率的渐进闭合表达式。基于得到的表达式,对系统的性能进行了研究。
1 系统和信道模型
如图1所示,考虑一个双跳的认知无线电网络,该系统包括一个信源S,K个DF中继Rk(k=1,2,…,K),一个信宿D和一个主用户接收机PR。所有的终端均采用半双工模式,并且使用单天线。图中,hS,P,hS,k,hk,P,hk,D(k=1,2,…,K)分别表示S到PR,S到Rk,Rk到PR,Rk到D的信道系数。
次级用户通信系统占用2个时隙:第一个时隙内,信源S以发射功率PS向信宿D和K个中继发送信号。第二个时隙内,中继Rk对信源S发送过来的信号进行解码,然后重新编码后以发射功率Pk将编码后的信号发送给信宿D。为了不对主网络产生干扰,信源S和中继Rk的发射功率必须满足:PS|hS,P|2≤Q,Pk|hk,P|2≤Q,其中,|·|表示绝对值,Q表示为PR所能忍受的最大干扰功率(最大干扰门限)。同时,也要受到次级系统最大发射功率Pm的限制。那么,信源S和中继Rk的发射功率分别表示为
(1)
(2)
则第k条链路的第一跳(S→Rk)和第二跳(Rk→D)的接收信噪比分别可以表示为
(3)
(4)
式中N0为加性高斯白噪声的功率。此时,第k条中继链路的信噪比可表示为
γk=min(U1k,U2k)
(5)
本文假设所有的链路都服从独立而不同分布的瑞利衰落,因此,信道增益|hS,P|2,|hS,k|2,|hk,P|2,|hk,D|2服从功率均值分别为ΩS,P,ΩS,k,Ωk,P,Ωk,D的指数分布。这样,在信宿D处系统的端到端瞬时信噪比可以表示为
(6)
2 中断性能分析
2.1准确分析
中断概率OP通常被定义为:次级用户接收机D处的瞬时信噪比γD低于预设定的门限值γth时的概率。因此,该系统的中断概率可以表示为
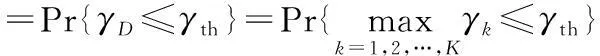
(7)
式中Pr{·}为概率,Fγk(·)为γk的累积分布函数。
由式(3)和式(4)可知,U1k和U2k相互独立,则γk的累积分布函数为
Fγk(γ)=Pr(min(U1k,U2k)<γ)
=1-Pr(U1k>γ)Pr(U2k>γ)
=FU1k(γ)+FU2k(γ)-FU1k(γ)FU2k(γ)
(8)
下面分别求解FU1k(·)和FU2k(·)的闭合表达式
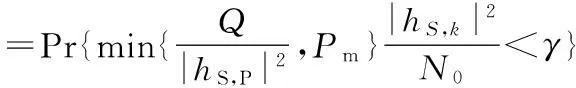
(9)
由于X∈{|hS,P|2,|hS,k|2,|hk,D|2,|hk,P|2}服从参数为Ω∈{ΩS,P,ΩS,k,Ωk,D,Ωk,P}的瑞利分布,故其概率密度函数和累积分布函数可以分别表示为
(10)
(11)
式中exp(·)为以e为底的指数函数。 将式(10)和式(11)代入式(9),可以计算得到的U1k的累积分布函数为

(12)
同理,可以求得U2k的累积分布函数为
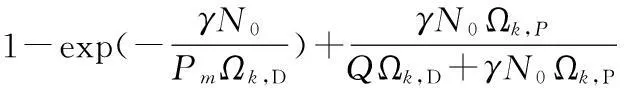
(13)
因此,将式(8)、式(12)和式(13)代入式(7)便可得到中断概率的准确闭合表达式
Pout=
(14)
2.2渐进分析
下面来讨论系统在高信噪比时(Pm→∞)中断概率的渐进表达式。此时由式(1)和式(2)可知,信源S和中继Rk的发射功率将完全由Q,hS,P和hk,P确定。经过计算可得,当Pm→∞时,式(12)和式(13)的累积分布函数的渐进表达式可分别表示如下
(15)
(16)
将式(8)、式(15)和式(16)代入式(7),可以得到渐进分析下中断概率的表达式为
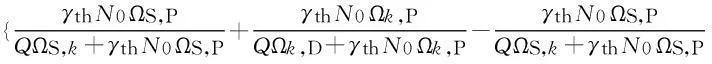
(17)
实际上,中断概率在Pm→∞时的渐进结果即表示了“中断地板效应”中地板值的大小。
3 数值仿真与分析
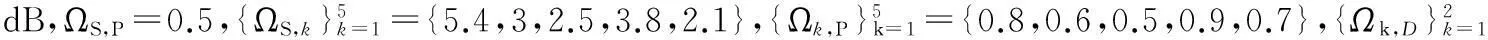

图2 中断概率与中继个数的关系Fig 2 Relationship between break off probability and numbers of relay
在图3中,本文绘出了中断概率与主用户干扰门限的关系曲线来研究干扰门限对系统中断概率的影响。图中曲线显示,当主用户放宽对次级用户的限制,中断概率降低,系统性能得到改善,当次级系统的最大发射功率增加到大于等于主用户干扰门限值的时候,主用户的干扰门限成为决定性因素,从而导致了“中断地板效应”的出现。另外,在图3中给出了无干扰限制(即:主用户能承受的干扰无限大)时中断概率的变化曲线。通过比较可以发现,当主用户对次级用户的通信不产生任何限制的情况下,系统的性能是无比优越的,“中断地板”也不会出现。在图4中,以(Q/N0)的变化为横坐标来研究中断概率与次级用户最大发射功率的关系。图中可以看到,次级用户最大发射功率的增加带来了系统性能的提升,由于对于固定的发射功率,当主用户干扰门限值增加到大于等于最大发射功率值的时候,次级系统的发射功率起主导作用,所以,“中断地板效应”依然会出现。然而,当发射功率趋于无穷大的时候,“中断地板”消失,系统则呈现出优越的性能。
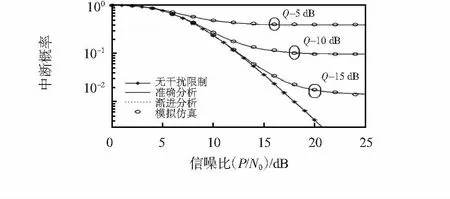
图3 中断概率与主用户干扰门限的关系Fig 3 Relationship between break off probability and interference threshold of primary user
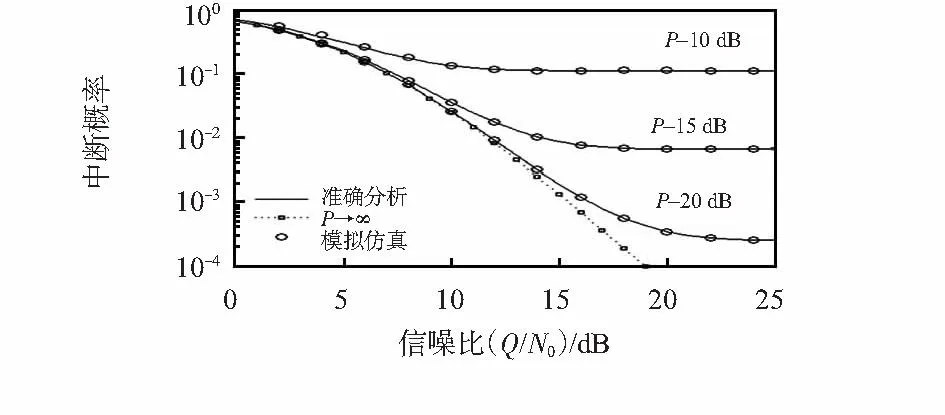
图4 中断概率与最大传输功率的关系Fig 4 Relationship between break off probability and the maximum transmission power
4 结束语
本文在瑞利衰落环境下,对一个基于译码转发中继选择系统的性能进行了研究。考虑次级通信系统受到来自主用户干扰门限和最大发射功率的双重限制的情况下,推导出了在准确分析和渐进分析下中断概率的闭合表达式;同时利用计算机模拟仿真验证了分析结果的正确性。实验结果表明:中继个数的增加带来了系统性能的提升,但提升空间有限;另外,主用户的干扰门限和最大发射功率的变化关系在某种程度上导致了“中断地板效应”的出现,使系统性能的改善出现了瓶颈。
[1]Wei Li,Cheng X,Jing T,et al.Spectrum assignment and sharing for delay minimization in multi-hop multi-flow CRNS[J].IEEE J Sel Areas Commun:Special Issue on Cognitive Radio,2013,31(11):2483-2493.
[2]Xing X,Jing T,Huo Y,et al.Channel quality prediction based on Bayesian inference in cognitive radio networks[C]∥Proc IEEE INFOCOM,2013:1465-1473.
[3]Yoon S,Li E L,Liew S C,et al.Quick sense:Fast and energy-efficient channel sensing for dynamic spectrum access networks[C]∥Proc IEEE INFOCOM,2013:2247-2255.
[4]Song M,Xin C,Zhao Y,et al.Dynamic spectrum access:From cognitive radio to network radio[J].IEEE Wireless Commun,2012,19(1):23-29.
[5]Zou Y,Zhu J,Zheng B,et al.An adaptive cooperation diversity scheme with best-relay selection in cognitive radio networks[J].IEEE Transactions on Signal Processing,2010,58(10):5438-5445.
[6]嵇建波,葛仁华,孙山林.认知无线电选择中继放大转发协议性能分析[J].电讯技术,2013,53(3):279- 283.
[7]喻莉,陈海波,刘聪,等.基于位置和干扰限制的认知中继选择算法[J].计算机工程,2012,38(4):7-9.
[8]Francesconi D,Van Hecke J,Giannetti F,et al.Distributed dynamic resource allocation for cooperative cognitive radio[C]∥2012 IEEE Wireless Communications and Networking Conference(WCNC),2012:679-683.
[9]Lee I H.Outage performance of efficient partial relay selection in amplify-and-forward relaying systems over rayleigh fading channels[J].IEEE Commun Lett,2012,16(10):1644-1647.
[10] Lee I H,Lee H,Choi H H. Exact outage probability of relay selection in decode-and-forward based cooperative multicast system-s[J].IEEE Commun Lett,2013,17(3):483-486.
[11] Bao V N Q,Duong T,da Costa D B,et al.Cognitive amplify-and-forward relaying with best relay selection in non-identical Rayleigh fading[J].IEEE Commun Lett,2013,17(3):475-478.
[12] Samarasekera A C J,Dac-Binh H,Huu K N.Best relay selection for underlay cognitive relaying networks over Weibull fading channels[C]∥2014 International Conference on Computing,Management and Telecommunications(ComManTel),2014:7-12.
姬士龙(1987 -),男,河南信阳人,硕士研究生,研究方向为协作通信。
Research on property of cognitive relay selection system with transmission power constraint*
JI Shi-long, GUO Hui, WANG Li-hong
(School of Computer Science and Technology,Henan Polytechnic University,Jiaozuo 454000,China)
Break off performance of a dual-hop cognitive relay selection system is researched based on decode-and-forward(DF)protocol.The system uses half-duplex communication mode and all nodes are equipped with single antenna.Also,both the maximum interference power from primary receiver and the maximum transmission power constraint secondary system.Moreover,both the exact closed-form expression for break off probability and high transmission power asymptotic closed-form expressions are derived in non-identical Rayleigh fading channel environments.The correctness of theoretical analysis result is verified via Monte-Carlo simulations.Experimental results show that break off probability is reduced and the system performance is improved as numbers of relays increase,but improvement is limited.Moreover,changing relationship between the maximum interference threshold and the maximum transmission power brings bottleneck to improvement of system.
cognitive cooperative communications; decode-and-forward;Rayleigh fading; the maximum transmission power; interference constraint
2015—11—05
河南省教育厅科学技术研究重点项目(12B510011,12A520022);河南理工大学博士基金资助项目(B2013—036,B2009—21)
TN 929.5
A
1000—9787(2016)08—0063—04
DOI:10.13873/J.1000—9787(2016)08—0063—04
