车辆路径选择对交通流分布的影响
2016-08-25李邦兰周代平
彭 勇,李邦兰,周代平
(1.重庆交通大学 交通运输学院,重庆 400074;2.深圳市新城市规划建筑设计有限公司,广东 深圳 518000)
车辆路径选择对交通流分布的影响
彭勇1,李邦兰1,周代平2
(1.重庆交通大学交通运输学院,重庆400074;2.深圳市新城市规划建筑设计有限公司,广东深圳518000)
在无诱导信息条件下,驾驶员通常依靠近期经验选择出行路径。在行为强化理论基础上,建立了基于有限理性模糊博弈的无诱导信息车辆路径选择模型,得出了不同初始状态下的博弈平衡结果。数值仿真结果表明:在无诱导信息条件下,路网的交通流分布最终会达到理论分析所给出的某种平衡;在某些路网环境下,不发布诱导信息交通流分布能形成良好的稳定博弈平衡,但在某些路网环境下,路网交通流分布会形成非稳定博弈平衡,不能充分利用整个路网的通行能力,需要采取一定的管理措施。
交通工程;交通流分布;模糊博弈;路径选择;自学习机制
0 引言
驾驶员出行选择行为会对道路交通流的分布产生影响,文献[1-6]研究了无交通诱导或有交通诱导下驾驶员的出行选择对交通流分布的影响。已有的大部分研究假设驾驶员完全理性,这不完全符合现实。此外,在实际交通网络中,交通诱导系统建设需要成本支出,因此有必要分析基于驾驶员有限理性和无诱导信息条件下路网交通流的分布平衡状况,用以确定该路网系统是否有必要建设交通诱导系统,发布诱导信息。
刘建美等[3-5]提出了基于有限理性的博弈出行模型,并重点讨论了最优反应动态学习机制条件下的博弈模型,得出了在无诱导信息条件下有限理性的博弈模型平衡鞍点,但该模型仅考虑了其他驾驶员的决策对自身决策的影响,并没有考虑驾驶员自身的决策影响。然而在实际出行中,对驾驶员路径选择影响最大的是近期经验[7]。笔者在基于行为强化理论的基础上,将驾驶员视为具有有限理性,考虑驾驶员决策的相互影响及自身驾驶经验对路径选择决策的影响,提出有限理性条件下的自学习机制,研究基于有限理性模糊博弈的无诱导信息条件下的车辆路径选择对交通流的分布影响问题。
1 自学习机制
交通出行是一个多人参与的复杂社会活动,出行选择必然受到多方面的影响。首先,虽然驾驶员在出行前追求的是自身利益的最大化,但是其在做出路径选择策略时会受到其他驾驶员决策的影响,即驾驶员之间存在博弈关系[7]。其次,受驾驶员自身的局限性限制(如信息了解不全面、判断不准确等),驾驶员并不是完全理性地做出决策,故应将驾驶员看作是有限理性的决策者。最后,驾驶员每次出行所对应的交通状况不是固定不变的,驾驶员要在多次出行中学习和调整策略,从而达到自己的出行期望,故应将驾驶员的出行过程看作是一个学习过程来讨论。综上所述,驾驶员的出行路径选择过程应作为一个有限理性博弈过程来研究。以往的研究包括最优反应动态模型[6]、复制者动态模型[8]和虚拟行动模型[9]这三大有限理性博弈中经典的学习模型,要求局中人对其他博弈方的决策策略有一定的了解。然而在驾驶员的实际出行选择中,驾驶员很难了解到其他大部分出行者的路径选择策略,故有学者提出驾驶员的策略选择更多地取决于自身的近期经验[7]。
Skinner的操作条件反射理论(也称行为强化理论)认为:人或动物为了达到某种目的,会采取一定的行为作用于环境,当这种行为的后果对他有利时,这种行为就会在以后重复出现;不利时,这种行为就减弱或消失[10]。人们可以用这种正强化或负强化的办法来影响行为的后果,从而修正其行为[11]。
因此,本文以在出行之前驾驶员对行程时间有一个模糊预期为基础,认为博弈的演化过程中局中人是一种自我学习行为,提出了自学习机制:若驾驶员第k次(k为驾驶员车辆路径选择次数)选择的路径行程时间能达到模糊预期,即驾驶员对第k次决策的收益感到满意,则驾驶员第k+1次将会继续选择该路径;若当驾驶员对第k次的路径选择收益的满意度为差时,则其第k+1次将会选择其他路径;当驾驶员对k次的路径选择收益的满意度为一般时,则驾驶员第k+1次将会以一定概率选择其他路径。
2 模型建立
2.1模型基本假设
出行时间的长短是影响路径选择最重要的标准[12],美国联邦总局(BPR)提出路段行程时间函数[13]:
(1)
式中,T为自由行驶时(交通量为零)的路段行程时间;c为路段通行能力;q为路段实际交通量;δ和γ为参数,一般取δ=0.15,γ=4。
本文以驾驶员的实际行驶时间作为驾驶员选择某条路径所获得的收益。考虑如图1所示的简单路网,A点到B点有L1,L2两条路径,其路通行能力分别为C1,C2,表示驾驶员第k次通过L1,L2的实际交通量;t1,k,t2,k为驾驶员第k次通过、到达B点的实际通行时间;t0为驾驶员从A点开往B点的期望时间。
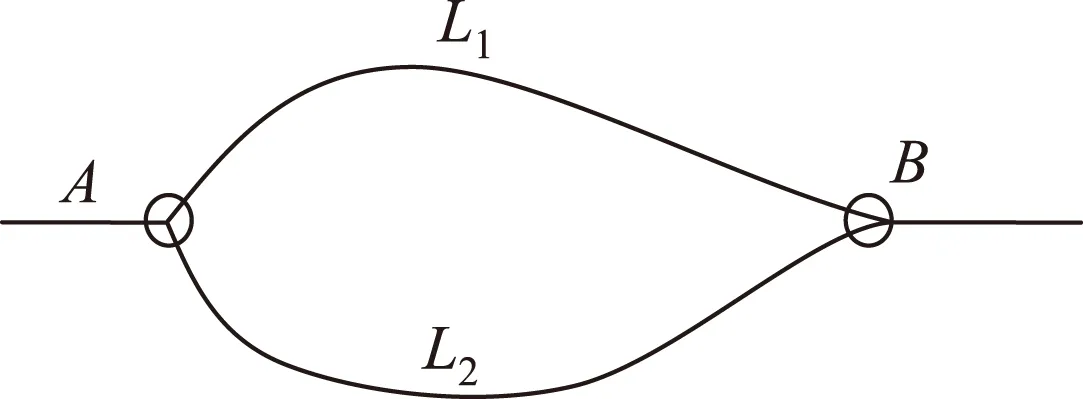
图1 路网示意图Fig.1 Schematic diagram of road network
2.2满意度隶属函数
满意度是指驾驶员对从A点开往B点所花实际时间的满意程度,它是个模糊的概念。隶属函数是模糊数学的一种理论,它的作用是将模糊信息定量化。故用隶属度函数来确定驾驶员满意度,其取值本身也反映了从A点开往B点所花实际时间对驾驶员满意度的隶属程度。取研究范围论域U=(0,+∞), 模糊集A1,A2,A3分别表示“满意”、“一般”、“差”,则它们的隶属函数分别为[14]:
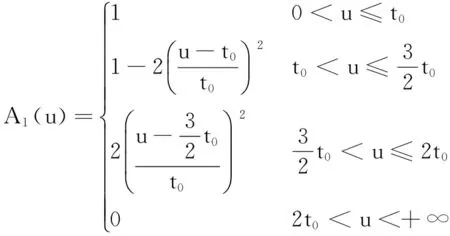
(2)

(3)
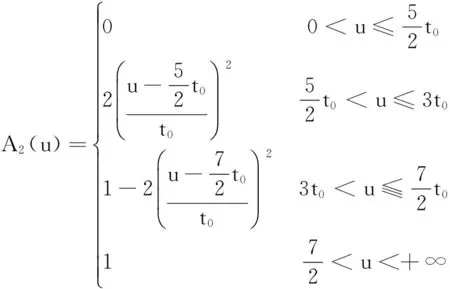
(4)
式中u为论域内任一元素。
若Max{A1(t),A2(t),A3(t)}=A1(t),则t∈A1,驾驶员对实际驾驶时间t的感受为“满意”;若Max{A1(t),A2(t),A3(t)}=A2(t),则t∈A2,驾驶员对实际驾驶时间t的感受为“一般”;若Max{A1(t),A2(t),A3(t)}=A3(t),则t∈A3,驾驶员对实际驾驶时间t感受为“差”。若驾驶员对实际驾驶时间感觉满意,则令其收益为1;若驾驶员对实际驾驶时间感觉一般,则令其收益为0;若驾驶员对实际驾驶时间感觉差,则令其收益为-1。建立路径L1和L2的时间感受收益函数Ei,k(ti,k):
(5)
式中,Ei,k(ti,k)为第k次路径i上的驾驶员的收益;ti,k为第k次路径Li上的车辆实际行驶时间。
2.3博弈模型的建立
当驾驶员的第k次收益为满意时,则其第k+1次选择将与第k次选择保持相同路径;而当驾驶员对第k次路径选择收益的满意度为差时,则其第k+1次将会选择其他路径;当驾驶员对k次路径选择收益的满意度为一般时,则驾驶员将会有β的概率选择其他路径。设每次博弈时参与的车辆总数一定,q1,k和q2,k分别为第k次博弈中路径L1和L2上的车流量,则q1,k+q2,k=Q(Q为参与博弈的车辆总数)。若Gk为局中人集合,Sk为局中人选择策略集合,UGk为局中人选择策略收益集合,此博弈的战略表达式如下:
局中人:Gk∈{q1,k,q2,k},k=1,2,3,…,n;
局中人策略集:Sk∈{L1,L2};
局中人收益函数:UGk∈{E1,k(t1,k),E2,k(t2,k)}。
2.4模型初始状态
设q1,0和q2,0为路径L1和L2上的初始流量,t1,0和t2,0为路径L1和L2上的初始行驶时间,则在自学习机制下,初始状态将出现如下9种情形(为方便行文,若E1,0(t1,0)=1,E2,0(t2,0)=1,则记为(1,1)状态;若E1,0(t1,0)=1,E2,0(t2,0)=0,则记为(1,0)状态),其余状态类推。
情形1:(1,1)状态,则q1,1=q1,0,q2,1=q2,0;
情形2:(1,0)状态,则q1,1=q1,0+βq2,0,q2,1=(1-β)q2,0;
情形3:(1,-1)状态,则q1,1=q1,0+q2,0,q2,1=0;
情形4:(0,1)状态,则q1,1=(1-β)q1,0,q2,1=βq1,0+q2,0;
情形5:(0,0)状态,则q1,1=βq2,0+(1-β)q1,0,q2,1=βq1,0+(1-β)q2,0;
情形6:(0,-1)状态,则q1,1=(1-β)q1,0+q2,0,q2,1=βq1,0;
情形7:(-1,1)状态, 则q1,1=0,q2,1=q1,0+q2,0;
情形8:(-1,0)状态,则q1,1=βq2,0,q2,1=q1,0+(1-β)q2,0;
情形9:(-1,-1)状态,则q1,1=q2,0,q2,1=q1,0。
3 模型分析
由于情形2和4、3和7、6和8类似,所以只需要讨论情形1,2,3,5,6和9这6种情形。
情形1:
t1,1∈A1,t2,1∈A1,则q1,1=q1,0,q2,1=q2,0。
∵q1,1=q1,0,q2,1=q2,0,
∴t1,1=t1,0,t2,1=t2,0,
∴t1,1∈A1,t2,1∈A1,
∴q1,2=q1,1,q2,2=q2,1,
⋮
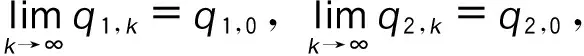
即情形1最终将达到稳定平衡。
同理可证: 情形3和9最终将达到谷峰平衡、交替平衡。
情形2:
t1,0∈A1,t2,0∈A2,则q1,1=q1,0+βq2,0,q2,1=(1-β)q2,0,
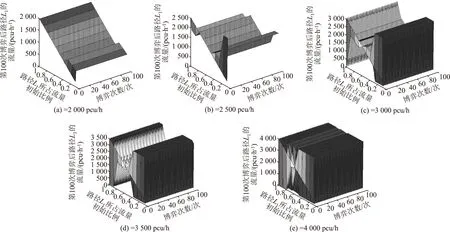
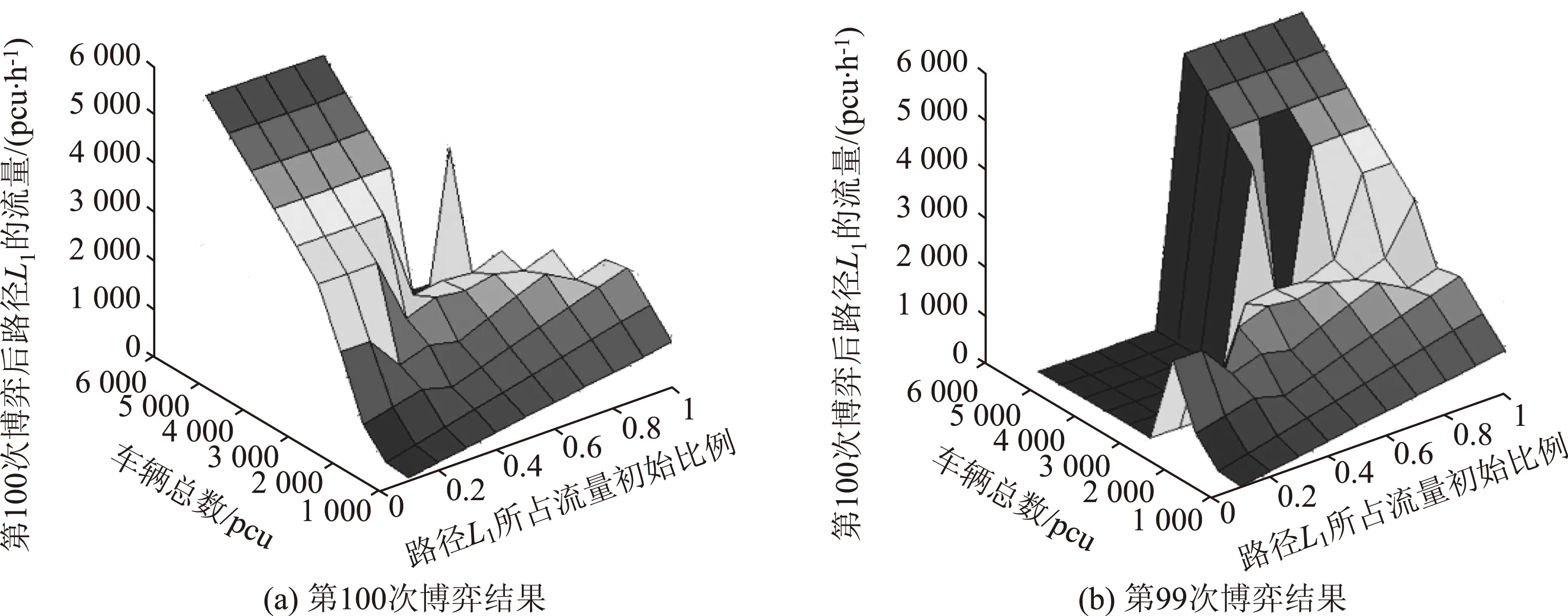
∴q1,1>q1,0,q2,1 ∴t1,1∈A1或A2或A3,t2,1∈A1或A2。 所以,情形2可能会演化为情形1,3,6或依旧为情形2,当其演化为其他情形时,其最终博弈结果将与其他情形相同。因此,在此情形中只考虑其依旧为情形2的情况。为方便起见,后面讨论的情形均只考虑其保持原情形不变的情况(不管情形第几次博弈转换为其他情形,其最终博弈结果将与转换后的情形博弈结果相同,故不予一一讨论)。 考虑其保持情形2不变,则: t1,1∈A2,t2,1∈A1, ∵q1,2=(1-β)q1,1,q2,2=q2,1+βq1,1, ⋮ q1,2k=(1-β)q1,2k-1,q2,2k=q2,2k-1+βq1,2k-1, q1,2k+1=q1,2k+βq2,2k,q2,2k+1=(1-β)q2,2k, ∴q1,2k+1-q1,2k-1=(1-β)2(q1,2k-1-q1,2k-3), ∴q1,2k+1-q1,2k-1与q1,2k-1-q1,2k-3的符号一致, ∴q1,2k+1-q1,2k-1与q1,3-q1,1的符号一致, ∴数列{q1,2k+1}单调。 又 ∵0≤q1,2k+1≤Q, 同理可得: 情形2最终博弈结果为交替平衡。 情形5: t1,0∈A2,t2,0∈A2, 则q1,1=βq2,0+(1-β)q1,0, q2,1=βq1,0+(1-β)q2,0。 I:q2,0>q1,0时, ∵q2,0>q1,0, ∴q1,1=q1,0+β(q2,0-q1,0)>q1,0, ∴q2,1 ∴t2,1 又t1,1∈A2或A3,t2,1∈A1或A2, 因为考虑其保持情形5不变,则: q2,k+1=β+(1-β)q2,k=q2,k+β(Q-2q2,k), q1,k+1=q1,k+β(Q-2q1,k), q2,k+1-q2,k=(q2,k-q2,k-1)(1-2β), 而q2,1-q2,0=β(q1,0-q2,0)>0, ∴q2,k+1-q2,k>0, ∴数列{q2,k}单调递增,又0≤q2,k≤Q, ∴q2,k+1-q2,k与q2,k-1-q2,k-2同号, ∴q2,k+1-q2,k与q2,3-q2,1同号, 而q2,3-q2,1=2β(1-β)(1-2β)(q2,0-q1,0)>0, ∴q2,k+1>q2,k, ∴ 数列{q2,2k+1} 单调递增。 又0≤q2,2k+1≤Q, 因此,情形5最终将达到稳定平衡。 情形6: t1,0∈A2,t2,0∈A3,则q1,1=(1-β)q1,0+q2,0,q2,1=βq1,0。 因为考虑其保持情形6不变,则: q2,1=(1-β)q2,0+q1,1,q1,1=βq2,0, ∴t2,1∈A3,t1,1∈A2, ∴q2,2=βq1,1=β2q2,0, q1,2=Q-β2q2,0, ⋮ ∴∃ξ∈N, 使得:t1,ξ∈A1,t2,ξ∈A3, 即在ξ次博弈后,情形6会演化为情形3。 所以,情形(6)的博弈结果为峰谷平衡。 不同初始状态下的博弈结果如表1所示。 表1 不同初始状态下的博弈结果Tab.1 Game results in different initial states 图2 第k次博弈中路径L1上的流量Fig.2 Traffic volume of path L1 in kth game 图3 不同初始状态下第100和99次的博弈结果Fig.3 Results of 100th and 99th games in different initial states 将操作条件反射理论应用于驾驶员的车辆路径选择行为中,建立了基于行为强化理论的自学习机制。将驾驶员的行程时间感受作为驾驶员的路径选择收益,建立了基于有限理性模糊博弈无诱导信息条件下的车辆路径选择模型。通过理论分析给出了模型博弈结果。数值仿真结果表明:(1)在无诱导信息条件下,路网的交通流分布最终会达到理论分析所给出的某种平衡;(2)在路网交通流总量一定的条件下,初始状态不同,博弈结果的平衡状态可能不同;(3)在某些路网环境下,不发布诱导信息,交通流分布能形成良好的稳定博弈平衡;(4)但在某些路网环境下,路网交通流分布会形成非稳定博弈平衡,不能充分利用整个路网的通行能力,需要采取一定的管理措施。 References: [1]李振龙.诱导条件下驾驶员路径选择行为的演化博弈分析[J].交通运输系统工程与信息,2003,3(2):23-27. LIZhen-long.AStudyofRouteChoiceBehaviorofDriversBasedontheEvolutionaryGameundertheConditionofTrafficFlowGuidance[J].JournalofTransportationSystemsEngineeringandInformationTechnology,2003,3(2):23-27. [2]鲁丛林.诱导条件下的驾驶员反应行为的博弈模型[J].交通运输系统工程与信息,2005,5(1):58-61.LUCong-lin.TheModelsofDriver’sResponseBehaviorwithGameTheoryunderGuideInformation[J].JournalofTransportationSystemsEngineeringandInformationTechnology,2005,5(1):58-61. [3]刘建美,马寿峰.基于有限理性的个体出行路径选择进化博弈分析[J].控制与决策,2009,24(10):1450-1454. LIUJian-mei,MAShou-feng.EvolutionaryGameModeaboutIndividualTravelRouteChoiceBasedonBoundedRationality[J].ControlandDecision, 2009,24(10):1450-1454. [4]LIUJM,MASF,HUANGCC,etal.ADimension-reducedMethodofSensitivityAnalysisforStochasticUserEquilibriumAssignmentModel[J].AppliedMathematicalModelling,2010,34(2):325-333. [5]LIUJM,MASF.AlgorithmsofGameModelsonIndividualTravelBehavior[C]//The8thInternationalIEEEConferenceofChineseLogisticsandTransProfessionals.Chengdu:IEEE,2008: 3060-3066. [6]刘建美,马寿峰,马帅奇.多种博弈个体出行模型的比较与分析[J].统计与决策,2014(2):52-54. LIUJian-mei,MAShou-feng,MAShuai-qi.ComparisonandAnalysisofaVarietyofIndividualTravelModelGames[J].StatisticsandDecision,2014(2):52-54.[7]YANGH,KITAMURAR,JOVANISPP,etal.ExplorationofRouteChoiceBehaviorwithAdvancedTravelInformationUsingNeuralNetworkConcepts[J].Transportation,1993,20(2):199-223. [8]谢识予.经济博弈论[M]. 2版. 上海:复旦大学出版社,2002. XIEShi-yu.EconomicGameTheory[M]. 2nded.Shanghai:FudanUniversityPress, 2002. [10]王济川,郭丽芳.抑制效益型团队合作中“搭便车”现象研究: 基于演化博弈的复制者动态模型[J].科技管理研究,2013,12(21):191-195. WANGJi-chuan,GUOLi-fang.StudyonInhibitionof“Free-riding”PhenomenoninTeamCooperation-basedonReplicatorDynamicModelofEvolutionaryGameTheory[J].ScienceandTechnologyManagementResearch, 2013,12(21): 191-195. [11]周元峰.基于信息的驾驶员路径选择行为及动态诱导模型研究 [D].北京:北京交通大学,2007. ZHOUYuan-feng.ResearchonDriverRouteChoiceBehaviorBasedonVMSInformationandDynamicGuidanceModel[D].Beijing:BeijingJiaotongUniversity, 2007. [12]OUTRAMVE,THOMPSONE.DriverRouteChoice[C]//ProceedingsofthePTRCSummerAnnualMeeting.Warwick:UniversityofWarwickUK, 1977:35-42. [13]杨佩坤,钱林波.交通分配中路段行程时间函数研究[J].同济大学学报:自然科学版,1994,22(1):41-44. YANGPei-kun,QIANLin-bo.ResearchonLinkTravelTimeFunctionsforTrafficAssignment[J].JournalofTongjiUniversity:NaturalScienceEdition,1994,22(1):41-44. [14]杨纶标,高英仪,凌卫新.模糊数学原理及应用[M].广州:华南理工大学出版社,2011. YANGLun-biao,GAOYing-yi,LINGWei-xin.FuzzyMathematicalTheoryandApplication[M].Guangzhou:SouthChinaUniversityofTechnologyPress,2011. Influence of Route Choice Behavior on Traffic Distribution PENG Yong1, LI Bang-lan1, ZHOU Dai-ping2 (1. School of Traffic & Transportation, Chongqing Jiaotong University, Chongqing 400074, China;2. Shenzhen New Land Tool Co., Ltd., Shenzhen Guangdong 518000, China) Under the condition of no guidance information, drivers often choose travel route depend on recent experience. Based on the theory of behavior reinforcement, we established the vehicle routing model without guidance information based on finite rational fuzzy game, and the game equilibrium results under different initial conditions are obtained. The numerical simulation result shows that (1) under the condition of no guidance information, the traffic flow distribution of road network will eventually reach a balance which is given by theoretical analysis; (2) in some road network environments, the traffic flow distribution can form a good stable equilibrium game without release the induction information, however, in some other network environments, the traffic flow distribution will form a non-stable equilibrium game, the traffic capacity of the entire network is inadequate utilized, and certain management measures should be taken. traffic engineering; traffic flow distribution; fuzzy game; path selection; self learning mechanism 2015-05-19 国家山区公路工程技术研究中心开放基金项目(gsgzj-2012-12) 彭勇(1973-),男,重庆人,博士,教授.(pengyong@cquc.edu.cn) U491.1 A 1002-0268(2016)08-0140-06 doi:10.3969/j.issn.1002-0268.2016.08.021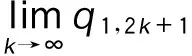
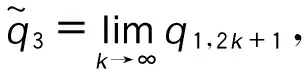
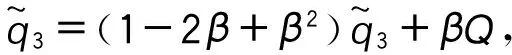

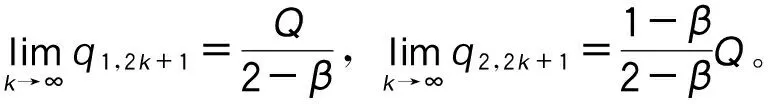
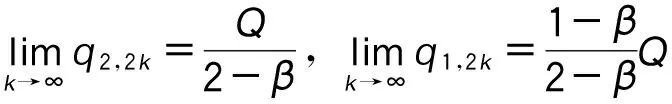
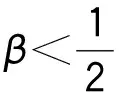
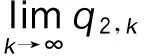
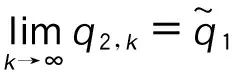
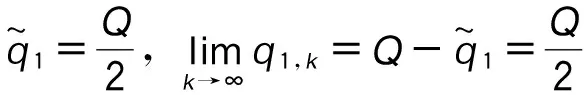
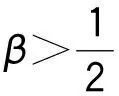
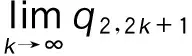
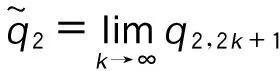
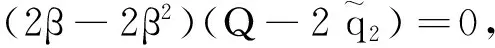
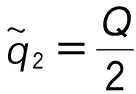
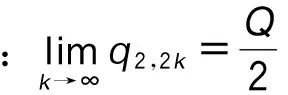
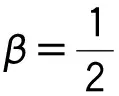
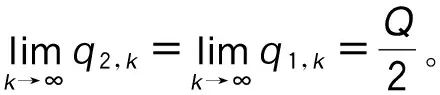
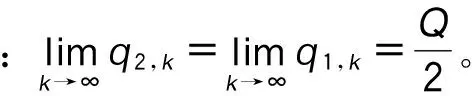
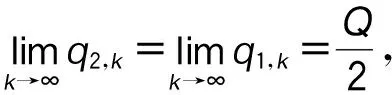
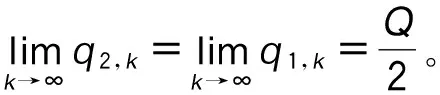
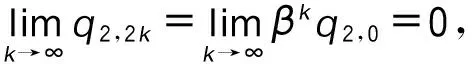
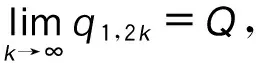
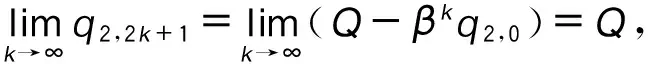

4 结论
