增大截面加固受弯构件的斜截面抗剪承载力计算方法

杨　斌，陈世宏

(广州市市政集团有限公司，广东　广州　510060)



增大截面加固受弯构件的斜截面抗剪承载力计算方法

杨斌，陈世宏

(广州市市政集团有限公司，广东广州510060)

为了使增大截面加固受弯构件的斜截面抗剪承载力的计算更准确和安全，通过对比分析有关设计规范和工程计算实例，认为《公路桥梁加固设计规范》(JTG/TJ22—2008)对增大截面加固构件的斜截面承载力计算公式存在较多错漏，特别是对新增箍筋按所有腹筋截面积分担二期增加的剪力的计算方法提出异议。提出了两种建议计算方法，这两种计算方法均可适用于构件截面单侧增厚和三面围套加固的通用情况，并以工程实例进行验证对比。合并考虑混凝土和箍筋的综合抗剪承载力的第二种建议计算方法简便并相对安全，与普通桥梁构件的设计规范相统一，已被即将颁布的《城市桥梁结构加固技术规程》采用。

桥梁工程；桥梁加固；计算方法；受弯构件；斜截面承载力；增大截面

0　引言

对于增大截面法加固钢筋混凝土受弯构件的斜截面抗剪承载力计算方法，按目前的设计规范，建筑工程采用《混凝土结构加固设计规范》(GB50367—2013)，以下简称《GB加固规范》；桥梁工程采用《公路桥梁加固设计规范》(JTG/TJ22—2008，以下简称《JTG加固规范》。，这两本规范的设计计算方法不同，并且计算结果差别较大。作者在起草行业标准《城市桥梁结构加固技术规程》(以下简称《CJJ加固规程》)的过程中，对比分析这些计算方法的异同，讨论了其中存在的问题，提出了两种建议计算方法，并通过工程实例进行对比计算验证。即将颁布的《CJJ加固规程》最终采用了合并考虑混凝土和箍筋的综合抗剪承载力的第2种建议计算方法，该计算方法简便，相对安全，并与普通桥梁构件的设计规范相统一。

1　现行相关规范的规定

1.1《JTG加固规范》[1]

在《JTG加固规范》中，钢筋混凝土受弯构件在截面受拉区采取单侧增大截面加固后，斜截面抗剪承载力的计算公式如下：

(1)

式中，Vd为加固后构件验算截面处的剪力组合设计值，Vd=Vd1+Vd2，Vd1为新旧材料有效结合前，原构件验算截面处由荷载产生的剪力组合设计值；Vd2为加固后由后期恒载、车辆荷载及其他可变荷载作用的剪力组合设计值。α1为异号弯矩影响系数。α3为受压翼缘的影响系数。ψcs为与原构件斜裂缝有关的修正系数，加固前未出现斜裂缝时，取ψcs=1.0；斜裂缝宽度小于0.2mm时，取ψcs=0.835；斜裂缝宽度大于0.2mm时，取ψcs=0.78。P2为加固后截面纵向钢筋的配筋百分率，P2=100ρ2，ρ2=(As1+As2)/(b2h0)，当P2>2.5时，取P2=2.5。fcu,k为原构件混凝土强度等级。ρsv1为原构件截面内箍筋配筋率，ρsv1=Asv1/(sv1b2)。fsv1为原构件箍筋抗拉强度设计值。ψvb为修正系数，计算公式为：

(2)

1.2《GB加固规范》[2]

在《GB加固规范》中，采用单侧或三面围套增大截面法加固受弯构件时，其斜截面受剪承载力的计算公式如下：

(1)仅在受拉区增设配筋混凝土层，并采用U形箍与旧箍筋逐个焊接时，见图1(a)：

(3)

(2)当增设钢筋混凝土三面围套，并采用加锚式或胶锚式箍筋时，见图1(b)：

(4)

上述式中，αcv为斜截面混凝土受剪承载力系数，对于一般受弯构件取0.7；对于集中荷载作用下的独立梁，取αcv=1.75/(λ+1)，λ为计算截面的剪跨比，可取λ=a/h0，当λ小于1.5时取1.5，当λ大于3时取3，a为集中荷载作用点至支座截面或节点边缘的距离；ftd1，ftd2为新、旧混凝土混凝土轴心抗拉强度设计值；αc为新增混凝土强度利用系数，取αc=0.7；αs为新增箍筋强度利用系数，取αs=0.9；Ac2为三面围套新增混凝土截面面积。

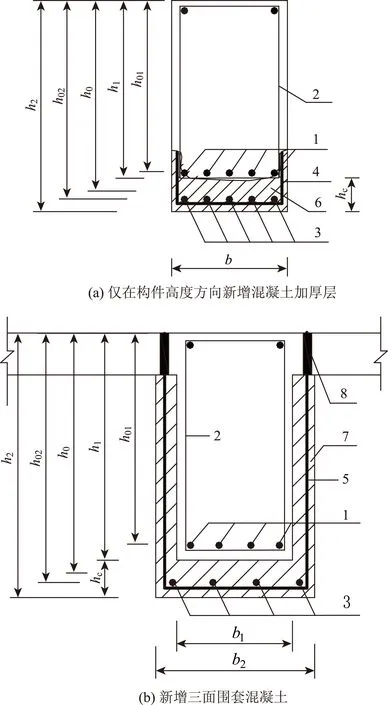
图1　增大截面加固受弯构件的斜截面抗剪承载力计算Fig.1　Calculation of shear capacity of diagonal section of bending member strengthened with enlarged section注：1—原主筋；2—旧箍筋；3—新增主筋；4—新增短U形筋(与旧箍筋对应焊接);5—新增箍筋(与旧混凝土可靠连接)；6—新增受拉区混凝土；7—新增三面围套混凝土；8—孔中用结构胶锚固。

1.3两个规范中计算公式的比较

《JTG加固规范》式(1)是由3部分组成，第1项为构件混凝土与旧箍筋综合抗剪承载力，构件截面积b2h0按加固后截面计算，同时采用了与原构件斜裂缝有关的修正系数ψcs；第2项为原构件的弯起钢筋抗剪承载力；第3项为新增箍筋的抗剪承载力。其中系数ψvb是基于剪力Vd2由原梁箍筋、弯起钢筋和新增箍筋共同承担，按截面分配到新增箍筋的数额系数。

《GB加固规范》分成两种情况考虑(单侧增厚及三面围套)，混凝土提供的抗剪承载力与箍筋提供的抗剪承载力分别计算；新、旧混凝土的抗剪承载力分开计算；新增箍筋提供的抗剪承载力另行计算(三面围套)。

通过对比两个规范的计算公式，有以下不同之处：

(1)适用范围不同。《JTG加固规范》式(1)仅适用于截面受拉区单侧增厚混凝土的加固梁；《GB加固规范》适用范围较大，可适用于单侧增厚和三面围套加固梁。另外，在《GB加固规范》中，没有考虑原梁中设置弯起钢筋的情况。

(2)旧混凝土和旧箍筋提供的抗剪承载力计算方法不同。《JTG加固规范》是参照《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTGD62—2004)的做法，采用半经验半理论的公式来计算新旧混凝土和旧箍筋的综合抗剪承载力Vcs[3]；《GB加固规范》是参照《混凝土结构设计规范》(GB50010—2010)的做法，分别计算旧混凝土的抗剪承载力Vc和旧箍筋的抗剪承载力Vsv[4]。

(3)新增混凝土的抗剪承载力计算方法不同。《JTG加固规范》没有单独列出新增混凝土的抗剪承载力，而是在新旧混凝土和旧箍筋的综合抗剪承载力Vcs计算中，截面有效高度采用受拉区增厚加固后的有效高度h0，间接考虑到了新增混凝土的抗剪承载力，但忽略了新增混凝土与旧混凝土强度等级的差别；《GB加固规范》的加固后抗剪承载力计算中，是在旧混凝土及旧箍筋抗剪承载力的基础上，直接加上新增混凝土的抗剪承载力，考虑了新增混凝土强度利用系数αc=0.7。

(4)新增箍筋的抗剪承载力的计算方法差别甚大。《JTG加固规范》是根据张树仁著《桥梁病害诊断与改造加固设计》中基于试验研究结果的经验计算公式[5]，按新增箍筋在所有腹筋截面积比例来分担二期增加的剪力设计值，这种方法的适用性在下面将进一步讨论；《GB加固规范》的新增箍筋的抗剪承载力计算相对较为直接和简单，和旧箍筋的抗剪承载力计算公式一致，只是引进了新增箍筋强度利用系数αs=0.9。

2　现行规范计算方法存在问题的讨论

2.1《JTG加固规范》计算方法讨论

在《JTG加固规范》的抗剪承载力计算中，存在以下问题值得研讨：

(1)新增箍筋的抗剪承载力计算缺乏试验依据和理论依据

式(1)中第3项(即新增箍筋的抗剪承载力ψvbVd2)的来源是张树仁等著的文献[5-6]，而这些文献针对的加固种类与《JTG加固规范》有区别。文献[5-6]针对的是梁侧边新增粘贴钢板的增大截面加固，《JTG加固规范》是截面单侧增厚混凝土加固，这两种情况相差较大。张树仁教授进行的是9件40cm×18cm矩形梁侧边新粘贴4块t=2～3mm钢板的抗剪承载力试验，并没有进行单侧增厚或三面围套增大截面加固矩形梁的抗剪承载力试验。文献[5-6]中，经过试验数据统计及理论推导，桥梁加固受弯构件斜截面抗剪承载力计算的表达式为：

(5)

式中，AR为与斜裂缝相交的后加补强斜钢板的截面面积，若后加补强钢板为竖直方向布置，则用ARsin45°代替。ψc为与原构件斜裂缝有关的修正系数，加固前未出现斜裂缝时，取ψcs=0.89；斜裂缝宽度小于0.2mm时，取ψcs=0.835；斜裂缝宽度大于0.2mm时，取ψcs=0.78。θs为普通弯起钢筋的切线与水平线的夹角。

文献[5]是张树仁教授针对梁体粘贴钢板进行抗剪加固的情况，主要采用半理论半试验统计的方法，通过按比例分担的形式来计算新增粘贴钢板的抗剪承载力，在目前缺乏更多试验结果和理论分析的情况下，这种方法和成果是富有创造性和可取的。但张树仁教授推导公式(5)是根据粘贴钢板加固斜截面抗剪加固的试验，并没有进行三面围套增大截面抗剪加固的试验，故《JTG加固规范》将式(5)直接用于增大截面的受弯构件斜截面抗剪加固，将增大截面中新增箍筋近似地当作粘贴钢板，这样得到式(1)，这种做法没有试验结果依据，也没有理论推导依据。

(2)存在多处错漏或与引用原著不符的地方

《JTG加固规范》在引用文献[5]时，存在多处与原著不符的地方，也没有在条文说明中说明其原因，对照式(1)和文献[5]，式(1)存在以下4个问题：

①抗剪承载力表达式的第1项，新旧混凝土与旧箍筋综合抗剪承载力表达式，《JTG加固规范》前面的系数0.43×10-3，而在文献[5]中为0.45×10-3。

②抗剪承载力表达式的第1项，与原构件斜裂缝有关的修正系数ψcs，在《JTG加固规范》的规定是“加固前未出现斜裂缝时，取ψcs=1.0”，应该是有误；文献[5]对ψcs的规定为：加固前未出现斜裂缝时，取ψcs=0.89。这个0.89的来历在文献[6]中有说明，ψcs=λβc+0.45=0.55×0.8+0.45=0.89。

③抗剪承载力表达式的第2项，原构件的弯起钢筋抗剪承载力在《JTG加固规范》为0.75×10-3fsd1Asb1，漏掉sinθs，按文献[5]及文献[7]，应修正为0.75×10-3fsd1Asb1sinθs，其中θs为普通弯起钢筋的切线与水平线的夹角。

④ 抗剪承载力表达式的第3项，新增箍筋的抗剪承载力ψvbVd2在《JTG加固规范》中，系数ψvb的表达式为式(2)；如果将新增箍筋类比粘贴钢板，按照文献[5]，新增箍筋的抗剪承载力应为:

这样，得到：

(6)

式(6)中m为剪跨比，m=M/(Vh0)。式(6)中的系数ψvb与《JTG加固规范》中的式(2)相差很大。而且正如前面所提到的，《JTG加固规范》将新增箍筋与文献[6]中粘贴钢板提供的抗剪承载力进行类比，这种做法本身就存在问题，故式(2)缺乏充足的试验和理论依据。

(3)对《JTG加固规范》式(1)的简单修正

针对《JTG加固规范》存在的上述4个问题，如果按文献[6]的原著对式(1)进行修改，则可得到式(7)：

(7)

式(7)是对式(1)的简单修正，只解决了前面所讲的公式(1)存在的前3个小问题，而最重要的第4个问题(新增箍筋的抗剪承载力计算)还没有得到解决。

2.2《GB加固规范》计算方法讨论

(1)计算公式理论依据充分、应用简便

《GB加固规范》的计算公式与文献[4,7]的公式基本一致，依据充分，便于理解和应用。《GB加固规范》将增大截面加固梁的斜截面受剪承载力验算分成两种情况考虑，即单侧增厚和三面围套；混凝土与箍筋提供的抗剪承载力分别计算；新、旧混凝土的抗剪承载力分开计算；原有箍筋和新增箍筋的抗剪承载力也是分开计算。目前对钢筋混凝土梁抗剪加固试验研究均是以此作为理论基础[8-10]。

(2)混凝土与箍筋抗剪承载力的分开计算

鉴于我国建筑和桥梁这两类结构的设计体系和习惯不同，对于受弯构件抗剪承载力计算，在建筑领域，按照文献[2，4]的规定，混凝土与箍筋的抗剪承载力是分开计算的；在桥梁领域，按照文献[1，3]的规定，混凝土与箍筋的抗剪承载力是合并计算的，主要是依据试验结果统计分析，并比建筑领域计算出来的抗剪承载力的安全储备稍高。

(3)新增箍筋的抗剪承载力计算与《JTG加固规范》差别很大

《GB加固规范》对新增箍筋的抗剪承载力直接进行计算，理论依据更强，方法简单清晰。在单侧增厚加固的情况下，视作没有新增箍筋，不进行计算；在三面围套加固的情况下，新增箍筋提供的抗剪承载力另行计算，参照旧箍筋的计算公式，引入一个新增箍筋强度利用系数αs=0.9。

3　笔者建议的计算方法

鉴于《JTG加固规范》的计算公式(1)存在前面所述的一些问题，特别是新增箍筋的抗剪承载力计算方面缺乏依据，有以下两种途径来解决此问题。

3.1建议方法1：分别计算新增混凝土和新增箍筋的抗剪承载力

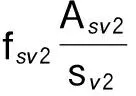
(8)

式中，b1为构件加固前的截面腹板宽度；h01为构件加固前的截面有效高度；P1为加固前计算截面纵向钢筋的配筋百分率，P1=100ρ1，ρ1=As1/(b1h01)，当P1>2.5时，取P1=2.5；ρsv1为原构件截面内箍筋配筋率，ρsv1=Asv1/(sv1b2)。

3.2建议方法2：合并考虑新旧混凝土和新旧箍筋的综合抗剪承载力

这种方法是按照桥梁结构计算的习惯，将新增箍筋与原有箍筋、旧混凝土、新增混凝土全部综合在一起考虑增大截面加固后的综合抗剪承载力，也就是说把二次受力的加固构件当成一次成形的构件来计算抗剪承载力，形成式(9)：

(9)

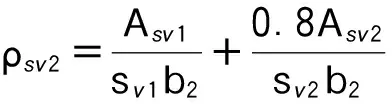
即将颁布的《城市桥梁加固技术规程》采用的第2种方法，即式(9)，该规程是按一次受力构件的计算公式来计算增大截面后的构件混凝土和箍筋的共同抗剪承载力Vcs；构件截面宽度取加固后的构件截面宽度b2。

截面高度取加固后的截面有效高度h0，h0=h2-as，as为加固后构件受拉区纵向普通钢筋As1和As2的合力点至截面受拉区边缘的距离，as按式(10)计算:

(10)

式中hc为构件在受拉区的新增混凝土加厚层厚度。

4　计算实例

某等高度矩形截面简支梁(见图2)，I类环境条件，安全等级为二级。截面尺寸b1×h1=300mm×400mm。采用C30混凝土，HRB335级钢筋。剪力验算截面配置纵向受拉钢筋为4φ22(As1=1 520mm2)，as1=45mm；箍筋为双肢φ8@150mm；配有弯起钢筋2φ22(Asb=760mm2，弯起钢筋切线与水平线的夹角θs=45°)，加固前原构件斜裂缝宽度小于0.2mm。由于荷载等级提高，剪力设计值提高。采用增大截面法加固，矩形梁底部加厚层厚度为100mm，新增钢筋采用HRB400钢筋5φ22(As2=1 900mm2)，as2=45mm；矩形梁两侧各加厚75mm，新增双肢φ10箍筋(HPB300)@150mm，新增箍筋植入原结构中12～15d。新增混凝土为C35。已知第一阶段原构件验算截面的剪力组合设计值为Vd1=100kN，加固后构件验算截面由第二阶段后加荷载引起的新增剪力组合设计值为Vd2=180kN，试验算加固后梁控制截面的斜截面抗剪承载能力[11]。

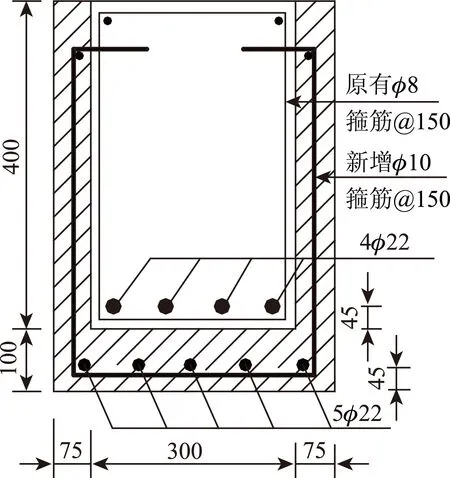
图2计算实例(单位：mm)Fig.2　Calculation example (unit:mm)

分别采用不同规范、规程中的计算方法，得出的计算结果见表1。

从本计算实例的结果可看出，不同的计算方法得到不同的计算结果，其中按照《GB加固规范》计算出来的加固后斜截面抗剪承载力最大(V=438.1kN)，即安全储备相对较小；按照修正后的《JTG加固规范》计算出的加固后斜截面抗剪承载力最小(V=316.1kN)，即安全储备相对较大；而按照《CJJ加固规程》，加固后抗剪承载力V=345.1kN，比修正后的《JTG加固规范》计算结果大9.2%。这样看起来采用“修正的《JTG加固规范》”计算方法更安全，应该推荐使用。但实际上，如前所述，该方法同样也与《JTG加固规范》一样，对新增箍筋的抗剪承载力按照所有腹筋截面积分担二期增加的剪力，这种计算方法缺乏足够的理论和试验依据，并通过其他工程实例试算，不同计算参数的计算结果离散性偏差较大[12]。综上所述，《CJJ加固规程》最终采用本文的建议方法2。

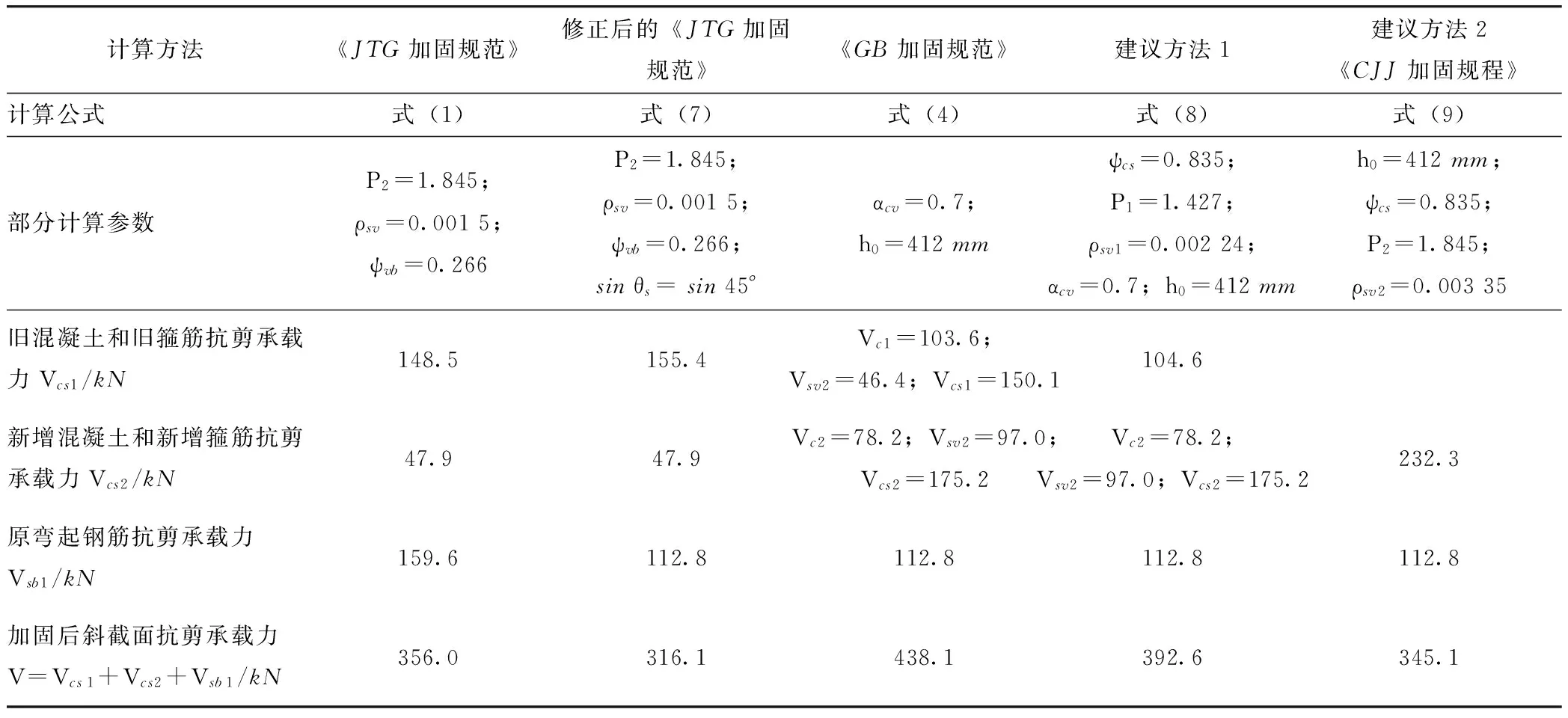
表1　不同计算方法的计算结果对比表Tab.1　Comparison of calculation results of different calculation methods

注：《GB加固规范》Vcs1=Vc1+Vsv1,Vcs2=Vc2+Vsv2。

5　结论

(1)《JTG加固规范》对斜截面加固的计算公式(1)，存在几个明显的错漏或与原著不符的问题，需进行修改，建议规范编制单位在版本更新时进行修改。

(2)《GB加固规范》计算公式理论依据充分，应用简便，但安全储备比《JTG加固规范》小，故《GB加固规范》只适用于房屋建筑类的结构(主要承受静力荷载的结构)。而对于主要承受动力荷载的桥梁构件，应采用《JTG加固规范》或《CJJ加固规程》的计算方法。

(3)《JTG加固规范》对于新增箍筋的抗剪承载力，是按照新增箍筋在所有腹筋截面积比例来分担二期增加的剪力，这种计算方法没有充分的试验数据和理论依据，经过试算，其结果与是否设弯起钢筋、二期新增剪力值等因素密切相关，即使是配置相同的新增箍筋Asv2/sv2，其新增抗剪承载力或大或小，偏差较大。建议对新增箍筋的承载力再进行充分的理论分析和试验研究。

(4)《CJJ加固规程》的计算方法(即本文的建议方法二)虽然没有考虑二次受力构件的影响，但其计算原理易于理解，计算公式简便易用，计算结果有一定的安全储备，可以较好地适用于桥梁构件的计算。

References:

[1]JTG/TJ22—2008，公路桥梁加固设计规范 [S].

JTG/TJ22—2008,SpecificationsforStrengtheningDesignofHighwayBridges[S].

[2]GB50367—2013， 混凝土结构加固设计规范 [S].

GB50367—2013,CodeforDesignofStrengtheningConcreteStructure[S].

[3]JTGD62—2004，公路钢筋混凝土及预应力混凝土桥涵设计规范 [S].

JTGD62—2004,CodeforDesignofHighwayReinforcedConcreteandPrestressedConcreteBridgesandCulverts[S].

[4]GB50010—2010，混凝土结构设计规范 [S].

GB50010—2010,CodeforDesignofConcreteStructures[S].

[5]张树仁，王宗林. 桥梁病害诊断与改造加固设计 [M]. 北京：人民交通出版社，2006.

ZHANGShu-ren,WANGZong-lin.BridgeDiseaseDiagnosisandReinforcementDesign[M].Beijing:ChinaCommunicationsPress, 2006.

[6]张树仁,宋建永,张颂娟. 桥梁加固钢筋混凝土受弯构件斜截面承载力计算方法及试验研究 [J]. 中国公路学报，2003，16(3)：64-68.

ZHANGShu-ren,SONGJian-yong,ZHANGSong-juan.CalculationMethodandTestInvestigationofObliqueSectionConsolidationofReinforcedConcreteBridge[J].ChinaJournalofHighwayandTransport, 2003,16(3):64-68.

[7]叶见曙. 结构设计原理 [M]. 北京：人民交通出版社，2007.

YEJian-shu.StructureDesignPrinciple[M].Beijing:ChinaCommunicationsPress, 2007.

[8]王元栋. 受损钢筋混凝土梁增大截面法抗剪加固研究 [D]. 北京：北京建筑大学，2013.

WANGYuan-dong.ShearStrengtheningofDamagedRCBeamswithMethodofSectionEnlargement[D].Beijing:BeijingUniversityofCivilEngineeringandArchitecturePress, 2013.

[9]张志. 配斜筋锈蚀RC梁的抗剪承载力研究 [D]. 长沙：长沙理工大学，2012.

ZHANGZhi.StudyofShearCapacityofCorrodedRCBeamswithDiagonalReinforcements[D].Changsha:ChangshaUniversityofScience&Technology, 2012.

[10]左印波. 具有斜裂缝钢筋混凝土梁抗剪承载力的试验研究以及数值分析 [D]. 沈阳：东北大学，2011.

ZUOYin-bo.ExperimentalStudyandNumericalAnalysisonShearCapacityofRCBeamswithDiagonalCracks[D].Shenyang:NortheasternUniversity, 2011.

[11]安关峰. 城市桥梁结构加固技术指南[M].北京：中国建筑工业出版社，2015.

ANGuan-feng.TechnicalGuideforStructuralStrengtheningofUrbanBridges[M].Beijing:ChinaBuildingIndustryPress,2015.

[12]邬晓光，白青侠，雷自学. 公路桥梁加固设计规范应用计算示例[M]. 北京：人民交通出版社，2011.

WUXiao-guang,BAIQing-xia,LEIZi-xue.ApplicativeCalculationExampleforSpecificationsofStrengtheningDesignofHighwayBridges[M].Beijing:ChinaCommunicationsPress, 2011.

Methods for Calculating Shear Capacity of Oblique Section of Bending Members Strengthened with Enlarged Section

YANG Bin, CHEN Shi-hong

(GuangzhouMunicipalEngineeringGroupCo.,Ltd.,GuangzhouGuangdong510060，China)

Inordertocalculatetheshearcapacityonobliquesectionofbendingmembersstrengthenedwithenlargedsectionmoreaccuratelyandsafely，throughcontrastiveanalysisofrelevantdesignspecificationsandengineeringcalculationexamples,wethinkthatsomecalculatingformulasforthebearingcapacityonobliquesectionofthemembersstrengthenedwithenlargedsectionhaveseveralmistakesinSpecifications for Strengthening Design of Highway Bridges (JTG/TJ22—2008),particularlywechallengedthecalculationmethodthatthenewstirrupssharethesecondphaseincreasedshearforcebasedontheproportionofallwebreinforcement’ssectionarea.Weproposed2calculationmethodswhichcanbeappliedtothegeneralsituationofunilateralthickeningofthemembersectionandreinforcementof3sidesofthemember,andtestedwiththeengineeringexample.Thesecondproposedmethod,whichconsideredthecomprehensiveshearcapacityofbothconcreteandstirrups,issimpleandrelativelysafe,itisunifiedwiththedesignspecificationofordinarybridgecomponent,anditisadoptedinTechnical Specifications for Strengthening of Urban Bridgesthatwillbeenactedsoon.

bridgeengineering；bridgestrengthening；calculationmethod；bendingmember；bearingcapacityonobliquesection；enlargedsection

2015-06-29

杨斌(1973-)，男，江西丰城人，硕士，高级工程师.(yangbin2345@126.com)

U445.7

A

1002-0268(2016)08-0099-07

doi:10.3969/j.issn.1002-0268.2016.08.015