基于点源透过率测试系统的杂散光标定

徐　亮，高立民，赵建科，刘　峰，周　艳，李朝辉，2，杨　菲，赵　青，2

(1.中国科学院 西安光学精密机械研究所，陕西 西安 710119；2.中国科学院大学，北京100049；3.中国一航西安飞机工业(集团)有限责任公司，陕西 西安 710089)



基于点源透过率测试系统的杂散光标定

徐亮1，2*，高立民1，赵建科1，刘峰1，周艳1，李朝辉1，2，杨菲3，赵青1，2

(1.中国科学院 西安光学精密机械研究所，陕西 西安 710119；2.中国科学院大学，北京100049；3.中国一航西安飞机工业(集团)有限责任公司，陕西 西安 710089)

为了提高点源透过率(PST)测试系统的杂散光测试能力及测试精度，提出并设计了一种标准镜头，用于在大离轴角范围内对系统的杂散光测试范围及测试精度进行标定。利用简单的物理模型设计了一种在实验室内对点源透过率测试系统杂散光测试精度定标的标准镜头；测量了标准镜头的表面物理参数，并将其带入TracePro软件计算出了不同离轴角对应的PST。对设计分析的PST值与实测的PST值进行比较，从而计算得到了该测试系统的测量精度。验证实验表明，该标准镜头的PST分析值与实测值之差优于lg/0.5，满足实验室内对点源透过率测试系统杂散光测量精度进行标定的要求，是PST绝对测量的可靠方法。该项技术为国内PST测试系统的精度校准问题提供了技术保障。

点源透过率测量；杂散光测量；标准镜头；标定；双向反射分布函数

1　引　言

随着我国航天事业的发展，深空探测、火星计划、探月工程等重点工程已迈入一个新的时代，人们对光电设备的杂散光抑制能力也提出了新的要求，视场外杂散光的抑制能力终将成为评价光电设备探测与成像能力的关键指标。航天用光学系统的杂散光主要来源于视场外明亮物体(尤其是太阳) 的强烈辐射，这些辐射经光学系统后发生散射、衍射，并以杂散光形式分布于光学系统的探测器上，从而影响光学系统的探测能力[1]。

针对杂散光的抑制问题，本课题组研制了一种点源透过率(Point Source Transmittance，PST)测试系统。该系统可精确测试光学系统的杂散光抑制能力，并根据实测杂散光对光学系统进行优化设计，通过改进遮光罩来实现消除杂散光的目标。这就要求PST测试系统必须具有高精度，否则不能准确指导光学系统的优化设计[2-3]。PST测试系统的标定是保证测量精度的一个关键技术问题，因此，光学系统PST的测试将转换成系统测量精度的标定。

本文提出了一种基于PST测试系统精确标定的标准镜头。利用该标准镜头的关键表面特性，通过建模分析得出了标准镜头的相对真值PST，并将实测PST与理论PST作比较，以此评价该系统PST的测试精度。

2　点源透过率测试系统介绍

杂散光测量技术在国外已经比较成熟，Utah State University的Space Dynamics Laboratory在20世纪70年代就建立了PST测试装置Black Hole， 其PSRR测试水平可达到10-15。但国内起步较晚。目前，国内关于PST测试技术的研究单位主要有西安光机所、成都光电所、哈工大等。其中，西安光机所研制的点源透过率测试系统可用于测量不同波段、不同视场角下的PST，其原理如图1所示。

图1　点源透过率测试系统原理图

图1中，由光源出射的均匀点源经平行光管耦合扩束后，形成口径为Φ1 m的均匀面光源(用于模拟无穷远处的强光目标源)，穿过黑色双柱罐照亮被测相机光学系统的遮光罩及玻璃表面，形成强杂散光源。在光学系统后焦面放置高灵敏度探测器，用于测量不同离轴角的杂散光光照度。PST定义为光学系统视场外视场角为θ的点源目标的辐射，经光学系统后在像面产生的辐照度Ei(θ，λ) 与其在光学系统入瞳处的辐照度E0(θ，λ)的比值[4]，即：

(1)

从而可推算出被测相机在不同离轴角的PST。然而该系统的测试精度标定问题一直是困惑业界的难题。本文设计了一种标准镜头，放置在测试系统待测光路中，实测其PST值，并将标准镜头的PST理论计算值与其比较来验证系统的测试精度。其精度为：

lg(测量值/理论值)≤0.5.

(2)

(文中简写lg/0.5)

3　点源透过率测试系统标准镜头设计

标准镜头主要应用于点源透过率测试系统的实验室标定，用于验证整个测试系统的测量精度及长期稳定性。因此，标准镜头主要有以下设计要求：第一，光机系统结构简单，对杂散光分析容易，重复性测量精度高；第二，镜头的PST曲线较平缓，便于提高系统的校准精度。

3.1标准镜头的主要技术指标

本文设计的标准镜头的主要性能指标如表1所示。

表1　标准镜头的主要性能指标

3.2标准镜头设计

标准镜头的设计主要分为光学系统设计和遮光罩设计。光学系统设计时除考虑相关光学参数满足任务要求外，光学结构形式要简单，便于杂散光的建模分析。遮光罩的设计采用简单的挡光环模型，对其材料表面涂层的特性进行深入分析，利用不同模型计算其表面双向反射分布函数(Bidirectional Reflectance Distribution Function，BRDF)的散射特性。

3.2.1光学系统设计

标准镜头的光学系统采用简单的三分离式光路结构，如图2所示。由于被校准测试系统采用激光光源，因此标准镜头采用波长为0.65 μm的单色光设计，这种设计也有利于后期标准镜头杂散光的定量建模分析。最终3块玻璃全采用H-Lak3，其设计结果如图3和图4所示，该系统成像质量优良，接近衍射极限，且便于后期的光学装配。

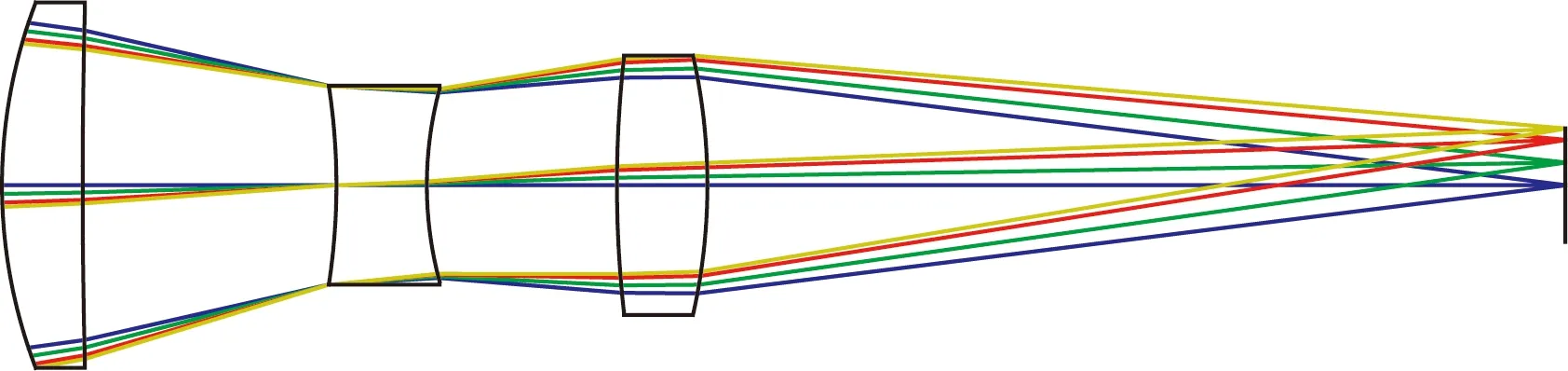
图2　标准镜头的光学系统

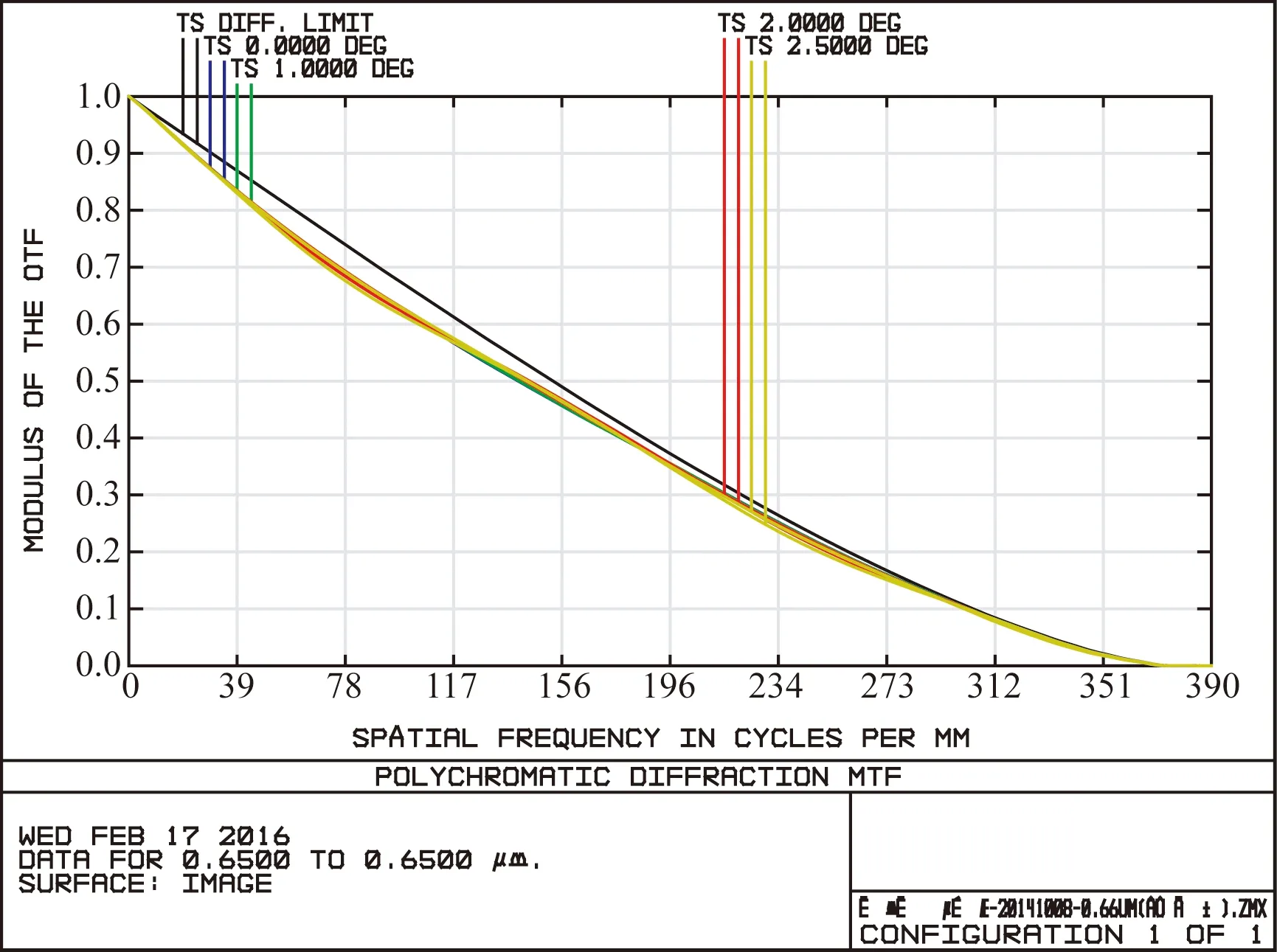
图3　标准镜头传递函数

图4　标准镜头弥散斑

3.2.2遮光罩设计

为了避免背景强辐射源的杂散辐射直接入射到光学系统，本文设置系统遮光罩来阻挡强辐射源的杂散辐射直接通过光学系统入射到探测器焦面，此外到达探测器焦面的强辐射源的杂散辐射能量不能过大，这就要求遮光罩及挡光环表面要尽可能多地吸收杂散辐射。传统的遮光罩不可避免地存在长度过长、重量重、体积大等缺点，更有甚者还会阻挡边缘视场光学的传播。一般来说遮光罩的设计原则如下：

(1)避免非成像光线直接到达像面；

(2)取强杂散辐射源的特定关注入射角度16°为规避角。大于规避角的入射强杂散辐射至少经过两次及以上的散射后才允许进入光学系统，即以光学系统第一表面为二次散射控制面。

(3)边缘视场的正常光线不能被遮光罩遮拦。

首先进行了遮光罩的结构设计。为了简化结构形式，这里采用挡光环梯度布置的遮光罩。挡光环设计最主要的一个原则为：光线从遮光罩外端内壁入射，经过一个挡光环的顶点入射到遮光罩内壁后，由于连接的下一个挡光环的遮拦，使向任意方向散射的光线不能直接到达光学系统的第一表面。

遮光罩对杂散光的抑制主要由内壁表面涂黑漆和自身结构保证，其结构设计原理如图5所示。

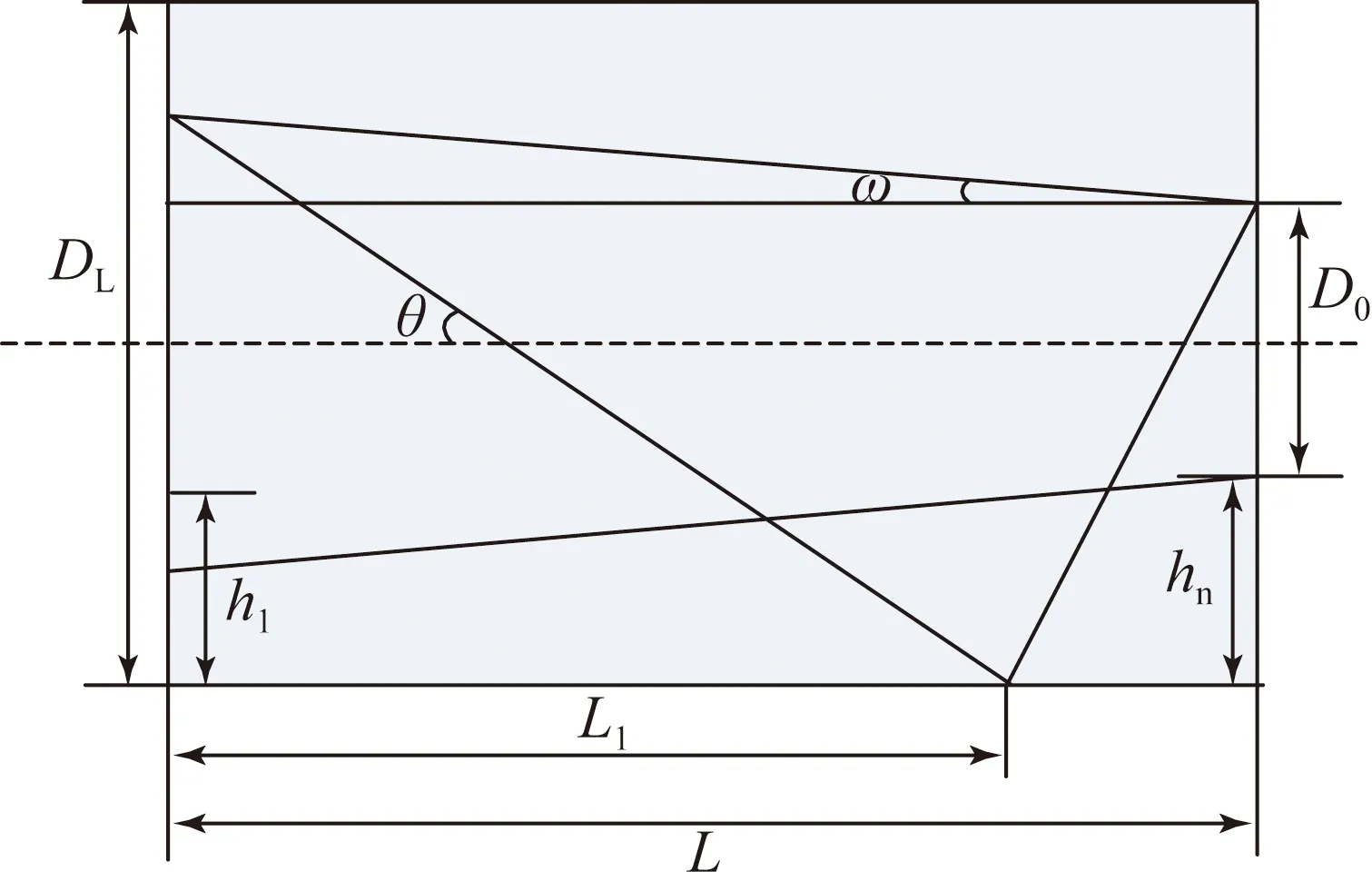
图5　遮光罩设计原理

遮光罩的具体参数计算[5-7]如下：

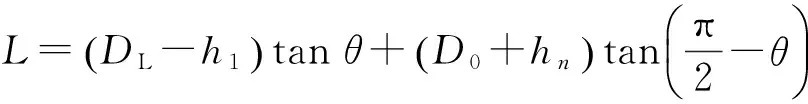
(3)

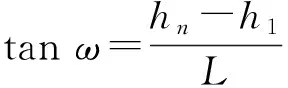
(4)

DL=D0+2hn，

(5)

其中：h1为遮光罩前端设置的挡光环高度；hn为遮光罩同光学系统端的挡光环高度；θ为规避角；D0为光学系统第一片透镜的口径；DL为遮光罩口径；ω为半视场角；L为遮光罩总长。已知：D0=62 mm，ω=2.5°，θ=20°，h1=5 mm，通过计算可得：hn=15.73 mm，DL=93.46 mm，L=245.76 mm。通过在CAD中建模，确定出各级挡光环在外遮光罩上的位置和内径，共需10级挡光环，挡光环厚度均为0.5 mm，如图6所示。

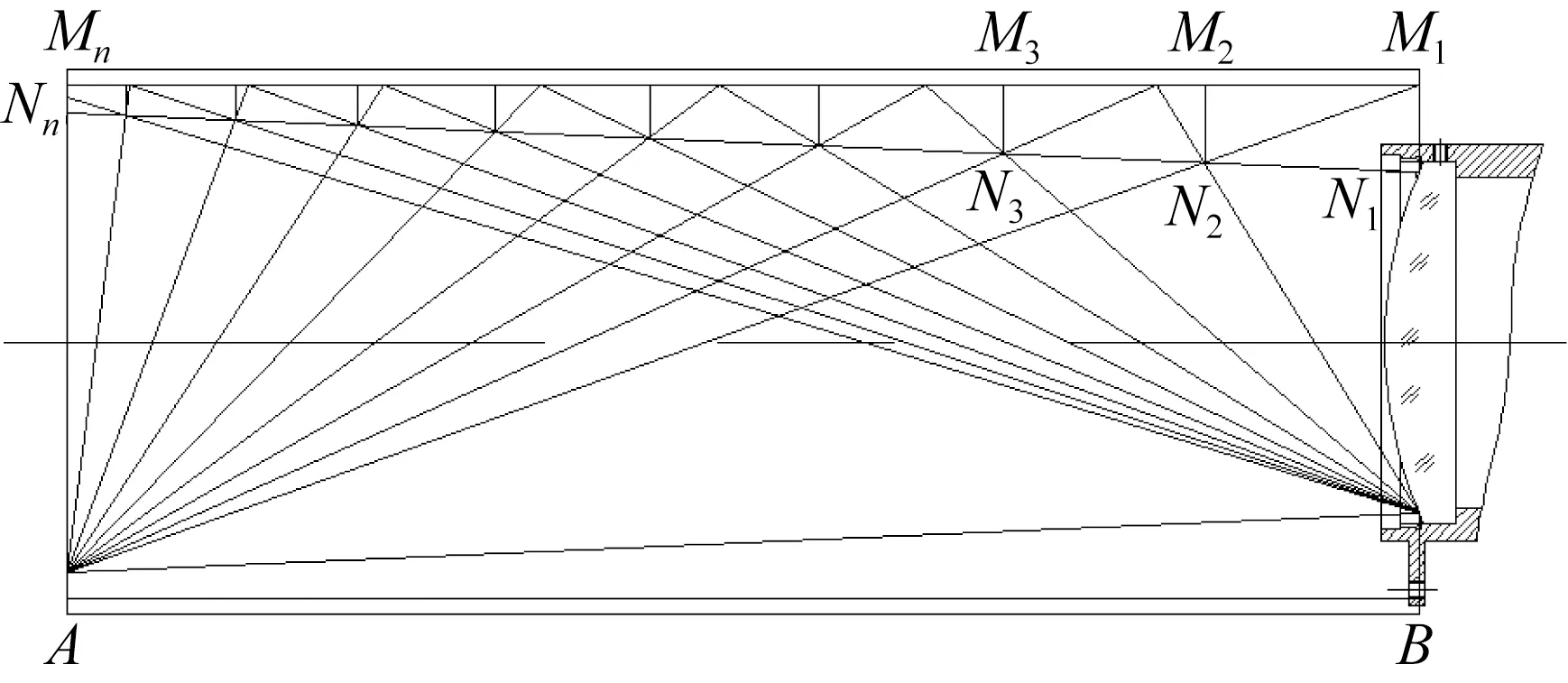
图6　遮光罩设计模型

在标准镜头系统设计完成后，利用Tracepro软件分析其杂散光，并对遮光罩涂层、透镜材料及表面的属性进行设置。遮光罩的表面属性由双向散射分布函数(Bidirectional Scattering Distribution Function，BSDF)来定义，由于透镜元件表面为光滑透明表面，适合使用ABg模型来分析。根据Harvey-Shack模型，当表面粗糙度小于等于波长，即σ≤λ时，材料表面的BSDF为[8-12]：

(6)

(7)

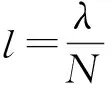
(8)

s=-C.

(9)

其中，ABg模型中的三个参数可以通过Harvey-Shack模型系数进行换算，换算公式如下：

A=b0N，

(10)

B=l-s，

(11)

g=-s.

(12)

则玻璃表面在Tracepro中设置的BRDF参量为A=7.246×10-5，B=0.001，g=2，BTDF参量为A=6.35×10-5，B=0.001，g=2。透镜表面镀增透膜，透射率为0.98，非通光面涂黑，吸收率为0.005。

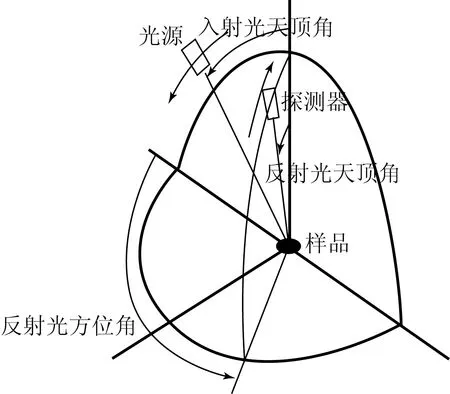
图7　遮光罩涂层样片测试示意图

遮光罩表面涂层是影响其杂散光抑制能力的另外一个重要因素，本文选用AeroglazeZ-306黑漆作为遮光罩涂层。为了将材料的表面特性准确建模，这里利用法国Reflect BRDF测试仪测量此遮光罩样片，测试原理如图7所示，可见光由RGB三色光组成，样品粗糙度满足σ/λ≥1。取光源入射面的方位角为零，探测器对不同方位角(0°到180°每间隔10°扫描一次)，从天顶角为-85° 位置扫描到85°位置(每间隔5°扫描一次)，如图8所示，从而得到整个半球空间的BRDF分布，如图9所示。

(a)样品(正面)(a)Specimen(front)　(b)样品(背面)(b)Specimen(back)

图9　不同入射角度下Z306黑漆测量数据的双对数图

Fig.9Double logarithmic graph of testing data of Z306 under different incident angles

3.2.3标准镜头设计结果仿真分析

由图9可以看出，Z306黑漆散射在小角度近似为朗伯体，随着入射角度的增大，其前向散射特性较为明显。这与以往近似的特征表面后向散射是完全不同的，而ABg模型仅能拟合后向散射特性，故ABg模型不再适用，因此，在Tracepro软件中采用Asymmetric Table模型设置材料属性。用表格积分的形式可准确地评价不同入射角材料表面的散射情况，最终的建模结果如图10所示。

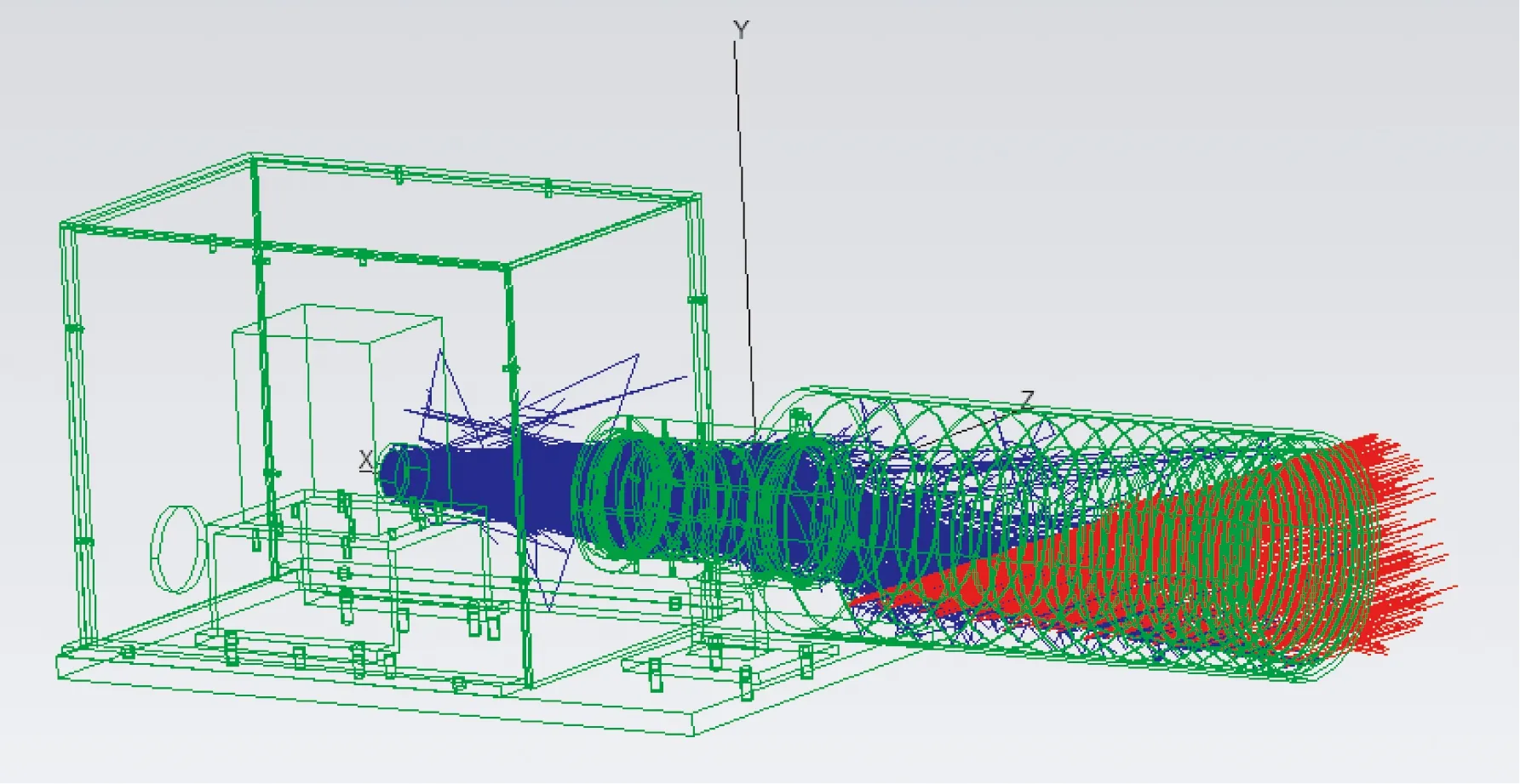
图10　标准镜头PST分析建模图

本文将上述玻璃材料属性及结构表面特性分别建模，带入标准镜头模型中进行分析，最终该标准镜头的PST计算曲线如图11所示。

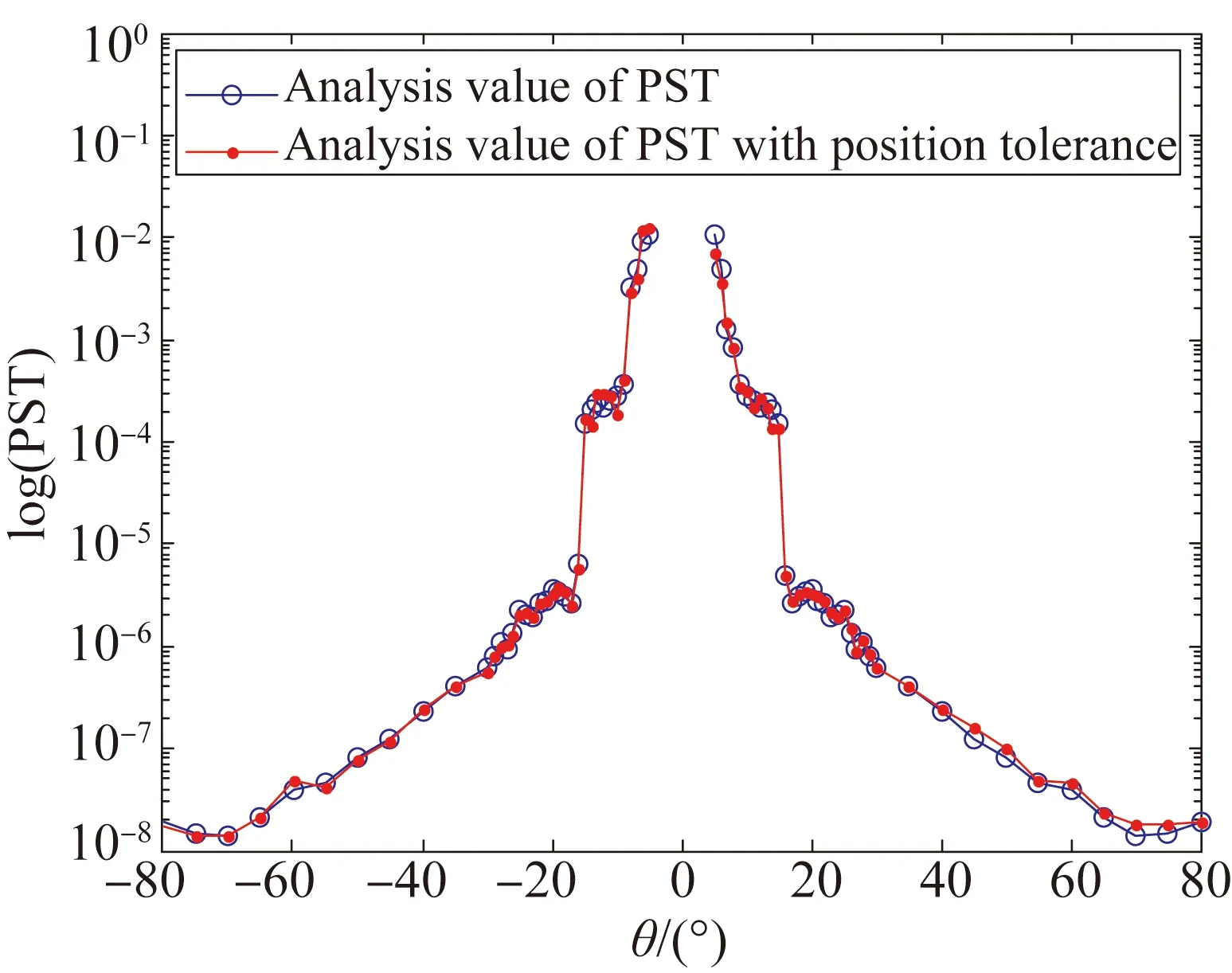
图11校准镜头PST分析值及引入位置公差后PST分析值

Fig.11Analysis values of PST without and with position tolerance for standard lens

由图11可以看出，标准镜头在离轴角为±5°～±80°时PST设计值从10-2降至10-7，完全满足技术指标要求。在规避角为±16°附近，PST迅速下降至10-5，与标准镜头遮光罩消杂散光的设计原则一致，可充分说明该遮光罩设计的有效性。另外，该设计曲线除规避角附近较为陡峭外，其余大角度范围PST曲线均保持平缓，这对于标校整个PST测试系统的测量精度来说是有利的，因为这种设计可大大降低由于光轴对准误差而产生的PST测量误差。

4　标准镜头的杂散光测试与系统校准

作为校准PST测试系统的标准来说，经过准确、详细的理论模型推算，标准镜头的PST设计值可作为理论真值来评价测试系统的准确性及可靠性。这种评价标准也是根据传递函数测试仪的标准镜头评价原则来定义的，即采用标准镜头的理论设计结果作为理论真值，通过多台设备比对的方式来验证标准镜头的准确性。目前，本文的杂散光标准镜头在国内属于第一套，且由于可测试用的PST设备不多，经调研只有西安光机所和上海技物所有两套高精度PST测试系统，最终采用这两套系统进行比对测试。

标准镜头的杂散光设计精度是由光机系统的模型精度及表面属性精度来决定的。其中光机系统的模型精度可通过严格的工艺手段保证，这里将结构的挡光环位置公差(±0.1 mm)和厚度公差(±0.1 mm)带入模型进行建模分析。经分析这部分对系统杂散光产生的误差主要来源于小角度误差，其杂散光的最大分析误差为35%；而喷漆材料表面属性是通过法国Reflect BRDF测试仪精确测试的，其测试精度为0.001%，换算成积分总散射后的合成误差对系统PST的误差总贡献最大为50%。将上述两个分析误差合成后，设计误差最大不超过61%，作为鉴定测试系统PST测试精度，这个设计分析误差远远优于lg/0.5，因此，可将标准镜头分析结果作为标准来验证系统的测试精度。

因此，可根据上述对标准镜头的设计分析结果来验证PST测试系统的测量精度。具体思路是：将标准镜头安装在PST测试系统转台上，测试离轴角为±5°～±80°的PST，将测试结果与理论计算结果进行比较，利用式(2)可计算出PST测试系统的测量精度，测试现场如图12所示。

图12　标准镜头的现场测试图

图13中给出了标准镜头3次测量的PST曲线。从测试结果来看，其不同角度对应的最大PST测量误差为8%，完全满足PST测试系统稳定性的校准要求。从整个测试曲线结果来看，在离轴角为±5°～±80°时PST测试值从10-2降至10-7，在规避角±16°附近，PST测试值也迅速下降至10-5，与标准镜头设计曲线的趋势一致，完全符合设计要求。且该曲线在左视场小角度PST测试值比右视场小角度PST测试值略大一些，这主要是由于镜头光轴对准误差而产生的测试校准误差，然而此误差远远小于系统的PST校准误差(lg/0.5)，不影响最终的系统校准，这也足以说明遮光罩设计的合理性。

图13　标准镜头PST测试值

5　标准镜头对系统校准结果分析

5.1标准镜头的杂散光测试结果

标准镜头先后在西安光机所和上海技物所的PST设备上进行了比对性测试，测试曲线如图14所示。其中两种设备的测试结果比较接近，最大偏离误差为50%，这里将其平均值作为相对真值与设计值进行比较，可判断该标准镜头设计的合理性。从总体上来看，设计结果与实测结果基本一致，完全满足设计与校准要求。

从比对数据来看，测试值略大于设计值，这主要是由于环境的空气散射产生的杂散光造成本底噪声叠加而产生的测量误差。要降低这种误差，只能将环境空气的洁净度提高至千级。

另外，PST在10-2～10-6时，lg(测量值/理论值)最大值为0.43，完全满足指标要求；PST在10-6～10-7时，测量值稍大于设计值，表明系统在大角度PST测试时，双柱罐内大量的散射、反射杂散光直接进入被测镜头视场，产生光污染造成其测量结果偏大，角度越大这种现象越明显。根据此现象测量了环境的PST，发现环境PST大约为10-8，这足以说明环境保障对整个测试精度的影响。

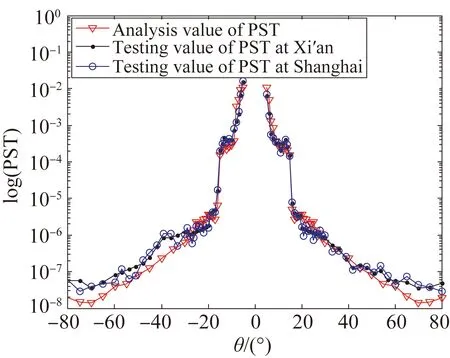
图14　标准镜头PST校准数据比对

与此同时，左右视场在±14°的位置均出现了曲线“回拐”现象，虽然这不影响系统的校准精度，但是这种现象有待于进一步的研究和分析。目前，初步研究认为这种现象有可能由于遮光罩表面材料属性模型分析误差和系统结构加工、装配与理论模型有偏差而产生的，这些对精度的影响及如何控制，将在以后的工作中做深入研究。

5.2系统校准结果分析

标准镜头的研究主要是为了验证PST测试系统的测试精度，并考核该测试系统的稳定性。根据上述测试结果可知，虽然PST在10-2～10-6时，标准镜头的设计值与测试值吻合度较高，可完全应用于系统的校准；但PST在10-6～10-7时，设计值与实测值相差较大，同时全视场范围实测值整体偏大，这些是以后研究的重点，以进一步提高系统的校准精度及校准范围。

根据设计与实测结果可知，该标准镜头的PST校准精度主要受环境光和自体辐射、双柱罐内壁、空气灰尘和定标不确定度等因素的影响，表中百分比是干扰量相对于PST为10-7的比值，具体分析如表2所示。

综上所述，由表2可以看出，在大离轴角测试时，PST测试精度受双柱罐内壁散射、反射的影响较大，如图15所示。在被测镜头转过离轴角30°～80°的过程中，大部分的杂散光将直接进入被测镜头入瞳，产生一次杂散光，这将直接导致PST测量精度降低。若要减小这部分测量误差，应加大双柱罐尺寸，同时降低双柱罐内壁的反射率和散射率。

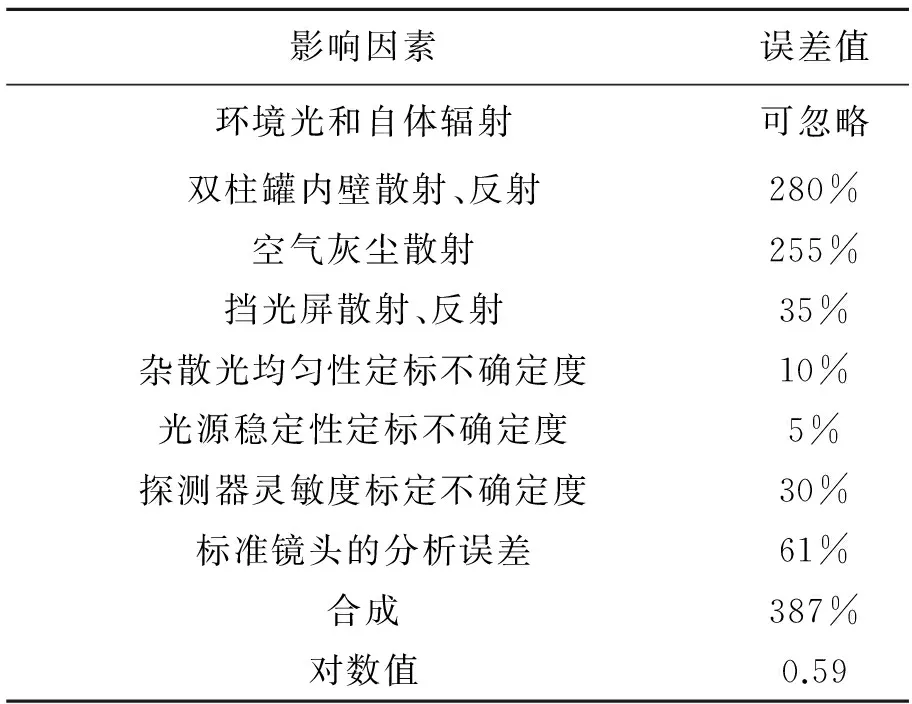
表2　PST测试精度分析表

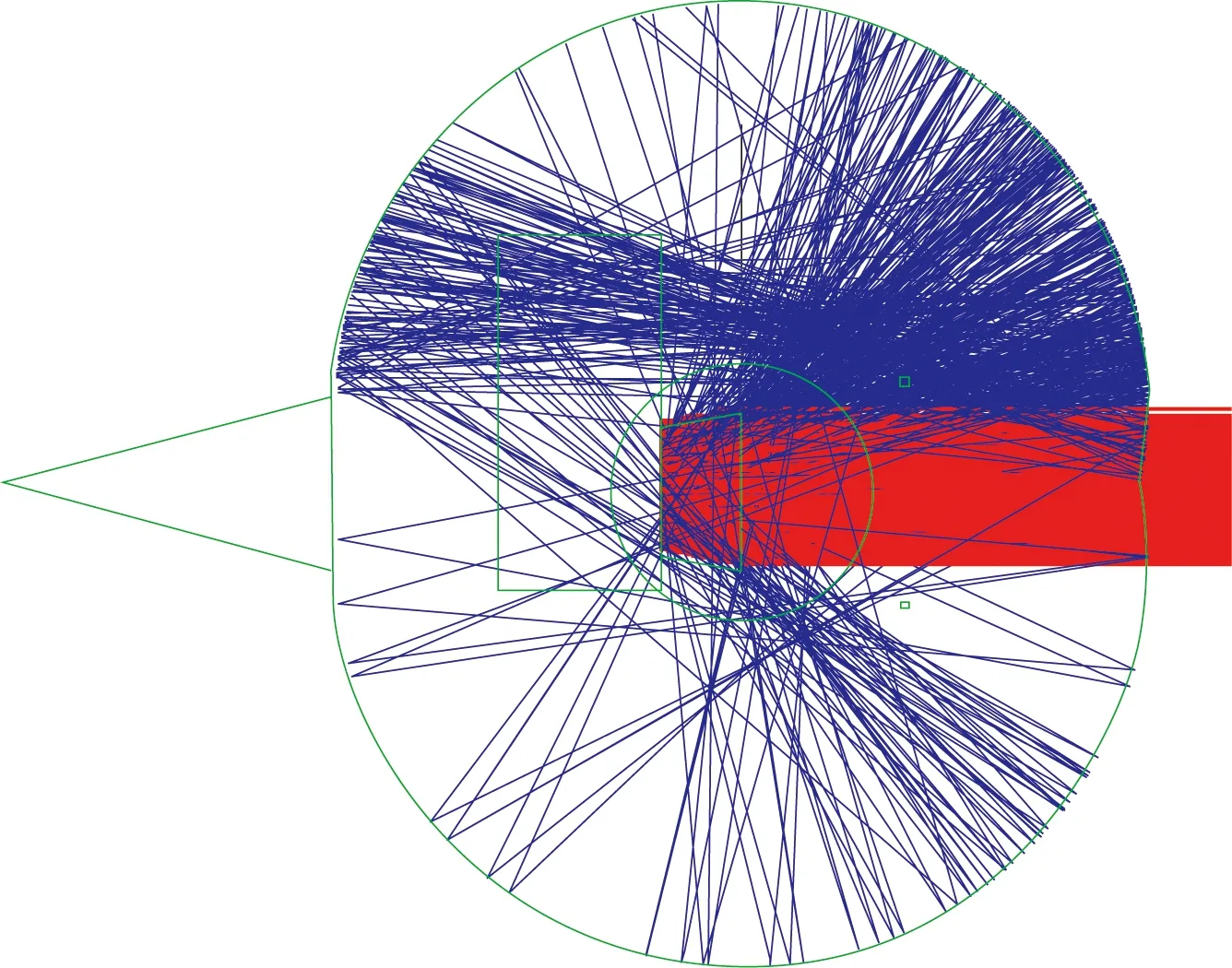
图15　双柱罐杂光分析示意图

另外，标准镜头PST的测试精度受空气灰尘散射的影响也较大。由于本次试验是在十万级环境中进行的，若将以后的工作环境改善至千级，将大大降低空气散射而产生的杂散光污染，从而有利于提高标准镜头的校准精度。

6　结　论

为了标定PST测试系统的测试精度，本文研究并设计了一种标准镜头，通过对标准镜头光学元件表面属性的计算以及结构件表面属性的测试和建模分析，利用Tracepro软件对标准镜头的PST理论值进行了分析计算，最后通过PST测试系统对标准镜头进行了测试。根据公式计算出标准镜头的测试精度，即得到该测试系统的校准误差。试验结果表明：该标准镜头的PST分析值与实测值之差优于lg/0.5，完全满足该测试系统的校准要求。这为国内PST测试系统的精度校准问题提供了技术保障。

另外，测试结果还表明点源透过率测试系统的测量精度受双柱罐及空气洁净度的影响较大。在以后的研究工作中，若改进双柱罐的设计，并提高环境空气的洁净度，PST测试精度有望提高至新的量级。

[1]李婷，杨建峰，阮萍，等.月基天文光学望远镜(LOT)的杂散光分析[J].光子学报，2007，36(增刊)：136-141.

LI T，YANG J F，RUAN P，etal.. Stray light analysis of the lunar-based optical telescope[J].ActaPhotonicaSinica，2007，36(Suppl.)：136-141.(in Chinese)

[2]杨林，李达，崔天刚，等.空间太阳望远镜在紫外波段成像检测中的杂散光测量和消除[J].光学 精密工程，2011，19(7)：1456-1463.

YANG L，LI D，CUI T G，etal.. Measurement and elimination of stray light from space solar telescopes for imaging test at UV band [J].Opt.PrecisionEng.，2011，19(7)：1456-1463.(in Chinese)

[3]徐亮，赵建科，薛勋，等.月基望远镜杂散光PST研究与测试[J].红外与激光工程，2014，43(4)：1289-1294.

XU L，ZHAO J K，XUE X，etal.. PST research and measurement of lunar-based optical telescope stray light[J].InfraredandLaserEngineering，2014，43(4)：1289-1294.(in Chinese)

[4]廖胜，沈忙作.红外光学系统杂光PST 的研究与测试[J].红外与毫米波学报，1996，15(5)：375-378.

LIAO SH，SHEN M Z. Point source transmittance of stray light of infrared optical systems and its measurements[J].J.InfraredMillim.Waves，1996，15(5)：375-378.(in Chinese)

[5]JOHN F，FRANK G，TIM F，etal.. New stray light test facility and initial results [J].SPIE，2008，7069：1-5.

[6]钟兴，贾继强.空间相机消杂光设计及仿真[J].光学 精密工程，2009，17(3)：621-625.

ZHONG X，JIA J Q. Stray light removing design and simulation of spaceborne camera[J].Opt.PrecisionEng.，2009，17(3)：621-625.(in Chinese)

[7]闫佩佩，樊学武.R-C光学系统设计及杂散光分析[J]. 红外技术，2011，33(4)：214-217.

YAN P P，FAN X W. Optical design and stray light analysis of R-C system[J].InfraredTechnology，2011，33(4)：214-217.(in Chinese)

[8]FRANK G，JOHN F. Stray light testing of the OLI telescope [J].SPIE，2010，7794：77940W-1-77940W-13.

[9]STEPHEN M P， RICHARD R P， JEFFREY M M. A stray light analysis of apache point observatory 3.5 meter telescope system [J].SPIE，2003，4842：128-138.

[10]ERIC C F.Stray light analysis and control [J].SPIE，2013，62-75.

[11]颜昌翔，许杰，彭岩.离轴三反空间光学望远系统的杂散光抑制[J].光学 精密工程，2010，18(2)：289-293.

YAN CH X，XU J，PENG Y. Stray light suppression of three-mirror off-axis space optical telescope [J].Opt.PrecisionEng.，2010，18(2)：289-293.(in Chinese)

[12]GARY L P. Stray light test station for measuring point source transmission and thermal background of visible and infrared sensors [J].SPIE，2008，7069： 70690M-1-70690M-9.

徐亮(1984-)，男，陕西西安人，博士研究生，工程师，2006年于西安工业大学获得学士学位，2009年于长春理工大学获得硕士学位，主要从事光学设计与弱光测试技术的研究。E-mail：xuliang757@163.com

导师简介：

高立民(1965-)，男，陕西西安人，博士，研究员，博士生导师，1991年、2004年于西安光机所分别获得硕士、博士学位，主要从事光学工程领域的研究。E-mail：glm@opt.ac.cn

(本栏目编辑：曹金)

(版权所有未经许可不得转载)

Calibration of stray light based on point source transmittance measurement system

XU Liang1，2*， GAO Li-min1， ZHAO Jian-ke1， LIU Feng1，ZHOU Yan1， LI Zhao-hui1，2， YANG Fei3， ZHAO Qing1，2

(1.Xi′anInstituteofOpticsandPrecisionMechanics，ChineseAcademyofSciences，Xi′an710119，China；2.UniversityofChineseAcademyofSciences,Beijing100049,China；3.AVICXi′anAircraftIndustry(Group)CompanyLTD.，Xi′an710089，China)

*Correspondingauthor，E-mail：xuliang757@163.com

To improve the stray light testing ability and calibration accuracy of the stray light equipment used in test of the Point Source Transmittance (PST), a calibration lens was proposed to calibrate the testing range and testing accuracy of the equipment in a large off-axial angle. By using a simple physical model, the calibration lens was designed in a laboratory. The physical parameters of the calibration lens were measured, then these parameters were taken into the TracePro to calculate the PSTs in different off-axial angles. Finally, the calculated result and the tested result of PSTs were compared, and the test accuracy of the equipment were obtained. The experimental results indicate that the difference between calculate results and testing results of the calibration lens is better than lg/0.5, meeting the need of testing accuracy calibration of the stray light equipment in testing PSTs and providing a reliable reference for the absolute measurement of PSTs. This technology solves the problem in testing accuracy calibration of PST measuring systems.

point source transmittance measurement；stray light measurement；standard lens; calibration； bidirectional reflectance distribution function

2016-03-02；

2016-04-11.

国防科工局专项资金资助项目

1004-924X(2016)07-1607-08

TH703； TH743

Adoi:10.3788/OPE.20162407.1607