系统辨识在水位流量关系中的应用分析

杨毅

（长沙市水文局 湖南长沙 410000）

系统辨识在水位流量关系中的应用分析

杨毅

（长沙市水文局 湖南长沙 410000）

需要使用传统方法拟合平稳河流的水位流量的关系，但是其精确度不高，于实际测量差异较大。就局部的线性水位流量关系来说，可以使用系统辨识理论根据实际情况建模，采用最小二乘法，实践发现精确度明显提高。本文就系统辨识在水位流量关系中的应用进行分析，供相关人士参考。

系统辨识；水位流量；最小二乘法；应用

1 引言

在水文学中，水文资料整编是水文资料收集和资料的具体应用的关键所在。在水文资料中，流量资料是较为重要的资料之一，流量资料整编时需要确定水位流量的关系。当前，对于水位流量关系的处理，以往是采用曼宁公式。但是因为计算误差较大，所以现多使用系统辨识方法对稳定河道水位流量关系的确立进行深入分析。可以在差分方程的系统辨识反馈算法依据环境的实际情况对系统模型参数进行调整。

2 流量与水位关系

流量水位关系指的是河渠中某断面的流量与其水位之间的对应状态，它是由各种水力因素，如水面宽、断面面积、水力比降、糙率等决定的。在较长时期内，河渠具备下列条件之一，则认为流量与水位关系是稳定的：①断面面积、水力比将以及糙率等多种水力因素均处于同一水位时，各项参数不会发生变化；②当处于同一水位时，上述因素虽然有部分发生变化，但是其变化不会对水位流量关系造成太大影响，其可以通过相互补偿抵消。基于此种情况，同一水位只有一个相应流量，即给定一个流量可以唯一地确定与之对应的水位。然而，实际上受一种或几种因素的影响，流量与水位的关系不会是理想的稳定状态，即给定一个流量值并不能唯一地确定与之对应的水位，同一流量具有多个水位与之对应，同一流量下对应的水位虽大致相近，但是也存在一定的差值。

可以对水位流量关系造成影响且影响后会发生变化的因素主要如下：①河床冲淤，使得同一水位的断面面积会发生较大变化，并影响流量，多沙的河流冲淤也会比较严重，变化较大；②洪水会发生涨落，在涨水和落水过程中，河道水面的比降也有所差异，流速不同也会造成同一水位下流量的不同，涨落较大的河流，此类变化会比较显著；③变动回水，在河流的中下游，河渠水位受到支流汇合、闸门启动和关闭、湖水顶托等多种影响，使得水面比降发生变化，造成水位流量关系不稳定；④结冰、水生植物等也会导致断面面积以及糙率等水力因素发生变化，造成流量水位关系出现变动。

在各种水力因素资料有限，且影响流量与水位关系稳定性的因素不确定的状态下，可考虑采用统计学的方法，通过对站点历史水位与流量资料的分析，确定流量与水位的关系。

3 系统辨识在数位流量关系确立中的应用

3.1 模型建立

如果高程H步长相同，流量Q会随着H的增大而逐渐趋于稳定，可为被识别系统建模型；H为输入序列u，Q为输出序列y，系统是单输入单输出的线性系统结构参数的确定被视为模型阶以及纯滞后时间的估测。模型形式如下：

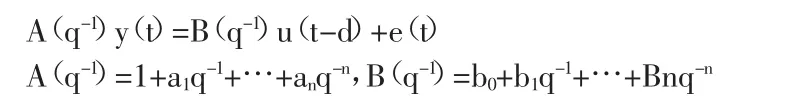
式中：n-模型阶次；d-时滞。在水位流量关系模型中，d=0。

3.2 模型阶的估计

在水位流量关系中，可以采用以下的模型阶估计方法。

3.2.1 零-极相消检验

任给阶次为n的估计模型：

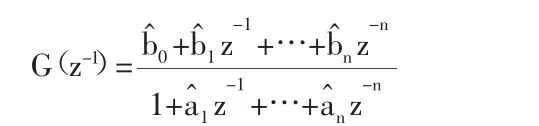
式中：n0-系统的真实阶次，如果n＞n0，则零-极相互抵消。将分子分母上大致相同根的因子抵消后，分子多项式或者分母多项式的次数都可以作为模型阶估测的主要依据。

3.2.2 残差统计特性检验

考虑差分方程模型：y（t）=φ（Tt-1）θ+ξ（t）式中：φ（Tt）-输入/输出观测向量；θ-参数向量；{ξ（t）}-白噪声序列。

某模型阶ni对应有参数估计θi，则输出的实测值和预测值之间的差异，也就是模型残差：

3.2.3 F检验法

取预报误差准则函数如下：

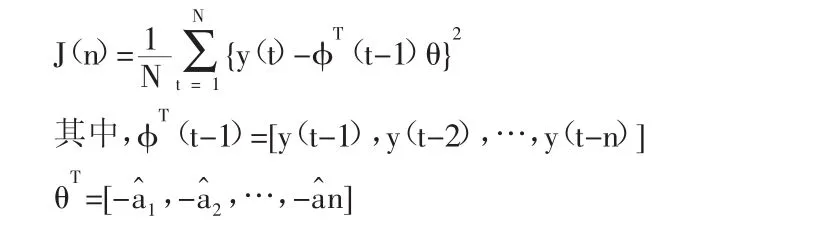
随着模型阶次和真实值的差距越来越小，准则函数不断减小。当准则函数没有发生较为明显的变化时，可以将此时n作为模型阶的估计参考值。

3.2.4 赤迟检验法

在应用赤迟检验法的时候，可以采用Yule-walker估计法，求得y（t）的自相关函数：

所以可以得到参数估计

N充分大时方差σ2的估计为

赤池提出了检验模型阶的基本原则，最终预报误差准则即FPE为：

对上述四种方法进行比较，第一种方法和第二种方法的人为操作成分较多，第三种方法确定的阶次容易较高，且具有很高的不确定性。对四种方法进行比较发现赤迟法的理论含义更加明确，弥补了前几种的方法的不足之处，在局部线性的水位流量模型中可以作为定阶的方法使用。

3.3 模型参数的辨识

设定噪声为MA序列，根据上述公式根据得出被识别系统模型为：

ξ（t）实际上是在递推过程中通过估计式计算得出。递推算法实际上是一种实时处理方法，其存储以及计算量都比较小，在采集了新的数据之后，可以不用对所有数据进行计算，只需要根据新提供的信息数据对照原有的估计量进行修正。增广矩阵法基于辨识的最小二乘法原理得出，其递推公式如下：

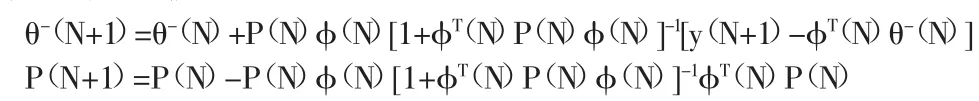
4 结束语

综上所述，采用系统辨识方法将差分方程作为数学模型，系统此刻输出完全都是由前一段时间的输入、输出以及此刻输入共同决定的。从物理角度来说，需要对河道的水位流量关系进行处理时，需要将河道的此刻流量作为河道前一刻的流量以及此刻输入水位的加权和（一阶时）。因为河道中的水流是不断变化的，其前后会相互影响，河道此刻的流量和前一时刻的流量也有着一定的关联。因此，输入在一定程度上表明了河道新输入的流量以及变化，所以可以使用系统辨识的方法对河道的水位流量关系进行处理，并且明确其物理意义。另外，由于河道的前一时刻的输出中已经包括了诸多不稳定的影响因素，作为需要将其作为输入的一部分表明输出，其会抵消不确定因素的影响。总之，可以使用系统辨识的方法处理稳定河道水位流量关系，明确具体的物理意义，可以保证拟合精度。

[1]施文军.渠系水位流量关系率定系统在玛纳斯河灌区的应用与分析[J].水利科技与经济，2012，18（6）：25～26.

[2]邹宁，徐松涛，任国磊.改进SVSLMS算法在系统辨识中的应用及性能分析[J].计算机工程与应用，2011，47（10）：229～232.

[3]李厚永，张潮，吴琼.水位流量关系单值化分析综合模型研究及应用[J].水文，2011（S1）：152～153.

[4]张尚弘，易雨君，陈稚聪，等.重庆河段水沙分析系统的开发与应用[J].水力发电学报，2012，31（01）：178～182.

TP391.4

A

1004-7344（2016）24-0152-02

2016-8-9

杨毅（1966-），男，助理工程师，主要从事水文勘测工作。